A Hybrid Model of VAR-DCC-GARCH and Wavelet Analysis for Forecasting Volatility †
Abstract
:1. Introduction
- It shows whether a conditional correlation exists in the weekly exchange rate, gold, and stock market returns by using DCC-GARCH and VAR-DCC-GARCH.
- It reveals that performance of VAR-DCC-GARCH model is better than that of DCC-GARCH model using out-of-sample prediction by WRF.
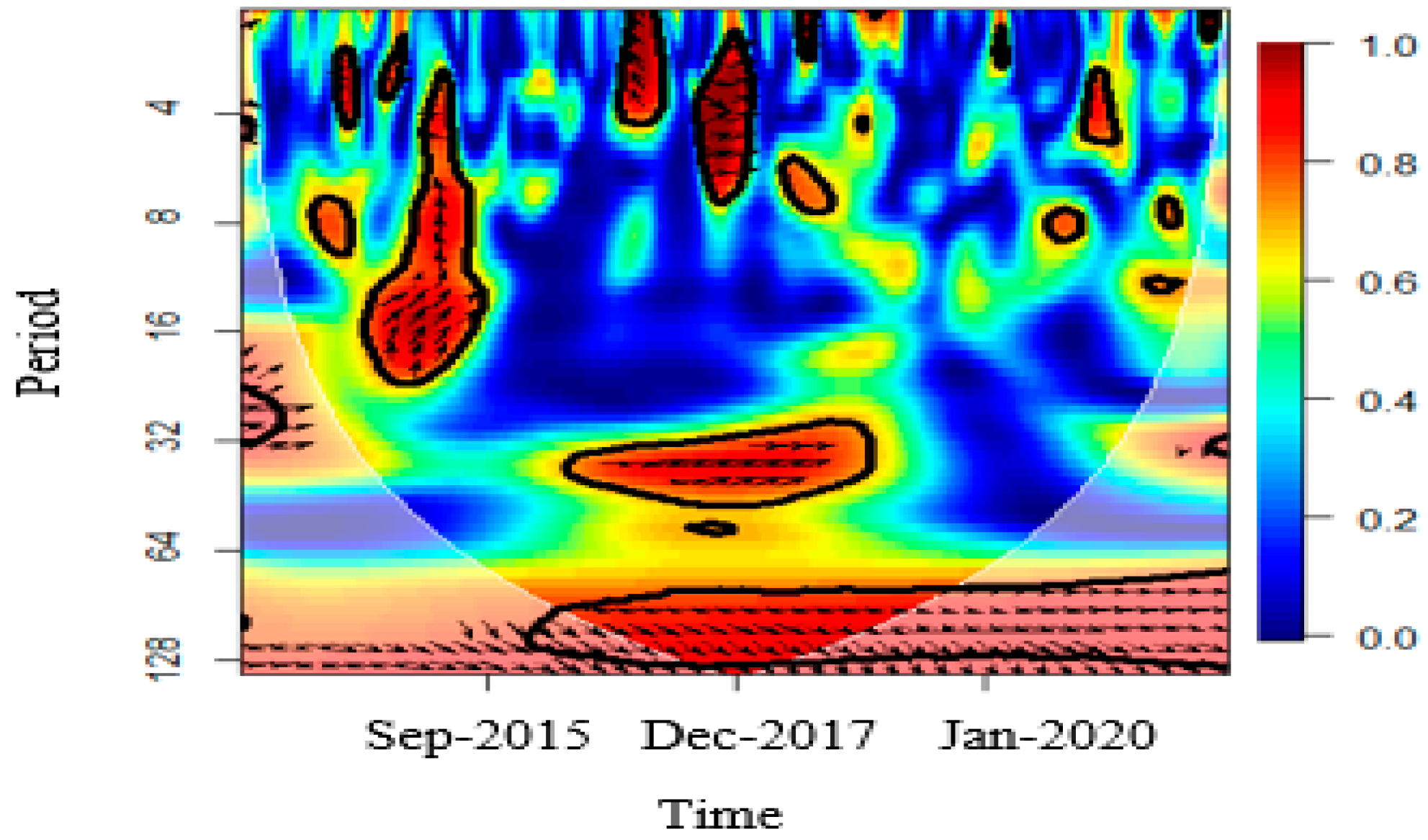
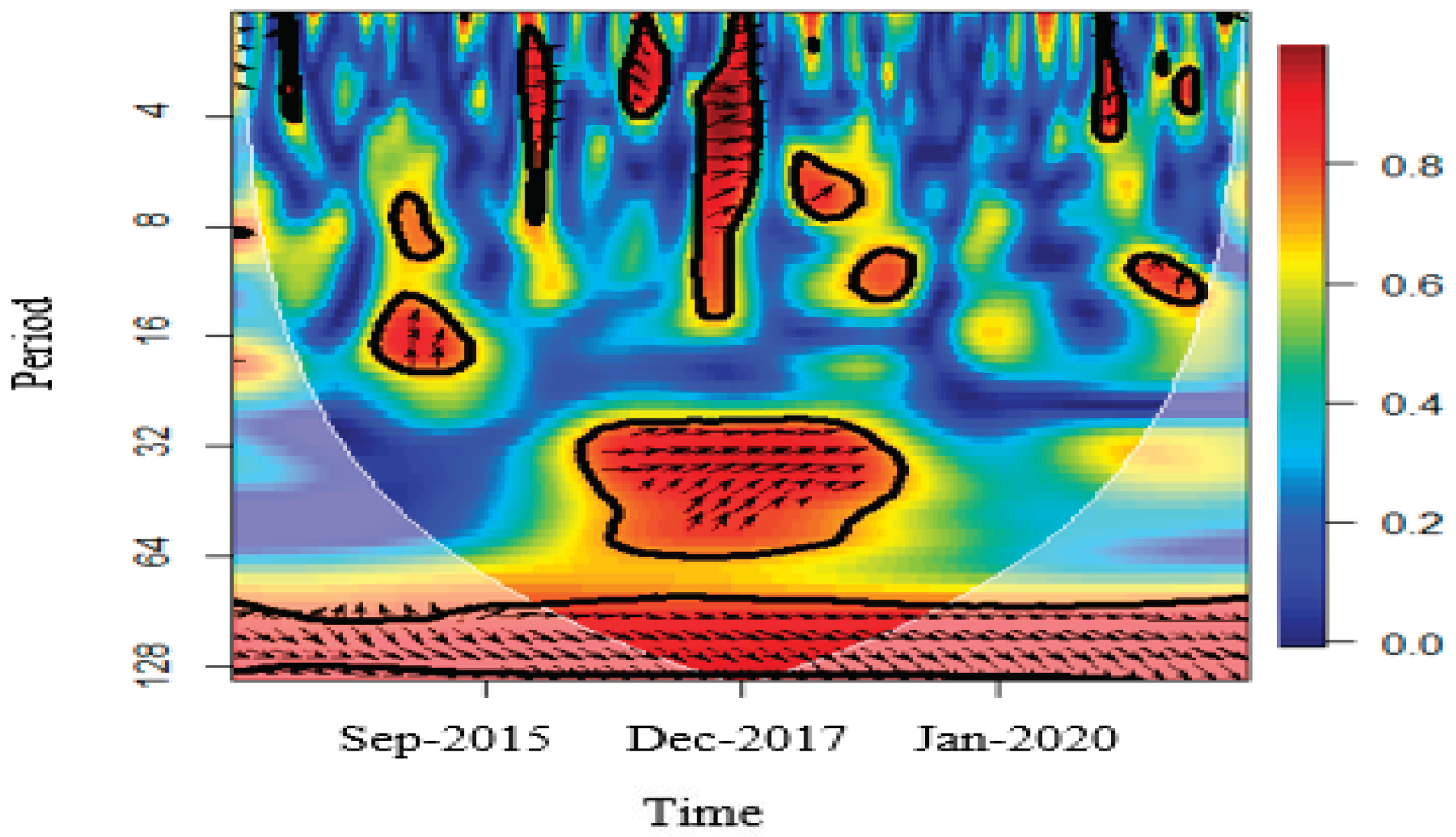
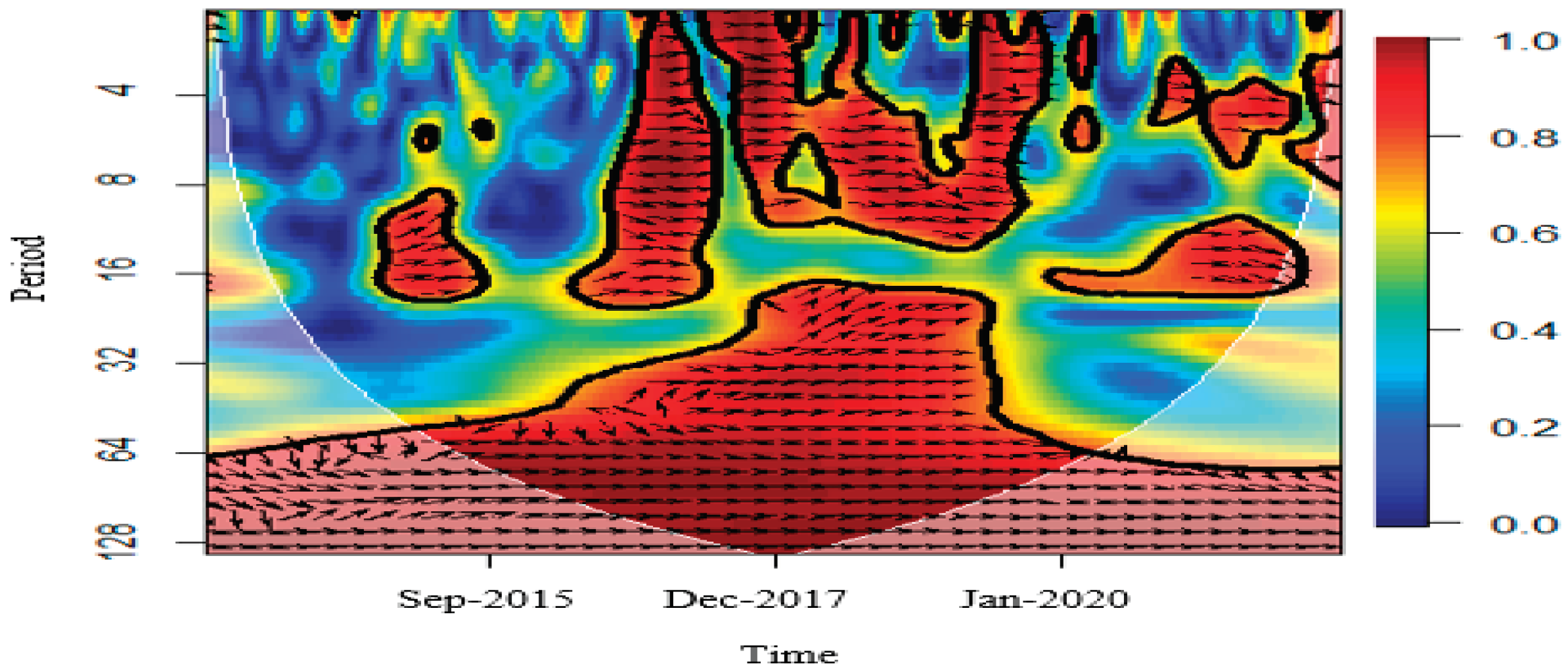
- It identifies the time-varying nature of the correlation among the Iranian financial market’s volatilities indexes using CWT.
- This study helps investors identify the optimal portfolio by identifying asset-return volatility and portfolio diversification.
2. Materials and Methods
2.1. VAR-DCC-GARCH
2.2. Wavelet-Based Random Forest
2.3. Continuous Wavelet Analysis
3. Discussion
3.1. Forecasting Performance
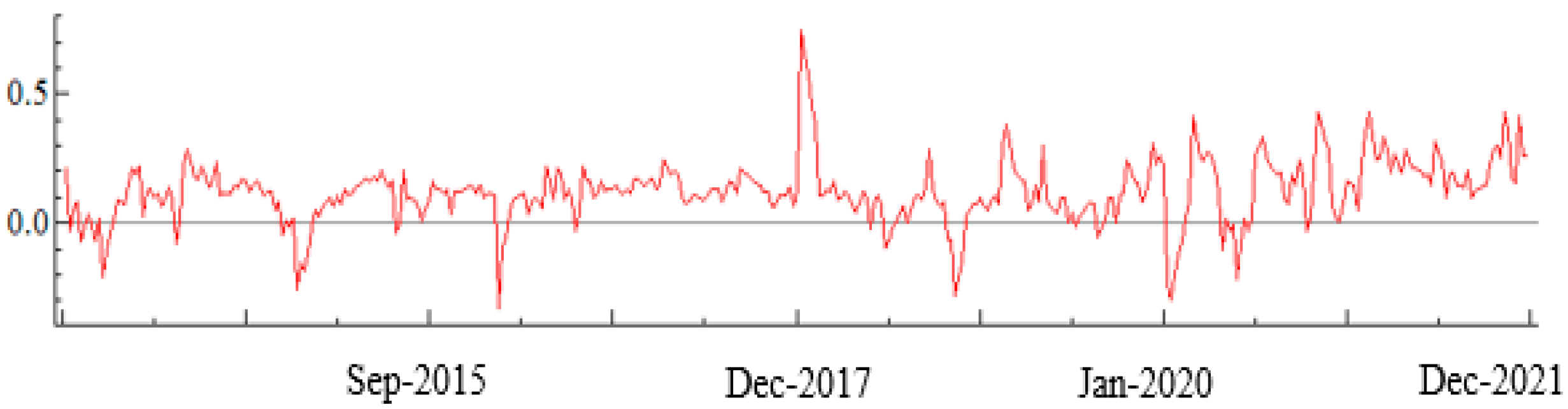
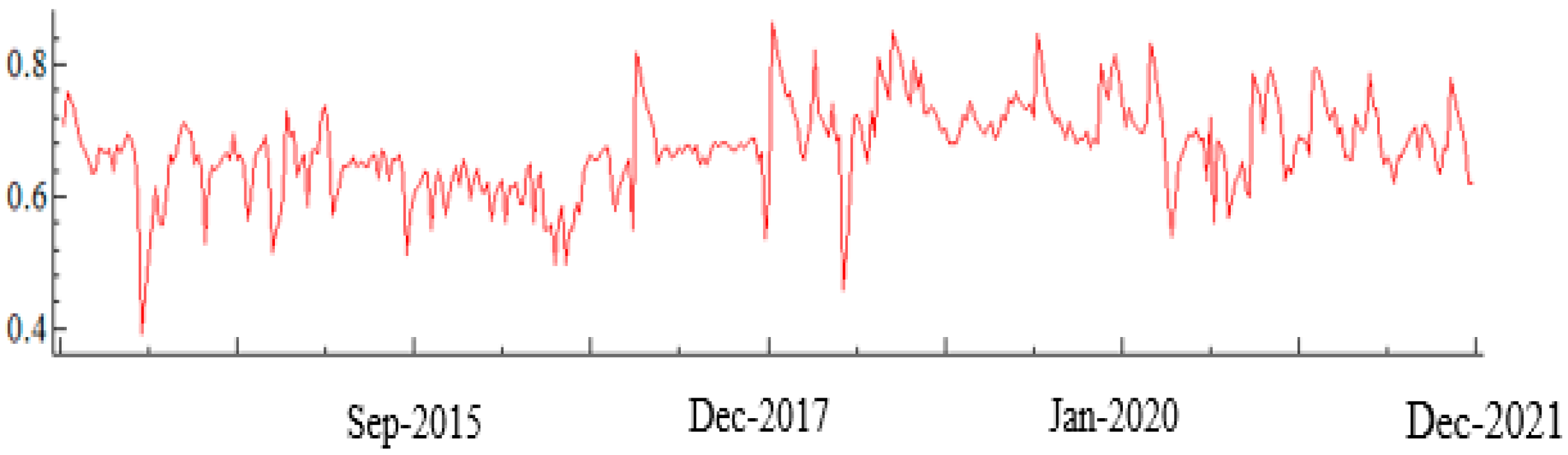
3.2. Results of Wavelet Coherence Estimation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ping, P.Y.; Ahmad, M.H.; Ismail, N. Analysis of Volatility Spillover Effects Using Trivariate GARCH Model. Rep. Econ. Financ. 2016, 2, 61–68. [Google Scholar] [CrossRef]
- Koo, E.; Kim, G. A Hybrid Prediction Model Integrating GARCH Models with a Distribution Manipulation Strategy Based on LSTM Networks for Stock Market Volatility. IEEE Access 2022, 10, 34743–34754. [Google Scholar] [CrossRef]
- Dahir, A.M.; Mahat, F.; Ab Razak, N.H.; Bany-Ariffin, A.N. Revisiting the dynamic relationship between exchange rates and stock prices in BRICS countries: A wavelet analysis. Borsa Istanb. Rev. 2018, 18, 101–113. [Google Scholar] [CrossRef]
- Bodnar, G.M.; Gentry, W.M. Exchange rate exposure and industry characteristics: Evidence from Canada, Japan, and the USA. J. Int. Money Financ. 1993, 12, 29–45. [Google Scholar] [CrossRef]
- Aggarwal, R. Exchange rates and stock prices: A study of the United States capital markets under floating exchange rates. Akron Bus. Econ. Rev. 1981, 12, 7–12. [Google Scholar]
- Kim, K. Dollar exchange rate and stock price: Evidence from multivariate cointegration and error correction model. Rev. Financ. Econ. 2003, 12, 301–313. [Google Scholar] [CrossRef]
- Doong, S.C.; Yang, S.Y.; Wang, A.T. The dynamic relationship and pricing of stocks and exchange rates: Empirical evidence from Asian emerging markets. Acad. Bus. J. 2005, 7, 118–123. [Google Scholar]
- Erdogan, S.; Gedikli, A.; Cevik, E.İ. Volatility spillover effects between Islamic stock markets and exchange rates: Evidence from three emerging countries. Borsa Istanb. Rev. 2020, 20, 322–333. [Google Scholar] [CrossRef]
- Gavin, M. The stock market and exchange rate dynamics. J. Int. Money Financ. 1989, 8, 181–200. [Google Scholar] [CrossRef] [Green Version]
- Zhao, H. Dynamic relationship between exchange rate and stock price: Evidence from China. Res. Int. Bus. Financ. 2010, 24, 103–112. [Google Scholar] [CrossRef]
- Hashim, K.K.; Masih, M. Stock Market Volatility and Exchange Rates: MGARCH-DCC and Wavelet Approaches; MPRA Paper No. 65234; MPRA: Munich, Germany, 2015. [Google Scholar]
- Gilmore, C.G.; McManus, G.M.; Sharma, R.; Tezel, A. The dynamics of gold prices, gold mining stock prices and stock market prices comovements. Res. Appl. Econ. 2009, 1, 1–19. [Google Scholar] [CrossRef]
- Mishra, P.K.; Das, J.R.; Mishra, S.K. Gold price volatility and stock market returns in India. Am. J. Sci. Res. 2010, 9, 47–55. [Google Scholar]
- Srinivasan, P.; Karthigai, P. Gold Price, Stock Price and Exchange Rate Nexus: The Case of India. IUP J. Financ. Risk Manag. 2014, 11, 1–12. [Google Scholar]
- Arouri, M.E.H.; Lahiani, A.; Nguyen, D.K. World gold prices and stock returns in China: Insights for hedging and diversification strategies. Econ. Model. 2015, 44, 273–282. [Google Scholar] [CrossRef] [Green Version]
- Jain, A.; Biswal, P.C. Dynamic linkages among oil price, gold price, exchange rate, and stock market in India. Resour. Policy 2016, 49, 179–185. [Google Scholar] [CrossRef]
- Yousaf, I.; Ali, S. Linkages between gold and emerging Asian stock markets: New evidence from the Chinese stock market crash. Stud. Appl. Econ. 2021, 39, 26. [Google Scholar] [CrossRef]
- Sjaastad, L.A. The price of gold and the exchange rates: Once again. Resour. Policy 2008, 33, 118–124. [Google Scholar] [CrossRef]
- Qureshi, S.; Rehman, I.U.; Qureshi, F. Does gold act as a safe haven against exchange rate fluctuations? The case of Pakistan rupee. J. Policy Model. 2018, 40, 685–708. [Google Scholar] [CrossRef]
- Wang, K.M.; Thi, T.B.N.; Lee, Y.M. Is gold a safe haven for the dynamic risk of foreign exchange? Future Bus. J. 2021, 7, 56. [Google Scholar] [CrossRef]
- Engle, R. Dynamic conditional correlation: A simple class of multivariate generalized autoregressive conditional heteroskedasticity models. J. Bus. Econ. Stat. 2002, 20, 339–350. [Google Scholar] [CrossRef]
- Tse, Y.K.; Tsui, A.K.C. A multivariate generalized autoregressive conditional heteroscedasticity model with time-varying correlations. J. Bus. Econ. Stat. 2002, 20, 351–362. [Google Scholar] [CrossRef]
- Prieto, C.; Le Vine, N.; Kavetski, D.; García, E.; Medina, R. Flow prediction in ungauged catchments using probabilistic random forests regionalization and new statistical adequacy tests. Water Resour. Res. 2019, 55, 4364–4392. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Chapman and Hall/CRC: Boca Raton, FL, USA, 1984. [Google Scholar]
- Woznicki, S.A.; Baynes, J.; Panlasigui, S.; Mehaffey, M.; Neale, A. Development of a spatially complete floodplain map of the conterminous United States using random forest. Sci. Total Environ. 2019, 647, 942–953. [Google Scholar] [CrossRef]

| TEPIX | USD | Gold | |
|---|---|---|---|
| Mean | 0.87 | 0.5507 | 0.636 |
| Maximum | 15.71 | 16.80 | 15.88 |
| Minimum | −10.74 | −10.87 | −11.71 |
| Sd | 3.29 | 2.96 | 3.12 |
| skewness | 0.91 | 1.28 | 0.85 |
| kurtosis | 6.51 | 10.22 | 7.59 |
| Jb | 260.08 | 976.08 | 399.15 |
| Gold | Dollar | TEPIX | |
|---|---|---|---|
| gold | 1 | ||
| USD | 0.777 | 1 | |
| TEPIX | 0.1899 | 0.1552 | 1 |
| Akaike | Bayes | Hannan-Quinn | |
|---|---|---|---|
| 1 | 13.045 | 13.305 | 13.148 |
| 2 | 13.092 | 13.442 | 13.231 |
| 3 | 13.151 | 13.591 | 13.325 |
| Coefficient | p-Value | ||
|---|---|---|---|
| TEPIX | 0.327 | 0.02 | |
| 0.5058 | 0.000 | ||
| 0.087 | 0.24 | ||
| −0.005 | 0.94 | ||
| USD | 0.362 | 0.000 | |
| 0.0678 | 0.000 | ||
| −0.0591 | 0.000 | ||
| 0.2856 | 0.000 | ||
| gold | 0.470 | 0.003 | |
| 0.1376 | 0.004 | ||
| −0.097 | 0.23 | ||
| 0.1924 | 0.01 |
| VAR-DCC-GARCH | DCC-GARCH | ||||
|---|---|---|---|---|---|
| Coefficient | p-Value | ||||
| TEPIX | 0.358 | 0.21 | 1.07 | 0.14 | |
| 0.1399 | 0.05 | 0.29 | 0.03 | ||
| 0.808 | 0.000 | 0.527 | 0.01 | ||
| USD | 0.47 | 0.11 | 0.47 | 0.18 | |
| 0.216 | 0.003 | 0.44 | 0.05 | ||
| 0.719 | 0.000 | 0.56 | 0.000 | ||
| gold | 0.1599 | 0.08 | 0209 | 0.05 | |
| 0.1703 | 0.001 | 0.309 | 0.001 | ||
| 0.8234 | 0.000 | 0.689 | 0.000 | ||
| DCC | 0.095 | 0.006 | 0.028 | 0.02 | |
| 0.639 | 0.02 | 0.956 | 0.000 | ||
| VAR-DCC-GARCH | DCC-GARCH | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| MSE | RMSE | R-Sq | MAE | MSE | RMSE | R-Sq | MAE | ||
| USD | Train | 19.40 | 4.4 | 0.93 | 1.8 | 66.85 | 8.17 | 0.88 | 3.2 |
| Test | 3.4 | 1.8 | 0.98 | 1.16 | 13.03 | 3.6 | 0.97 | 2.11 | |
| gold | Train | 10.5 | 3.2 | 0.97 | 1.62 | 28.61 | 5.35 | 0.93 | 2.44 |
| Test | 3.5 | 1.87 | 0.98 | 1.21 | 9.46 | 3.07 | 0.97 | 1.96 | |
| TEPIX | Train | 3.47 | 1.86 | 0.89 | 0.96 | 22.52 | 4.74 | 0.86 | 2.20 |
| Test | 13.27 | 3.64 | 0.95 | 2.27 | 50.7 | 7.07 | 0.94 | 3.96 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nafisi-Moghadam, M.; Fattahi, S. A Hybrid Model of VAR-DCC-GARCH and Wavelet Analysis for Forecasting Volatility. Eng. Proc. 2022, 18, 6. https://doi.org/10.3390/engproc2022018006
Nafisi-Moghadam M, Fattahi S. A Hybrid Model of VAR-DCC-GARCH and Wavelet Analysis for Forecasting Volatility. Engineering Proceedings. 2022; 18(1):6. https://doi.org/10.3390/engproc2022018006
Chicago/Turabian StyleNafisi-Moghadam, Maryam, and Shahram Fattahi. 2022. "A Hybrid Model of VAR-DCC-GARCH and Wavelet Analysis for Forecasting Volatility" Engineering Proceedings 18, no. 1: 6. https://doi.org/10.3390/engproc2022018006
APA StyleNafisi-Moghadam, M., & Fattahi, S. (2022). A Hybrid Model of VAR-DCC-GARCH and Wavelet Analysis for Forecasting Volatility. Engineering Proceedings, 18(1), 6. https://doi.org/10.3390/engproc2022018006






