Numerical Prediction of the Influence of Process Parameters and Process Set-Up on Damage Evolution during Deep Drawing of Rectangular Cups †
Abstract
1. Introduction
1.1. Initial Situation
Definition of Damage
“The process of ductile damage describes the formation, growth and coalescence of voids in the microstructure. These voids are formed in structural materials by decohesion at interfaces such as phase/grain boundaries and inclusions, or by the formation of new surfaces within phases or inclusions. This damage causes degradation of the performance of the corresponding component.”
1.2. State of the Art
1.2.1. Damage Modelling
1.2.2. Deep Drawing
1.2.3. Damage Evolution during Deep Drawing
2. Materials and Methods
2.1. Deep Drawing Process
2.2. Process Model
3. Results
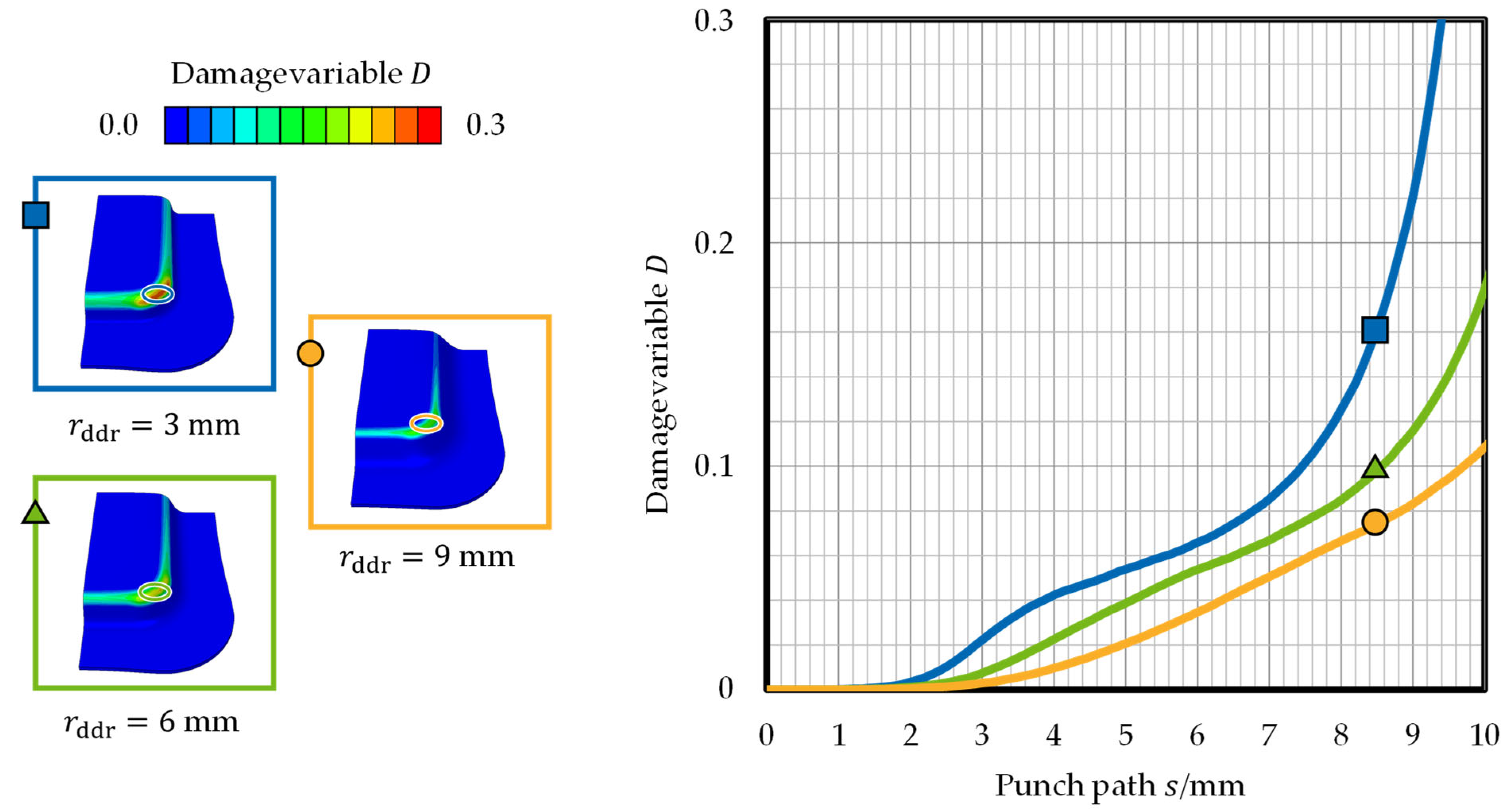
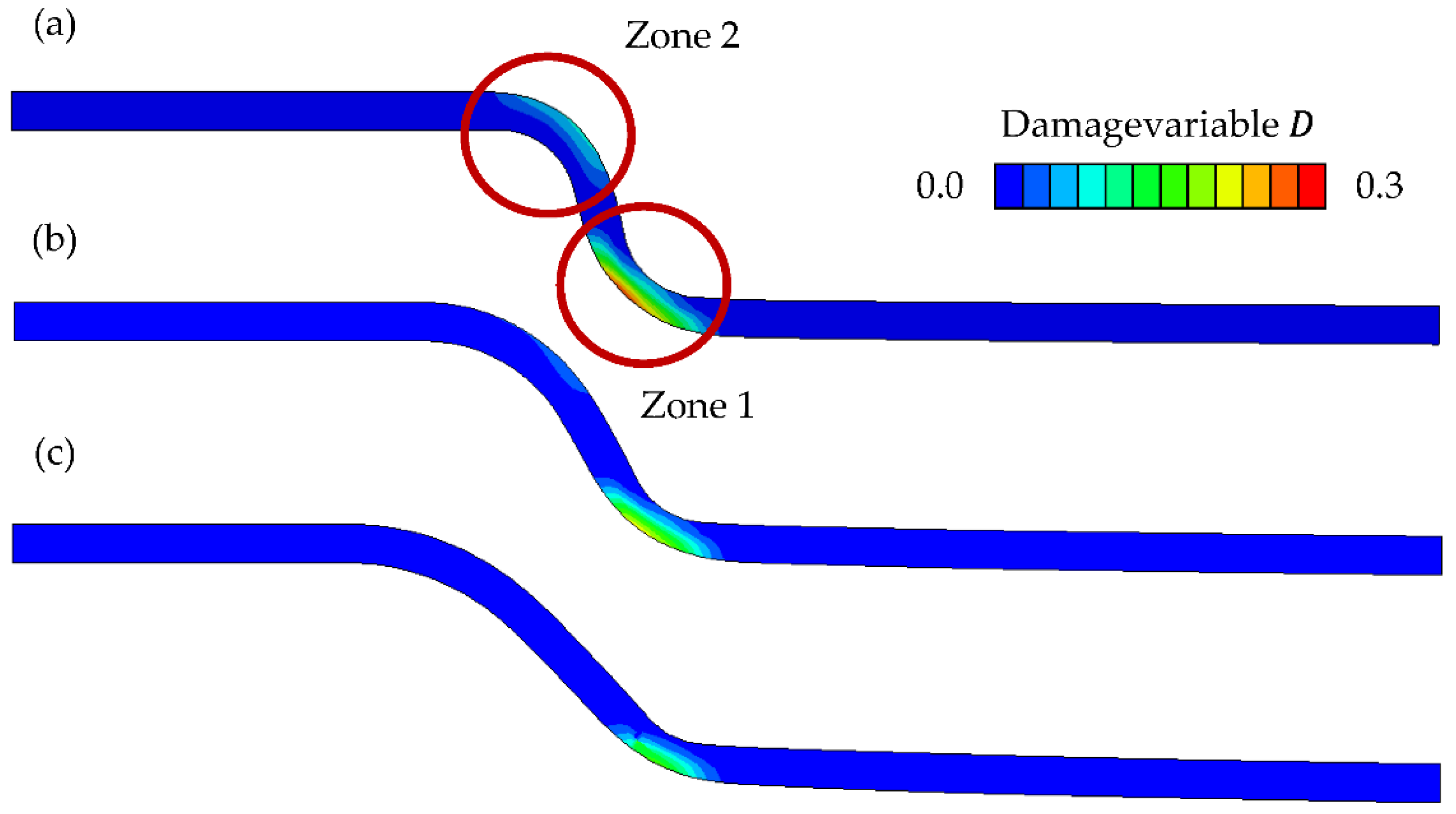
3.1. Influence of Process Parameter on Damage Evolution
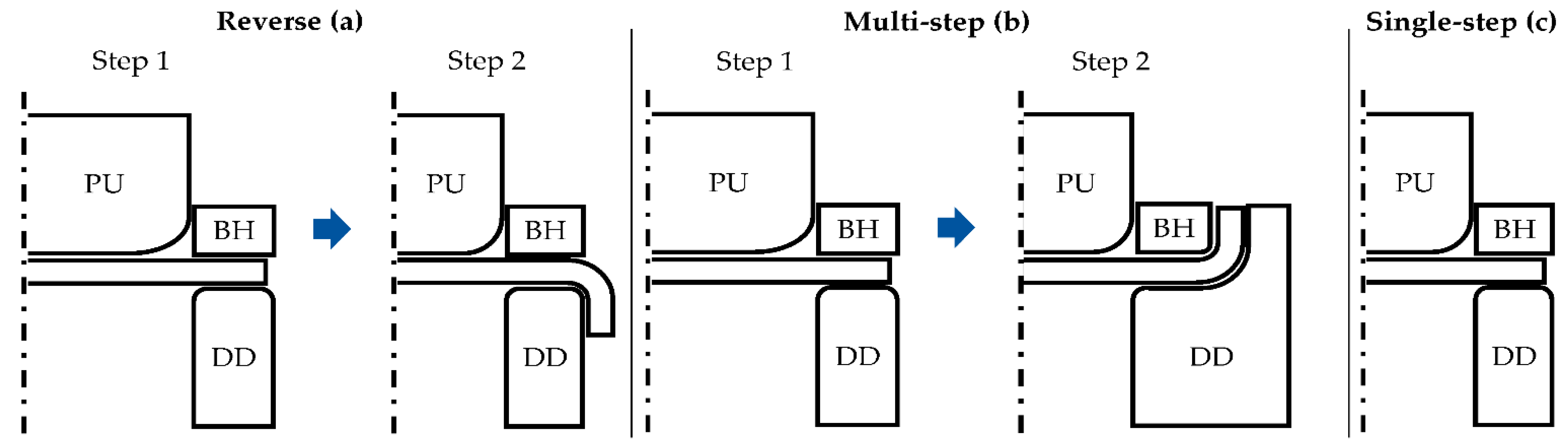
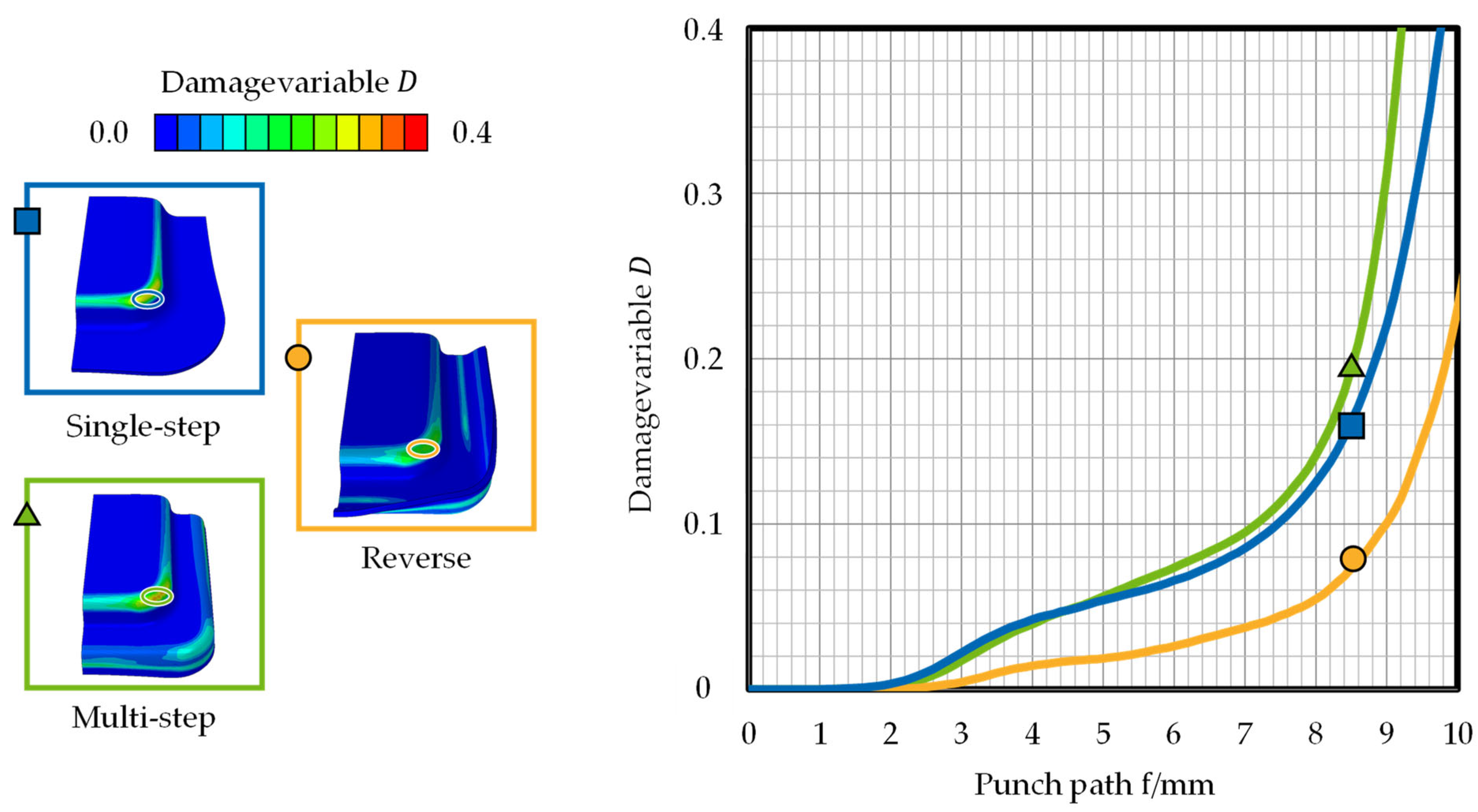
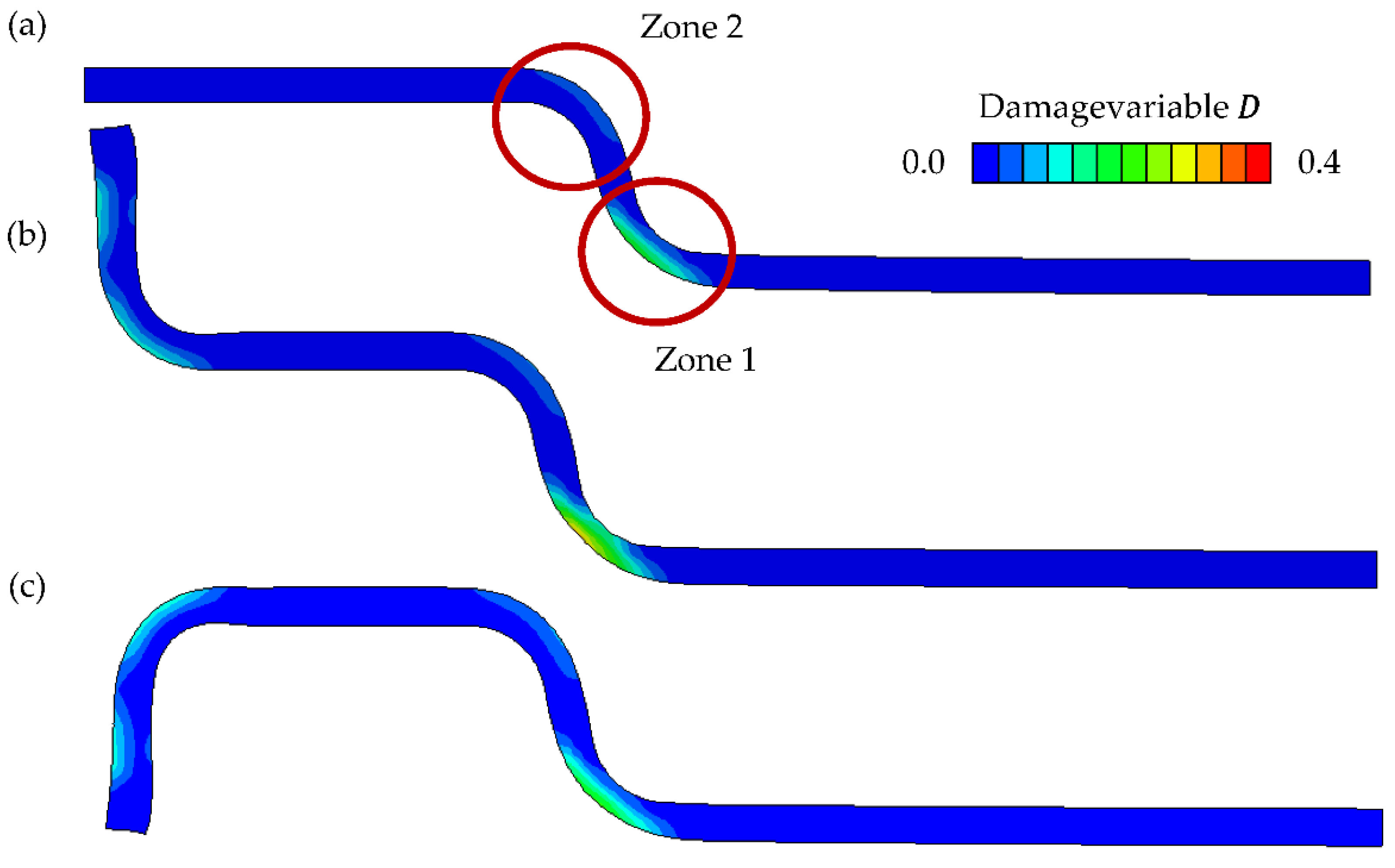
3.2. Influence of Process Set-Up on Damage Evolution
4. Discussion
4.1. Influence of Process Parameter on Damage Evolution
4.2. Influence of Process Set-Up on Damage Evolution
5. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- National or EU-Wide Inclusion of Further Sectors in the European Emissions Trading Scheme; Scientific Services of the German Federal Parliament: Berlin, Germany, 2018.
- European Commission. A European Green Deal; European Commission: Brussels, Belgium, 2019. [Google Scholar]
- Kim, H.J.; McMillan, C.; Keoleian, G.A.; Skerlos, S.J. Greenhouse Gas Emissions Payback for Lightweighted Vehicles Using Aluminum and High-Strength Steel. J. Ind. Ecol. 2010, 14, 929–946. [Google Scholar] [CrossRef]
- Birat, J.P. Life-cycle assessment, resource efficiency and recycling. Metall. Res. Technol. 2015, 112, 206–212. [Google Scholar] [CrossRef]
- Klocke, F. Manufacturing Processes 4. Forming, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Hirt, G.; Tekkaya, E.; Clausmeyer, T.; Lohmar, J. Potential and status of damage controlled forming processes. Prod. Eng. 2020, 14, 1–4. [Google Scholar] [CrossRef]
- Nick, M.; Liebsch, C.; Müller, M.; Weiser, I.F.; Hirt, G.; Bergs, T. Influence of pass reduction in cold rolling on damage evolution in deep drawing of rotationally symmetric cups. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1157, 012050. [Google Scholar] [CrossRef]
- Besson, J.J. Continuum Models of Ductile Fracture: A Review. Int. J. Damage Mech. 2010, 19, 3–52. [Google Scholar] [CrossRef]
- Tasan, C.; Hoefnagels, J.; Geers, M. Identification of the continuum damage parameter: An experimental challenge in modeling damage evolution. Acta Mater. 2012, 60, 3581–3589. [Google Scholar] [CrossRef]
- Cockcroft, M.G.; Latham, D. A Simple Criterion of Fracture for Ductile Metals; National Engineering Laboratory: East Kilbride, UK, 1966. [Google Scholar]
- Wierzbicki, T.; Bao, Y.; Lee, Y.W.; Bai, Y. Calibration and evaluation of seven fracture models. Int. J. Mech. Sci. 2005, 47, 719–743. [Google Scholar] [CrossRef]
- Gurson, A.L. Continuum Theory of Ductile Rupture by Void Nucleation and Growth: Part I—Yield Criteria and Flow Rules for Porous Ductile Media. J. Eng. Mater. Technol. 1977, 99, 2–15. [Google Scholar] [CrossRef]
- Needleman, A.; Tvergaard, V. An analysis of ductile rupture modes at a crack tip. J. Mech. Phys. Solids 1987, 35, 151–183. [Google Scholar] [CrossRef]
- Lemaitre, J. A Continuous Damage Mechanics Model for Ductile Fracture. J. Eng. Mater. Technol. 1985, 107, 83–89. [Google Scholar] [CrossRef]
- Lian, J.; Feng, Y.; Münstermann, S. A Modified Lemaitre Damage Model Phenomenologically Accounting for the Lode Angle Effect on Ductile Fracture. Procedia Mater. Sci. 2014, 3, 1841–1847. [Google Scholar] [CrossRef]
- Kachanov, L.M. Introduction to Continuum Damage Mechanics, 1st ed.; Springer: Dordrecht, The Netherlands, 1986. [Google Scholar]
- Soner, M. Schädigungsmechanische Charakterisierung Kunststoffvergossener Bauteile; RWTH-Aachen University: Aachen, Germany, 2004. [Google Scholar]
- Cao, T.S. Models for ductile damage and fracture prediction in cold bulk metal forming processes: A review. Int. J. Mater. Form. 2017, 10, 139–171. [Google Scholar] [CrossRef]
- Doege, E.; Behrens, B.A. Handbuch Umformtechnik. Grundlagen, Technologien, Maschinen, 3rd ed.; Springer Berlin Heidelberg: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Tiware, P.; Rathore, A.; Bodkhe, M. Factors affecting the deep drawing process. Mater. Today: Proc. 2022, 56, 2902–2908. [Google Scholar] [CrossRef]
- Dal, S.; Darendeliler, H. Analysis of Side-Wall Wrinkling in Deep Drawing Processes. Key Eng. Mater. 2022, 926, 732–743. [Google Scholar] [CrossRef]
- Chen, K.; Carter, A.; Korkolis, Y. Flange Wrinkling in Deep-Drawing: Experiments, Simulations and a Reduced-Order Model. J. Manuf. Mater. Process. 2022, 6, 76. [Google Scholar] [CrossRef]
- Preedawiphat, P.; Koowattanasuchat, N.; Mahayotsanun, N.; Mahabunphachai, S. Sheet thinning prediction method based on localized friction effect in deep-drawing. Adv. Mech. Eng. 2020, 12, 1–10. [Google Scholar] [CrossRef]
- Urmaz, U.; Heibel, S.; Schweiker, A.; Prabhakar, A.; Merklein, M. Influence of the forming process on springback. IOP Conf. Ser. Mater. Sci. Eng. 2022, 1238, 012074. [Google Scholar] [CrossRef]
- Nanu, N.; Brabie, G. Analytical model for prediction of springback parameters in the case of U stretch–bending process as a function of stresses distribution in the sheet thickness. Int. J. Mech. Sci. 2012, 64, 11–21. [Google Scholar] [CrossRef]
- Fan, J.; Tang, Y.; Tsui, C.; Chan, L.; Lee, T. 3D finite element simulation of deep drawing with damage development. Int. J. Mach. Tools Manuf. 2006, 46, 1035–1044. [Google Scholar] [CrossRef]
- Kami, A.; Dariani, A.; Sadough Vanini, S.; Comsa, D.; Banabic, D. Application of a GTN Damage Model to Predict the Fracture of Metallic Sheets Subjected to Deep-Drawing. Proc. Rom. Acad.-Ser. A Math. Phys. Tech. Sci. Inf. Sci. 2014, 15, 300–309. [Google Scholar]
- Barrera, C.; Garcia-Herrara, C.; Celentano, D.; Signorelli, J. Material and Damage Characterization of the Elastoplastic Response of the EK4 Deep Drawing Steel. Metals 2022, 12, 720. [Google Scholar] [CrossRef]
- Saxena, R.; Dixit, P. Numerical analysis of damage for prediction of fracture initiation in deep drawing. Finite Elem. Anal. Des. 2011, 47, 1104–1117. [Google Scholar] [CrossRef]
- Nick, M.; Müller, M.; Voigts, H.; Weiser, I.F.; Herrig, T.; Bergs, T. Effect of Friction Modelling on Damage Prediction in Deep Drawing Simulations of Rotationally Symmetric Cups. Defect Diffus. Forum 2022, 414, 103–109. [Google Scholar] [CrossRef]
- Bergs, T.; Nick, M.; Trauth, D.; Klocke, F. Damage Evolution in Nakajima Tests of DP800 Dual Phase Steel. In Proceedings of the International Deep Drawing Research Group 37th Annual Conference, Waterloo, ON, Canada, 3–7 June 2018. [Google Scholar]
- Nick, M.; Feuerhack, A.; Bergs, T.; Clausmeyer, T. Numerical Investigation of Damage in Single-step, Two-step, and Reverse Deep Drawing of Rotationally Symmetric Cups from DP800 Dual Phase Steel. Procedia Manuf. 2020, 47, 636–642. [Google Scholar] [CrossRef]
- Numpon, M.; Sasawat, M. Tearing defect maps for the deep drawing of AISI 304 rectangular cups. Mater. Test. 2020, 62, 769–774. [Google Scholar]
- Soyarslan, C.; Tekkaya, A.E. Finite deformation plasticity coupled with isotropic damage: Formulation in principal axes and applications. Finite Elem. Anal. Des. 2010, 46, 668–683. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Müller, M.; Weiser, I.F.; Herrig, T.; Bergs, T. Numerical Prediction of the Influence of Process Parameters and Process Set-Up on Damage Evolution during Deep Drawing of Rectangular Cups. Eng. Proc. 2022, 26, 6. https://doi.org/10.3390/engproc2022026006
Müller M, Weiser IF, Herrig T, Bergs T. Numerical Prediction of the Influence of Process Parameters and Process Set-Up on Damage Evolution during Deep Drawing of Rectangular Cups. Engineering Proceedings. 2022; 26(1):6. https://doi.org/10.3390/engproc2022026006
Chicago/Turabian StyleMüller, Martina, Ingo Felix Weiser, Tim Herrig, and Thomas Bergs. 2022. "Numerical Prediction of the Influence of Process Parameters and Process Set-Up on Damage Evolution during Deep Drawing of Rectangular Cups" Engineering Proceedings 26, no. 1: 6. https://doi.org/10.3390/engproc2022026006
APA StyleMüller, M., Weiser, I. F., Herrig, T., & Bergs, T. (2022). Numerical Prediction of the Influence of Process Parameters and Process Set-Up on Damage Evolution during Deep Drawing of Rectangular Cups. Engineering Proceedings, 26(1), 6. https://doi.org/10.3390/engproc2022026006




