Motion Planning of a Triple-Link Robotic System ^†

Abstract

The Robogymnast is a complex system formed from a triple-inverted pendulum and mimics the action of a gymnast as they hang by their hands from a high bar and perform progressive upswings to eventually rotate completely around the bar. The three links of the Robogymnast can be compared to the lower limbs, the torso, and the upper limbs of a gymnast, with a single passive joint and two further stepper-motor powered joints. There is sensor equipment attached to the different links to gather data and control signals. While this system has been physically constructed, the current paper describes the approach to automating the 3-link pendulum and describes the system, its parts and setup. Following this, STM32 is applied for programming, system operation and presentation of results.

1. Introduction

The Robogymnast was chosen to represent a complex, underactuated multiple-link mechanical system in order to evaluate and compare control systems based on a range of methods [1]. Designing a control system with underactuation presents challenges because full-state feedback linearisation around a fixed point of equilibrium is often not possible for this type of mechanism, which is also frequently not small-time local controllable (STLC) [2].

This has led to considerable research interest in developing an underactuated system in the fields of control engineering and robotics [3]. Inverted pendulums involve a component which swings freely from a fixed location, and it is suspended under the action of gravitational forces. Work involving regulating movement frequently uses this type of mechanism, and both hybrid and chaotic systems can be demonstrated using this approach [4,5]. An important robotics challenge is presented by the problem of balancing triple-inverted pendulum systems, and this is based on their similarity to the structural and balance factors of the human body. The Acrobat is a robotic system that mimics acrobatic activity in humans, has an inverted pendulum form, and is designed to have instability and underactuation. This makes the robot ideal for theory- and practice-based work on non-linear controls [3,6]. The Acrobat was designed to balance using a specially developed, intelligent controller, which blended conventional control, fuzzy control and adaptive fuzzy control in order to achieve swing, catch and balance in inversion [7]. The controllers tested were based on state variable feedback, as well as proportional-integral-derivative and linear-quadratic regulation approaches.

2. Related Work

The studies presented in [8,9,10,11,12] focus on autonomous upswing for triple-link robots with a single non-actuated joint and two actuated joints. The contribution of this study is to assess movement performance across three links. Such multiple-link inverted pendulum-based systems have various real-world contributions:

-

Such systems can contribute to research investigating problems of movement for disabled or injured individuals, who do not have full use of their arms or legs [13].

-

If such systems could be effectively controlled through the exploitation of the dynamic properties within them, machines could be developed that are more energy efficient and move more smoothly in line with natural moving systems [14] Other studies previously conducted have examined how stability can be achieved in multiple-link robotic systems using a swing mechanism through examining various types of controllers, including Linear–quadratic regulator (LQR) [15], proportional–integral–derivative controller (PID) [16], fuzzy proportional–derivative controller FPD [17], and Fuzzy proportional–integral–derivative controller (FLQR) [18].

The current work makes an original contribution to these issues by implementing and making comparisons between the varied movements found in a 3-link robot across each of the three links. In addition, it presents a new approach to controlling the movement of the pendulum system through synchronising, and it investigates the performance of the stepper motor.

This paper is structured in the following way: the second section provides an overview of related work that have been previously conducted, while the third section first describes the system in general and then discusses its setup further. In Section 4, the results for the motion across each link are examined under various conditions, and the final section provides a summary of the research and presents the conclusions.

3. System Description and Setup

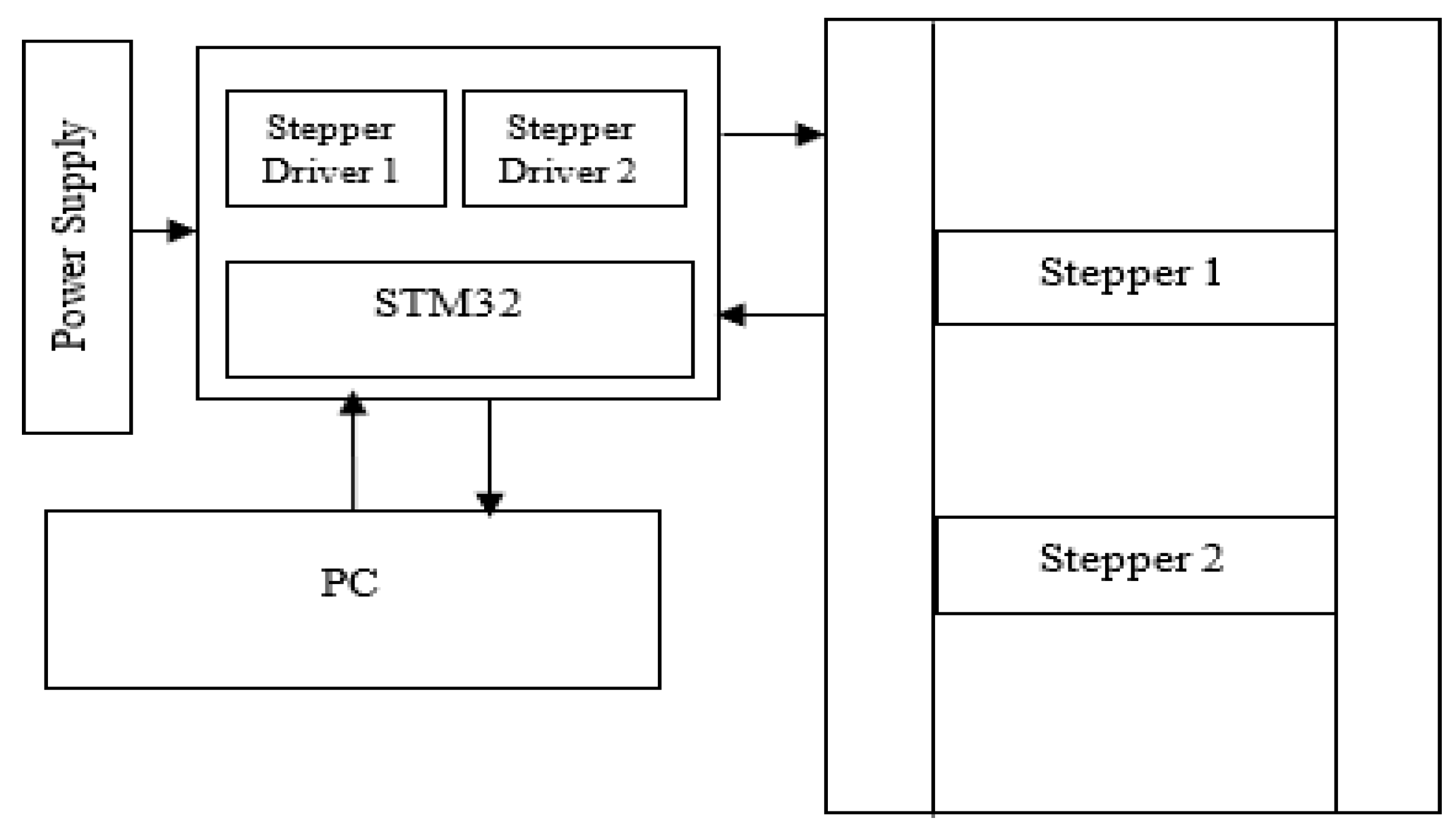
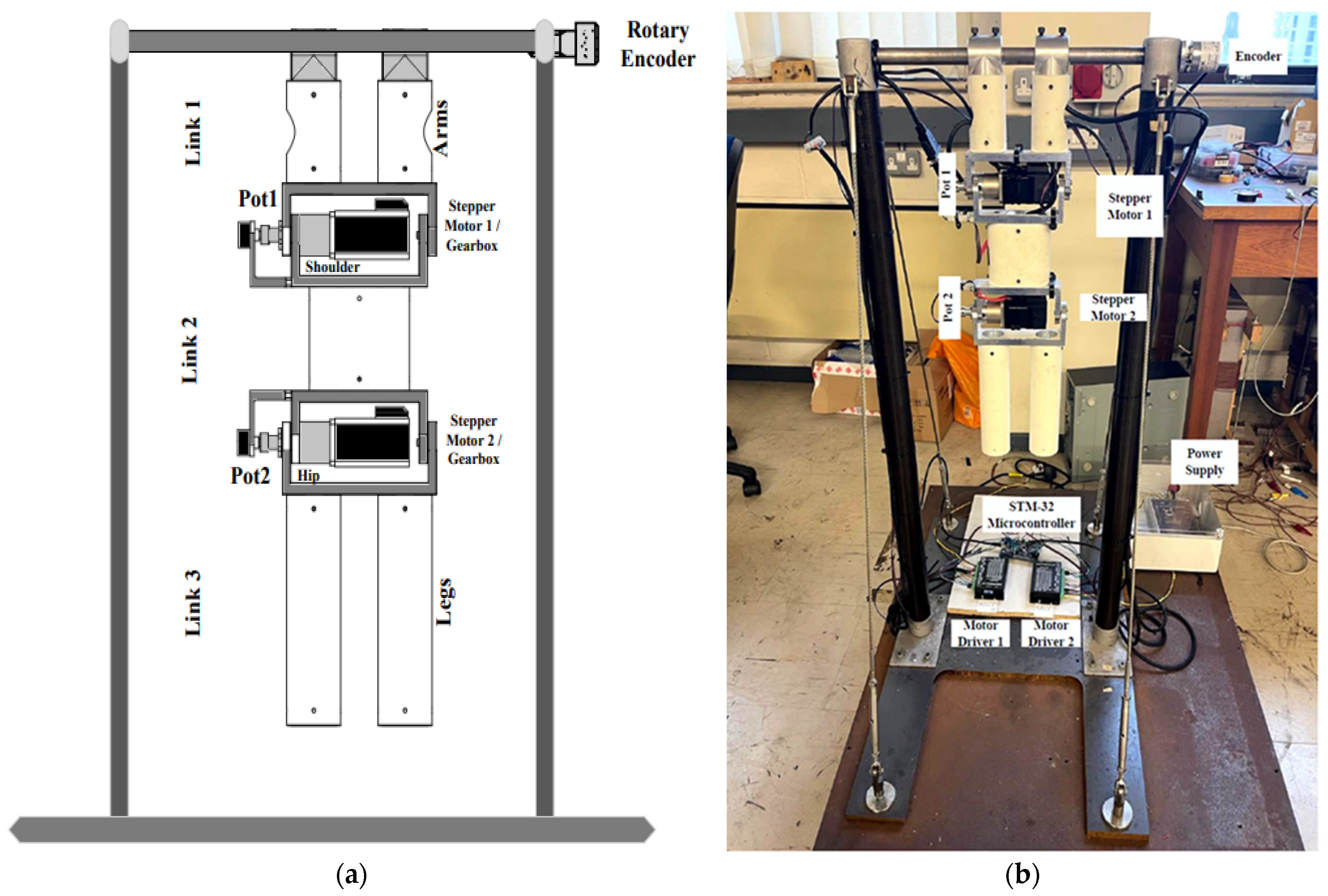
3.1. System Description

This work is applied to a triple-link Robogymnast mechanism, which imitates the gymnastic action of swinging up to freely rotate over a high bar. The diagram given in Figure 1 illustrates the system’s major components, in which the first link is representative of the upper limbs of a gymnast (without modelling the joints at the elbow and wrist); link 2 relates to the head and trunk, as one component without different joints; and link 3 corresponds to the legs, with no joints for the knees and ankles. The Robogymnast’s first joint is unactuated, using passive action, while the remaining two joints, which can be related to a gymnast’s shoulder and hip joints, are active in their operation [13]. Figure 2 illustrates the robotic system through a block diagram, in which it is operates via two stepper motors, with each being subjected to the stepper driver control to achieve smooth movement. The control system programming is performed through the microcontroller STM32 using C++ language for translating commands between the robotic system, the control system and the PC. Each link has its own sensor, and link 1 connects to a rotary encoder, with the remaining links connecting to the potentiometers 2 and 3, respectively, to allow for the detection of absolute angles across every position [15].

Table 1. Robogymnast parameters.

Symbol	Parameters	Mean Value
L1	Length of 1st link	0.16 m
L2	Length of the middle link (link 2)	0.18 m
L3	Length of lower link (link 3)	0.24 m
m1	Weight of link 1	1.2 kg
m2	Weight of link 2	1.2 kg
m3	Weight of lower link 3	0.5 kg
q1, q2, q3	Angles’ initial values	0 (rad)
g	Gravity	9.81 m/s2

. illustrates the Robogymanst parameters in order to length, weight, and angles.

3.2. System Setup

This section considers the setup of the system, where the system itself is attached by connecting to joints 2 and 3 with dual potentiometers as the sensors, and then the header connects with the encoder to detect the absolute value of motion. On the other hand, the operating system, as shown in Figure 1, contains 2 stepper drivers powered by 5v along with programming by an STM-32 microcontroller connecting to a PC to instruct the movement of the system and to read the signal returned from the sensors. Lastly, Figure 2a,b display the Robogymnast’s design diagram and an actual system prepared to run.

4. Results

Discussion

Figure 3a–c demonstrate that each link is in motion simultaneously, in which theta 1 represents the t2 (stepper 1) and t3 (stepper 2) response, based on the opposing motion of the two motors. The second joint is operated by stepper 1, and if it moves in the positive direction, stepper 3 then moves in the opposite direction. In addition to this, the bottom link, which is link 3, is operated by stepper 2, and this begins to reverse at the point when the first motor moves forward, beginning the movements towards upswing of the robot in this system. Based on this,

Table 2. Robogymnast motion results.

Symbol	Parameters	Average (Degrees)°	Max Point (Degrees)°
θ1	Link 1 (free rotate) upper	(−5) to 25	(−45) to 80
θ2	Link 2 (Motor 1) middle	(−5) to 15	(−45) to 25
θ3	Link 3 (Motor 3) lower	(−10) to 10	(−35) to 35

provides the estimated values for the degree of motion in the multiple-link mechanism in both scenarios when, on average, the maximum points in both directions are positive and negative (forward and backward).

5. Conclusions

In this work, planned movement for upswing in a 3-link inverted pendulum-based robot is presented. A description is given of how this system was set up, considering the connection of each component of the system. Subsequent studies will examine this movement further and consider how this 3-link system can be modulated for upswing, as well as developing the controller further for optimisation of the algorithms and their implementation in future work.