Multi-Output Variational Gaussian Process for Daily Forecasting of Hydrological Resources †
Abstract
1. Introduction
2. Mathematical Framework
2.1. Gaussian Process Modeling Framework
2.2. Multi-Output Gaussian Process (MOGP)
2.3. Variational Gaussian Process (VGP)
3. Results and Discussions
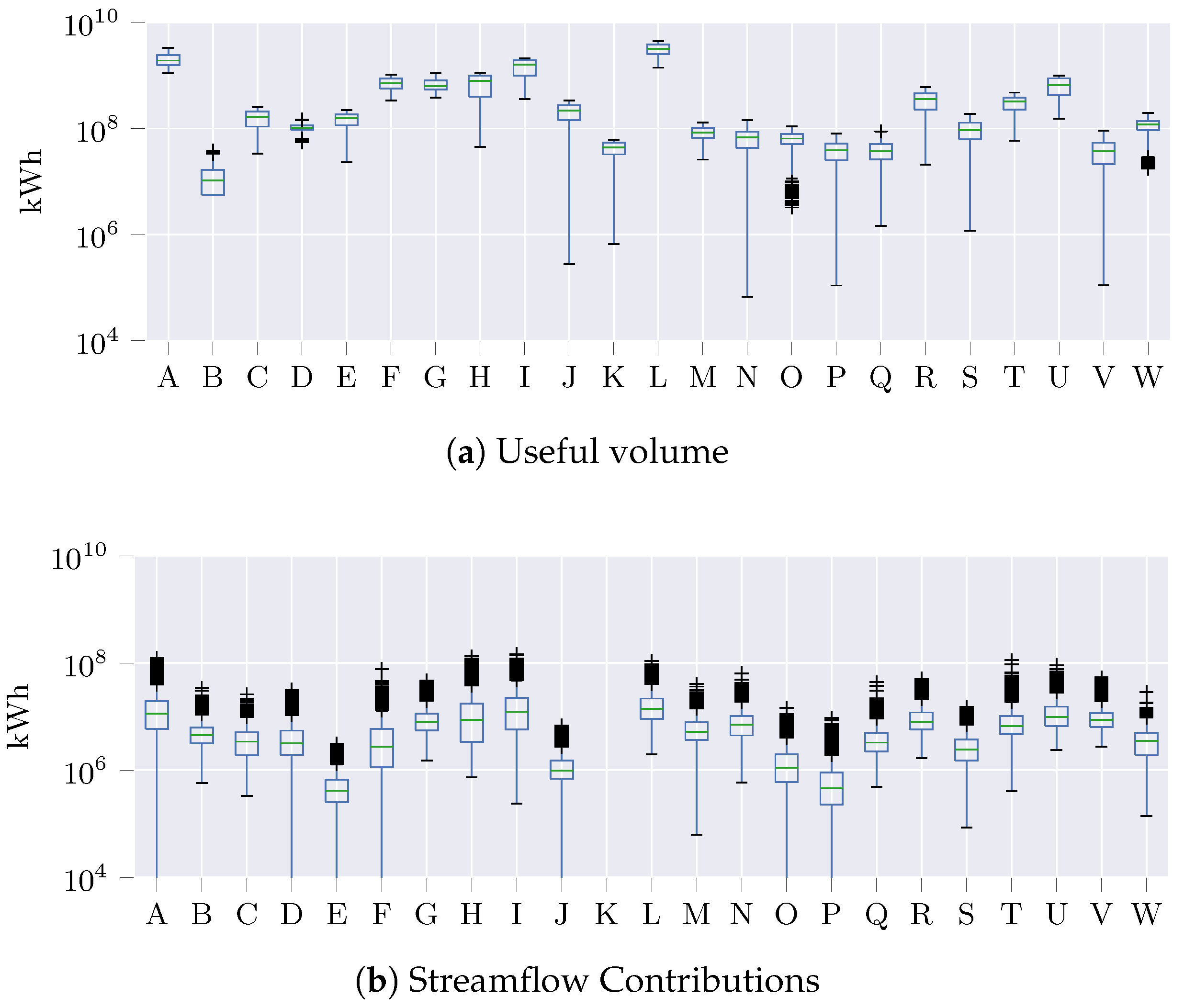
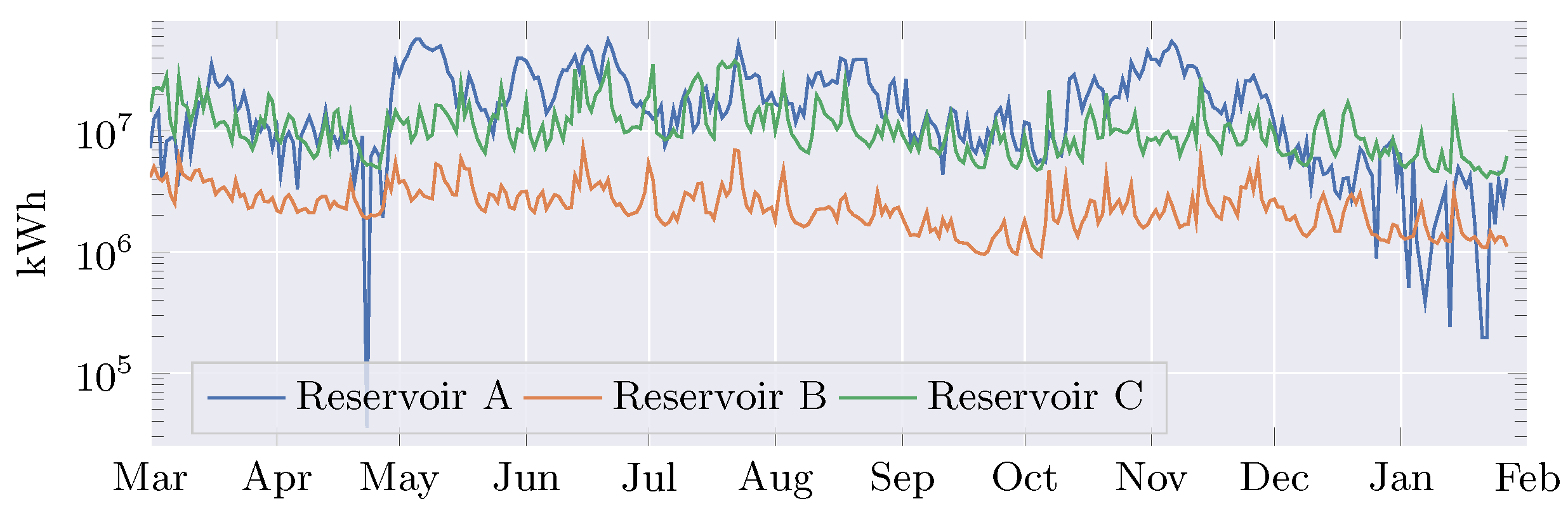
3.1. Dataset Collection
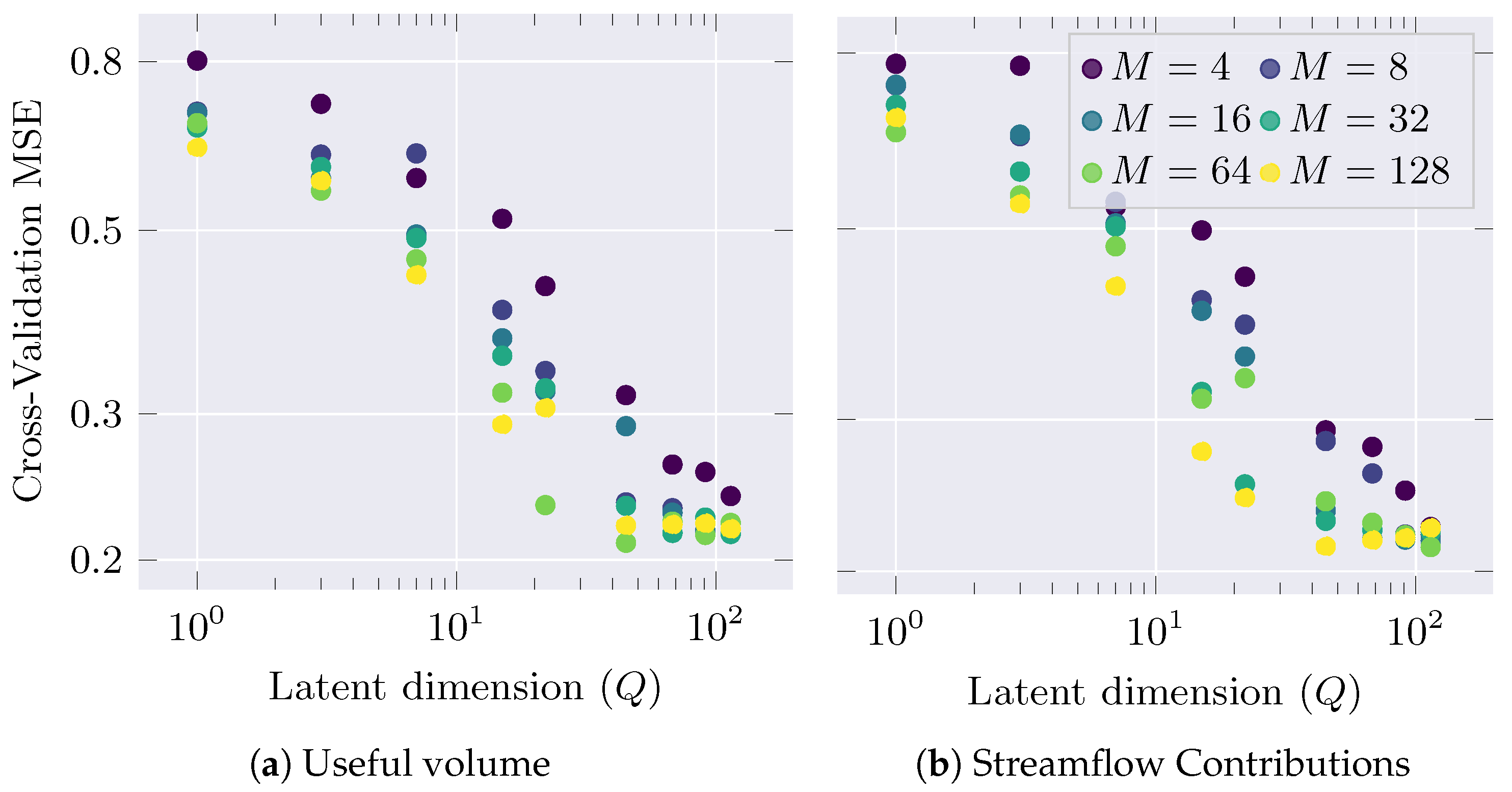
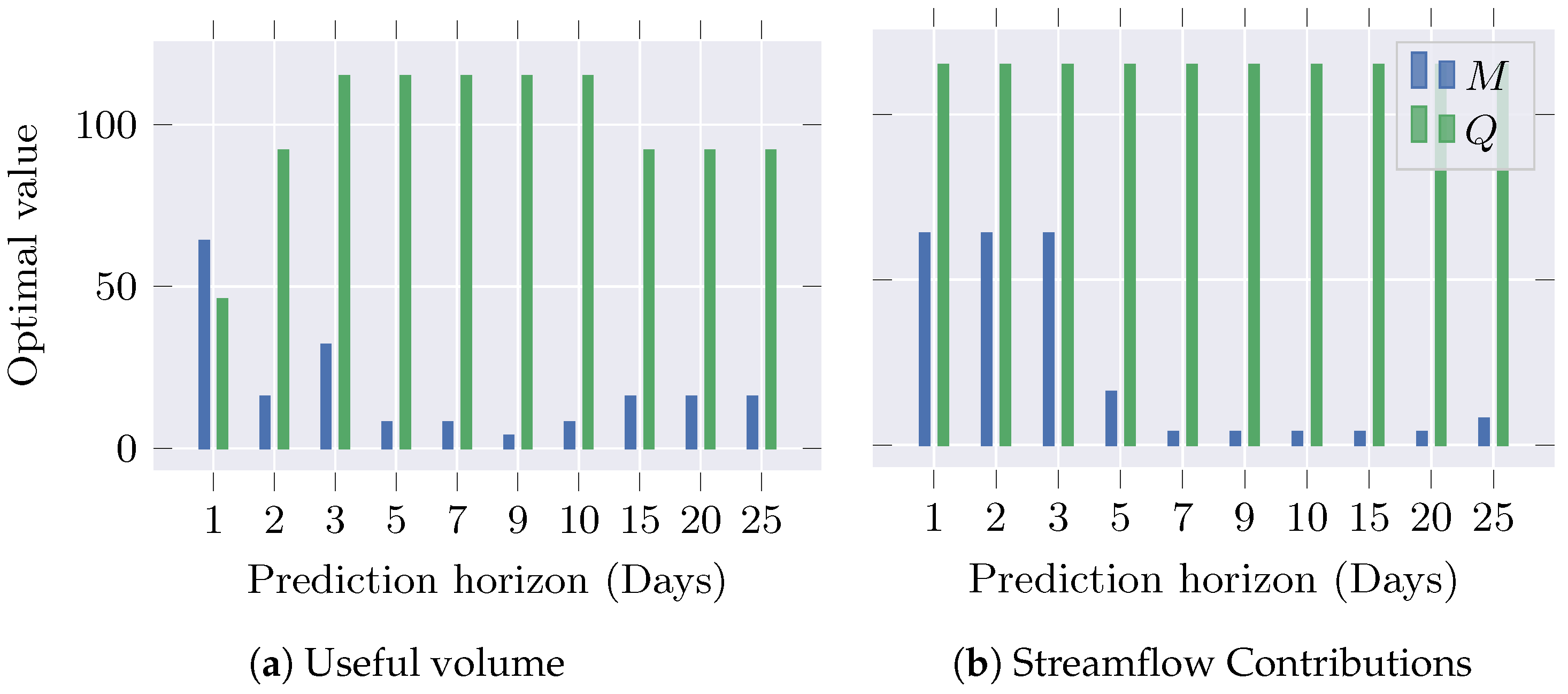
3.2. MOVGP Setup and Hyperparameter Tuning
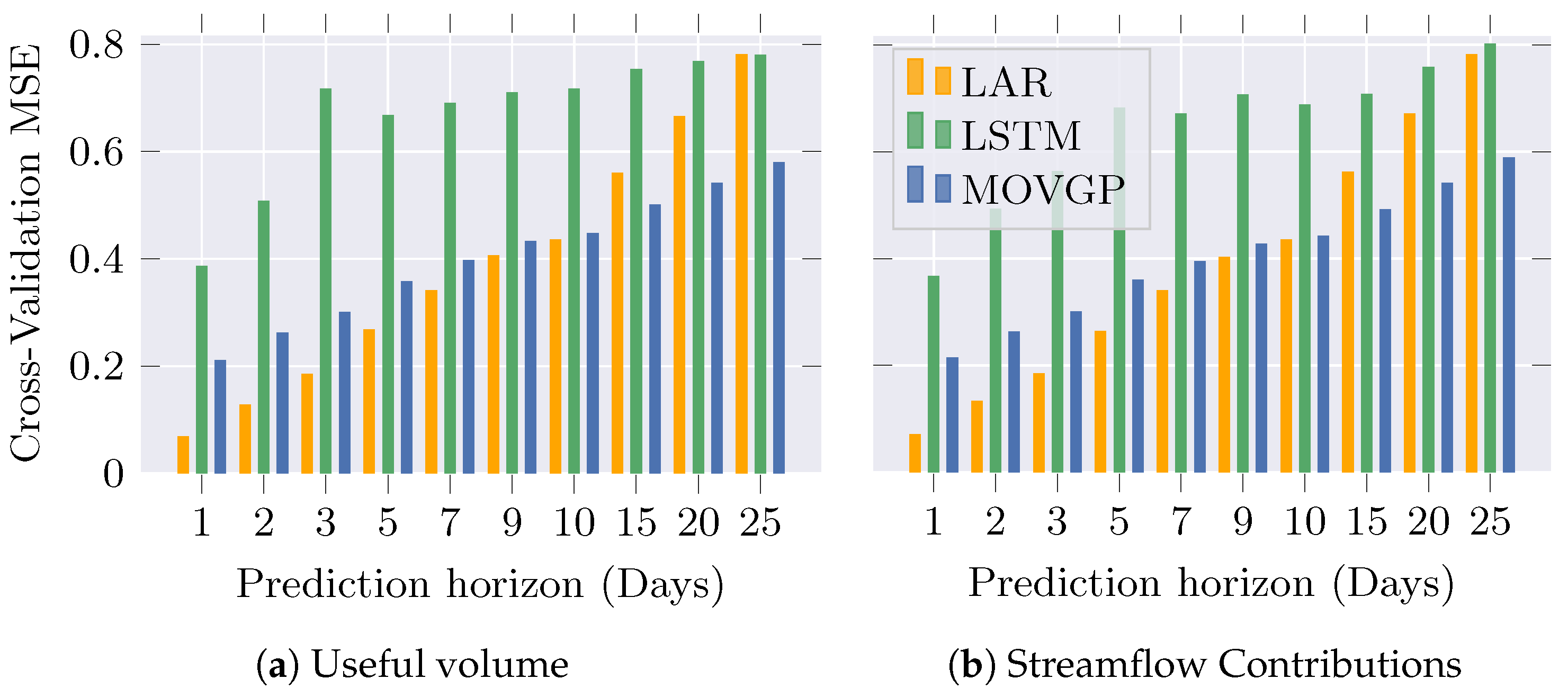
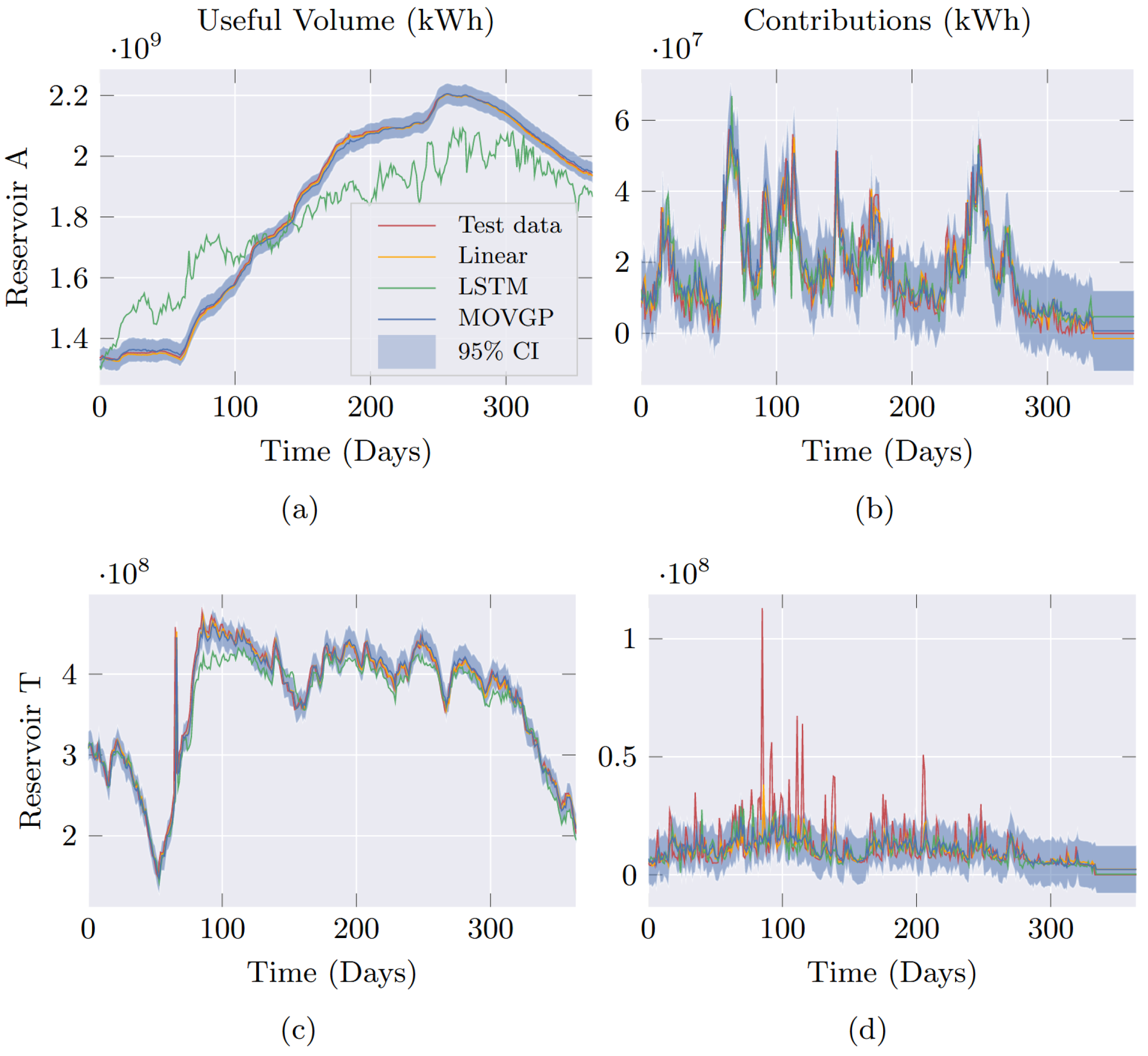
3.3. Performance Analysis
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Basu, M. Improved differential evolution for short-term hydrothermal scheduling. Int. J. Electr. Power Energy Syst. 2014, 58, 91–100. [Google Scholar] [CrossRef]
- Nazari-Heris, M.; Mohammadi-Ivatloo, B.; Gharehpetian, G.B. Short-term scheduling of hydro-based power plants considering application of heuristic algorithms: A comprehensive review. Renew. Sustain. Energy Rev. 2017, 74, 116–129. [Google Scholar] [CrossRef]
- Freire, P.K.D.M.M.; Santos, C.A.G.; Silva, G.B.L.D. Analysis of the use of discrete wavelet transforms coupled with ANN for short-term streamflow forecasting. Appl. Soft Comput. J. 2019, 80, 494–505. [Google Scholar] [CrossRef]
- XM. La Generación de Energía en enero fue de 6276.74 gwh. 2022. Available online: https://www.xm.com.co/noticias/4630-la-generacion-de-energia-en-enero-fue-de-627674-gwh (accessed on 7 November 2022).
- Cheng, M.; Fang, F.; Kinouchi, T.; Navon, I.; Pain, C. Long lead-time daily and monthly streamflow forecasting using machine learning methods. J. Hydrol. 2020, 590, 125376. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Allawi, M.F.; Yousif, A.A.; Jaafar, O.; Hamzah, F.M.; El-Shafie, A. Non-tuned machine learning approach for hydrological time series forecasting. Neural Comput. Appl. 2018, 30, 1479–1491. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K.W. Flood prediction using machine learning models: Literature review. Water 2018, 10, 1536. [Google Scholar] [CrossRef]
- Apaydin, H.; Feizi, H.; Sattari, M.T.; Colak, M.S.; Shamshirband, S.; Chau, K. Comparative analysis of recurrent neural network architectures for reservoir inflow forecasting. Water 2020, 12, 1500. [Google Scholar] [CrossRef]
- Zhu, S.; Luo, X.; Xu, Z.; Ye, L. Seasonal streamflow forecasts using mixture-kernel GPR and advanced methods of input variable selection. Hydrol. Res. 2019, 50, 200–214. [Google Scholar] [CrossRef]
- Saraiva, S.V.; de Oliveira Carvalho, F.; Santos, C.A.G.; Barreto, L.C.; de Macedo Machado Freire, P.K. Daily streamflow forecasting in Sobradinho Reservoir using machine learning models coupled with wavelet transform and bootstrapping. Appl. Soft Comput. 2021, 102, 107081. [Google Scholar] [CrossRef]
- Ni, L.; Wang, D.; Wu, J.; Wang, Y.; Tao, Y.; Zhang, J.; Liu, J. Streamflow forecasting using extreme gradient boosting model coupled with Gaussian mixture model. J. Hydrol. 2020, 586, 124901. [Google Scholar] [CrossRef]
- Sun, A.Y.; Wang, D.; Xu, X. Monthly streamflow forecasting using Gaussian process regression. J. Hydrol. 2014, 511, 72–81. [Google Scholar] [CrossRef]
- Niu, W.; Feng, Z. Evaluating the performances of several artificial intelligence methods in forecasting daily streamflow time series for sustainable water resources management. Sustain. Cities Soc. 2021, 64, 102562. [Google Scholar] [CrossRef]
- Zhu, S.; Luo, X.; Yuan, X.; Xu, Z. An improved long short-term memory network for streamflow forecasting in the upper Yangtze River. Stoch. Environ. Res. Risk Assess. 2020, 34, 1313–1329. [Google Scholar] [CrossRef]
- Moreno-Muñoz, P.; Artés, A.; Álvarez, M. Heterogeneous Multi-output Gaussian Process Prediction. In Proceedings of the Advances in Neural Information Processing Systems; Bengio, S., Wallach, H., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R., Eds.; Curran Associates, Inc.: New York, NY, USA, 2018; Volume 31. [Google Scholar]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; Adaptive Computation and Machine Learning; MIT Press: Cambridge, MA, USA, 2006; pp. 1–248. [Google Scholar]
- Liu, H.; Cai, J.; Ong, Y.S. Remarks on multi-output Gaussian process regression. Knowl.-Based Syst. 2018, 144, 102–121. [Google Scholar] [CrossRef]
- Álvarez, M.A.; Rosasco, L.; Lawrence, N.D. Kernels for Vector-Valued Functions: A Review. Found. Trends® Mach. Learn. 2012, 4, 195–266. [Google Scholar] [CrossRef]
- Hensman, J.; Fusi, N.; Lawrence, N.D. Gaussian Processes for Big Data. arXiv 2013, arXiv:1309.6835. [Google Scholar] [CrossRef]
- Hensman, J.; Matthews, A.; Ghahramani, Z. Scalable Variational Gaussian Process Classification. arXiv 2014, arXiv:1411.2005. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pastrana-Cortés, J.D.; Cardenas-Peña, D.A.; Holguín-Londoño, M.; Castellanos-Dominguez, G.; Orozco-Gutiérrez, Á.A. Multi-Output Variational Gaussian Process for Daily Forecasting of Hydrological Resources. Eng. Proc. 2023, 39, 83. https://doi.org/10.3390/engproc2023039083
Pastrana-Cortés JD, Cardenas-Peña DA, Holguín-Londoño M, Castellanos-Dominguez G, Orozco-Gutiérrez ÁA. Multi-Output Variational Gaussian Process for Daily Forecasting of Hydrological Resources. Engineering Proceedings. 2023; 39(1):83. https://doi.org/10.3390/engproc2023039083
Chicago/Turabian StylePastrana-Cortés, Julián David, David Augusto Cardenas-Peña, Mauricio Holguín-Londoño, Germán Castellanos-Dominguez, and Álvaro Angel Orozco-Gutiérrez. 2023. "Multi-Output Variational Gaussian Process for Daily Forecasting of Hydrological Resources" Engineering Proceedings 39, no. 1: 83. https://doi.org/10.3390/engproc2023039083
APA StylePastrana-Cortés, J. D., Cardenas-Peña, D. A., Holguín-Londoño, M., Castellanos-Dominguez, G., & Orozco-Gutiérrez, Á. A. (2023). Multi-Output Variational Gaussian Process for Daily Forecasting of Hydrological Resources. Engineering Proceedings, 39(1), 83. https://doi.org/10.3390/engproc2023039083





