Utility of Field Weakening and Field-Oriented Control in Permanent-Magnet Synchronous Motors: A Case Study †
Abstract
1. Introduction
2. Materials and Methods
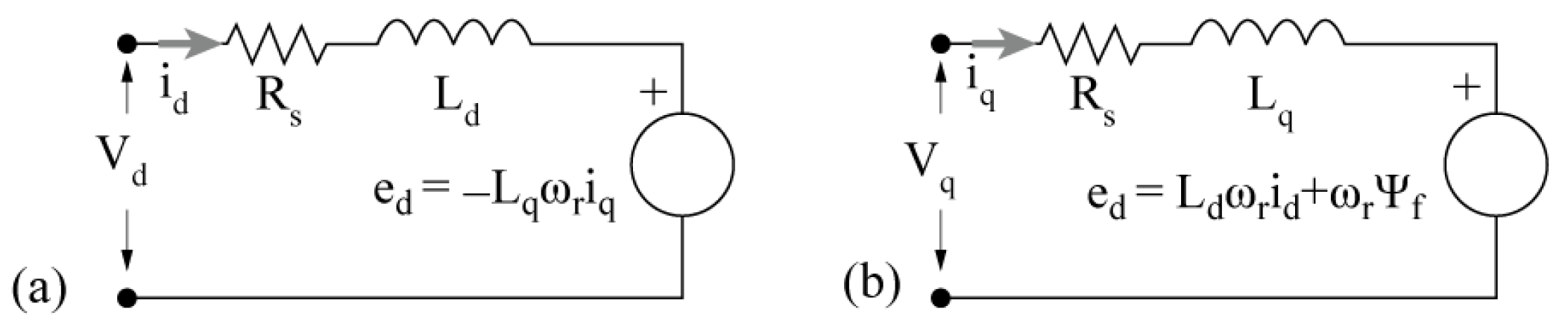
2.1. PMSM-BLAC Motor Modelling
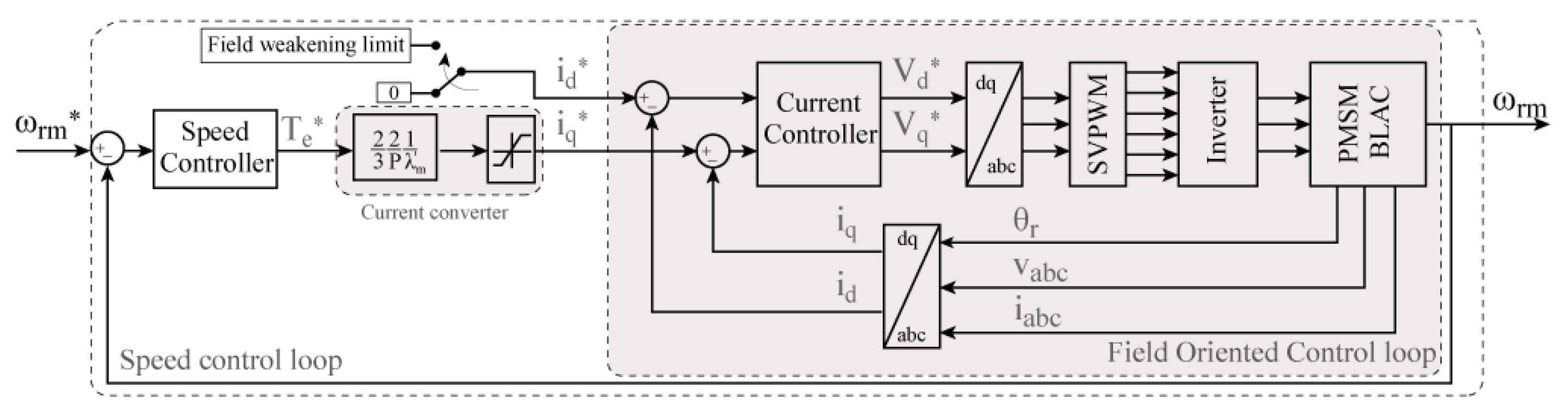
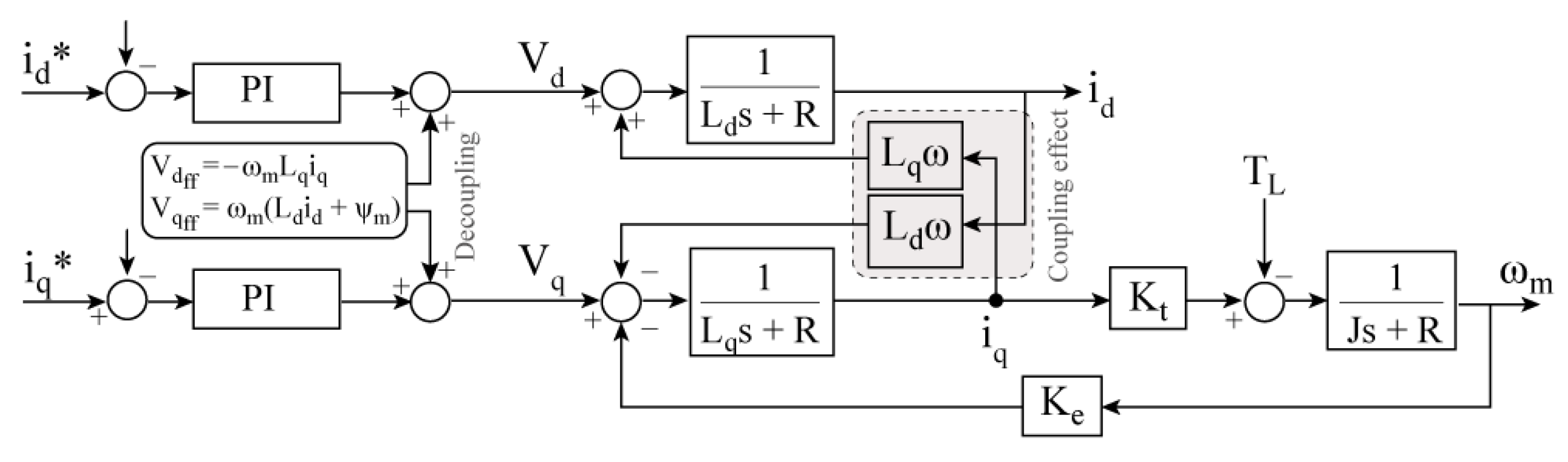
2.2. Vectorial Field-Oriented Control
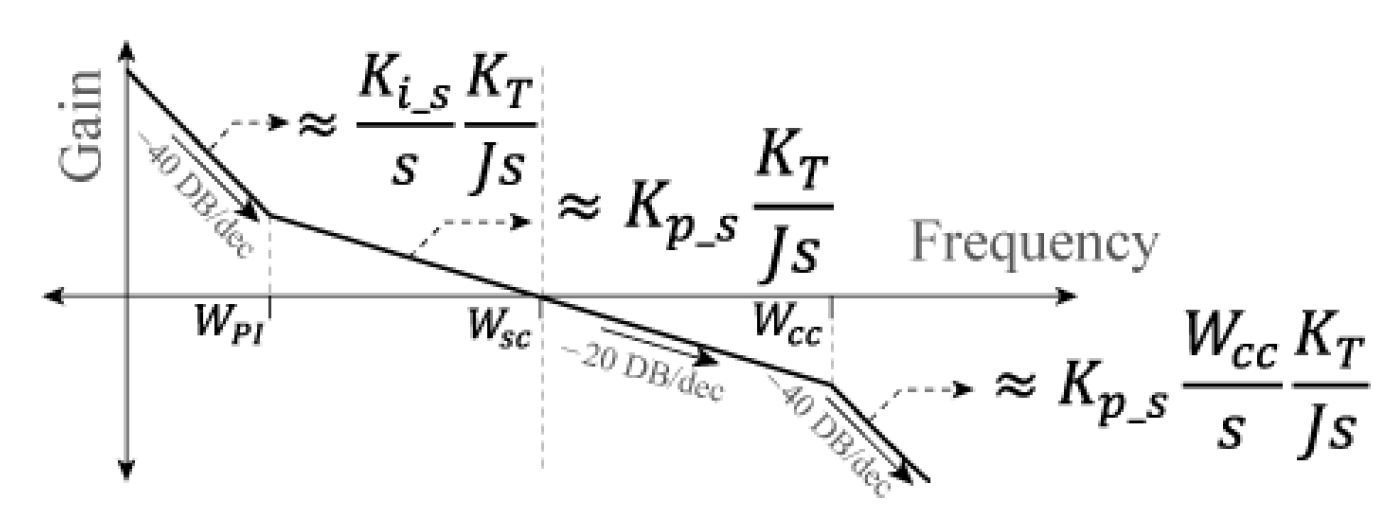
2.3. Speed Control
2.4. Vector Space Pulse Width Modulation
3. Results and Discussion
3.1. Internal Current Control Loop Tests
3.2. Velocity Control Loop Tests
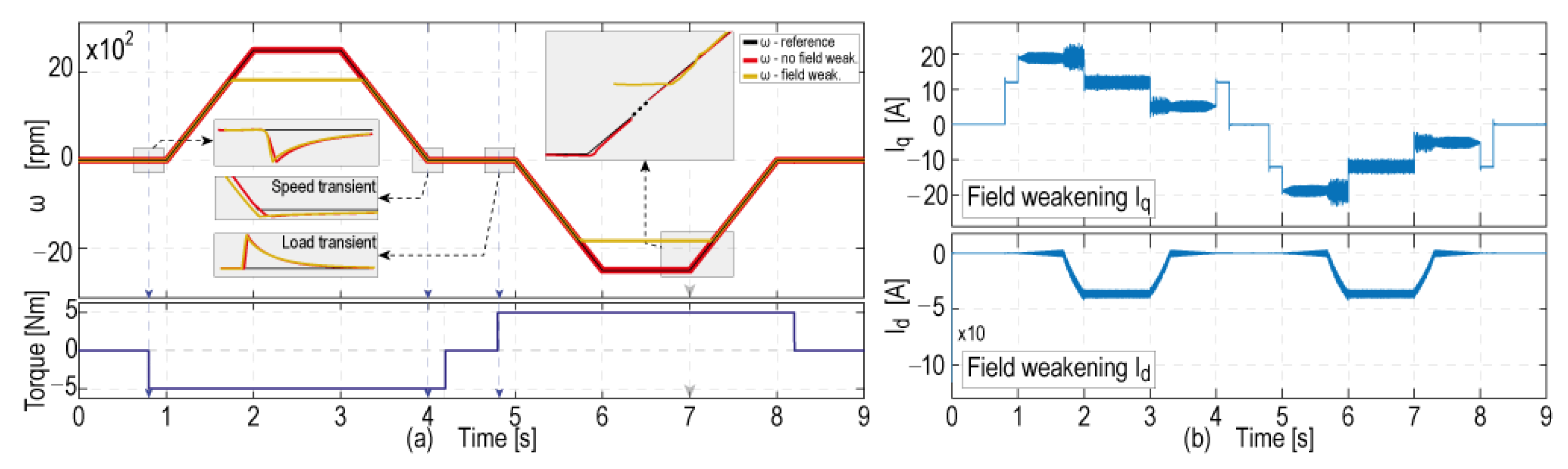
3.3. System Tests including Field Weakening
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gómez Misnaza, C.D. Diseño y Simulación del Control por Orientación de Campo FOC para un Motor Síncrono de Imanes Permanentes tipo BLAC. Bachelor’s Thesis, EPN, Quito, Ecuador, 2020. Available online: http://bibdigital.epn.edu.ec/handle/15000/21220 (accessed on 1 August 2023).
- Sepulchre, L.; Fadel, M.; Pietrzak-David, M.; Porte, G. Flux-weakening strategy for high speed PMSM for vehicle application. In Proceedings of the 2016 International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), Toulouse, France, 2–4 November 2016; pp. 1–7. [Google Scholar] [CrossRef]
- Eriksson, S. Drive systems with permanent magnet synchronous motors. Automot. Eng. 1995, 103. Available online: https://www.osti.gov/biblio/37082 (accessed on 1 August 2023).
- Loganayaki, A.; Kumar, R.B. Permanent Magnet Synchronous Motor for Electric Vehicle Applications. In Proceedings of the 2019 5th International Conference on Advanced Computing & Communication Systems (ICACCS), Coimbatore, India, 15–16 March 2019; pp. 1064–1069. [Google Scholar] [CrossRef]
- DC, Induction, Reluctance and PM Motors for Electric Vehicles|IET Journals & Magazine|IEEE Xplore. Available online: https://ieeexplore.ieee.org/document/281755 (accessed on 1 August 2023).
- Chalmers, B.J.; Musaba, L.; Gosden, D.F. Variable-frequency synchronous motor drives for electric vehicles. IEEE Trans. Ind. Appl. 1996, 32, 896–903. [Google Scholar] [CrossRef]
- Liu, X.; Chen, H.; Zhao, J.; Belahcen, A. Research on the Performances and Parameters of Interior PMSM Used for Electric Vehicles. IEEE Trans. Ind. Electron. 2016, 63, 3533–3545. [Google Scholar] [CrossRef]
- Abu-Rub, H.; Iqbal, A.; Guzinski, J. High Performance Control of AC Drives with Matlab/Simulink Models; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Kim, S.-H. Electric Motor Control: DC, AC, and BLDC Motors; Elsevier: Amsterdam, The Netherlands, 2017; p. 426. [Google Scholar]
- Krause, P.C.; Wasynczuk, O.; Sudhoff, S.D.; Pekarek, S.D. Analysis of Electric Machinery and Drive Systems; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Odo, K.; Vincent, E.S.; Ogbuka, C. A Model-based PI Controller Tuning and Design for Field Oriented Current Control of Permanent Magnet Synchronous Motor. IOSR J. Electr. Electr. Eng. (IOSR-JEEE) 2019, 14, 35–41. [Google Scholar] [CrossRef]
- Kim, S.A.; Song, J.H.; Han, S.W.; Cho, Y.H. An Improved Dynamic Modeling of Permanent Magnet Synchronous Machine with Torque Ripple Characteristics. J. Clean Energy Technol. 2018, 6, 117–120. [Google Scholar] [CrossRef]
- Zhao, Y. Application of Sliding Mode Controller and Linear Active Disturbance Rejection Controller to a PMSM Speed System. Mater Thesis, Cleveland State University, Cleveland, OH, USA, 2009. [Google Scholar]
- Mukti, E.W.; Wijanarko, S.; Muqorobin, A.; Rozaqi, L. Field oriented control design of inset rotor PMSM drive. AIP Conf. Proc. 2017, 1855, 020010. [Google Scholar] [CrossRef]
- Taha, M.; Osama, A.M.; Zaid, S. Simulation Study of a New Approach for Field Weakening Control of PMSM. J. Power Electron. 2012, 12, 136–144. [Google Scholar] [CrossRef]
- Chau, K.T. Electric Vehicle Machines and Drives: Design, Analysis and Application; John Wiley & Sons: Hoboken, NJ, USA, 2015; p. 400. [Google Scholar] [CrossRef]
- Bida, V.; Samokhvalov, D.; Al-Mahturi, F. PMSM vector control techniques—A survey. In Proceedings of the 2018 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), Moscow and St. Petersburg, Russia, 29 January–1 February 2018; pp. 577–581. [Google Scholar] [CrossRef]
- Amin, F.; Sulaiman, E.; Mulyo Utomo, W.; Soomro, H.; Jenal, M.; Kumar, R. Modelling and Simulation of Field Oriented Control Based Permanent Magnet Synchronous Motor Drive System. Indones. J. Electr. Eng. Comput. Sci. 2017, 6, 387–395. [Google Scholar] [CrossRef]
- Mulyo Utomo, W.; Muhammad Zin, N.; Haron, Z.; Sy Yi, S.; Bohari, A.; Mat Ariff, R.; Hanafi, D. Speed Tracking of Field Oriented Control Permanent Magnet Synchronous Motor Using Neural Network. Int. J. Power Electron. Drive Syst. IJPEDS 2014, 4, 290. [Google Scholar] [CrossRef][Green Version]
- Boudjemaa, M.; Chenni, R. Field Oriented Control of PMSM Supplied by Photovoltaic Source. Int. J. Electr. Comput. Eng. IJECE 2016, 6, 1233. [Google Scholar] [CrossRef]
- Ahmadian, A.; Ghanbari, M.; Rastegar, H. Field-oriented Control of Permanent Magnet Synchronous Motor with Optimum Proportional-Integrator-Derivative Controller Using Dynamic Particle Swarm Optimization Algorithm. Sci. Int. 2014, 27, 155–158. [Google Scholar]
- Morales-Caporal, R.; Ordoñez-Flores, R.; Huerta, E.; Hernandez, J.; Sandre Hernandez, O. Simulación del Control por Campo Orientado y del Control Directo del par de un Servomotor Síncrono de Imanes Permanentes con Control Inteligente de Velocidad. In Proceedings of the IX Congreso Internacional sobre Innovación y Desarrollo Tecnológico, Cuernavaca Morelos, México, 23–25 November 2011. [Google Scholar]
- Liu, T.; Tan, Y.; Wu, G.; Wang, S. Simulation of PMSM Vector Control System Based on Matlab/Simulink. In Proceedings of the 2009 International Conference on Measuring Technology and Mechatronics Automation, Zhangjiajie, China, 11–12 April 2009; pp. 343–346. [Google Scholar] [CrossRef]
- Qu, L.; Qiao, W.; Qu, L. An Enhanced Linear Active Disturbance Rejection Rotor Position Sensorless Control for Permanent Magnet Synchronous Motors. IEEE Trans. Power Electron. 2019, 35, 6175–6184. [Google Scholar] [CrossRef]
- Zigmund, B.; Terlizzi, A.A.; del T, X.; Pavlanin, R.; Salvatore, L. Experimental Evaluation of PI Tuning Techniques for Field Oriented Control of Permanent Magnet Synchronous Motors. Adv. Electr. Electron. Eng. 2011, 5, 114–119. [Google Scholar]
- Lukichev, D.; Demidova, G. Features of tuning strategy for field oriented control of PMSM position drive system with two-mass load. Int. J. Circuits Syst. Signal Proc. 2016, 10, 88–94. [Google Scholar]
- Papadopoulos, K.G. PID Controller Tuning Using the Magnitude Optimum Criterion; Springer: Cham, Switzerland, 2015; ISBN 978-3-319-07262-3. [Google Scholar]
- Yong-Bin, W.; Xiao-Dong, H.; Yi, C.; Xin-Qi, X. A MPC Method Based on the Oval Invariant Set for PMSM Speed Control System. In Proceedings of the 2016 International Symposium on Computer, Consumer and Control (IS3C), Xi’an, China, 4–6 July 2016; pp. 575–578. [Google Scholar]
- Sidda, S.; Kiranmayi, R.; Mandadi, P. Investigation of PI and Fuzzy Controllers for Speed Control of PMSM Motor Drive. In Proceedings of the 2018 International Conference on Recent Trends in Electrical, Control and Communication (RTECC), Malaysia, Malaysia, 20–22 March 2018; pp. 133–136. [Google Scholar]
- Cui, B.; Han, Z.; Li, J.; Mu, J. Research on PMSM Speed Control System Based on Improved Reaching Law. In Proceedings of the 2019 3rd International Conference on Circuits, System and Simulation (ICCSS), Nanjing, China, 13–15 June 2019; pp. 19–24. [Google Scholar] [CrossRef]
- Krishnan, R. Permanent Magnet Synchronous and Brushless DC Motor Drives, 1st ed.; CRC Press: Boca Raton, FL, USA, 2017; ISBN 978-1-315-22148-9. [Google Scholar] [CrossRef]
- Phung Quang, N.; Dittrich, J.-A. Vector Control of Three-Phase AC Machines-System Development in the Practice; Springer: Berlin/Heidelberg, Germany, 2015; ISBN 978-3-662-46914-9. [Google Scholar]
- Muhammad, H.R. Power electronics: Circuits, devices, and applications. Choice Rev. Online 1989, 26, 26. [Google Scholar]
- Uçak, O.; Yilmaz, S. Implementation of Space Vector PWM In FOC of a Servo Motor Drive. Available online: www.eleco.org.tr/openconf_2015/modules/request.php?module=oc_proceedings&action=view.php&id=111&a=Accept+as+Poster (accessed on 5 August 2023).



| Characteristic | Value | Unit | Characteristic | Value | Unit |
|---|---|---|---|---|---|
| Topology | Surface-mounted permanent-magnet synchronous machine | N/A | Voltage | 120 | [V] |
| Pole pairs | 7 | N/A | Synchronous inductance | 0.344 | [mH] |
| Connection type | Star | N/A | Magnetic flux constant | 39.6 | [mWb] |
| Resistance/phase | 22.2 | [mΩ] | Nominal velocity | 1590 | [rpm] |
| Inertia | 0.008 | [Kgm2] | Max. Current | 121 | [A] |
| Locked Rotor Test | Speed Control Test | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Fcc (Hz) | Id | Iq | Fcc (Hz) | Speed | Id | Iq | |||||
| ISE | Settling Time | ISE | ISE | ISE | Settling Time | ISE | Settling Time | ISE | Settling Time | ||
| 500 | 2.68 | 35 ms | 0.018 | 15 ms | 800 | 0.14 | 120 ms | 2.52 | 25 ms | 0.012 | 11 ms |
| 800 | 2.52 | 25 ms | 0.012 | 11 ms | 1000 | 0.125 | 103 ms | 2.5 | 20 ms | 0.009 | 8 ms |
| 1000 | 2.5 | 20 ms | 0.009 | 8 ms | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Medina, J.; Gómez, C.; Pozo, M.; Chamorro, W.; Tibanlombo, V. Utility of Field Weakening and Field-Oriented Control in Permanent-Magnet Synchronous Motors: A Case Study. Eng. Proc. 2023, 47, 17. https://doi.org/10.3390/engproc2023047017
Medina J, Gómez C, Pozo M, Chamorro W, Tibanlombo V. Utility of Field Weakening and Field-Oriented Control in Permanent-Magnet Synchronous Motors: A Case Study. Engineering Proceedings. 2023; 47(1):17. https://doi.org/10.3390/engproc2023047017
Chicago/Turabian StyleMedina, Jorge, Christian Gómez, Marcelo Pozo, William Chamorro, and Victor Tibanlombo. 2023. "Utility of Field Weakening and Field-Oriented Control in Permanent-Magnet Synchronous Motors: A Case Study" Engineering Proceedings 47, no. 1: 17. https://doi.org/10.3390/engproc2023047017
APA StyleMedina, J., Gómez, C., Pozo, M., Chamorro, W., & Tibanlombo, V. (2023). Utility of Field Weakening and Field-Oriented Control in Permanent-Magnet Synchronous Motors: A Case Study. Engineering Proceedings, 47(1), 17. https://doi.org/10.3390/engproc2023047017






