Analyzing Seasonality in Hydropower Plants Energy Production and External Variables †
Abstract
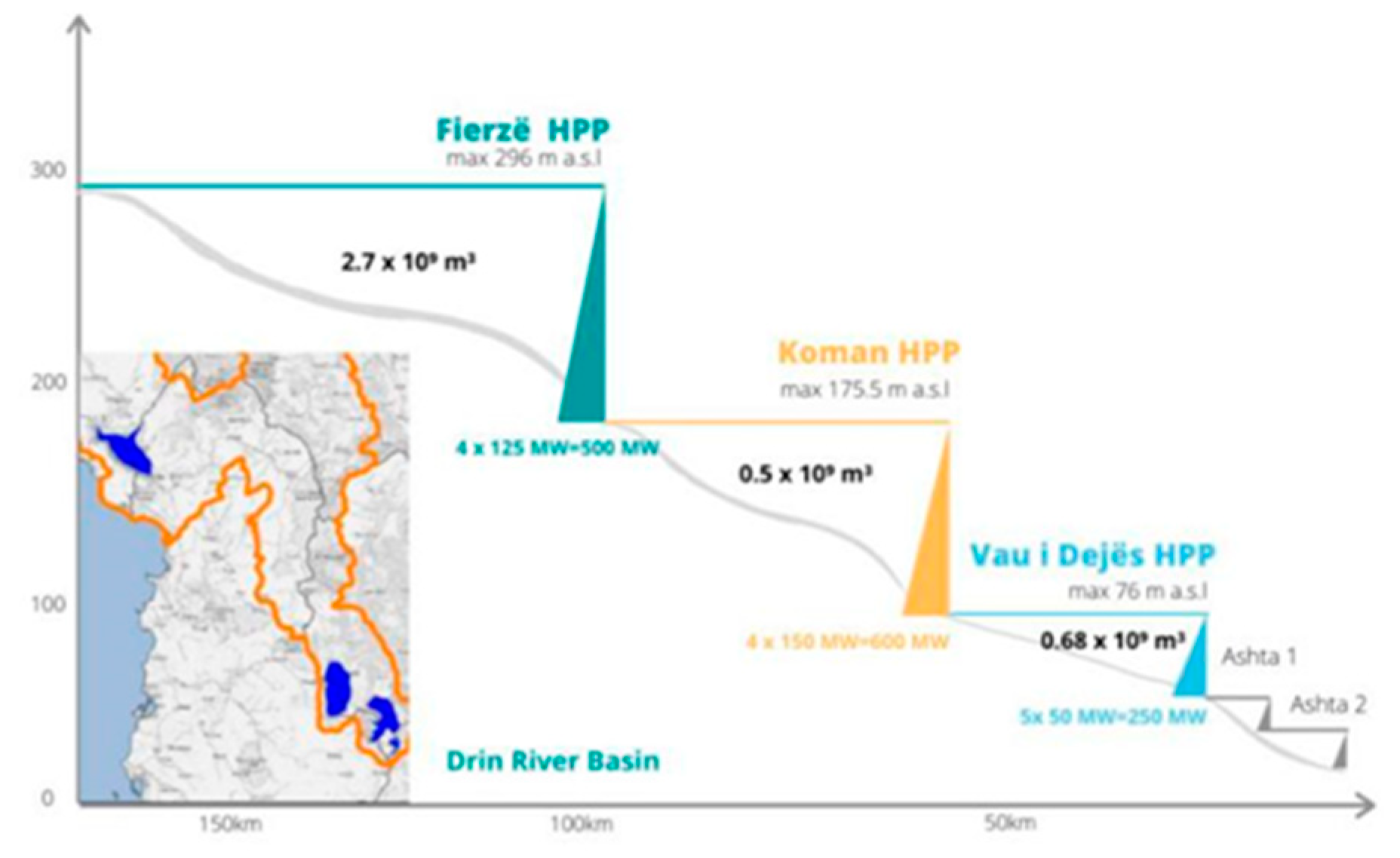
1. Introduction
2. Objective of the Study
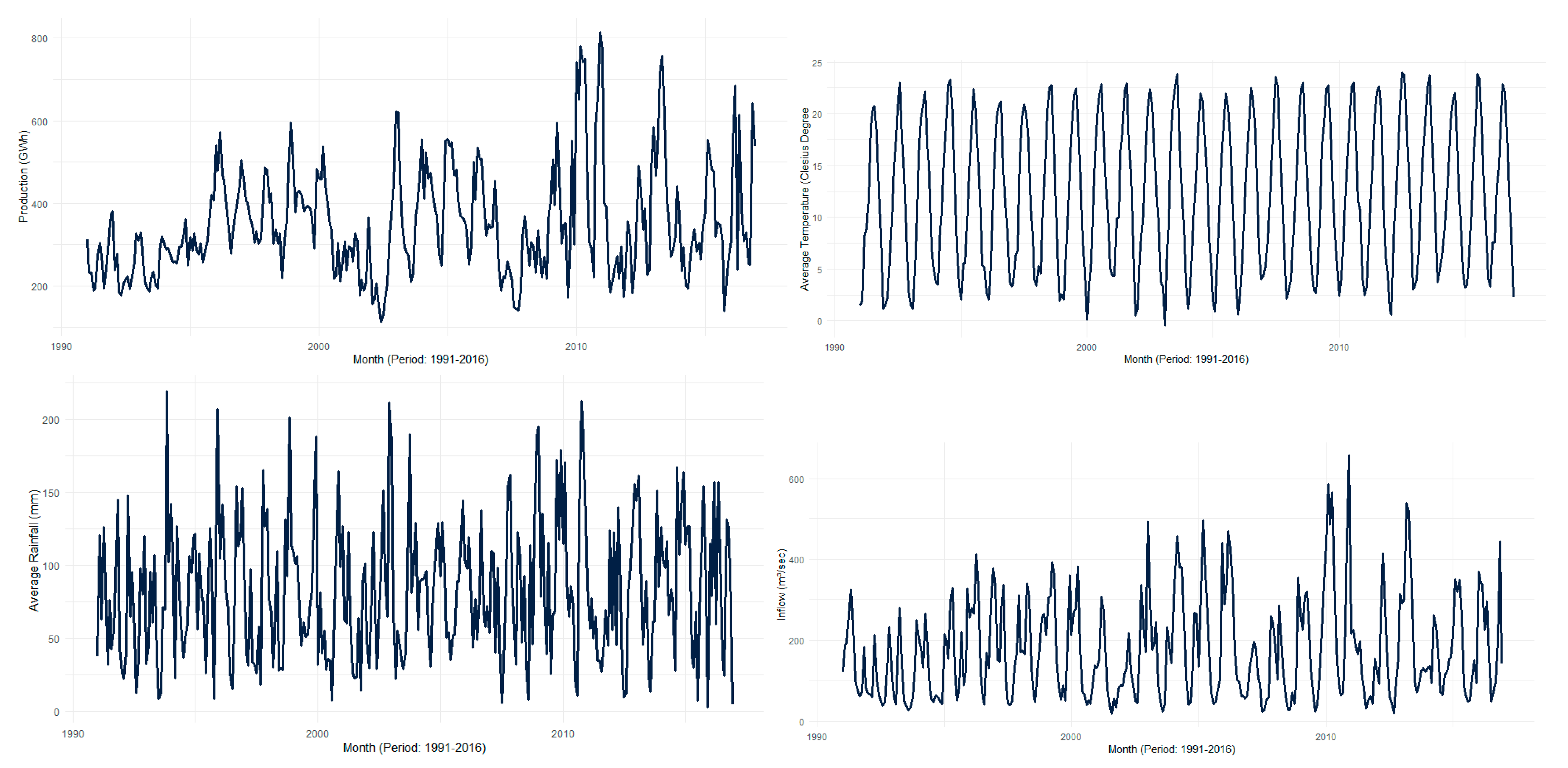
3. Time Series Analysis
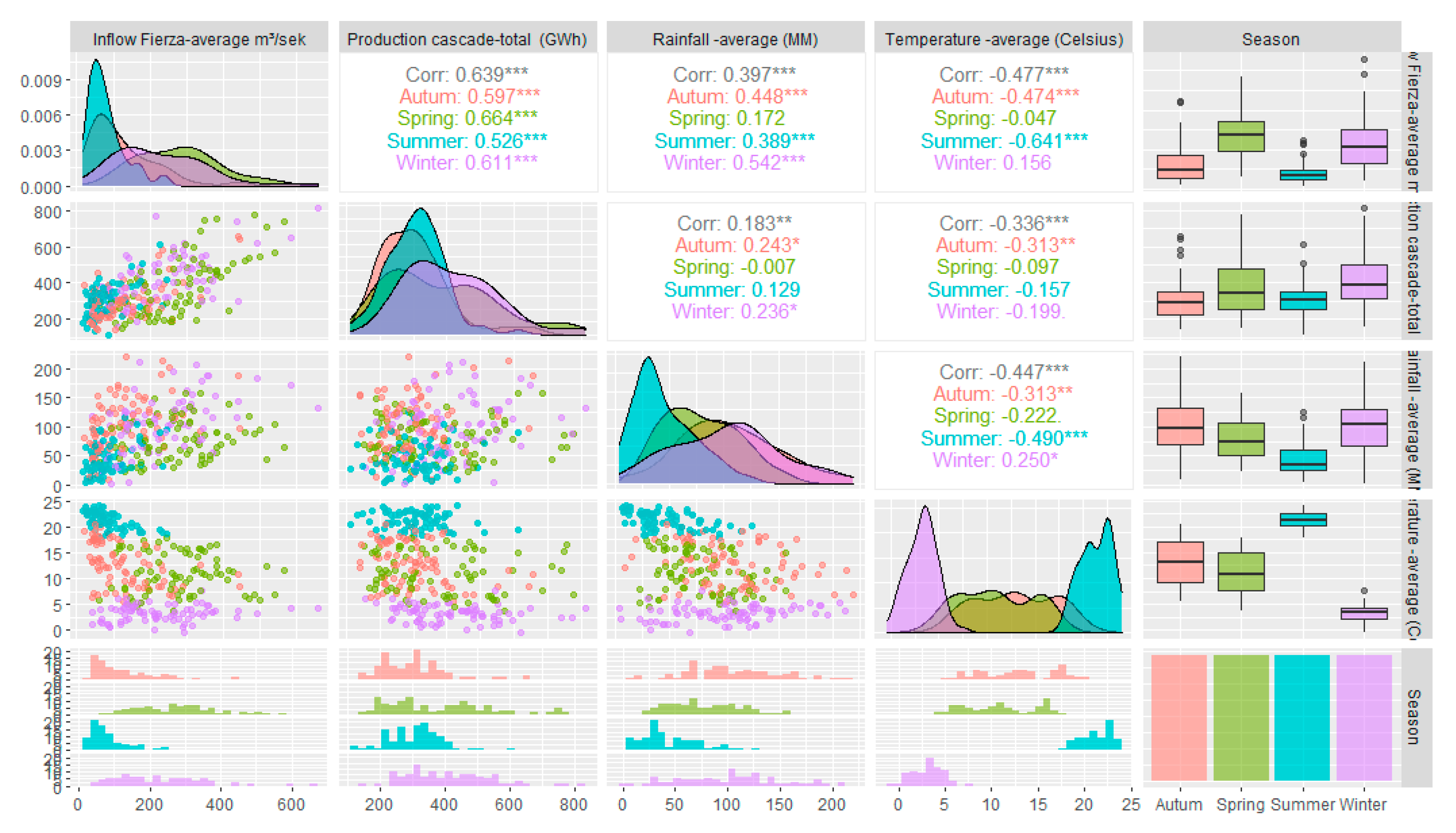
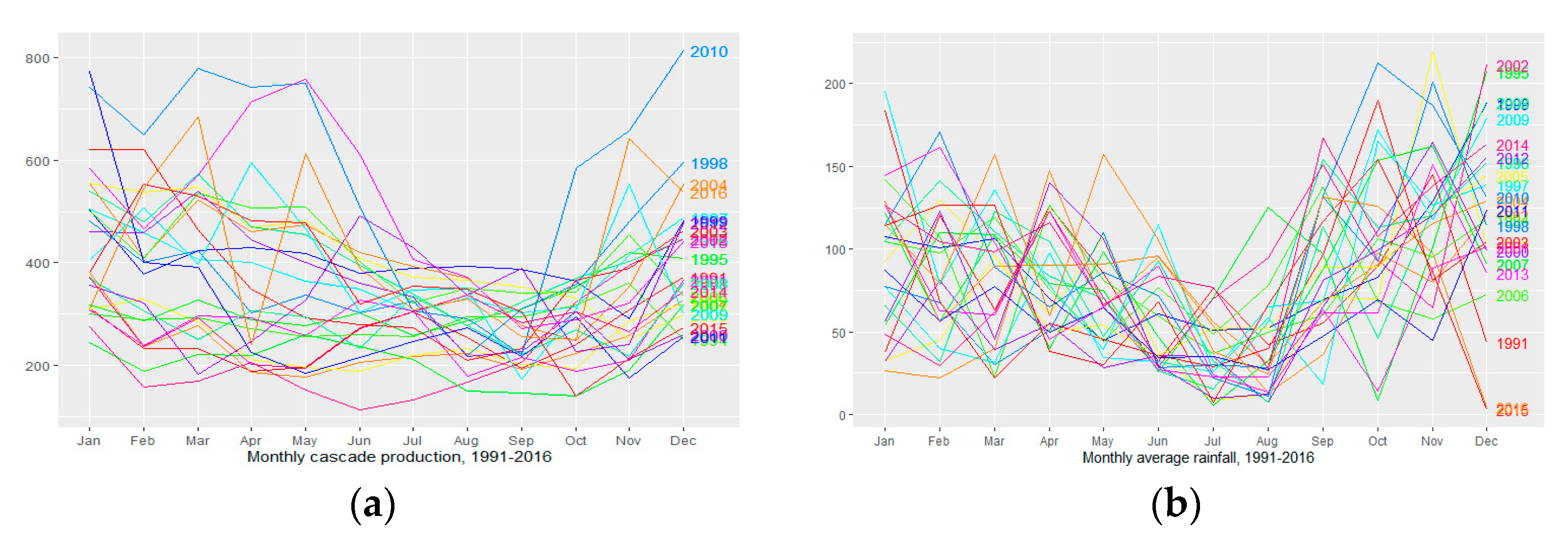
4. Results
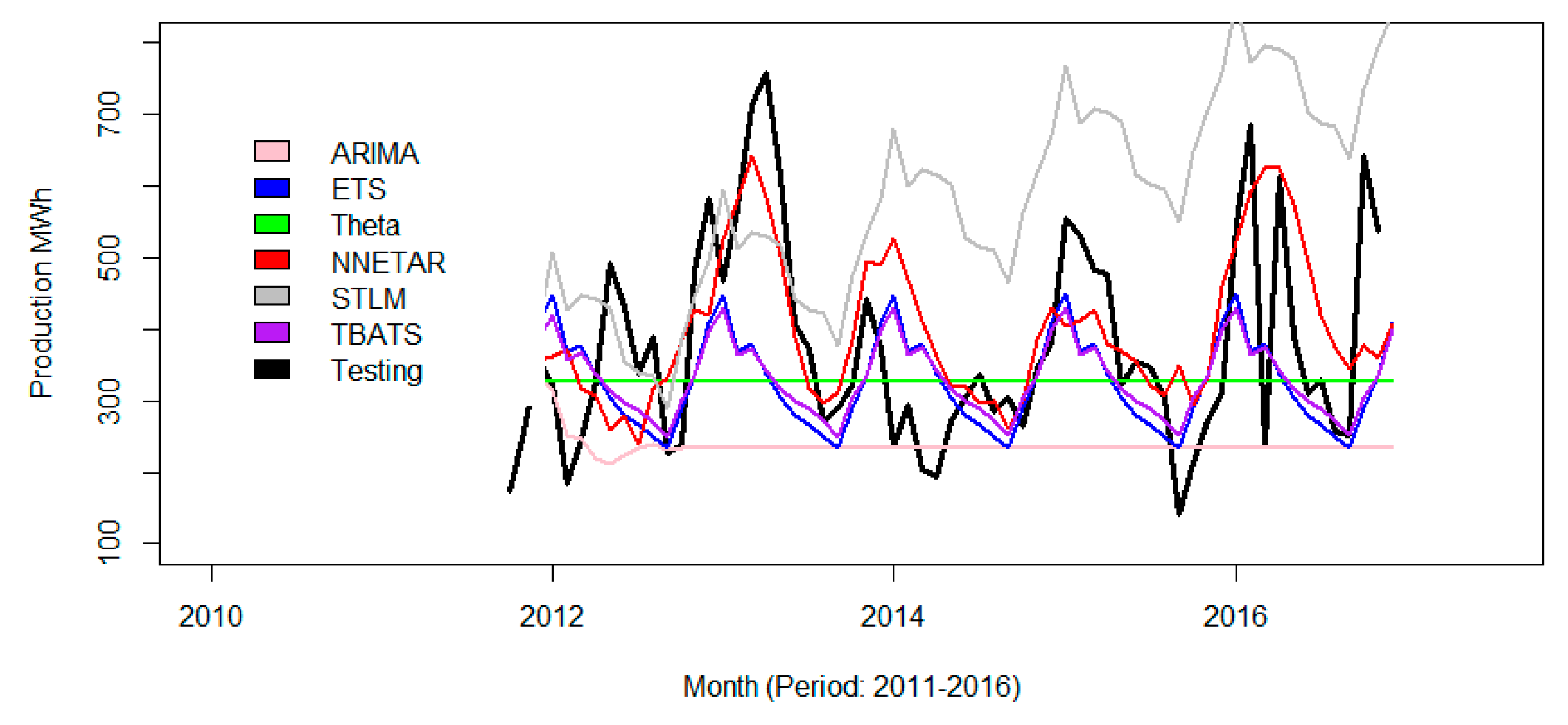
4.1. Models
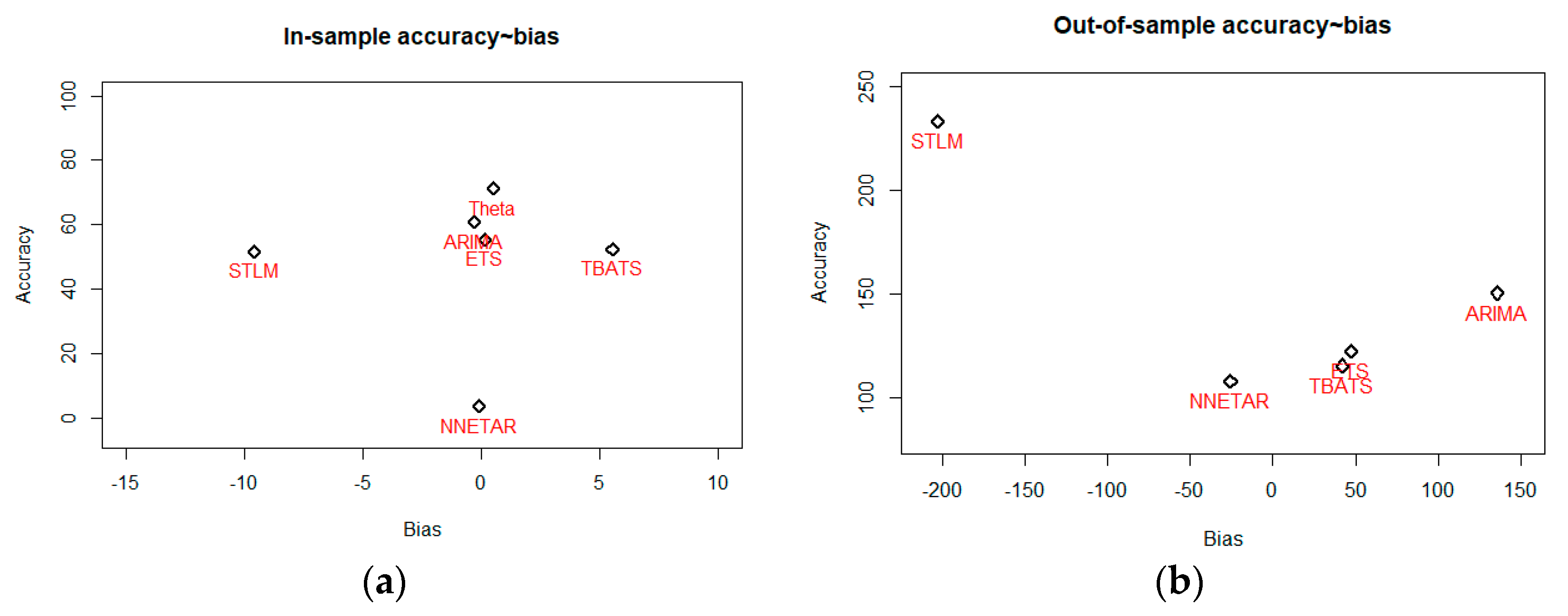
4.2. Model Performance Measures
5. Conclusions
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
References
- European Environment Agency (EEA). Report 2005. Available online: https://www.eea.europa.eu/publications/report_2005_0802_115659/at_download/file (accessed on 28 November 2020).
- KESH Albania. Available online: http://www.kesh.al/en/asset/drini-cascade/ (accessed on 28 November 2020).
- Available online: https://pressroom.ifc.org/all/pages/PressDetail.aspx?ID=26083 (accessed on 5 December 2020).
- Available online: https://crossbowproject.eu (accessed on 15 January 2021).
- Available online: https://adviser.albaniaenergy.org/wp-content/uploads/2018/11/Albania-hydroelectric-sector-towards-large-and-sustainable-developments-kept-by-Dr-Lorenc-Gordani.pdf (accessed on 15 January 2021).
- Martz, F.; Vuosku, J.; Ovaskainen, A.; Stark, S.; Rautio, P. The Snow Must Goon: Ground Ice Encasement, Snow Compaction and Absence of Snow Differently Cause Soil Hypoxia, CO2 Accumulation and Tree Seedling Damagein Boreal Forest. PLoS ONE 2016, 11, e0156620. [Google Scholar] [CrossRef]
- Confortola, G.; Soncini, A.; Bocchiola, D. Climate change will affect hydrological regimes in the Alps. J. Alp. Res. Rev. Géogr. Alp. 2013, 101–103. [Google Scholar] [CrossRef][Green Version]
- Saberian, A.; Hizam, H.; Radzi, M.A.M.; AbKadir, M.Z.A.; Mirzaei, M. Modelling and Prediction of Photovoltaic Power Output Using Artificial Neural Networks. Int. J. Photoenergy 2014, 2014, 469701. [Google Scholar] [CrossRef]
- Blöschl, G.; Hall, J.; Parajka, J.; Perdigão, R.A.; Merz, B.; Arheimer, B.; Aronica, G.T.; Bilibashi, A.; Bonacci, O.; Borga, M.; et al. Climate Change Shifts the Timing of European Floods. Sci. News Science 2017, 357, 588–590. [Google Scholar] [CrossRef]
- Blöschl, G.; Hall, J.; Viglione, A.; Perdigão, R.A.; Parajka, J.; Merz, B.; Lun, D.; Arheimer, B.; Aronica, G.T.; Bilibashi, A.; et al. Changing climate both increases and decreases European river floods. Nature 2019, 573, 108–111. [Google Scholar] [CrossRef]
- Wagner, T.; Themeßl, M.; Schüppel, A.; Gobiet, A.; Stigler, H.; Birk, S. Impacts of climate change on stream flow and hydropower generation in the Alpineregion. Env. Earth Sci. 2017, 76, 1–22. [Google Scholar] [CrossRef]
- Engeland, K.; Borga, M.; Creutin, J.D.; François, B.; Ramos, M.H.; Vidal, J.P. Space-time variability of climate variables and intermittent renewable electricity production—A review. Renew. Sustain. Energy Rev. 2017, 79, 600–617. [Google Scholar] [CrossRef]
- Schaeffer, R.; Szklo, A.S.; de Lucena, A.F.; Borba, B.S.; Nogueira, L.P.; Fleming, F.P.; Troccoli, A.; Harrison, M.; Boulahya, M.S. Energy sector vulnerability to climate change: A review. Energy 2012, 38, 1–12. [Google Scholar] [CrossRef]
- Chandramowli, S.N.; Felder, F.A. Impact of climate change on electricity systems and markets—A review of models and forecasts. Sustain. Energy Technol. Assess 2014, 5, 62–74. [Google Scholar] [CrossRef]
- Sun, T.; Zhang, T.; Teng, Y.; Chen, Z.; Fang, J. Monthly Electricity Consumption Forecasting Method Based on X12 and STL Decomposition Model in an Integrated Energy System. Math. Prob. Eng. 2019, 2019, 9012543. [Google Scholar] [CrossRef]
- Usha, T.; Balamurugan, S. Seasonal Based Electricity Demand Forecasting Using Time Series Analysis. Circuits Syst. 2016, 7, 3320–3328. [Google Scholar] [CrossRef]
- Kalimoldayev, M.; Drozdenko, A.; Koplyk, I.; Marinich, T.; Ab-dildayeva, A.; Zhukabayeva, T. Analysis of modern approaches for the prediction of electric energy consumption. Open Eng. 2020, 10, 350–361. [Google Scholar] [CrossRef]
- Crochet, P.; Jóhannesson, T.; Jónsson, T.; Sigurðsson, O.; Björnsson, H.; Pálsson, F.; Barstad, I. Estimating the Spatial Distribution of Precipitation in Iceland Usinga Linear Model of Orographic Precipitation. J. Hydrometeorol. 2007, 8, 1285–1306. [Google Scholar] [CrossRef]
- Gjika, E.; Ferrja, A.; Kamberi, A. A Study on the Efficiency of Hybrid Models in Forecasting Precipitations and Water Inflow Albania Case Study. Adv. Sci. Technol. Eng. Syst. J. 2019, 4, 302–310. [Google Scholar] [CrossRef]
- Box, G.E.; Hunter, W.H.; Hunter, S. Statistics for Experimenters; John Wiley and Sons: New York, NY, USA, 1978; Volume 664. [Google Scholar]
- Hyndman, R.; Koehler, A.B.; Ord, J.K.; Snyder, R.D. Forecasting with Exponential Smoothing: The State Space Approach; Springer Science & Business Media: Secaucus, NJ, USA, 2008. [Google Scholar]
- Makridakis, S.; Hibon, M. The M3-Competition: Results, conclusions and implications. Int. J. Forecast. 2000, 16, 451–476. [Google Scholar] [CrossRef]
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. The M4 competition: Results, findings, conclusion and way forward. Int. J. Forecast. 2018, 34, 802–808. [Google Scholar] [CrossRef]
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. Statistical and machine learning forecasting methods: Concern and ways forward. PLoS ONE 2018, 13, e0194889. [Google Scholar] [CrossRef] [PubMed]
- Bandara, K.; Bergmeir, C.; Smyl, S. Forecasting across time series databases using recurrent neural networks on groups of similar series: A clustering approach. Expert Syst. Appl. 2020, 140, 112896. [Google Scholar] [CrossRef]
- Hewamalage, H.; Bergmeir, C.; Bandara, K. Recurrent Neural Networks for Time Series Forecasting: Current status and future directions. Int. J. Forecast. 2021, 37, 388–427. [Google Scholar] [CrossRef]
- Del Angel, R.G. Financial time series forecasting using Artificial Neural Networks. Rev. Mex. Econ. Finanz. Nueva Época 2020, 15, 105–122. [Google Scholar]
- Tealab, A. Time series forecasting using artificial neural networks methodologies: Asystematic review. Future Comput. Inform. J. 2018, 3, 334–340. [Google Scholar] [CrossRef]
- Wang, L.; Zou, H.; Su, J.; Li, L.; Chaudhry, S. An ARIMA-ANN hybrid model for time series forecasting. Syst. Res. Behav. Sci. 2014, 30, 244–259. [Google Scholar] [CrossRef]
- Young, C.C.; Liu, W.C.; Hsieh, W.L. Predicting the water level fluctuation in an alpine lake using physically based, artificial neural network, and time series forecasting models. Math. Probl. Eng. 2015, 2015, 708204. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Khandakar, Y. Automatic Time Series Forecasting: The Forecast Package for R. J. Stat. Softw. 2008, 27, 1–22. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Hyndman, R.J. Measuring Forecast Accuracy. 2014. Available online: https://pdfs.semanticscholar.org/af71/3d815a7caba8dff7248ecea05a5956b2a487.pdf (accessed on 28 November 2020).
- Spiliotis, E.; Petropoulos, F.; Assimakopoulos, V. Improving the forecasting performance of temporal hierarchies. PLoS ONE 2019, 14, e0223422. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gjika, E.; Basha, L.; Ferrja, A.; Kamberi, A. Analyzing Seasonality in Hydropower Plants Energy Production and External Variables. Eng. Proc. 2021, 5, 15. https://doi.org/10.3390/engproc2021005015
Gjika E, Basha L, Ferrja A, Kamberi A. Analyzing Seasonality in Hydropower Plants Energy Production and External Variables. Engineering Proceedings. 2021; 5(1):15. https://doi.org/10.3390/engproc2021005015
Chicago/Turabian StyleGjika, Eralda, Lule Basha, Aurora Ferrja, and Arbesa Kamberi. 2021. "Analyzing Seasonality in Hydropower Plants Energy Production and External Variables" Engineering Proceedings 5, no. 1: 15. https://doi.org/10.3390/engproc2021005015
APA StyleGjika, E., Basha, L., Ferrja, A., & Kamberi, A. (2021). Analyzing Seasonality in Hydropower Plants Energy Production and External Variables. Engineering Proceedings, 5(1), 15. https://doi.org/10.3390/engproc2021005015





