Sensitivity Analysis of Internally Reinforced Beam-Subjected Torsion Loading †
Abstract
:1. Introduction
2. Numerical Procedure
3. Results and Discussion
4. Conclusions
- It is evident that the geometric variables VA1, VA2, and VA3 have been appropriately chosen for the optimization technique.
- The findings suggest that the deflections of the finite element method (FEM) model exhibit a high degree of sensitivity to the elements indicated earlier.
- The models demonstrate geometric restrictions, particularly with respect to their interior arrangement. To avoid the interference of structural elements from the sides or top/bottom, it is necessary for the variables VA1 and VA2 to possess a significant magnitude, hence enabling the continuation of optimization analyses without hindrance.
- The approach followed mitigates the inability to identify the most ideal solution.
- It is imperative that the size of the parameter remains within a modest range to facilitate the development of lightweight components that align with the specific aims of the study. Simultaneously, it should be sufficiently high to avoid substantial nonlinear effects in any future practical applications.
- Prior studies have established that the utilization of parameterization in the ANSYS input file is a viable approach for assessing the system’s responsiveness to the design factors under investigation. This has implications on practical applications, considering that the behavior of the manufactured structure, if properly optimized, is much better than if the optimization setup is not the best, i.e., does not lead to the best results, according to the objective. Therefore, the results obtained from the sensitivity analysis have the potential to inform future decision-making processes in the determination of variable weights for optimization techniques and procedures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Silva, H.M. Determination of Material/Geometry of the Section Most Adequate for a Static Loaded Beam Subjected to a Combination of Bending and Torsion. Master’s Thesis, University of Minho, Guimaraes, Portugal, 2011. [Google Scholar]
- Silva, H.M.; Meireles, J.F. Determination of material/geometry of the section most adequate for a static loaded beam subjected to a combination of bending and torsion. Mater. Sci. Forum 2013, 730–732, 507–512. [Google Scholar] [CrossRef]
- Silva, H.M.; Meireles, J.F. Feasibility of internally reinforced thin-walled beams for industrial applications. Appl. Mech. Mater. 2015, 775, 119–124. [Google Scholar] [CrossRef]
- Silva, H.M.; Meireles, J.F. Structural Optimization of internally reinforced beams subjected to uncoupled and coupled bending and torsion loads for industrial applications-Accepted for publication n in the journal Mechanics and Mechanical Engineering. Mech. Mech. Eng. 2017, 21, 731–753. [Google Scholar]
- Orlov, P. Fundamentals of Machine Design, 1st ed.; MIR Publishers: Moscow, Russia, 1976. [Google Scholar]
- Vieira, D.G.; Meireles, J.F.; Nunes, J.P. Improving the Dynamical Behavior of a Laser Cutting Equipment by Using a Carbon. Mater. Sci. Forum 2013, 730, 349–354. [Google Scholar]
- Weckman, R. Diagonal ribs increase torsional rigidity. 1988. Available online: https://www.scribd.com/doc/98726339/DCI388 (accessed on 1 November 2023).
- Liu, Y. Design enhancement of thin-walled steel beams with improved stiffness and reduced weight. Int. J. Des. Eng. 2008, 1, 149–165. [Google Scholar] [CrossRef]
- Liu, Y.; Gannon, L. Finite element study of steel beams reinforced while under load. Eng. Struct. 2009, 31, 2630–2642. [Google Scholar] [CrossRef]
- Szewczak, R.; Smith, E.; DeWolf, J. Beams with Torsional Stiffeners. J. Struct. Eng. 1983, 109, 1635–1647. [Google Scholar] [CrossRef]
- Heins, C.P., Jr.; Potocko, R.A. Torsional Stiffening of I-Girder Webs. J. Struct. Div. 1979, 105, 1689–1698. [Google Scholar] [CrossRef]
- Silva, H.M. Optimization of the Mechanical Behavior of Hollow-Box Beams. Ph.D. Thesis, Lodz University of Technology, Łódź, Poland, 2018. [Google Scholar]
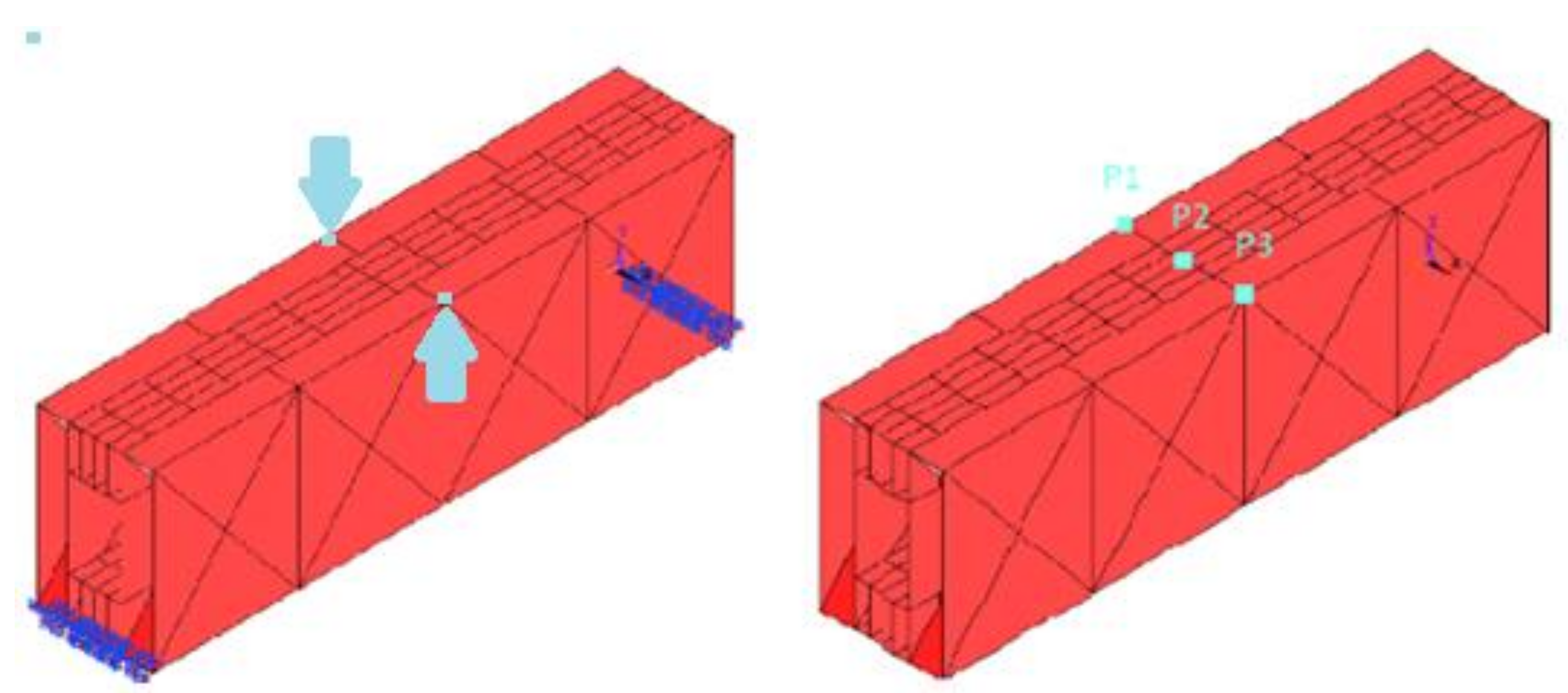

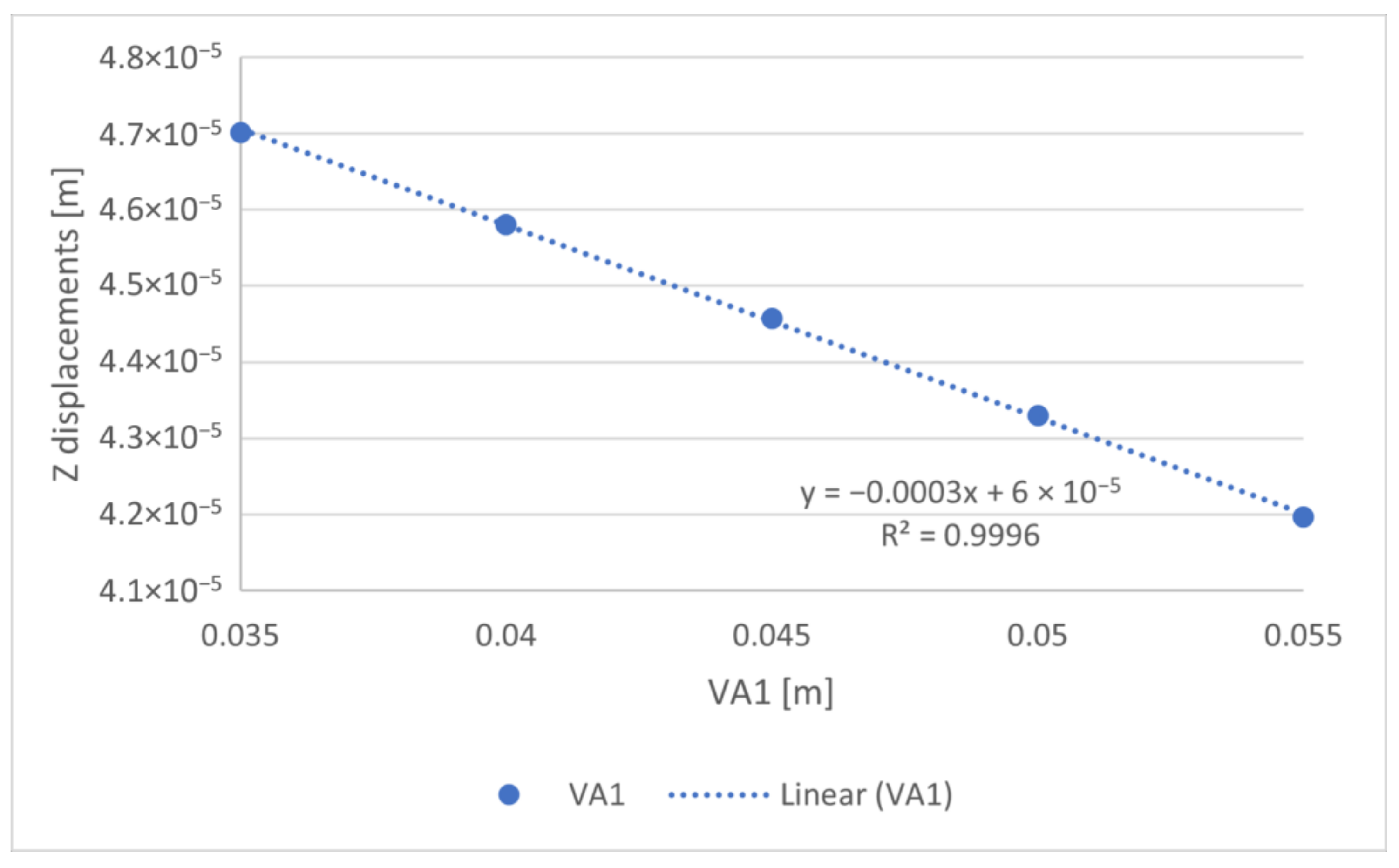

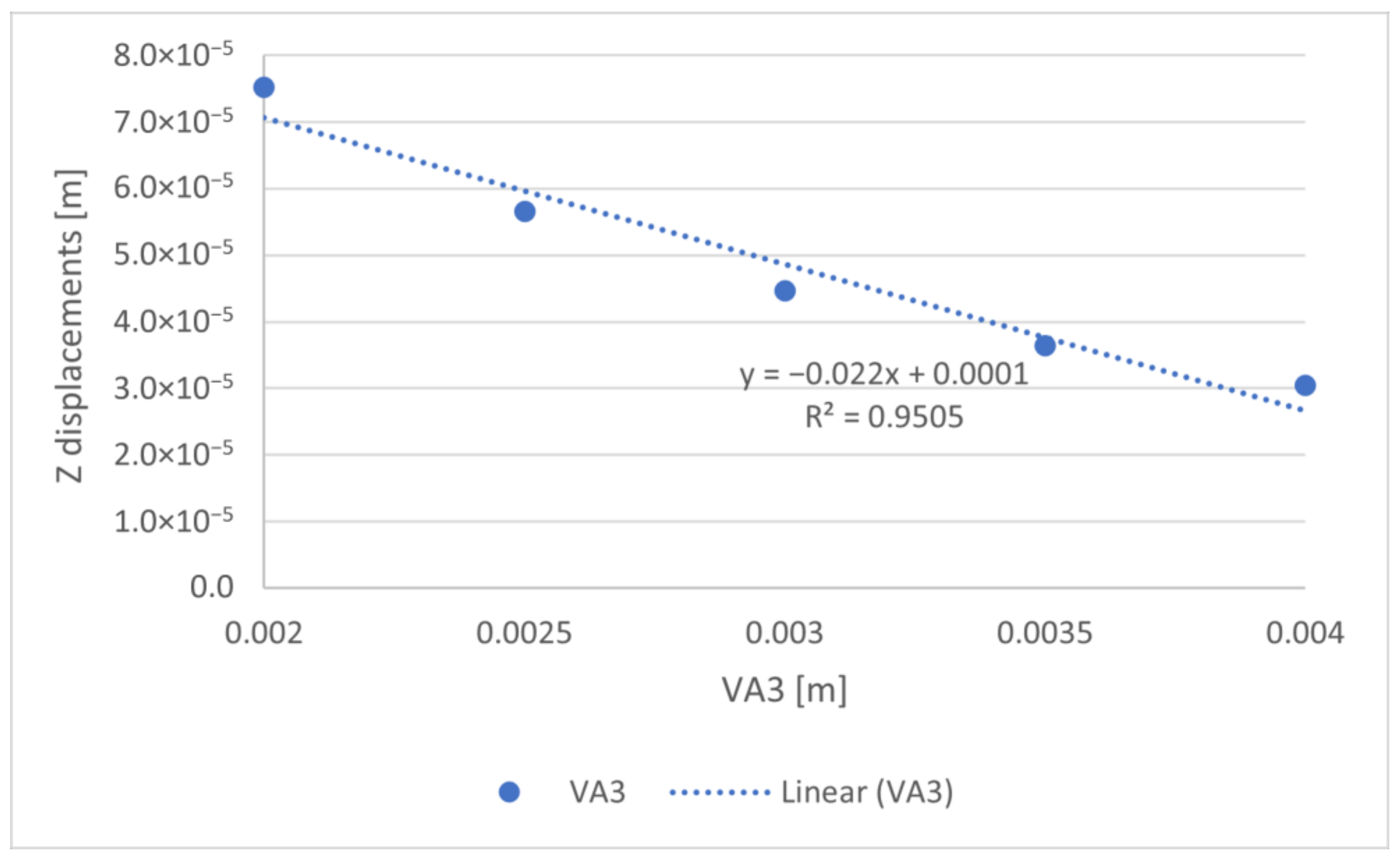
| Coefficient | ||||
|---|---|---|---|---|
| Variable | Type | m | b | R2 |
| VA1 | Linear, dz = m × VAx + b where x = 1,2,3. | −3 × 10−4 | 6 × 10−5 | 0.9996 |
| VA2 | 3 × 10−5 | 4 × 10−5 | 0.9974 | |
| VA3 | −2.2 × 10−2 | 1 × 10−4 | 0.9505 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva, H.M.; Wojewoda, J. Sensitivity Analysis of Internally Reinforced Beam-Subjected Torsion Loading. Eng. Proc. 2023, 56, 284. https://doi.org/10.3390/ASEC2023-15815
Silva HM, Wojewoda J. Sensitivity Analysis of Internally Reinforced Beam-Subjected Torsion Loading. Engineering Proceedings. 2023; 56(1):284. https://doi.org/10.3390/ASEC2023-15815
Chicago/Turabian StyleSilva, Hugo Miguel, and Jerzy Wojewoda. 2023. "Sensitivity Analysis of Internally Reinforced Beam-Subjected Torsion Loading" Engineering Proceedings 56, no. 1: 284. https://doi.org/10.3390/ASEC2023-15815
APA StyleSilva, H. M., & Wojewoda, J. (2023). Sensitivity Analysis of Internally Reinforced Beam-Subjected Torsion Loading. Engineering Proceedings, 56(1), 284. https://doi.org/10.3390/ASEC2023-15815







