Observer Design for Takagi–Sugeno Fuzzy Systems with Unmeasurable Premise Variables Based on Differential Mean Value Theorem ^†

Abstract

In this work, we present the design of an observer for Takagi–Sugeno fuzzy systems with unmeasurable premise variables. Moving away from Lipschitz-based and ${\mathcal{L}}_2$ attenuation-based methods—which fall short in eliminating the mismatching terms in the estimation error dynamics—we leverage the differential mean value theorem. This approach not only removes these terms but also streamlines the factorization of the estimation error dynamics, making it directly proportional to the estimation error. To ensure the asymptotic convergence of the estimation error, we apply the second Lyapunov theorem, which provides sufficient stability conditions described as linear matrix inequalities. A numerical example applied on a three-tank hydraulic system is presented to demonstrate the observer’s effectiveness.

1. Introduction

In the industrial sector, cost-effectiveness is paramount. A key strategy to achieve this is using observers to reduce the need for expensive sensors. The Luenberger observer [1] has paved the way for numerous advancements. Takagi–Sugeno (TS) fuzzy systems, which represent nonlinear systems as a weighted sum of linear ones [2], have provided valuable tools for understanding complex dynamics. Using the sector nonlinearity approach, these systems can be accurately described [3]. Based on variables in their weight functions, they’re classified into measurable premise variables (MPV) and unmeasurable premise variables (UPVs), with the latter being a primary research focus because it represents the largest category of systems.

Designing observers for systems equipped with UPV tends to be more intricate than their measurable counterparts. These complexities stem predominantly from the mismatching terms in the error dynamics. To address such hurdles, the scientific community has forwarded various techniques. Initially, the Lipschitz-based method emerges as a straightforward solution [4,5], yet stumbles when the nonlinear system’s Lipschitz constant exceeds an admissible value, thereby introducing pronounced conservatism in Linear Matrix Inequality (LMI) constraints. An alternative, the ${\mathcal{L}}_2$-attenuation-based approach [6,7], focuses on minimizing the aforementioned mismatches. Though typically less conservative than the Lipschitz method, there remain instances where the attenuation level is not minimal enough to be accepted, even if the simulation works. This paves the way for the mean value theorem (MVT) method [8,9], allowing the factorization of the estimation error dynamics, which leads to making it proportional completely to the estimation error. Hence, the mismatching terms disappeared from the estimation error dynamics.

The observer based on the MVT, leading to an exact transformation of error dynamics into an LPV system, was introduced in [10]. Subsequent works, such as [11,12], represent dynamic error using TS representation. This theorem’s applications span various studies: real-time motor control in [13], robust $H_{\infty }$ control for motors in [14], sensorless control for a PMSM in [15], and automotive slip angle estimation in [12]. A notable advancement is in [16], where line integral Lyapunov functions reduce conservatism in MVT observers.

In this paper, we introduce an observer design based on the mean value theorem and validate its efficacy via a simulation on a three-tank hydraulic system. The paper’s structure is as follows: Section 2 delves into the TS fuzzy representation and the mean value theorem. Section 3 details the observer design, Section 4 showcases the simulation results, and Section 5 concludes with potential directions for future research.

2. Preliminaries

2.1. Takagi–Sugeno Fuzzy Representation

Let us consider the following nonlinear system:

$$\left\{\begin{array}{c}\dot{\mathrm{x}}\left(\mathrm{t}\right)=f(x\left(t\right),u\left(t\right))\hfill \\ \mathrm{y}\left(\mathrm{t}\right)=\mathrm{g}\left(\mathrm{x}\right(\mathrm{t}\left)\right)\hfill \end{array}\right.$$

(1)

where $x\left(t\right)\in {\mathbb{R}}^n$ is the state vector, $u\left(t\right)\in {\mathbb{R}}^{n_u}$ is the input vector, and $y\left(t\right)\in {\mathbb{R}}^{n_y}$ represents the output vector.

The TS model reformulates the nonlinear system (1) using a convex combination of linear sub-models. Each $i^{th}$ sub-model follows the given fuzzy rule:

$$\mathrm{If}{\xi }_1\mathrm{is}{M}_{i1}\mathrm{and}\dots \mathrm{and}{\xi }_{\mathrm{l}}\mathrm{is}{M}_{i\mathrm{l}}\mathrm{Then}:\left\{\begin{array}{c}\dot{\mathrm{x}}\left(\mathrm{t}\right)={\mathrm{A}}_{\mathrm{i}}\mathrm{x}\left(\mathrm{t}\right)+{\mathrm{B}}_{\mathrm{i}}\mathrm{u}\left(\mathrm{t}\right)\hfill \\ \mathrm{y}\left(\mathrm{t}\right)={\mathrm{C}}_i\mathrm{x}\left(\mathrm{t}\right)\hfill \end{array}\right.$$

(2)

where $\xi$ is premise variable, l is the number of premise variables, and $M_{ij}$ is the membership function of the $i^{th}$ fuzzy rule corresponding to the $j^{th}$ premise variable. $A_i\in {\mathbb{R}}^{n\times n},B_i\in {\mathbb{R}}^{n\times n_u},$ and $C_i\in {\mathbb{R}}^{n_y\times n}$ are known matrices.

The global TS fuzzy representation of the nonlinear system (1) is described as follows:

$$\left\{\begin{array}{c}\dot{\mathrm{x}}\left(\mathrm{t}\right)=\sum _{\mathrm{i}=1}^{\mathrm{r}}{\mu }_{\mathrm{i}}\left(\mathrm{x}\left(\mathrm{t}\right)\right)\left({\mathrm{A}}_{\mathrm{i}}\mathrm{x}\left(\mathrm{t}\right)+{\mathrm{B}}_{\mathrm{i}}\mathrm{u}\left(\mathrm{t}\right)\right)\hfill \\ \mathrm{y}\left(\mathrm{t}\right)=\sum _{\mathrm{i}=1}^{\mathrm{r}}{\mu }_{\mathrm{i}}\left(\mathrm{x}\left(\mathrm{t}\right)\right){\mathrm{C}}_i\mathrm{x}\left(\mathrm{t}\right)\hfill \end{array}\right.$$

(3)

where ${\mu }_i\left(x\left(t\right)\right)$ is the weighting functions described by ${\mu }_i\left(x\left(t\right)\right)={\prod }_{j=1}^l{M}_{ij}\left({\xi }_j\right)$ and verifies the convex sum property ${\sum }_{\mathrm{i}=1}^{\mathrm{r}}{\mu }_{\mathrm{i}}\left(\mathrm{x}\left(\mathrm{t}\right)\right)=1,0\le {\mu }_{\mathrm{i}}\left(\mathrm{x}\left(\mathrm{t}\right)\right)\le 1,\forall \mathrm{i}=1,\dots \mathrm{r}$.

2.2. Differential Mean Value Theorem [10]

Let $\Phi \left(x\right):R^n=>R^n$ be a differentiable vector function described as follows:

$$\Phi \left(x\right)=\sum _{i=1}^n{e}_n\left(i\right){\Phi }_i\left(x\right)$$

(4)

where the set $E_n$ is the canonical basis of the vectorial space ${\mathbb{R}}^n$ for all $n\ge 1$ given by:

$$E_n=\left\{e_n\left(i\right)\right|e_n\left(i\right)={(0,...,0,\underset{\mathrm{i}}{\underbrace{1}},0,...,0)}^T,i=1,...,n\}$$

(5)

Let $a,b\in {\mathbb{R}}^n$. Then, there are constant vectors $z_1,...,z_n\in (a,b),z_i\ne a,z_i\ne b$ for $i=1,...,n$ such that the mean value theorem ensures the following relation:

$$\Phi \left(a\right)-\Phi \left(b\right)=\sum _{i=1}^n\sum _{j=1}^n{e}_n\left(i\right){e_n\left(j\right)}^T\frac{\partial {\Phi }_i\left(z_j\right)}{\partial x_j}\left(a-b\right)$$

(6)

Applying sector nonlinearity allows for rewriting the above equation using TS transformation:

$$\Phi \left(a\right)-\Phi \left(b\right)=\sum _{i=1}^{s\le 2^{n^2}}{h}_i\left(z\left(t\right)\right){\mathcal{H}}_i\left(a-b\right)$$

(7)

where ${\mathcal{H}}_i$ represents the sub-models of the nonlinear term ${\sum }_{i=1}^n{\sum }_{j=1}^n{e}_n\left(i\right)e_n{\left(j\right)}^T\frac{\partial {\Phi }_i\left(z_j\right)}{\partial x_j}$, and $h_i\left(z\left(t\right)\right)$ is its weighting function.

3. Mean Value Theorem Observer-Based Design

Let us consider the following observer for fuzzy system (3):

$$\left\{\begin{array}{c}\dot{\widehat{\mathrm{x}}}\left(\mathrm{t}\right)=\sum _{\mathrm{i}=1}^{\mathrm{r}}{\mu }_{\mathrm{i}}\left(\widehat{\mathrm{x}}\left(\mathrm{t}\right)\right)\left({\mathrm{A}}_{\mathrm{i}}\widehat{\mathrm{x}}\left(\mathrm{t}\right)+{\mathrm{B}}_{\mathrm{i}}\mathrm{u}\left(\mathrm{t}\right)\right)+\mathrm{L}(\mathrm{y}\left(\mathrm{t}\right)-\widehat{\mathrm{y}}\left(\mathrm{t}\right))\hfill \\ \mathrm{y}\left(\mathrm{t}\right)=\sum _{\mathrm{i}=1}^{\mathrm{r}}{\mu }_{\mathrm{i}}\left(\widehat{\mathrm{x}}\left(\mathrm{t}\right)\right){\mathrm{C}}_{\mathrm{i}}\widehat{\mathrm{x}}\left(\mathrm{t}\right)\hfill \end{array}\right.$$

(8)

The following theorem provides sufficient conditions described as LMI to ensure the asymptotic convergence of the error dynamic:

Theorem 1.

The estimation error converges asymptotically toward zero with decay rate α if there exist matrices $P=P^T\in {\mathbb{R}}^{n_x\times n_x}>0$ and $M\in {\mathbb{R}}^{n_x\times n_y}$ such that the following LMI holds $\forall i=1,...,q$:

$${\mathcal{A}}_{\mathrm{i}}{}^{T}P+P{\mathcal{A}}_{\mathrm{i}}-M{\mathcal{C}}_i-{\mathcal{C}}_i{}^T{M}^T+2\alpha P<0$$

(9)

The observer gain is given by $L=P^{-1}M$.

Proof. 

The dynamics of the estimation error $e\left(t\right)=x\left(t\right)-\widehat{x}\left(t\right)$ are given as follows:

$$\dot{\mathrm{e}}\left(\mathrm{t}\right)=\underset{{\Phi }_1\left(\mathrm{x}\left(t\right)\right)}{\underbrace{\sum _{\mathrm{i}=1}^{\mathrm{r}}{\mu }_{\mathrm{i}}\left(\mathrm{x}\left(\mathrm{t}\right)\right)\left({\mathrm{A}}_{\mathrm{i}}x\left(\mathrm{t}\right)+{\mathrm{B}}_{\mathrm{i}}\mathrm{u}\left(\mathrm{t}\right)\right)}}-\underset{{\Phi }_1\left(\widehat{x}\left(t\right)\right)}{\underbrace{\sum _{\mathrm{i}=1}^{\mathrm{r}}{\mu }_{\mathrm{i}}\left(\widehat{\mathrm{x}}\left(\mathrm{t}\right)\right)\left({\mathrm{A}}_{\mathrm{i}}\widehat{\mathrm{x}}\left(\mathrm{t}\right)+{\mathrm{B}}_{\mathrm{i}}\mathrm{u}\left(\mathrm{t}\right)\right)}}-\mathrm{L}(\underset{{\Phi }_2\left(\mathrm{x}\left(t\right)\right)}{\underbrace{\sum _{\mathrm{i}=1}^{\mathrm{r}}{\mu }_{\mathrm{i}}\left(\mathrm{x}\left(\mathrm{t}\right)\right){\mathrm{C}}_i\mathrm{x}\left(\mathrm{t}\right)}}-\underset{{\Phi }_2\left(\widehat{x}\left(t\right)\right)}{\underbrace{\sum _{\mathrm{i}=1}^{\mathrm{r}}{\mu }_{\mathrm{i}}\left(\widehat{\mathrm{x}}\left(\mathrm{t}\right)\right){\mathrm{C}}_{\mathrm{i}}\widehat{\mathrm{x}}\left(\mathrm{t}\right)}})$$

(10)

Using the mean value theorem on the terms ${\Phi }_1$ and ${\Phi }_2$, the error dynamics become the following:

$$\begin{array}{c}\dot{e}\left(t\right)=\sum _{i=1}^q{h}_i\left(z\left(t\right)\right)\left({\mathcal{A}}_i-L{\mathcal{C}}_i\right)e\left(t\right)\end{array}$$

(11)

To study the stability of the error dynamics, the quadratic Lyapunov function is used:

$$\begin{array}{c}V\left(t\right)={e\left(t\right)}^{T}Pe\left(t\right)\end{array}$$

(12)

The derivative of $V\left(t\right)$ with respect to t is as follows:

$$\dot{V}\left(t\right)=\sum _{i=1}^q{h}_i\left(z\left(t\right)\right)e^T\left({\left({\mathcal{A}}_i-L{\mathcal{C}}_i\right)}^{T}P+P\left({\mathcal{A}}_i-L{\mathcal{C}}_i\right)\right)e$$

(13)

To improve the performance of the estimation, the following decay rate is used:

$$\begin{array}{c}\dot{V}\left(t\right)\le -2\alpha V\left(t\right)\end{array}$$

(14)

By substituting (12) and (13) in (14), the following inequality is obtained:

$$\sum _{i=1}^q{h}_i\left(z\left(t\right)\right)e_a^T\left({\mathcal{A}}_{\mathrm{i}}^{T}P-{\mathcal{C}}_i^T{L}^{T}P+P{\mathcal{A}}_{\mathrm{i}}-PL{\mathcal{C}}_i+2\alpha P\right)e_a<0$$

(15)

The inequality (15) is not linear due to the product of the variables P and L. However, applying the change in variable $M=PL$ provides a solution for achieving the linear stability conditions outlined in Theorem 1. □

In order to solve the inequalities outlined in Theorem 1, we will utilize the Yalmip Toolbox, a well-regarded modeling language in MATLAB designed for formulating optimization problems. This toolbox seamlessly integrates with a variety of solvers, including “Mosek”, “SDPT3”, and “LMILAB”, all recognized for their efficiency in handling LMIs.

In Figure 1, the entire procedure is depicted through a graphical representation:

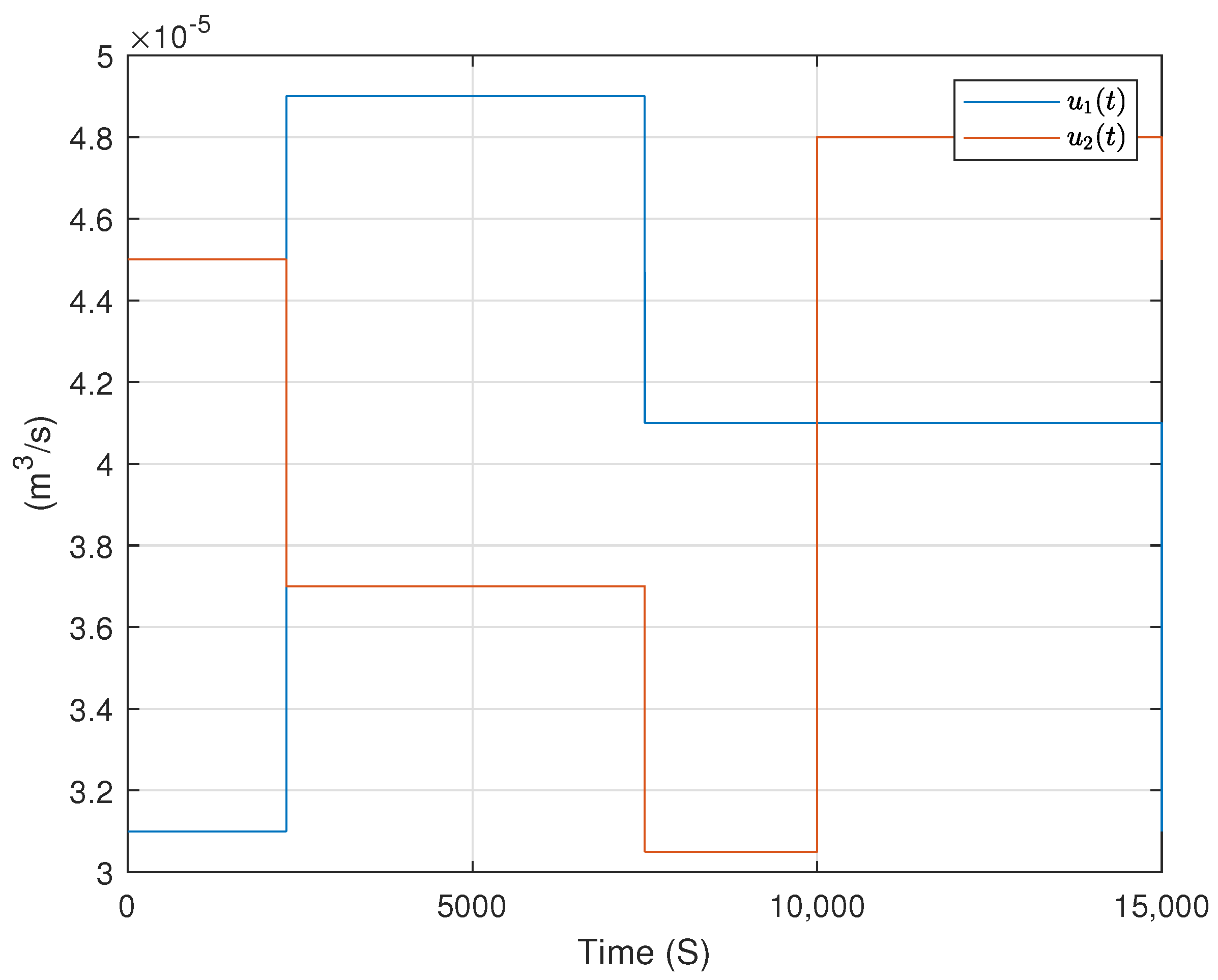
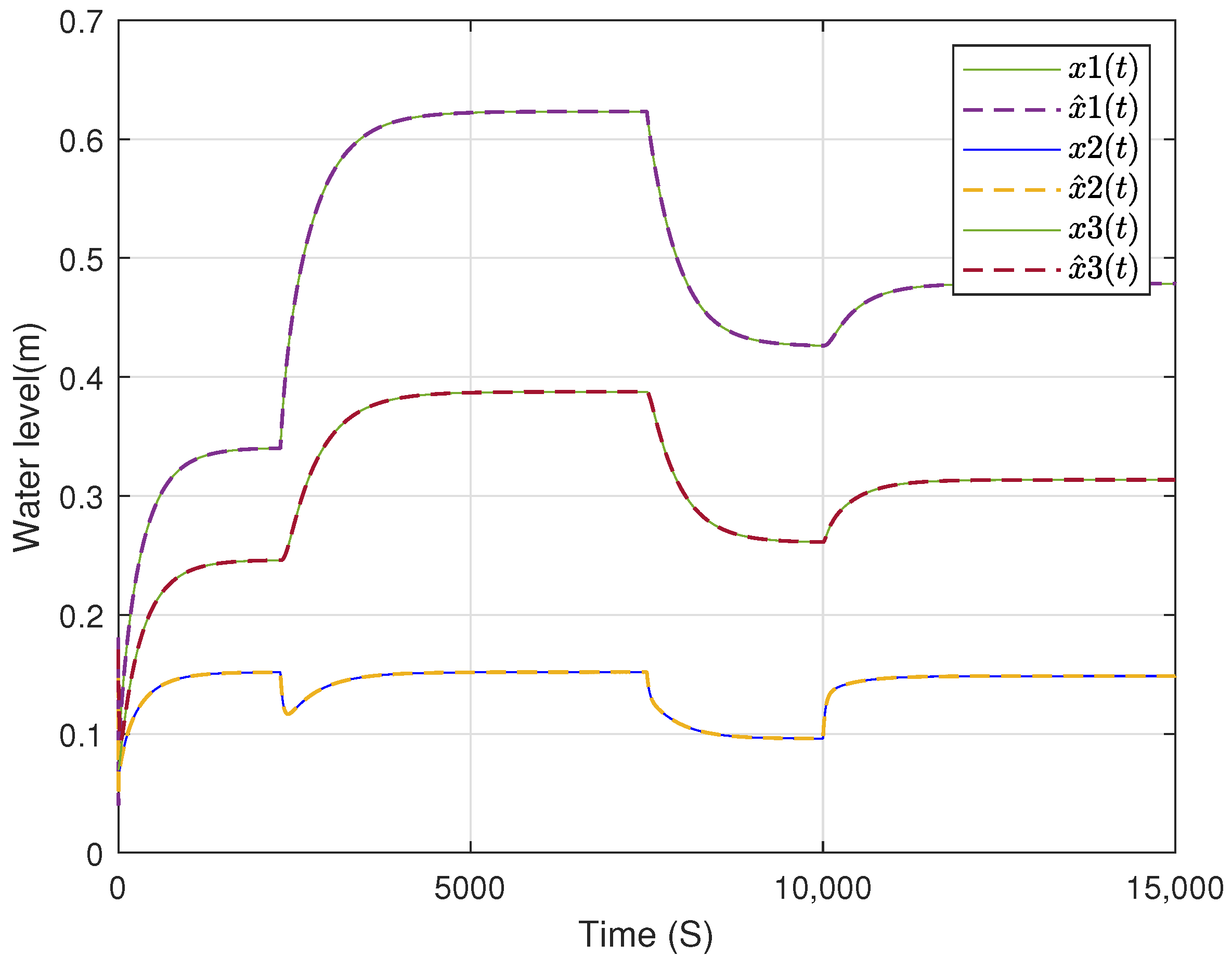
4. Simulation Results

4.1. Dynamic Model of the System

The three-tank hydraulic system illustrated in Figure 2, based on Guzman’s design [17], features three tanks with equal cross-sectional areas S, connected by pipes with areas $S_{p1,2,3}$. Water from a reservoir fills the first and second tanks via pumps $P_1$ and $P_2$, with flow rates $u_1$ and $u_2$. Valves in each tank manage water release, and the system ensures water levels in the order $x_1>x_3>x_2$.

Let us define $x\left(t\right)={\left[\begin{array}{ccc}{x}_1& x_2& x_3\end{array}\right]}^T,u\left(t\right)={\left[\begin{array}{cc}{u}_1& u_2\end{array}\right]}^T$ and the premise variables $\xi \left(x\right)={\left[\begin{array}{ccc}{\xi }_1\left(x\right)& {\xi }_2\left(x\right)& {\xi }_3\left(x\right)\end{array}\right]}^T$. Using these definitions, the system can be represented in the following state-space form:

$$\dot{x}\left(t\right)=\frac{1}{S}\left[\begin{array}{ccc}-C_1{\xi }_1\left(x\right)& 0& 0\\ 0& -C_2{\xi }_2\left(x\right)& C_3{\xi }_3\left(x\right)\\ C_1{\xi }_1\left(x\right)& 0& -C_3{\xi }_3\left(x\right)\end{array}\right]x\left(t\right)+\frac{1}{S}\left[\begin{array}{cc}1\hfill & 0\hfill \\ 0\hfill & 1\hfill \\ 0\hfill & 0\hfill \end{array}\right]u\left(t\right)$$

(16)

where

$${\xi }_1\left(x\right)=\frac{\sqrt{\left|x_1-x_3\right|}}{x_1},{\xi }_2\left(x\right)=\frac{\sqrt{x_2}}{x_2},{\xi }_3\left(x\right)=\frac{\sqrt{\left|x_3-x_2\right|}}{x_3}$$

$$C_1={\eta }_{13}.S_{p1}.sign\left(x_1-x_3\right).\sqrt{2g},C_2={\eta }_{20}.S_{p2}.\sqrt{2g},C_3={\eta }_{32}.S_{p3}.sign\left(x_3-x_2\right).\sqrt{2g}$$

With a gravitational pull of $g=9.8{\mathrm{m}/\mathrm{s}}^2$, the system has discharge coefficients ${\eta }_{13}={\eta }_{32}=0.456$ and ${\eta }_{20}=0.652$. The tubes’ cross-sectional areas are $S_{p1}=S_{p3}=0.5\times {10}^{-4}{\mathrm{m}}^2$ and $S_{p2}=0.8\times {10}^{-4}{\mathrm{m}}^2$, with all tanks having $S=154\times {10}^{-4}{\mathrm{m}}^2$. Given the constraint $x_1>x_3>x_2$ and these parameters, we derive $C_1=1.0094\times {10}^{-4}$, $C_2=2.3092\times {10}^{-4}$, and $C_3=1.0094\times {10}^{-4}$.

4.2. Observer Design for Three-Tank Hydraulic System

In order to apply Theorem 1, the matrices ${\mathcal{A}}_i$ and ${\mathcal{C}}_i$ have to be determined. According to the mean value theorem, ${\Phi }_1\left(\xi \right)$ and its Jacobian $\frac{\partial {\Phi }_1\left(\xi \right)}{\partial x}$ can be defined as follows:

$${\Phi }_1\left(\xi \right)=\frac{1}{S}\left[\begin{array}{c}-C_1{\xi }_1{x}_1\\ -C_2{\xi }_2{x}_2+C_3{\xi }_3{x}_3\\ C_1{\xi }_1{x}_1-C_3{\xi }_3{x}_3\end{array}\right]$$

$$\frac{\partial {\Phi }_1\left(\xi \right)}{\partial x}=\frac{1}{S}\left[\begin{array}{ccc}\frac{-C_1}{2}{\epsilon }_1\left(x\right)& 0& \frac{C_1}{2}{\epsilon }_1\left(x\right)\\ 0& \frac{-C_2}{2}{\epsilon }_2\left(x\right)-\frac{C_3}{2}{\epsilon }_3\left(x\right)& \frac{C_3}{2}{\epsilon }_3\left(x\right)\\ \frac{C_1}{2}{\epsilon }_1\left(x\right)& \frac{C_3}{2}{\epsilon }_3\left(x\right)& -\frac{C_3}{2}{\epsilon }_3\left(x\right)-\frac{C_1}{2}{\epsilon }_1\left(x\right)\end{array}\right]$$

where the new premise variables ${\epsilon }_i\left(x\right)$ are given by ${\epsilon }_1\left(x\right)=\frac{1}{\sqrt{x_1-x_3}};{\epsilon }_2\left(x\right)=\frac{1}{\sqrt{x_2}};{\epsilon }_3\left(x\right)=\frac{1}{\sqrt{x_3-x_2}}$ and the limits are $L_{\epsilon 1}\left(j\right)=\left[\begin{array}{cc}2& 12\end{array}\right]$, $L_{\epsilon 2}\left(k\right)=\left[\begin{array}{cc}2& 4\end{array}\right]$ and $L_{\epsilon 3}\left(d\right)=\left[\begin{array}{cc}2& 14\end{array}\right]$ for $j,k,d=1:2$.

By replacing every premise variable by its respective limits in a loop, the matrices ${\mathcal{A}}_i$ can be obtained as follows for $\left(i=1,\dots ,8\right)$:

$${\mathcal{A}}_i=\frac{1}{S}\left[\begin{array}{ccc}\frac{-C_1}{2}{L}_{\epsilon 1}\left(j\right)& 0& \frac{C_1}{2}{L}_{\epsilon 1}\left(j\right)\\ 0& \frac{-C_2}{2}{L}_{\epsilon 2}\left(k\right)-\frac{C_3}{2}{L}_{\epsilon 3}\left(d\right)& \frac{C_3}{2}{L}_{\epsilon 3}\left(d\right)\\ \frac{C_1}{2}{L}_{\epsilon 1}\left(j\right)& \frac{C_3}{2}{L}_{\epsilon 3}\left(d\right)& -\frac{C_3}{2}{L}_{\epsilon 3}\left(d\right)-\frac{C_1}{2}{L}_{\epsilon 1}\left(j\right)\end{array}\right]$$

According to the output equation, which is linear, ${\Phi }_2\left(\xi \right)=Cx\left(t\right)$; hence,

$$\frac{\partial {\Phi }_2\left(\xi \right)}{\partial x}=C=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\end{array}\right]$$

Therefore, ${\mathcal{C}}_i=C$.

Solving the LMI in Theorem 1, the following observer matrices are obtained:

$$L=\left[\begin{array}{cc}0.4840& 0.9309\\ -0.9247& 0.4900\\ 0.0010& 0.1682\end{array}\right],P=\left[\begin{array}{ccc}1.1432& -0.0016& -0.1489\\ -0.0016& 1.1300& -0.1619\\ -0.1489& -0.1619& 1.8552\end{array}\right]$$

4.3. Simulation Validation

The simulation has been validated by considering the initial condition as $x_0={\left[\begin{array}{ccc}0.08& 0.06& 0.07\end{array}\right]}^T$ and ${\widehat{x}}_0={\left[\begin{array}{ccc}0.181& 0.1610& 0.171\end{array}\right]}^T$. The system inputs are shown in Figure 3. The tanks levels and their estimation are shown in Figure 4.

5. Conclusions

This paper introduces a design for the Takagi–Sugeno observer using the mean value theorem, bypassing the commonly used Lipschitz assumption and the ${\mathcal{L}}_2$ attenuation-based method. While our method adeptly tracks the system’s states, it uniquely applies the MVT to systems with nonlinear outputs, contrasting prior works such as [8,9,13,14] that targeted only linear output systems. However, the proposed approach does have limitations, particularly for systems with unknown inputs, directing our future research ambitions. We aim to explore observer designs accommodating unknown inputs and to investigate emerging control system methodologies, like the adaptive fuzzy control for pneumatic active suspensions, as seen in [18]. This paves the way for the Takagi–Sugeno observer’s broader applications in complex systems.