Power-Yeoh: A Yeoh-Type Hyperelastic Model with Invariant I₂ for Rubber-like Materials ^†

Abstract

Rubber-based materials play an important role in various engineering and healthcare applications. Numerous hyperelastic models have been proposed in the long line of literature to model these nonlinear elastic materials. Due to the need to balance simplicity with accuracy, purely invariant I₁-based models have been proposed, which possess certain limitations with respect to the accurate description of their mechanical behaviors. In this paper, we improve the Yeoh model, a classical and popular I₁-based hyperelastic model with high versatility. The Yeoh model is modified by adding a generalized power-law type term. The model’s capabilities are analyzed under homogeneous deformation modes, such as uniaxial tensile, biaxial tensile and pure shear loading conditions. Experimental data pertaining to rubber-based materials are applied to the proposed hyperelastic model. Also, the interesting phenomenon of thin balloon expansion is investigated by applying the model to relevant experimental data on elastomeric balloons available in the literature. A genetic algorithm-based least squares optimization routine is carried out to determine the material constants while applying the reported experimental data. The results of curve fitting to experimental data pertaining to rubber-based materials showed the capability of the model to describe such multiaxial loading responses with acceptable accuracy (R² ≥ 0.95). The model also showed the capability to describe both the limit-point instability and the strain stiffening in thin rubber balloons, demonstrating its versatility and suitability for modeling rubber-like materials under various applications. The model’s performance can be further extended in the future by coupling terms related to anisotropy, compressibility, damage, etc., according to requirements.

1. Introduction

Hyperelastic materials can be stretched to many times their original length without breaking and exhibit large elastic deformation when subjected to external loads. These materials show a nonlinear relationship between stress and strain, enabling them to withstand high levels of deformation while returning to their original shape when the stress is removed. Hence, these materials are widely known for their exceptional resilience, shock absorption, damping, sealing capability, insulation, energy return, etc., making them an attractive option for various applications [1].

From the basis of continuum mechanics (assuming the bodies to be a continuum), hyperelastic materials have been represented by using mathematical formulations called strain–energy density functions (SEDFs), which represent the stored energy in the material upon the application of external loads. These formulations are a function of deformation of the body or strain. In continuum solid mechanics, the strain experienced by the body is expressed in terms of the invariants of the strain measures to ensure the frame indifference of the material models [2,3].

To describe the mechanical behavior of isostropic nonlinear elastic solids, three primary strain invariants, I₁, I₂ and I_3, are necessary. However, incompressibility is a common and realistic assumption in many scenarios, which reduces the necessary invariants to two (I₁ and I₂). Furthermore, in pursuit of ever simpler models with the minimum number of material constants [4], and yet capable constitutive formulations, numerous popular and classical hyperelastic models have been proposed in the literature containing only the first invariant (I₁), such as, neo-Hookean [5], Yeoh [6], Gent [7], Knowles [8], Davis-De-Thomas [9], Lopez-Pamies [10], gen-Yeoh [11], Fung-Demiray [12,13], Exp-Ln model [14], and so on. Nevertheless, it is important to note that purely I₁-based models are inherently associated with limitations with regard to the representation of some significant mechanical behaviors of isotropic solids [15,16], as well as the fundamental requirement of an accurate description of experimental data under multiaxial deformation states [17,18].

To overcome the limitations of these purely I₁-based models, several researchers have attempted to include various mathematical functions of invariant I₂ [18,19]. In this line of development, the present paper proposes a modified Yeoh model including a power-law-type function of invariant I₂. The descriptive capability of the model is demonstrated by applying it to a set of classical as well as recently reported experimental data on rubber-based materials.

2. Methodology

2.1. Proposed SEDF and Its Stress–Strain Relationships under Typical Homogeneous Deformation Modes

The basic Yeoh hyperelastic model is given by the following equation [6]

$$W={\sum }_{i=1}^3{C}_{i0}{\left(I_1-1\right)}^i,$$

(1)

where $C_{i0}$ ($i=1, 2, 3$) are the three material constants and $I_1$ is the first invariant of the right Cauchy–Green deformation tensor [2]. Following in the footsteps of other researchers in pursuit of improvements in the Yeoh model [11,20] and, in particular, generalizing the model proposed by Melly et al. (2022) [21], we propose a simple extended Yeoh model by including a power-law term of invariant I₂.

The Yeoh model was modified by including a term of invariant I_2, such that it forms a power-law function with a constant ‘$\alpha$’ in the exponent. This introduces an enhanced capability in the model to represent nonlinear mechanical characteristics due to the capability of the power law function to describe nonlinear relationships. Thus, the proposed form of W is

$$W={\sum }_{i=1}^3{C}_i{\left(I_1-3\right)}^i+B\left({I_2}^{\alpha }-3^{\alpha }\right),$$

(2)

where $C_i$ ($i=1, 2, 3$), $B$ and $\alpha$ are the five material constants, and $I_2$ is the second invariant of the right Cauchy–Green deformation tensor [2]. We call this, “Power-Yeoh”, the power law-appended Yeoh model SEDF. The strain invariants are expressed in terms of the principal stretches as [2,4]

$$I_1={\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2, I_2={\lambda }_1^2{\lambda }_2^2+{\lambda }_2^2{\lambda }_3^2+{\lambda }_2^2{\lambda }_1^2$$

(3)

Under uniaxial, equibiaxial and pure shear loading conditions, using the incompressibility constraint [2,4], the corresponding Cauchy stress–stretch relationships, respectively, can be derived, as shown in Equations (3)–(5) [2,4].

$${\sigma }_1=2\left({\lambda }^2-\frac{1}{\lambda }\right)\left[C_1+2C_2\left(I_1-3\right)+3C_3{\left(I_1-3\right)}^2-B\alpha \left({\lambda }^2-\frac{1}{\lambda }\right){I_2}^{\alpha }\right],$$

(4)

$${\sigma }_1={\sigma }_2=2\left({\lambda }^2-\frac{1}{{\lambda }^4}\right)\left[C_1+2C_2\left(I_1-3\right)+3C_3{\left(I_1-3\right)}^2-B\alpha \left({\lambda }^2-\frac{1}{{\lambda }^4}\right){I_2}^{\alpha -1}\right],$$

(5)

$${\sigma }_{12}=2\left({\lambda }^2-\frac{1}{{\lambda }^2}\right)\left[C_1+2C_2\left(I_1-3\right)+3C_3{\left(I_1-3\right)}^2+B\alpha {I_2}^{\alpha -1}\right].$$

(6)

Considering the case of inflation of a thin spherical balloon, the pressure–stretch relationship can be derived using the following equation [22]

$$p=\frac{2}{\lambda }\left[\frac{\partial W}{\partial I_1}\left(1-{\lambda }^{-6}\right)+\frac{\partial W}{\partial I_2}\left(1-{\lambda }^2-{\lambda }^{-6}+{\lambda }^{-10}\right)\right]$$

(7)

2.2. Genetic Algorithm Approach for Determination of Material Constants

Generally, Levenberg–Marquardt algorithm-based least squares optimization is carried out for the determination of hyperelastic material constants [23,24]. However, in this study, the genetic algorithm (GA), a stochastic optimization algorithm, is used for this purpose. The genetic algorithm works on the principle of genetic transmission of useful features by means of genetic inheritance to achieve the objective function to be satisfied. Here, an initial population is assumed, which encompasses the candidates of solutions. They are raised in a parallel fashion by means of mutation and crossover, determining the material constants satisfying the objective function [25]. Here, GA is employed by supplying the objective function to be minimized to the function ‘ga’ in MATLAB^® (MathWorks, Natick, MA, USA). The constants are kept positive to ensure polyconvexity of the SEDF [4]. For the uniaxial, equibiaxial and shear test data, Equations (4)–(6) were used in the objective function, whereas Equation (7) was applied to obtain the equation for the balloon expansion data.

2.3. Application to Experimental Data from Mechanical Loading Tests

Overall, two types of test data are utilized for demonstrating the capability of the Power-Yeoh model: firstly, classical test data on 8% Sulphur-vulcanized rubber [26] and relatively recent data on a thermoplastic elastomer [27] under uniaxial tensile, equibiaxial tensile and pure shear loading conditions; secondly, a classical pressure-inflation experimental result for an elastomeric thin-walled balloon [28], read from figures published in [29]. The data were extracted from published figures in the literature using the opensource tool WebPlotDigitizer 4.6 [30].

It is of vital importance to note that many of the conventional hyperelastic models do not provide a satisfactory description of multi-axial deformation models, of which, typically, uniaxial tensile, equibiaxial tensile and pure shear are used for benchmarking purposes [21]. Thus, in this paper, we consider the simultaneous description of all these deformation models, along with the interesting case of the inflation of balloon expansion.

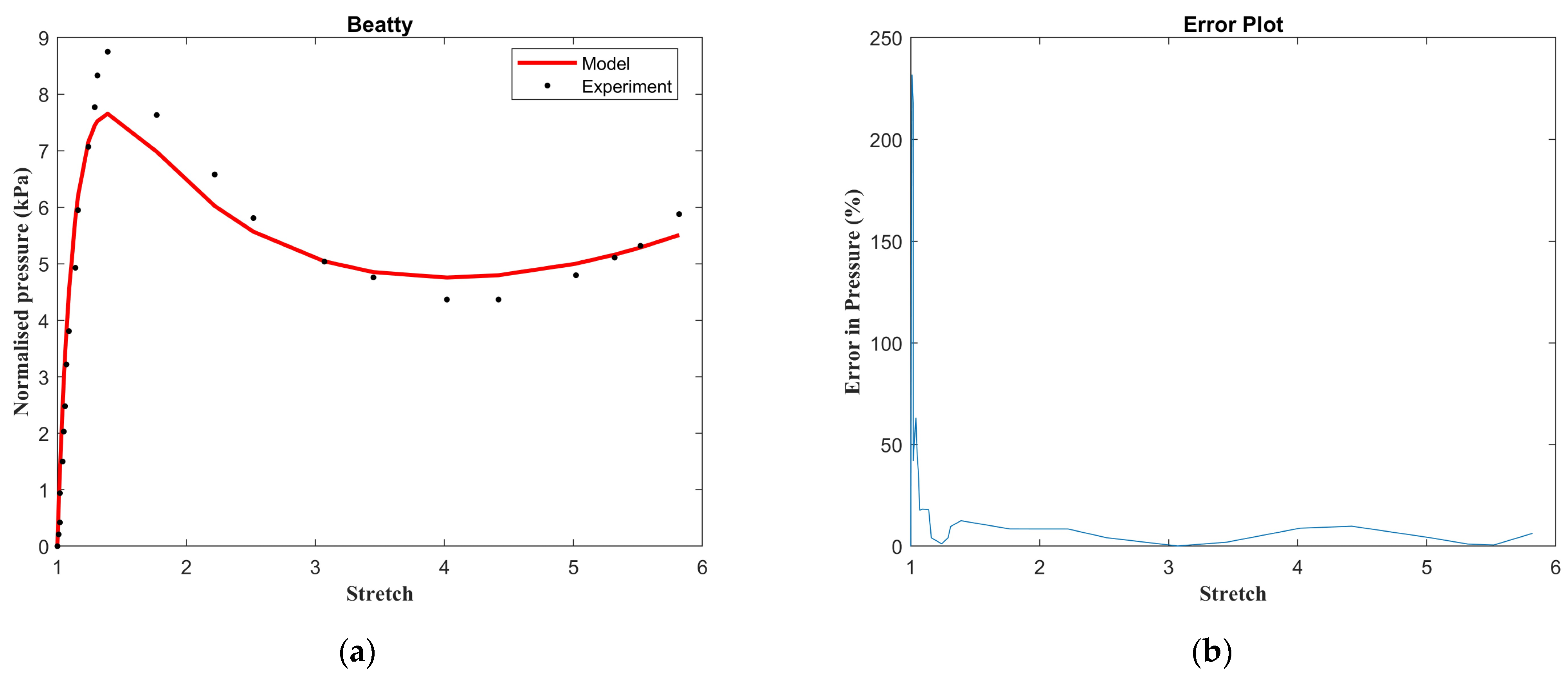
3. Results

3.1. Descriptive Capability of Uniaxial Tensile, Biaxial Tensile and Pure Shear Test Data

Figure 1 shows the curve-fitting results of the Power-Yeoh model with respect to the experimental data of Treloar (1944) [26] and Zhao (2016) [27]. Figure 1a,c show that the model is able to depict the multi-axial deformation models of the rubber-based materials with a reasonable accuracy.

Figure 1b,d show the relative error plots, which is computed according to [4,23], where it is observed that, except the low-strain regimes of strains < 2, the errors are <10%. Overall, the Power-Yeoh model shows reasonable capability of depicting the large-deformation behaviors of rubber-based materials. The material constants and the coefficient of determination (R²) obtained during the curve fitting shown in Figure 1 are listed in

Table 1. Material constants obtained for Treloar [26], Zhao [27] and Beatty [28] data.

Author (Year)	C1 (MPa)	C2 (MPa)	C3 (MPa)	B (MPa)	α	R2
Treloar (1944) [26]	0.14522	0.00123	0.00002	26.76127	0.00242	0.9559
Zhao (2016) [27]	0.10748	0	0.00002	0.20239	0.04508	0.9730
Beatty (1987) [28]	6.09489	0.0395	0.0004	26.78974	23.06651	0.9456

. It is observed that the R² for the combined curve fitting is >0.95 for both cases, demonstrating the accuracy of curve fit.

3.2. Descriptive Capability of Balloon Inflation Test Data

Figure 2 shows the curve-fitting results of the Power-Yeoh model to rubber inflation test data shown in Beatty (1987) [28]. It is observed (Figure 2a) that the Power-Yeoh model is able to depict both the limiting pressure and the strain stiffening observed in the thin balloon expansion, which is the typically observed nature of inflation behavior of thin balloons [29]. The error plot shows that the errors are in the range of <10% for the largest portion of the stretching regime, indicating good fitting. The R² for this curve fitting (see Table 1) is approximately 0.95, which indicates good descriptive accuracy.

4. Discussion

This study presented the results obtained using the newly proposed Power-Yeoh model to describe the behaviors of rubber materials using relevant experimental data from the literature. The results of curve fitting revealed the performance of this model in simultaneously describing the mechanical behavior under multiaxial loading conditions. As noted by other researchers, it is of critical importance for a constitutive model to be able to reasonably describe all the typical deformation modes that the bodies can undergo [15,18,20,21]. With regard to the descriptive accuracy, Melly et al. (2022) [21] found that the Yeoh model (Equation (1)) shows an overall R² value of 0.87 to both Treloar’s and Zhao’s data. In this study, we showed that it has increased to 0.9559 and 0.9730, respectively, which is an increase of around 10% compared to the original model.

Another aspect is the interesting observation of the pressure–inflation relationship of thin rubber balloons. It is a common observation that balloons expand rapidly after a certain point of expansion and later again stiffen up before bursting. Notably, it is a common understanding in the literature that purely I₁-based models are incapable of modeling both the limit-point instability at low stretches and the strain-stiffening phenomenon at higher stretches, which are the common observations in thin rubber balloons [28,29,31]. However, the proposed model is able to overcome this limitation, as shown in Figure 2.

Since the analytical performance of the model has been established, it can now be implemented in commercial finite element codes by writing the user-material subroutines, as described in [11,17,18]. This opens the doors to extend the potential of the model with more complex phenomena, such as anisotropy, damage, viscous effects, etc. Thereby, the model can be used in simulating various real-life engineering and healthcare problems, such as performance of rubber components in tires, rubber tracks, vehicle seals and vibration-isolation devices, response of papillary muscles of the heart, mechanics of blood vessel tissues, etc. [16,18,32,33,34], wherein simple I₁-based models would fail to capture the nonlinear nature of the mechanical responses exhibited by rubber-based materials [18]. For instance, I₁-based models fail to capture the shear and torsional deformations, as well as the celebrated Poynting effect observed in isotropic nonlinear-elastic materials [16].

5. Conclusions

This paper presented an improvised version of the classical Yeoh model by adding a power-law term of invariant I₂. Its capability to simultaneously describe multi-axial deformation modes of rubber-like materials was evaluated by applying it to reported experimental data from the literature. Further, the interesting phenomenon of strain stiffening of thin rubber balloons was represented accurately by the model. Thus, a detailed analytical investigation of the model is presented. The model demonstrated its adaptability and capability to reflect the nonlinear mechanical behaviors of rubber-based materials under multiaxial deformation models by describing the experimental data (uniaxial, equibiaxial and pure shear models, and also inflation of thin balloons) with excellent accuracy (R² ≥ 0.95). The model can now be employed in finite element simulations by writing user-material subroutines in commercial software. Furthermore, it is suggested to extend the versatility of the model by including additional physical phenomena, such as anisotropy, damage, etc., to suit the requirements of more challenging problems.