Role of Computational Material Science in Improving the Properties of Piezoelectric Smart Materials: A Review †
Abstract
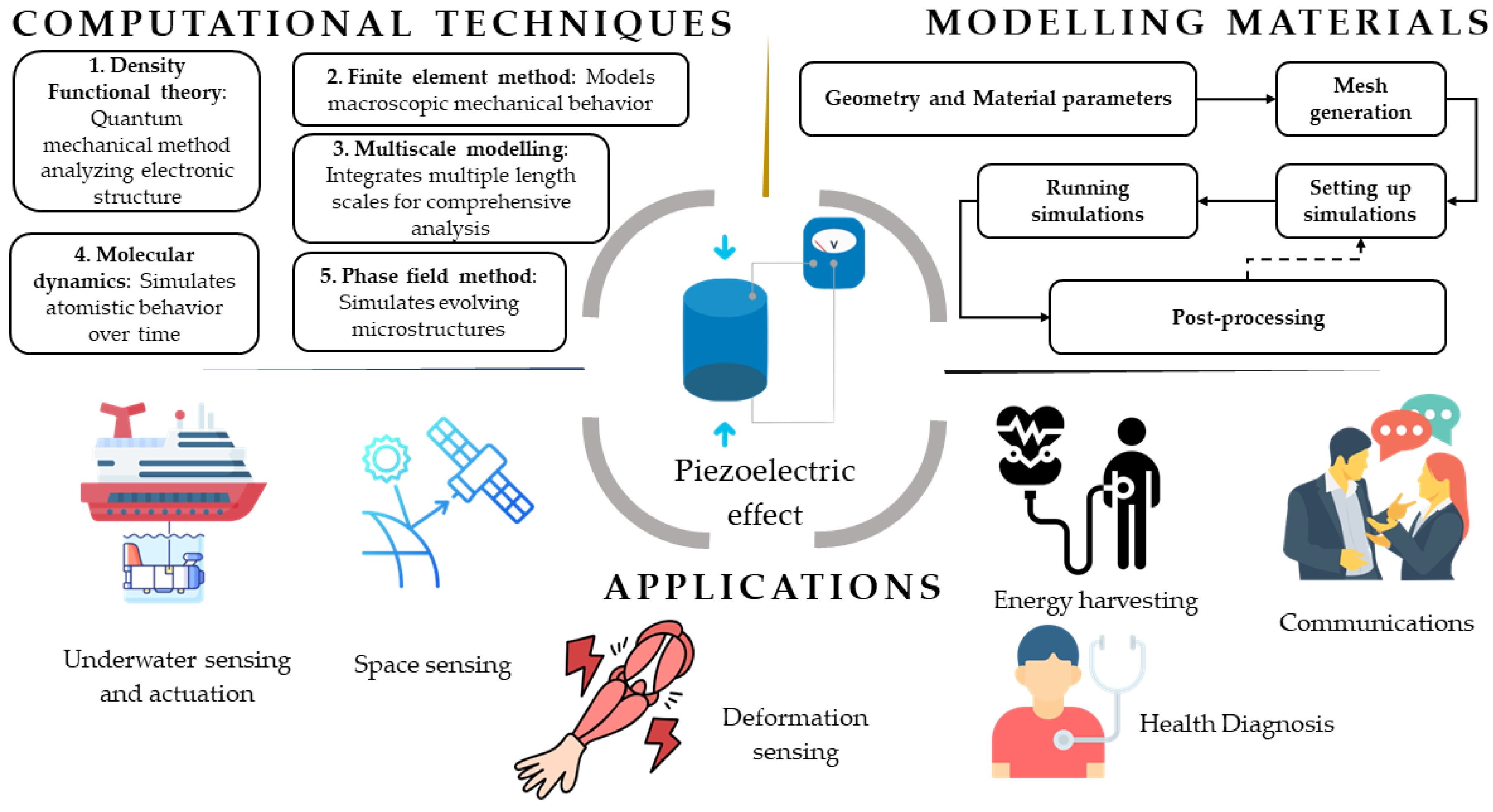
:1. Introduction
2. Literature Review
2.1. Computational Modeling Techniques
2.1.1. Density Functional Theory (DFT)
2.1.2. Finite Element Analysis (FEA)
2.1.3. Molecular Dynamics (MD) Simulations
2.1.4. Phase Field Method (PFM)
2.1.5. Multiscale Modelling Approaches
3. Summary
Challenges and Future Directions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kanchan, M.; Santhya, M.; Bhat, R.; Naik, N. Application of Modeling and Control Approaches of Piezoelectric Actuators: A Review. Technologies 2023, 11, 155. [Google Scholar] [CrossRef]
- Rogers, C.A. U.S. Army Research Office Workshop on Smart Materials, Structures and Mathematical Issues. In Proceedings of the U.S. Army Research Office Workshop, Blacksburg, VA, USA, 15–16 September 1988. [Google Scholar]
- Raabe, D. Computational Materials Science; Wiley: Hoboken, NJ, USA, 1998. [Google Scholar]
- Mason, W.P. Piezoelectricity, its history and applications. J. Acoust. Soc. Am. 1981, 70, 1561–1566. [Google Scholar] [CrossRef]
- Mindlin, R.D. Elasticity, piezoelectricity and crystal lattice dynamics. J. Elast. 1972, 2, 217–282. [Google Scholar] [CrossRef]
- Mould, R.F. Pierre Curie, 1859–1906. Curr. Oncol. 2007, 14, 74–82. [Google Scholar] [CrossRef]
- Curie, J.; Curie, P. Development par compression de l’électricité polaire dans les cristaux hémièdres à faces inclines. Bull. Minéralogie 1880, 3, 90–93. [Google Scholar]
- Curie, J.; Curie, P. Contractions et dilatations produites par des tensions électriques dans les cristaux hémièdres à faces inclines. Compt. Rend 1881, 93, 1137–1140. [Google Scholar]
- Jiao, P.; Egbe, K.-J.I.; Xie, Y.; Nazar, A.M.; Alavi, A.H. Piezoelectric Sensing Techniques in Structural Health Monitoring: A State-of-the-Art Review. Sensors 2020, 20, 3730. [Google Scholar] [CrossRef]
- Gautschi, G. Piezoelectric Sensors. In Piezoelectric Sensorics; Springer: Berlin/Heidelberg, Germany, 2002; pp. 73–91. [Google Scholar]
- Liu, J.-M.; Pan, B.; Chan, H.L.W.; Zhu, S.N.; Zhu, Y.Y.; Liu, Z.G. Piezoelectric coefficient measurement of piezoelectric thin films: An overview. Mater. Chem. Phys. 2002, 75, 12–18. [Google Scholar] [CrossRef]
- Yourdshahyan, Y.; Grinberg, I.; Sai, N.; Cooper, V.R.; Mason, S.E.; Rappe, A.M.; Kauffman, R.P. Relating fundamental chemistry and smart materials with DFT calculations. In Proceedings of the User Group Conference, Bellevue, WA, USA, 9–13 June 2003; IEEE: Piscataway, NJ, USA; pp. 20–25. [Google Scholar]
- Yuan, S.; Io, W.F.; Mao, J.; Chen, Y.; Luo, X.; Hao, J. Enhanced Piezoelectric Response of Layered In2Se3/MoS2 Nanosheet-Based van der Waals Heterostructures. ACS Appl. Nano Mater. 2020, 3, 11979–11986. [Google Scholar] [CrossRef]
- Chen, Y.; Tang, Z.; Shan, H.; Jiang, B.; Ding, Y.; Luo, X.; Zheng, Y. Enhanced out-of-plane piezoelectric effect in transition metal dichalcogenide heterostructures. Phys. Rev. B 2021, 104, 075449. [Google Scholar] [CrossRef]
- Hermet, P. Trigonal BiPO4: A potential piezoelectric for low-temperatures. Comput. Mater. Sci. 2016, 118, 1–3. [Google Scholar] [CrossRef]
- Nguyen, V.-T.; Kumar, P.; Leong, J. Finite Element Modelling and Simulations of Piezoelectric Actuators Responses with Uncer tainty Quantification. Computation 2018, 6, 60. [Google Scholar] [CrossRef]
- Nguyen-Vinh, H. Extended finite element method for dynamic fracture of piezo-electric materials. Eng. Fract. Mech. 2012, 92, 19–31. [Google Scholar] [CrossRef]
- Gu, S.-T.; Liu, J.-T.; He, Q.-C. Piezoelectric composites: Imperfect interface models, weak formulations and benchmark problems. Comput. Mater. Sci. 2014, 94, 182–190. [Google Scholar] [CrossRef]
- Hong, H.; Song, S.A.; Kim, S.S. Phase transformation of poly (vinylidene fluoride)/TiO2 nanocomposite film prepared by microwave-assisted solvent evaporation: An experimental and molecular dynamics study. Compos. Sci. Technol. 2020, 199, 108375. [Google Scholar] [CrossRef]
- Tang, T. Stretchable polymer composites with ultrahigh piezoelectric performance. Natl. Sci. Rev. 2023, 10, nwad177. [Google Scholar] [CrossRef]
- Chakrabarty, A.; Çağın, T. Thermo-mechanical properties of a piezoelectric polyimide carbon nanotube composite: Assessment of composite theories. Comput. Mater. Sci. 2014, 92, 185–191. [Google Scholar] [CrossRef]
- Yan, Y.; Zhou, J.E.; Maurya, D.; Wang, Y.U.; Priya, S. Giant piezoelectric voltage coefficient in grain-oriented modified PbTiO3 material. Nat. Commun. 2016, 7, 13089. [Google Scholar] [CrossRef]
- Yan, Y. Near-ideal electromechanical coupling in textured piezoelectric ceramics. Nat. Commun. 2022, 13, 3565. [Google Scholar] [CrossRef]
- Leng, H. Water Quenched and Acceptor-Doped Textured Piezoelectric Ceramics for Off-Resonance and On-Resonance Devices. Small 2023, 19, 2204454. [Google Scholar] [CrossRef]
- Maruccio, C.; De Lorenzis, L.; Persano, L.; Pisignano, D.; Zavarise, G. Multiscale Modeling of Piezoelectric Materials; Army Research Laboratory: Adelphi, MD, USA, 2013. [Google Scholar]
- Wang, L.; Lin, Z.; Du, Y.; Qiu, J.; Chen, X.; Yu, J. The piezoelectricity of 2D Janus ZnBrI: Multiscale prediction. Chem. Phys. Lett. 2022, 794, 139506. [Google Scholar] [CrossRef]
- Lv, J.; Zhang, H.; Gao, X.; Huang, Y. A new multiscale computational method for electromechanically coupled analysis of heterogeneous piezoelectric composites. J. Intell. Mater. Syst. Struct. 2015, 26, 434–449. [Google Scholar] [CrossRef]
- Hong, Y.; Hou, B.; Jiang, H.; Zhang, J. Machine learning and artificial neural network accelerated computational discoveries in materials science. WIREs Comput. Mol. Sci. 2020, 10, e1450. [Google Scholar] [CrossRef]
- Zheng, B.; Chang, C.-J.; Gea, H.C. Topology optimization of energy harvesting devices using piezoelectric materials. Struct. Multidiscip. Optim. 2009, 38, 17–23. [Google Scholar] [CrossRef]
| Technique | Advantages | Limitations | Applications |
|---|---|---|---|
| Density Functional Theory | Accurate electronic properties can handle complex materials. | Computationally intensive; limited to small systems. | Design of novel piezoelectric materials; investigation of electronic properties. |
| Molecular Dynamics | Captures dynamic behavior applicable to large systems. | Limited to short time scales; relies on force field accuracy. | Study of piezoelectric polarization switching; investigation of defect effects. |
| Finite Element Analysis | Handles complex geometries can model various boundary conditions. | Requires mesh generation may lack atomic-level accuracy. | Design of piezoelectric sensors, actuators, and transducers. |
| Phase Field Method | Captures complex microstructural changes; suitable for multiphase systems. | Captures complex microstructural changes; suitable for multiphase systems. | Study of domain switching; ferroelectric domain structures in piezoelectric materials. |
| Multiscale Modelling | Captures interactions from atomistic to macroscopic scales. | Complex setup and calibration; computational costs can be high. | Investigating piezoelectric material behavior across different length scales; linking molecular and macroscopic behavior. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
V., A.K.; Kamath, R.C. Role of Computational Material Science in Improving the Properties of Piezoelectric Smart Materials: A Review. Eng. Proc. 2023, 59, 21. https://doi.org/10.3390/engproc2023059021
V. AK, Kamath RC. Role of Computational Material Science in Improving the Properties of Piezoelectric Smart Materials: A Review. Engineering Proceedings. 2023; 59(1):21. https://doi.org/10.3390/engproc2023059021
Chicago/Turabian StyleV., Amith K., and Raghavendra C. Kamath. 2023. "Role of Computational Material Science in Improving the Properties of Piezoelectric Smart Materials: A Review" Engineering Proceedings 59, no. 1: 21. https://doi.org/10.3390/engproc2023059021
APA StyleV., A. K., & Kamath, R. C. (2023). Role of Computational Material Science in Improving the Properties of Piezoelectric Smart Materials: A Review. Engineering Proceedings, 59(1), 21. https://doi.org/10.3390/engproc2023059021






