The Characterization of Deformable Photovoltaic Modules ^†

Abstract

The system under investigation is a deformable photovoltaic–wind hybrid system which utilizes both solar and wind energy by combining PV modules with a vertical-axis wind turbine. This system contains 5 PV modules separated by 72° angles; these modules are attached to the blades of the vertical-axis wind turbine. This leads to each module receiving a different amount of solar irradiation, which affects the generated output power. In this study, the V_OC and I_SC of the modules were measured against different factors that influence the output power, including factors such as solar insulation, module temperature, module tilt angle θ, and module azimuth angle ϕ. These measurements were entered into the MATLAB curve fitter to produce a model of each parameter. The results showed that as the tilt angle θ decreased from the default, the V_OC increased slightly, while I_SC increased significantly. And when the module temperature increased, V_OC decreased significantly, while the I_SC increased slightly. The results of the study showed that by changing the module tilt angle and module azimuth angle, the solar insolation received at the module surface changed, which leads to different V_OC and I_SC values. Also, this study showed that the V_OC and I_SC values varied with time.

1. Introduction

Among the various alternative energy sources, solar energy holds a significant position [1]. Solar energy studies still lack information regarding solar radiation and its components at a specific location [2]. Many countries have embraced solar energy due to its beneficial features, which include the fact that it is infinite, eco-friendly, quiet, and requires low-maintenance expenses [3]. Since 2010, more measures have been taken to improve the world’s photovoltaic (PV) capacity than in the previous 40 years [4]. Recently, there has been an enormous increase in the understanding of the operational principle of photovoltaic devices, which has led to a rapid increase in power [5]. Regarding PV modules, higher temperatures can have a negative impact on their efficiency, leading to a reduction in the amount of power generated [6]. Raising the operating temperature of a PV system causes a decline in its open-circuit voltage, fill factor, and power output. This, in turn, results in a decrease in the conversion efficiency and can potentially harm the material of the PV module [7]. The parameters of PV modules are not constant, and they can be affected by the level of irradiation and temperature. The short-circuit current is not linearly proportional to the irradiation, and the same is true for the photocurrent, while the shunt resistance is more sensitive to changes in irradiation compared to the series resistance [8]. Investigating the impact of environmental factors on photovoltaic performance revealed that a high air temperature led to a decrease of 1.85–20.22% in the generated power, while high humidity caused the biggest reduction of 32.23% [9]. The impact of wind speed on the PV module’s surface temperature resulted in the temperature decreasing as the wind speed increased [10]. A study on global radiation in Jeddah, Saudi Arabia, concluded that to receive the maximum amount of energy from the PV module, the module should be tilted by an angle of 15° ± altitude (+ for winter; − for summer) [11]. Any module with optimal tilt angle installation will produce 7–8% extra power for any location [12]. Shading from nearby surroundings make using modules facing the equator to be difficult [13]. The output I-V and P-V characteristics were used to compare the MPP tracking and various parameters, including peak current, peak voltage, open-circuit voltage, and short-circuit current values, after examining various models. The manufacturer’s specifications were then compared to the findings of [14]. Here’s a step-by-step guide for simulating PV cells, modules, and arrays using Tag tools in MATLAB/Simulink. We will be using the DS-100M solar panel as a reference model, which has output characteristic curves that match the DS-100M panel [15].

2. Methodology

The purpose of this document is to create a model for a photovoltaic (PV) module using various parameters. To achieve this goal, an investigation was conducted to determine the impact of temperature, tilt angle, azimuth angle, solar irradiation, and time on the V_OC and I_SC of a PV module. This document includes two main experiments, one measuring an entire system with five PV modules, and the other involving the creation of a model for each parameter using a single PV module.

2.1. Measuring V_OC and I_SC for the Whole System

The system under investigation uses 5 PV modules attached to the blades of a vertical-axis wind turbine; the modules are connected in parallel. The study should include readings from different directions to cover the maximum number of possible positions of the modules. The specifications of the PV modules used in this experiment are listed in

Table 1. Specifications of the PV Modules used.

Specification	Description
Solar cell	Monocrystalline silicon cell
Dimensions	750 × 70 × 2 mm
ISC	0.33 A
VOC	24 V
Pm	8 W
Efficiency	19–20%

.

The system set-up is shown in Figure 1, where the 5 PV modules are attached to the blades of the turbine and tilted to a specific tilt angle, and each PV has a different direction; the tilt angle of the module was varied using a simple geared motor controlled by an Arduino microcontroller.

A temperature sensor was attached to the surface of the PV module to record the PV temperature, and the 5 DC geared motors were needed to push the PV modules to a specific tilt angle. The tilt angle used in this study varied between 75° and 55°, with a decrement of 5°. A multimeter was used to measure the V_OC and I_SC at each tilt angle. Furthermore, a Solmetric sensor was used to measure the solar irradiation at each tilt angle at different azimuth angles, starting from 0°, which represents the true south, going west with an increment of 45°. The Solmetric sensor was attached to a vertical slider, which was connected to a linear actuator, with a 12 V battery, all fitted on a wooden plate. The linear actuator was used to vary the tilt angle of the sensor, while the azimuth angle was varied using a DC motor located under the wooden plate to rotate the whole system to the required azimuth angle.

2.2. Modeling Using a Single PV Module

The study conducted on a single PV module involved modeling different parameters, such as temperature, irradiation, tilt angle, azimuth angle, and time. Each parameter was recorded independently from the others. The module temperature was modeled by observing the V_OC and I_SC at fixed tilt and azimuth angles while heating the PV module using a hot air blower. The tilt angle was modeled by fixing the other parameters while changing the module’s tilt angle after stabilization and recording the V_OC and I_SC at those angles. The azimuth angle was modeled by rotating the PV module at a fixed tilt angle, starting from 0° as a compass south and going west with an increment of 24° while measuring the V_OC and I_SC at each azimuth angle. Solar irradiation was modeled by recording the solar irradiation at different tilt angles and measuring the V_OC and I_SC at each point of solar irradiation. Lastly, time was modeled between 10:00 and 15:00, with an increment of 15 min, while the module was facing south at a fixed tilt angle, and new values of V_OC and I_SC were recorded for each increment.

3. Measurement

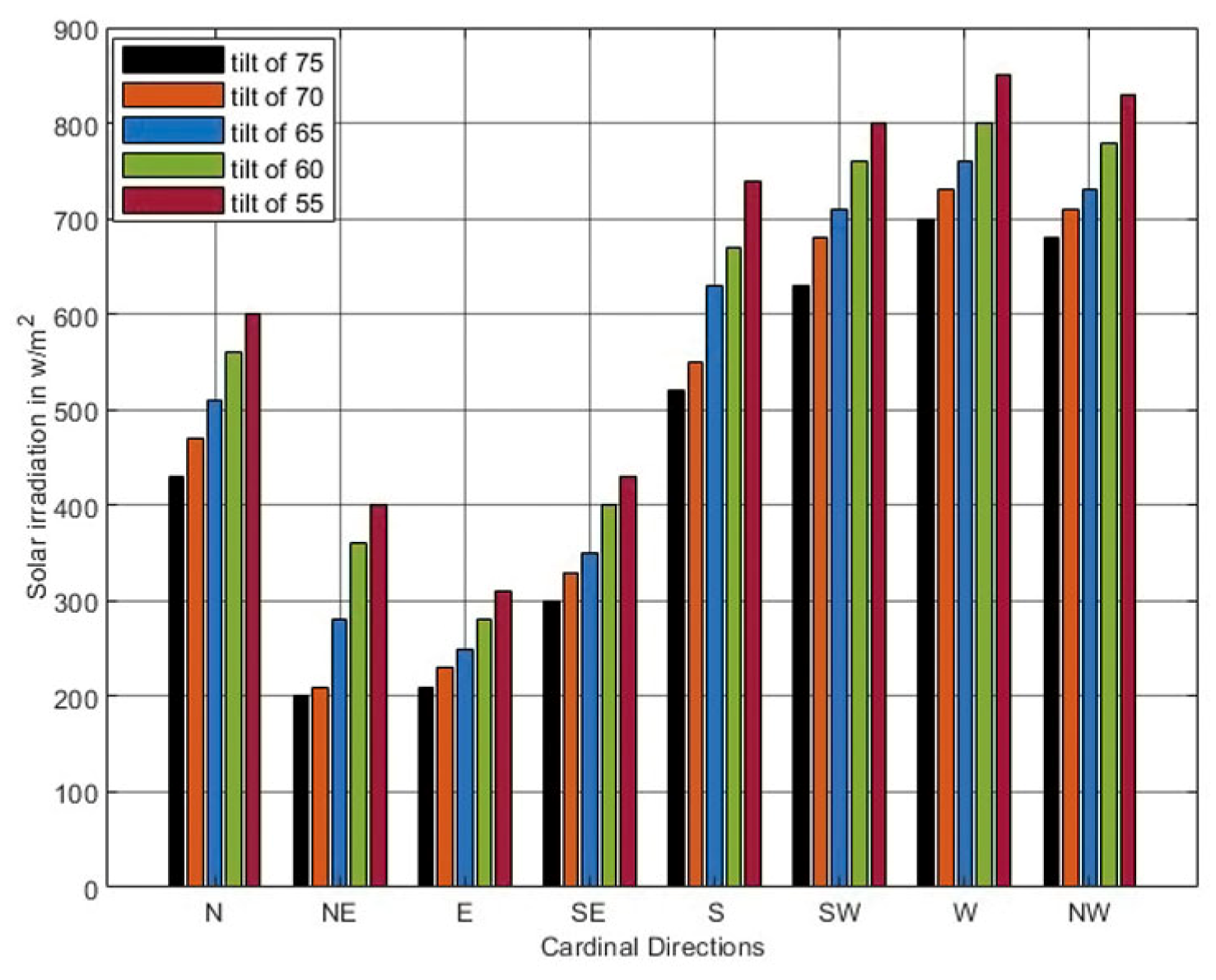
3.1. Solar Irradiation Measurement

The measurements were taken at Abu Dhabi University at different times (around noon time) using a Sol Sensor from Solmetric to obtain the irradiation in W/m². Referring to Figure 2 below, which represents sample data for a given day via a plot of solar irradiation against the cardinal direction, the solar insulation was higher when the module was mounted to the south going west and the tilt angle was 55°; with a tilted module, we can expect that the solar radiation will be normal or close to normal on the module surface.

3.2. Measuring the V_OC and I_SC of the Whole System

The PV modules used in this system were attached to the blades of a wind turbine and connected in parallel. Figure 3 represents the measured I_SC and V_OC values for each tilt angle at two different module temperatures. We can conclude that as the tilt angle decreased, the I_SC of the module increased, while the V_OC slightly increased; as a result, the power output increased. These results agree with the information in Figure 1, as when more solar irradiation is received, the higher the generated current is. Also, as the module temperature increased, the V_OC decreased, while the I_SC increased slightly.

4. Results and Discussion

Modeling such a system is challenging as there is more than one factor influencing the output power to consider; therefore, the idea is to take one module of the system and model the output from it with each factor independently, i.e., as each factor is taken, while the others are constants. The models suggested in this document model V_OC and I_SC with module temperature, solar irradiation, tilt angle, azimuth angle, and the time of day.

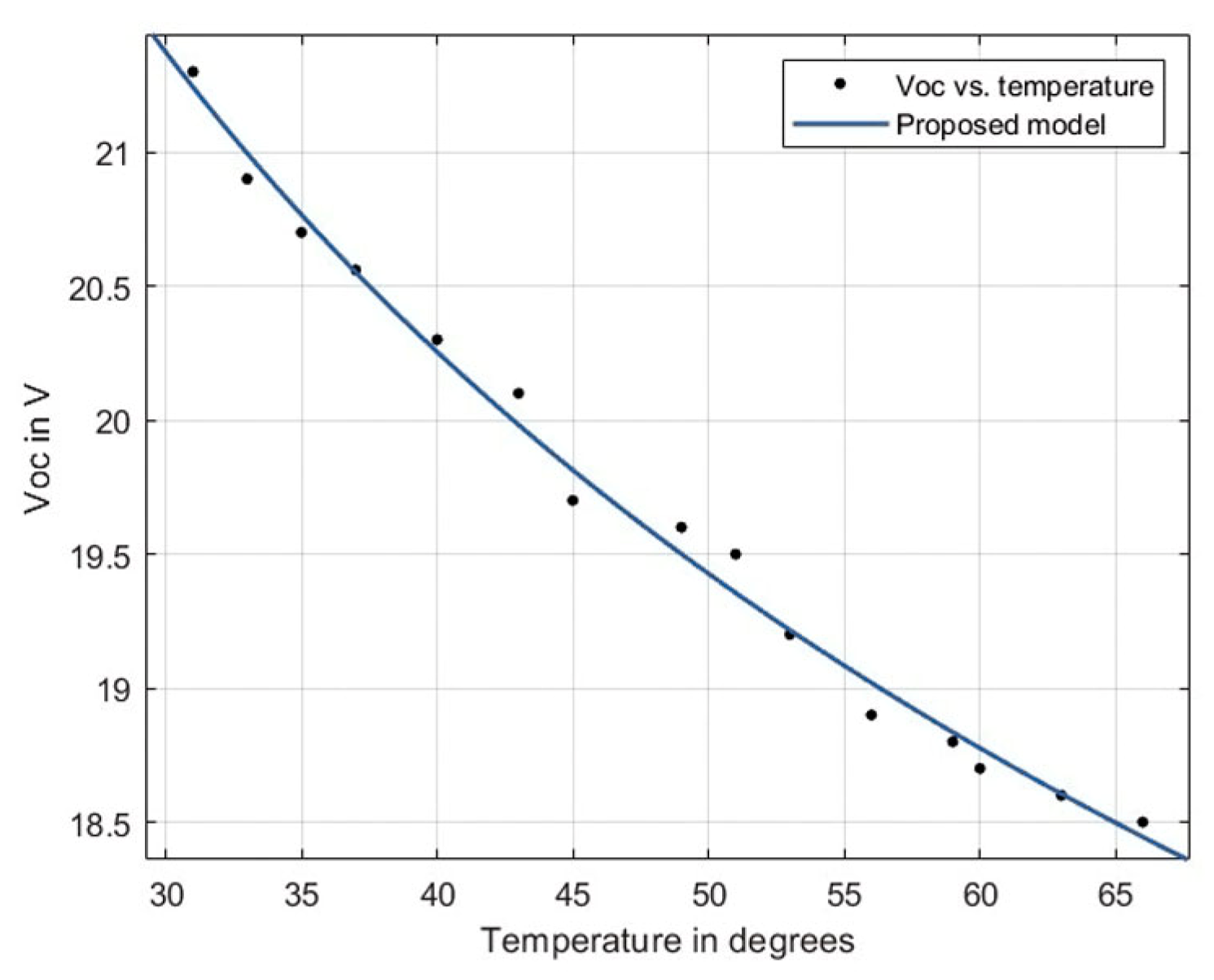
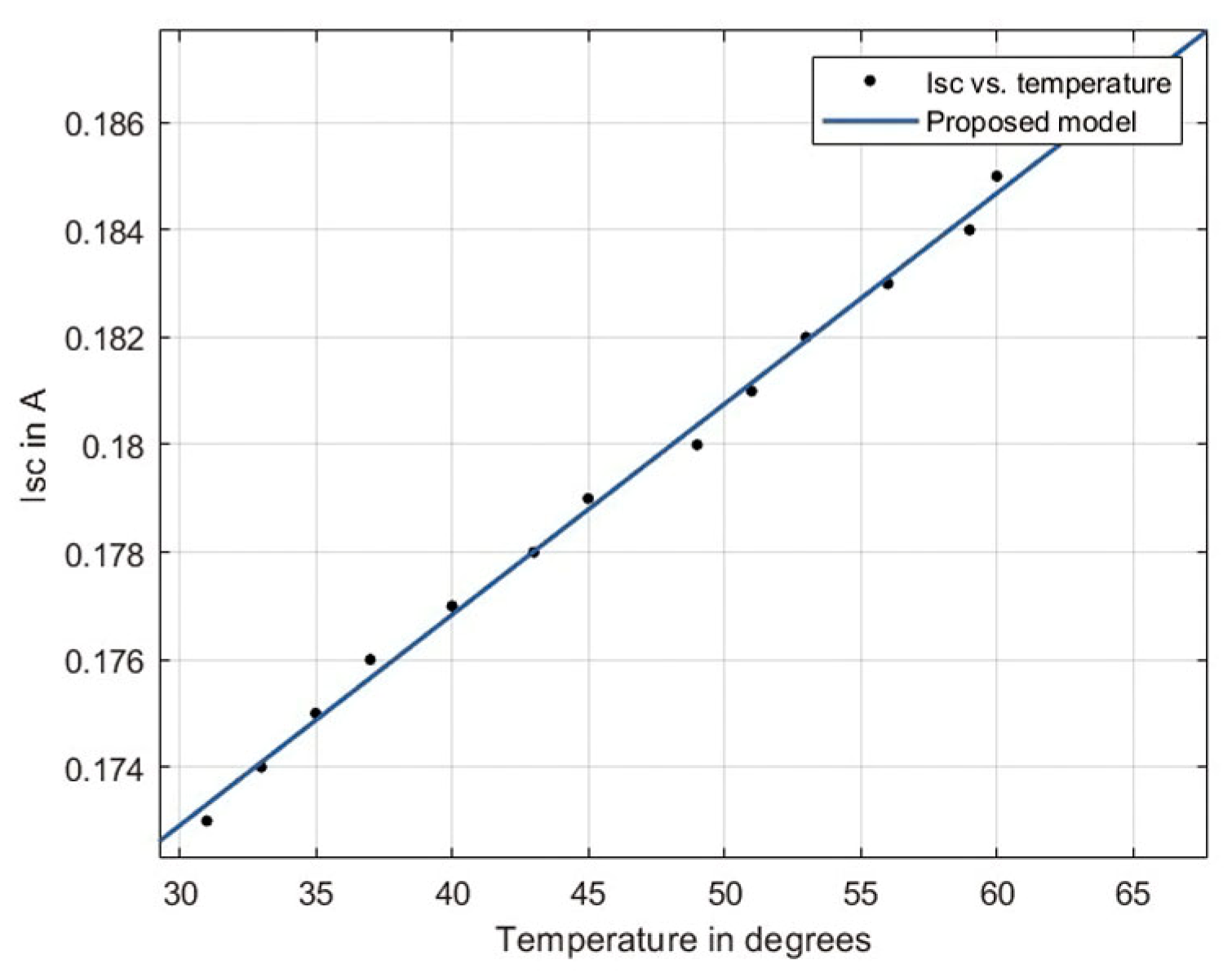
4.1. Modeling V_OC and I_SC with PV Temperature

The open-circuit voltage (V_OC) and short-circuit current ($\mathrm{I}\mathrm{s}\mathrm{c}$) of a photovoltaic (PV) module are influenced by the temperature of the PV module. A PV module’s V_OC decreases as the temperature increases. The temperature coefficient of V_OC, which is normally provided by the manufacturer of the PV module, can be used to describe this relationship. In this study, the temperature coefficient is not given; the V_OC and I_SC measured against the module temperature at fixed solar irradiation (750 W/m²) and a tilt angle of 60°, where the PV was facing south, is used to describe the relationship between them, as well as the increase in module temperature measured using a hot air blower, to raise the module temperature to high values. The measurements were taken on Monday 26th of June at 14:00. As shown in Figure 4, the model can be described using Equation (1).

$${\mathrm{V}}_{\mathrm{OC}}=22.11\times {\left(\frac{T}{T_o}\right)}^{-0.187},$$

(1)

where $T$ is module temperature in degrees, and $T_o$ is module temperature under STC conditions.

The short-circuit current (${\mathrm{I}}_{\mathrm{SC}}$) of a PV module generally increases with increasing temperature. Figure 5 shows the relationship between ${\mathrm{I}}_{\mathrm{SC}}$ and module temperature, and it can be described using Equation (2).

$${\mathrm{I}}_{\mathrm{SC}} = 0.0098\times \left(\frac{T}{T_o}\right)+0.161.$$

(2)

In Figure 4 and Figure 5, the data show a logarithmic decrease in the V_OC as the PV surface temperature increased; however, this was not the case for the current, as the results showed a linear increase in the current as the PV surface temperature increased. The level of the decrease in the V_OC is higher than the level of the increase in the I_SC, which results in a total power reduction.

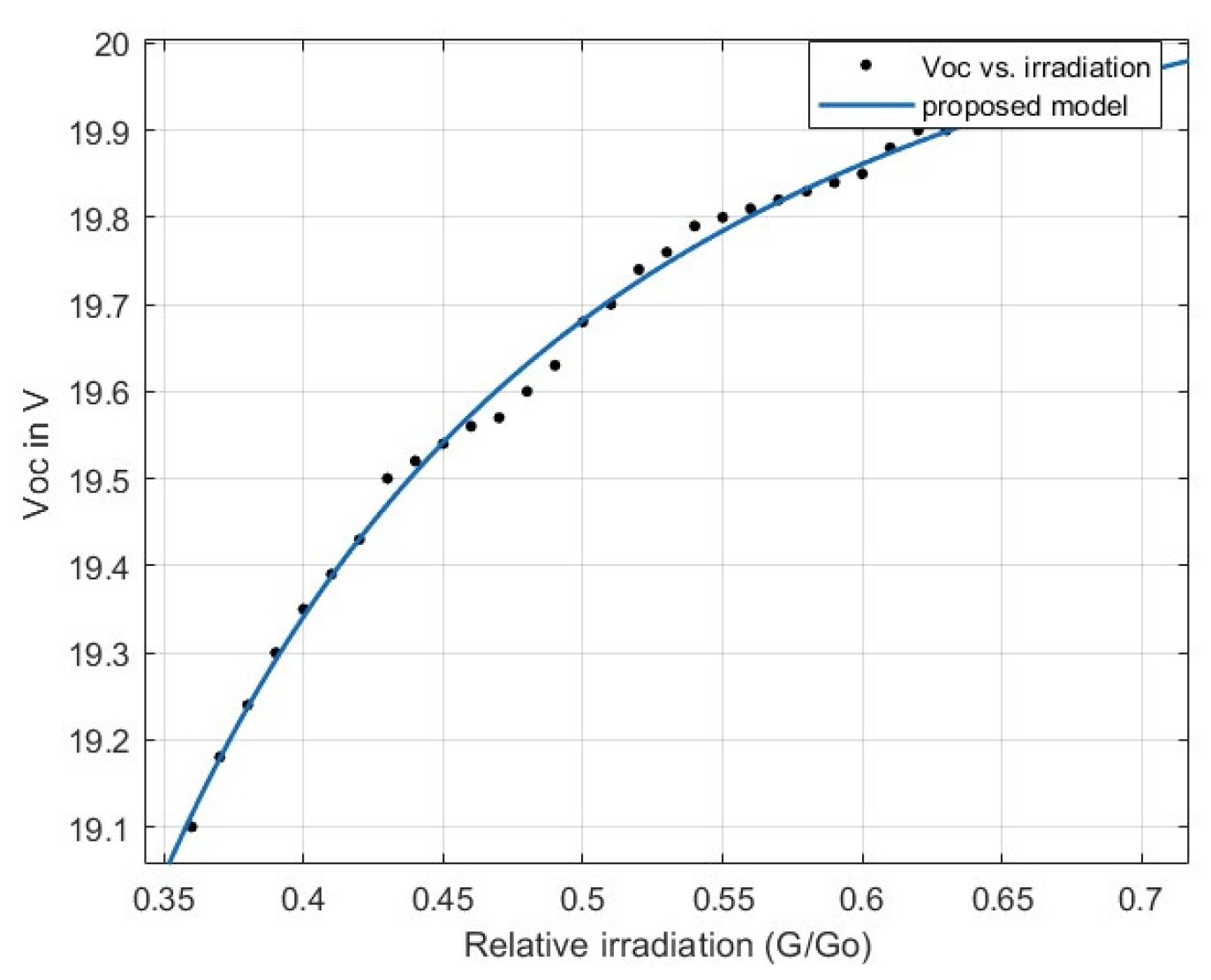
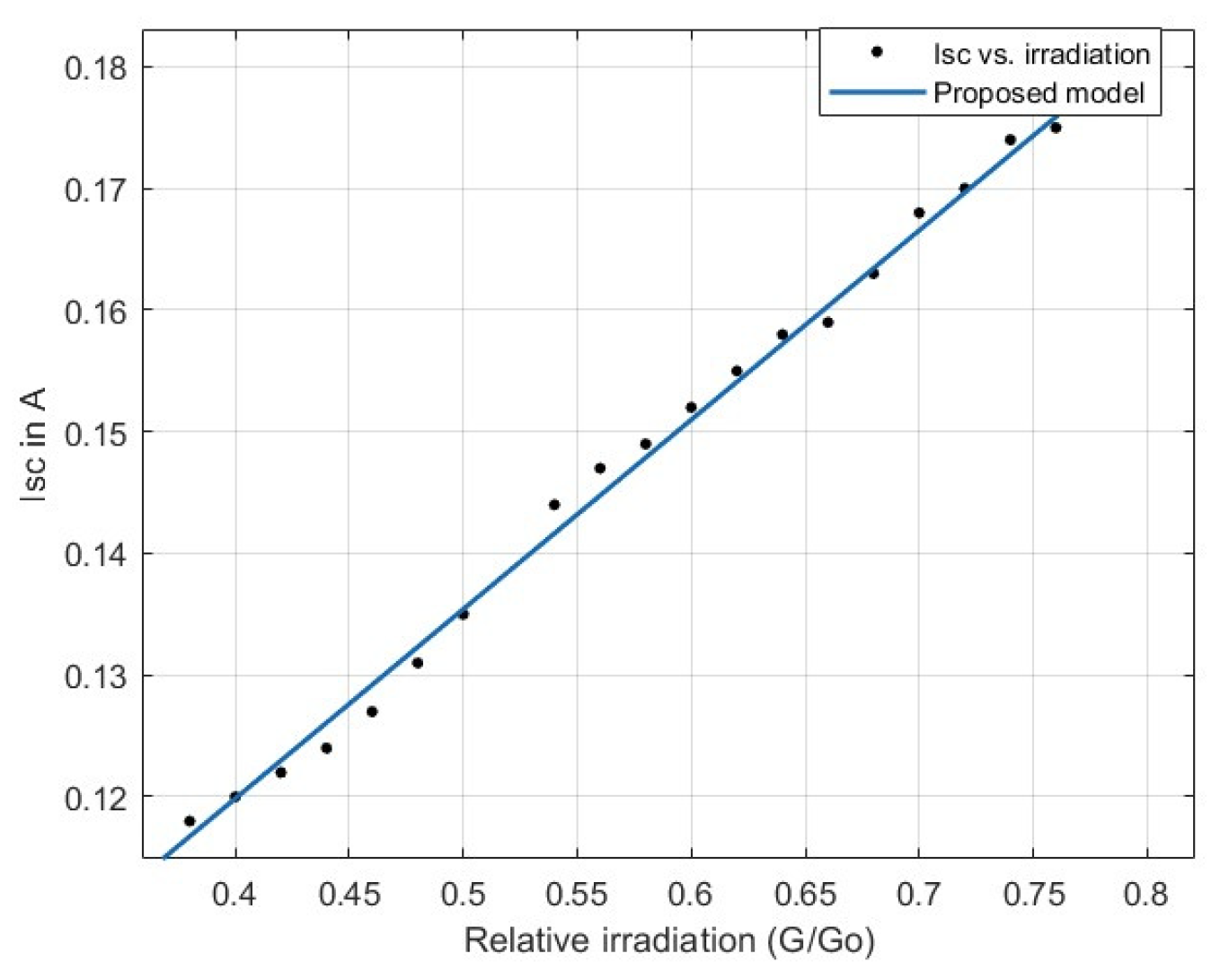
4.2. Modeling V_OC and I_SC with Solar Irradiation

V_OC can vary slightly with changing irradiance levels; this effect is relatively small compared to other factors such as temperature. In most practical situations, changes in solar irradiation have a minimal impact on V_OC. Figure 6 illustrates the effect of changing solar irradiation by varying the module tilt angle on the module’s V_OC. These measurements were taken on Tuesday 27 June 2023 at noon time; the module was facing south, and the change in tilt angle was used to vary the solar irradiation at an almost fixed temperature.

The model used to describe Figure 6 is shown in Equation (3).

$${\mathrm{V}}_{\mathrm{OC}}=-0.124\times {\left(\frac{G}{G_o}\right)}^{-2.16}+20.23,$$

(3)

where G_o is the solar irradiation under STC conditions of 1000 W/m².

The short-circuit current (I_SC) of a PV module is directly proportional to the solar irradiation. As the intensity of sunlight increases, I_SC also increases. This linear relationship holds true if the PV module operates within its normal operating range. The I_SC is primarily determined by the amount of light absorbed by the PV cells and the generation of electron–hole pairs. Equation (4) describes the relationship between I_SC and solar irradiation (also shown in Figure 7).

$${\mathrm{I}}_{\mathrm{SC}}=155\times \left(\frac{G}{G_o}\right)+0.057.$$

(4)

Comparing the effect of increasing solar irradiation on V_OC and I_SC, as shown in Figure 6 and Figure 7, the effect on I_SC is greater, as the V_OC tends to reach a fixed value with increasing solar irradiation.

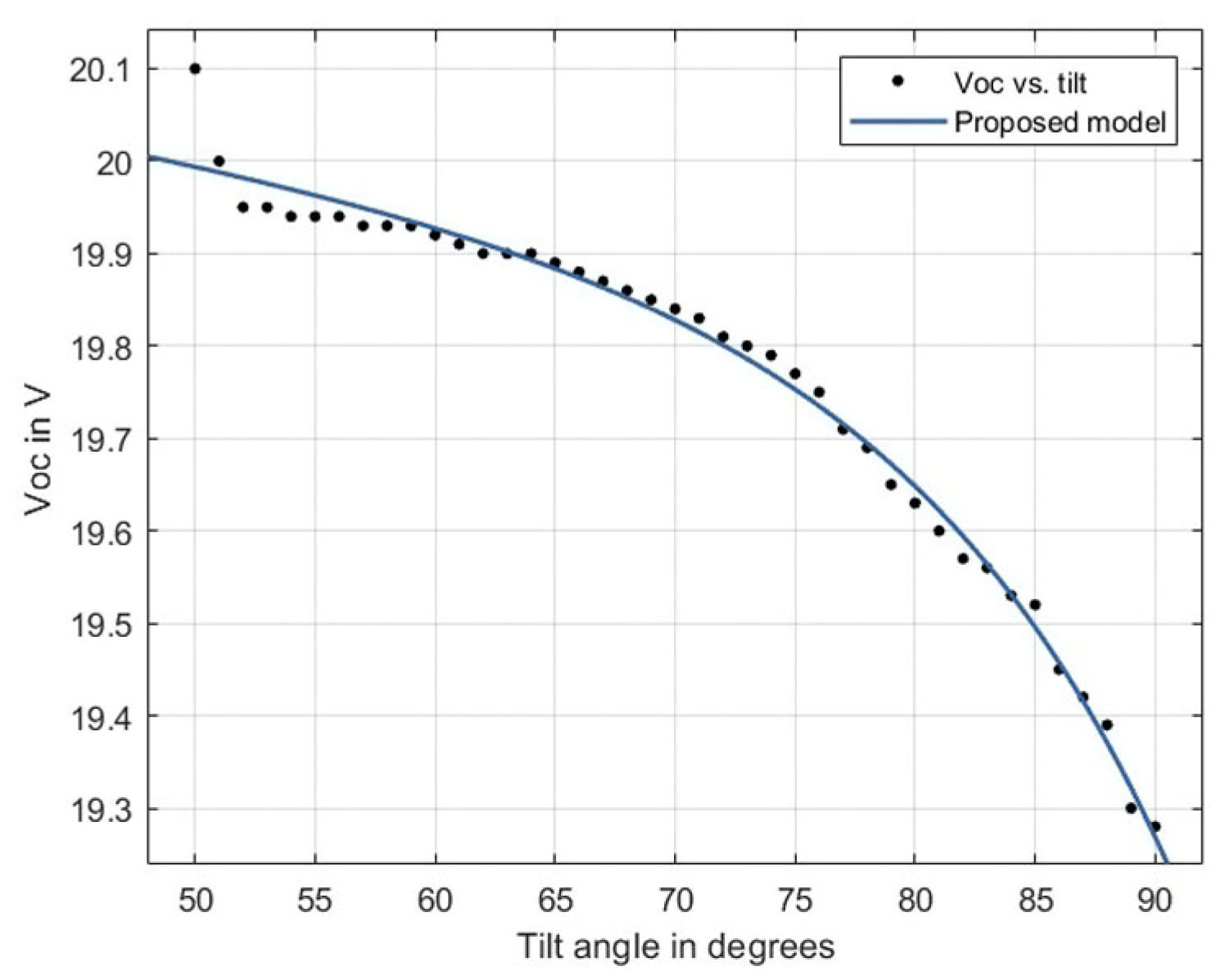
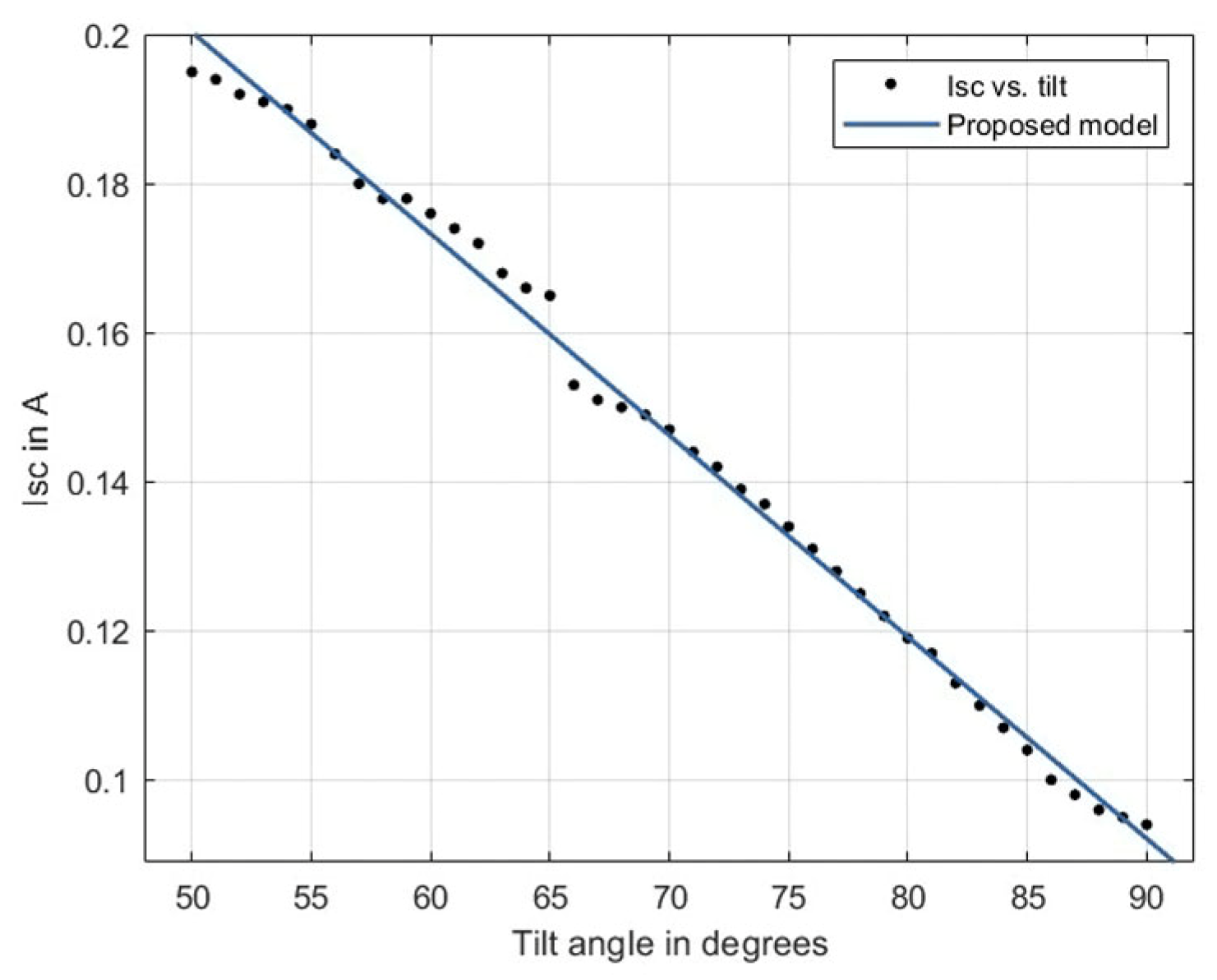
4.3. Modeling V_OC and I_SC with the Module Tilt Angle

The V_OC of a PV module can vary with changes in the module’s tilt angle θ. However, the effect of tilt angle on V_OC is relatively small compared to other factors such as temperature, the measurements taken at fixed azimuth angles and almost fixed module temperature Figure 8 shows the relationship between V_OC and the module tilt angle. These measurements were taken on Tuesday 27th of June, at noon, when the module was facing south. The model used to predict the values in Figure 8 is shown in Equation (5).

$$V_{OC} =-0.0002\times e^{5.18\times \mathsf{\theta }}+20.23\times e^{-0.0127\times \mathsf{\theta }},$$

(5)

where θ is the module tilt angle in radians.

The I_SC of a PV module is influenced by the module’s tilt angle. The I_SC tends to increase as the module tilt angle decreases from the system default, reaching its maximum value when the incoming sunlight is perpendicular to the module. Figure 9 describes the relationship between the I_SC and module tilt angle. The model used to describe Figure 9 is explained in Equation (6).

$$I_{SC}=-0.155\times \theta +0.333.$$

(6)

The relationship between I_SC and the tilt angle is linear for the window of tilt angles between 50° and 90°. However, according to [16] and Figure 7, the I_SC increases as solar irradiation increases, which makes Figure 9 correct, while if the tilt angle kept decreasing beyond 50° and reached an angle of 15°, the relationship would not be linear, as the I_SC would decrease.

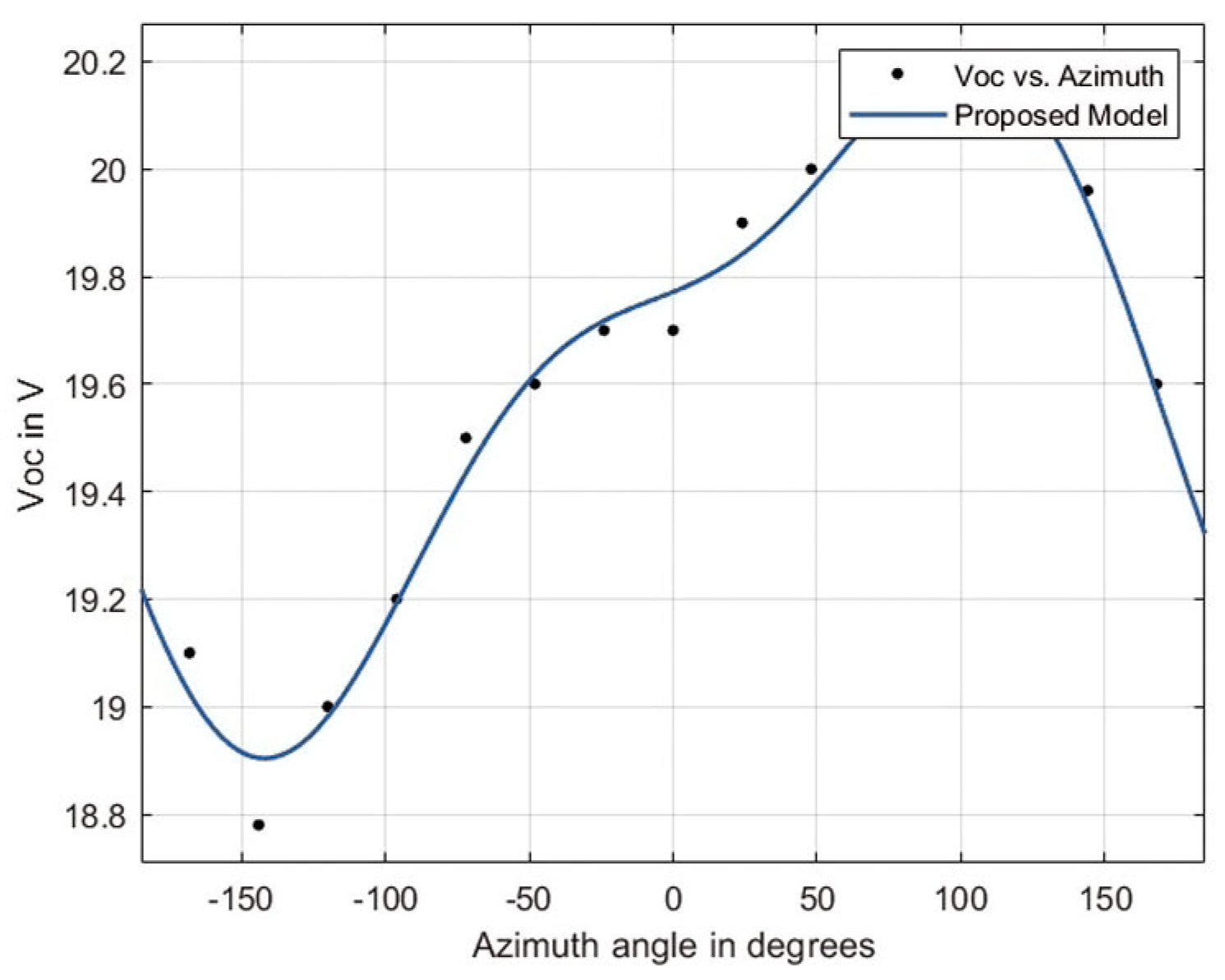
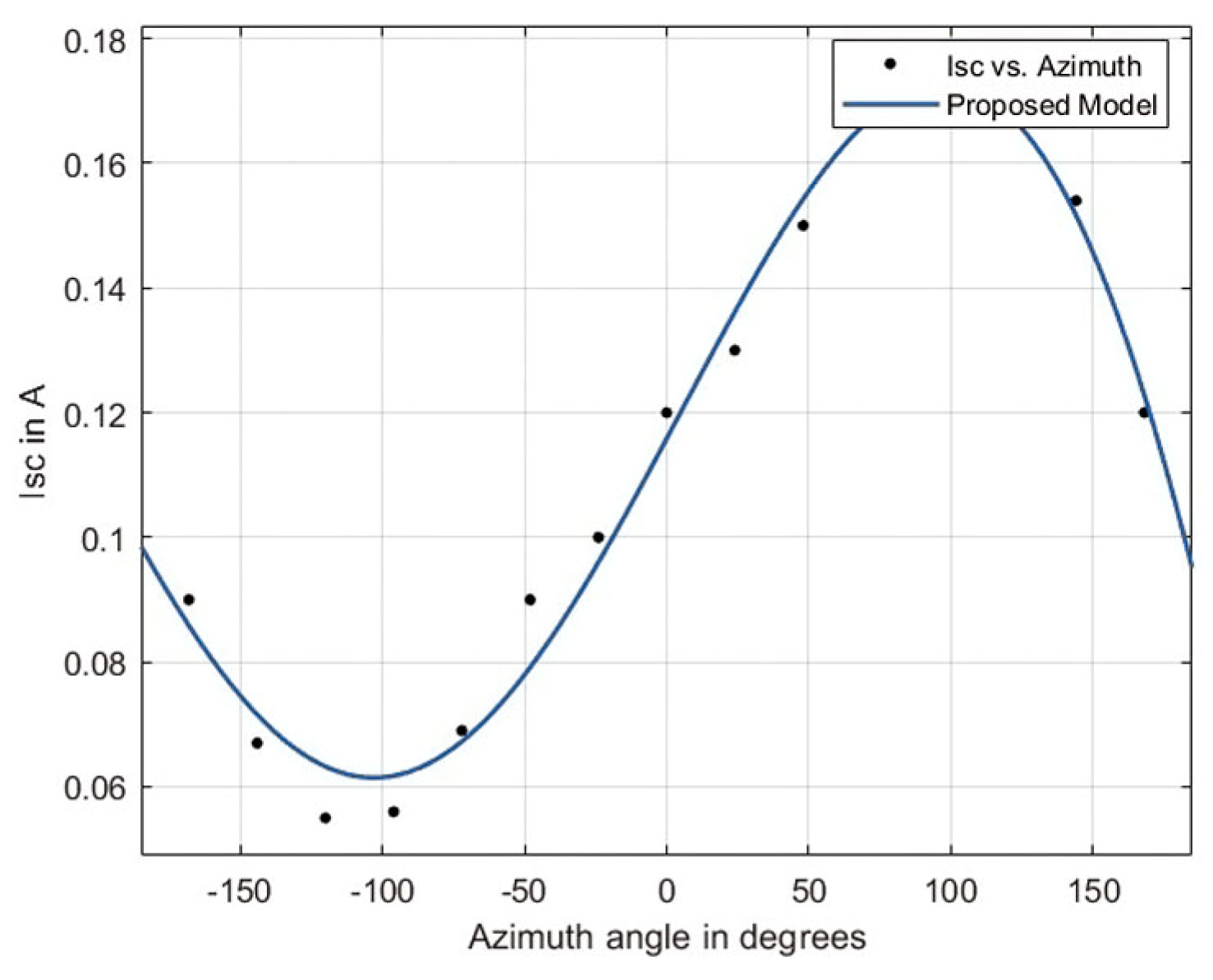
4.4. Modeling V_OC and I_SC with Azimuth Angle

The V_OC and I_SC of a photovoltaic (PV) module can be influenced by the azimuth angle ϕ, which represents the orientation of the module with respect to the sun’s position. The azimuth angle determines the angle at which sunlight hits the PV module. The measurements used in this study were taken at 14:00 at a fixed tilt angle of 60° and at an almost fixed temperature. Figure 10 and Figure 11 show the variation in V_OC and I_SC with the module azimuth angle. The models used to describe both relationships are shown in Equations (7) and (8), in which ϕ represents the azimuth angle in radians.

$$V_{OC}=19.6+0.25\cos \left(-0.955\times \mathsf{\varphi }\right)-0.49\sin \left(-0.955\times \mathsf{\varphi }\right)-0.09\cos \left(-1.9\times \mathsf{\varphi }\right)+0.18\sin \left(-1.9\times \mathsf{\varphi }\right).$$

(7)

$$I_{SC}=0.99\mathit{sin}\left(0.46\times \varphi +2.52\right)+0.93\mathit{sin}\left(0.52\times \varphi -0.51\right).$$

(8)

As shown in Figure 10 and Figure 11, each plot has a maximum and minimum point, and the location depends on the time of the day; here, the measurements took place at 14:00—that is the reason why the peak occurred in the west, while the trough occurred in the east.

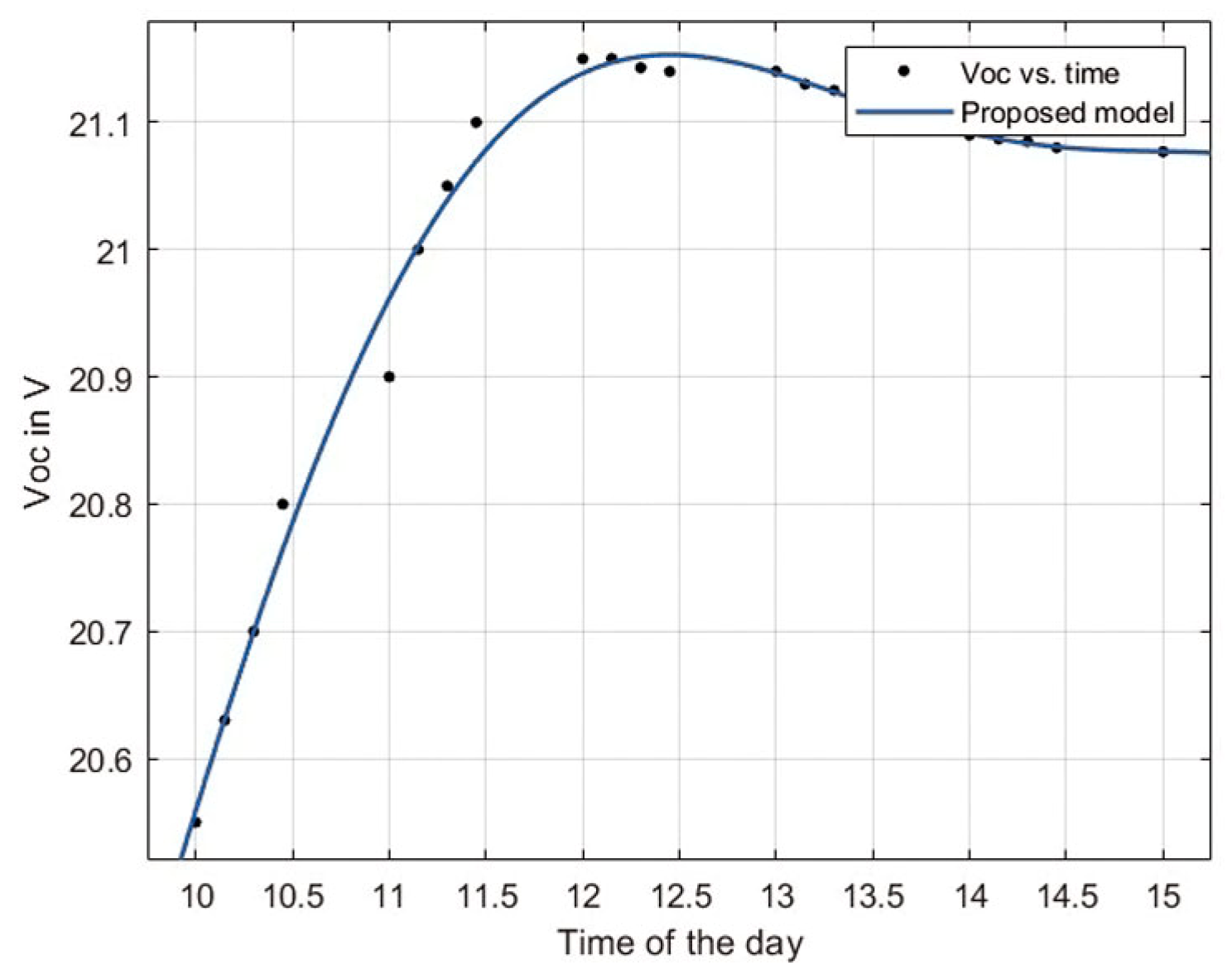
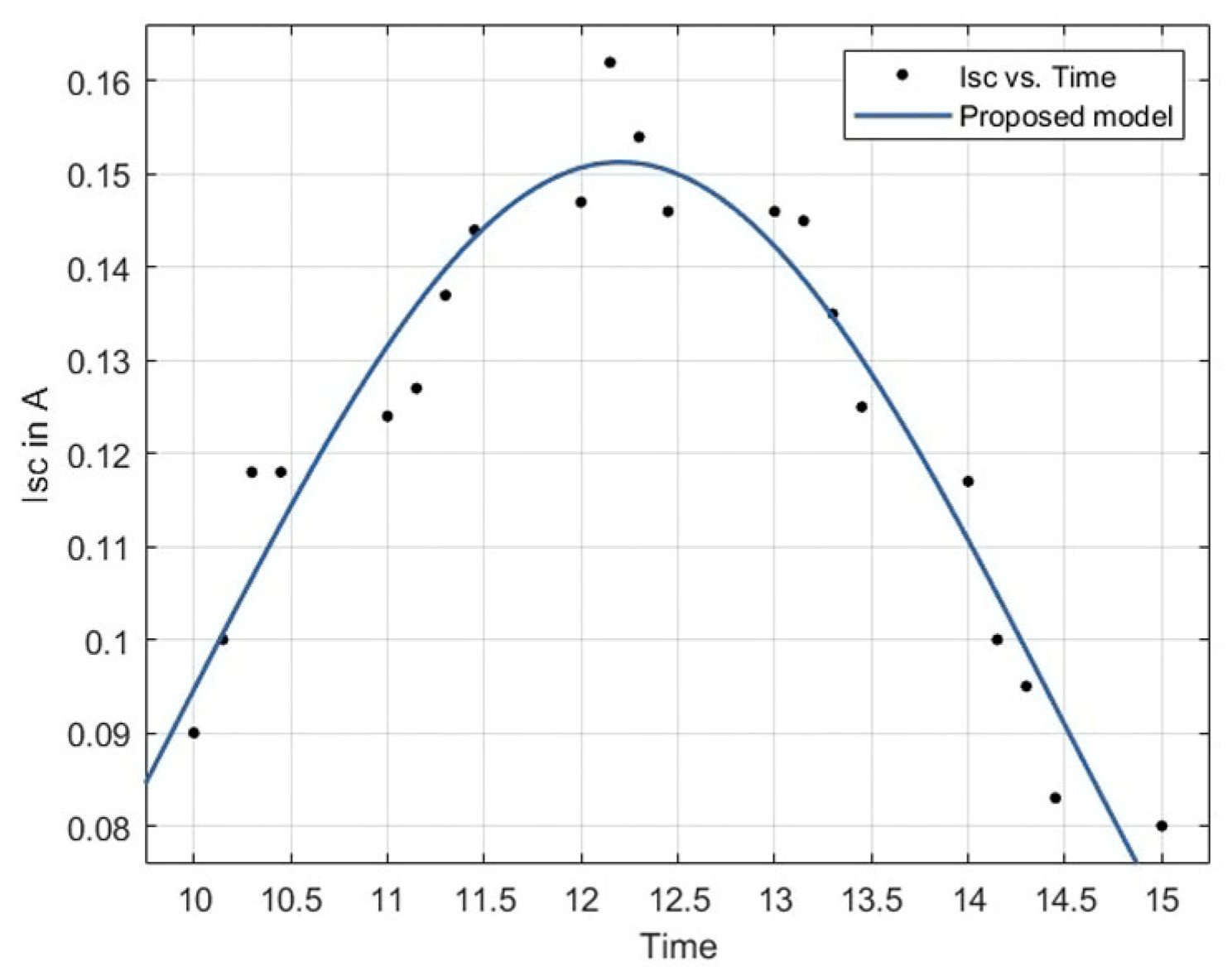
4.5. Modeling V_OC and I_SC with Time

The V_OC and I_SC of a photovoltaic (PV) module can vary with time due to various factors, such as changes in solar irradiance and temperature. In this model, the focus is only on when the solar irradiance changes as the time changes, considering an almost fixed module temperature, a tilt angle of 60°, and the direction the module was facing (in this case, south) as the key parameters; the measurements were taken 15 min at a time from 10:00 to 15:00. Figure 12 and Figure 13 show the variation in V_OC and I_SC with the time of the day, and Equations (9) and (10) illustrate the models describing V_OC and I_SC with time, respectively.

$$\begin{gathered} V_{OC}=20.56+0.766\mathit{cos}\left(5.56\ast \left[\frac{Time}{solarnoon}\right]\right)+0.136\mathit{sin}\left(5.56\ast \left[\frac{Time}{solarnoon}\right]\right) \\ -0.215\mathit{cos}\left(5.56\ast \left[\frac{Time}{solarnoon}\right]\right)-0.12\mathit{sin}\left(5.56\ast \left[\frac{Time}{solarnoon}\right]\right). \end{gathered}$$

(9)

$$I_{SC}=0.155\times e^{-{\left(\frac{\left[\frac{Time}{solarnoon}\right]-1.02}{0.27}\right)}^2},$$

(10)

where Time is the time of the day, and solarnoon is the noon time (12:00).

5. Conclusions

Solar energy harvesting using photovoltaic modules combined with an H-Darrius wind turbine is an effective and sustainable method of generating electricity. This study utilized five PV modules and took advantage of their self-cooling properties. The key factors of module temperature, tilt angle, azimuth angle, solar irradiation, and daytime were measured to model each factor independently using a single PV module. The V_OC and I_SC of the entire system were then measured at various tilt angles and module temperatures. This approach proved to be successful in estimating V_OC and I_SC with acceptable error.

To further enhance the system’s performance, it is important to consider the integration of wind turbine output. This would allow for accurate measurements of the total power generated by the system. Additionally, studying the impact of wind speed on the wind turbine’s power output, as well as monitoring the V_OC and I_SC of the module, would provide valuable insights for future improvements.