Research on INS/GNSS/UWB Adaptive Robust ESKF Kinematic and Static Filtering Based on Cost Function †
Abstract
1. Introduction
2. Kinematic and Static Filtering Based on the ESKF
2.1. ESKF Fundamentals
2.1.1. ESKF Kinematic Models
2.1.2. ESKF State-Prediction Model
2.1.3. ESKF Measurement-Prediction Model
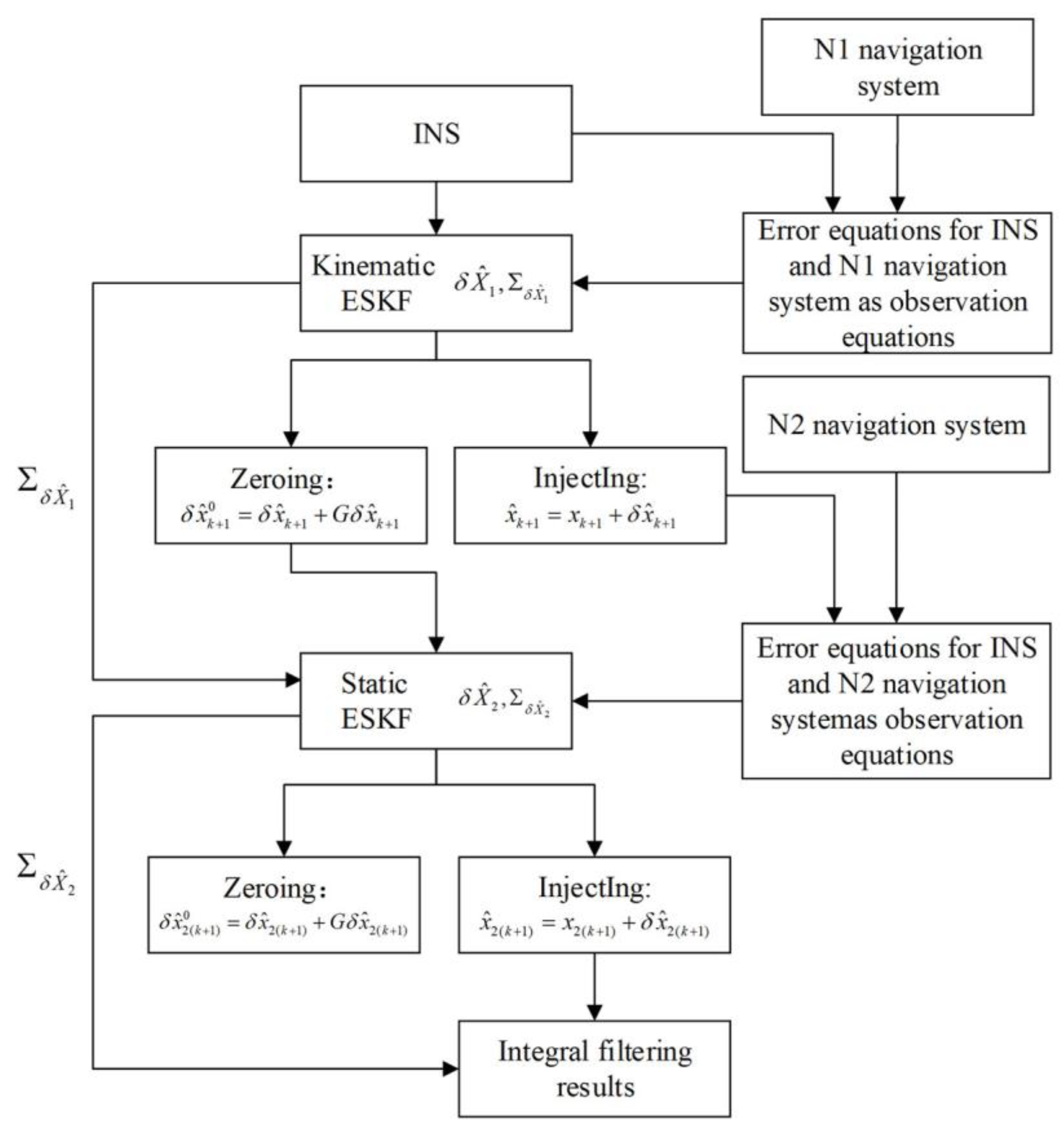
2.2. Kinematic and Static Filter Structure Based on ESKF
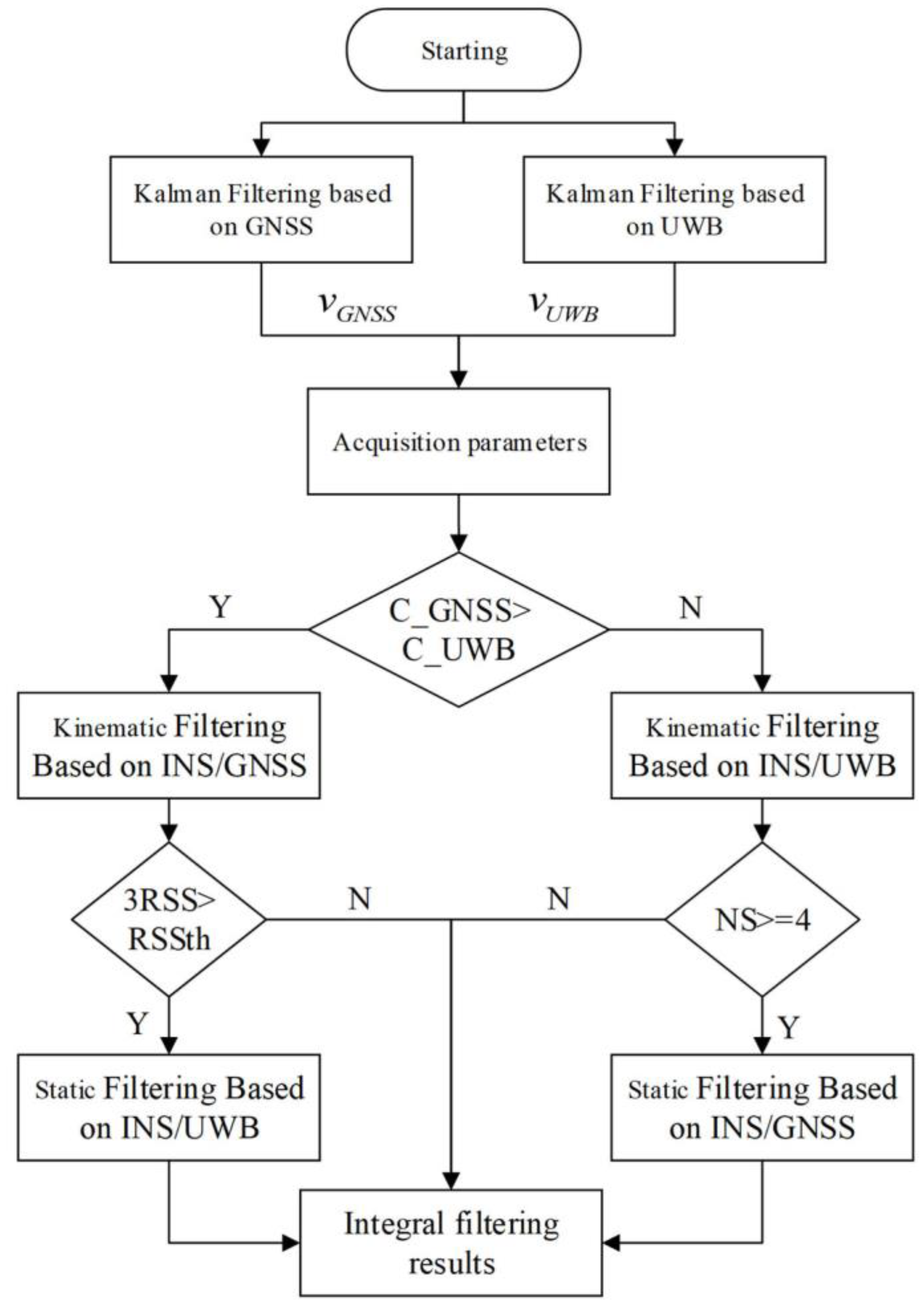
3. INS/GNSS/UWB Adaptive Robust ESKF Kinematic and Static Filtering Based on Cost Function
3.1. Switching Algorithm Based on Cost Function
- Normalization: Normalizing each column vector of matrix yields: .
- Summation: Summing by rows gives: .
- Obtaining the power vector: Normalizing to yields a power vector: .
3.2. Integral Filter Structure
4. Simulation Experiment and Result Analysis
4.1. Trajectory Simulation and Parameter Settings
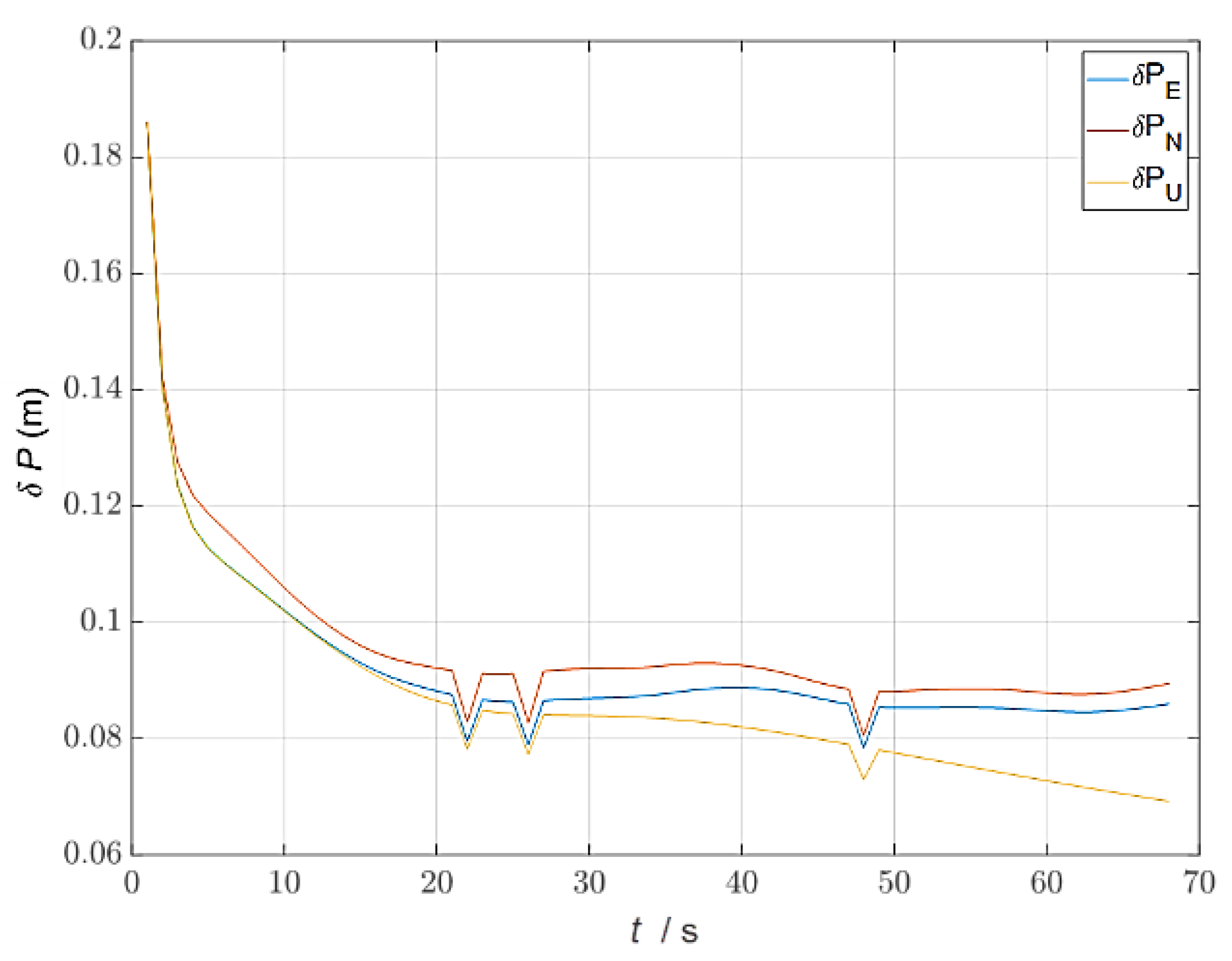
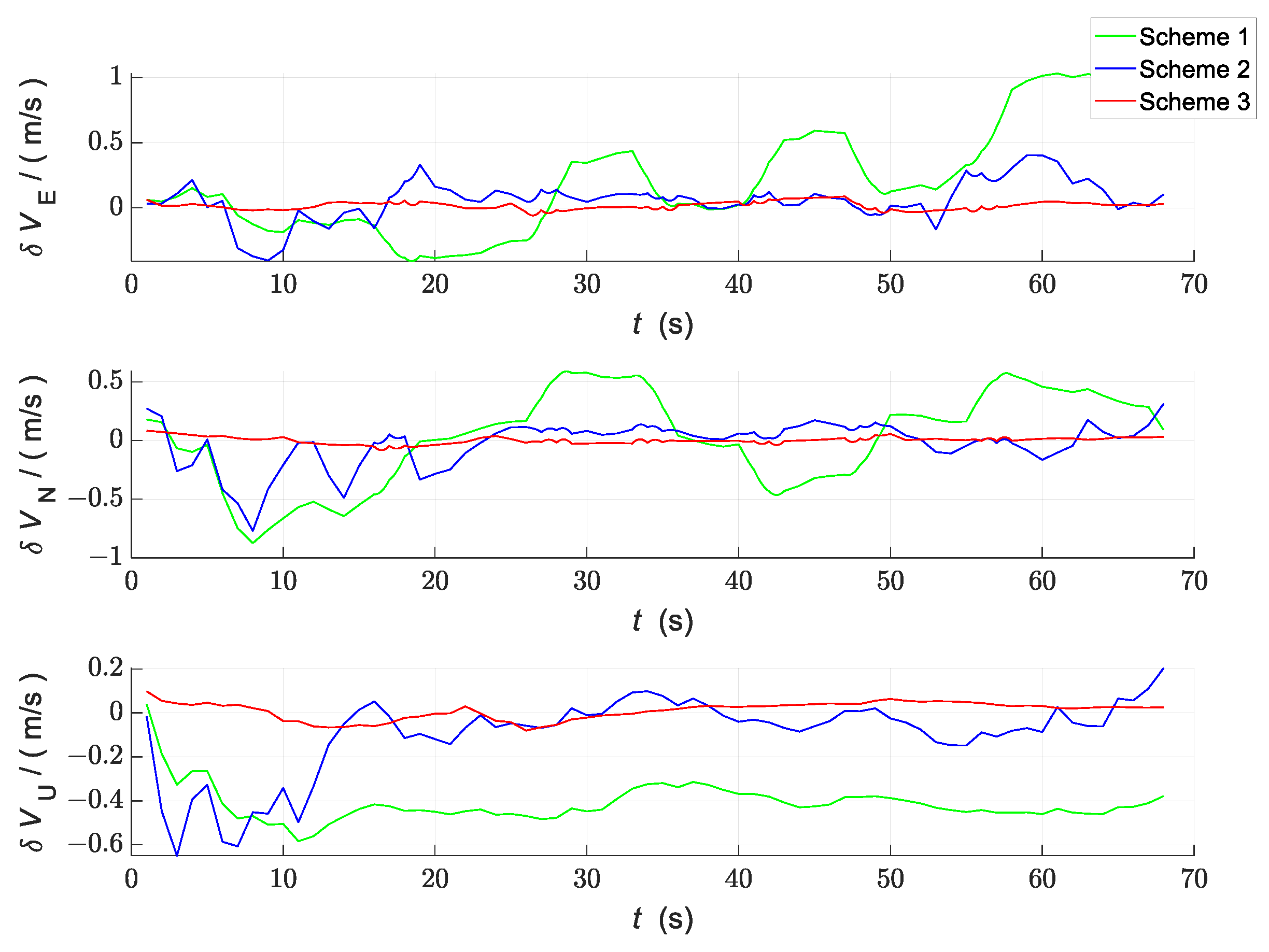
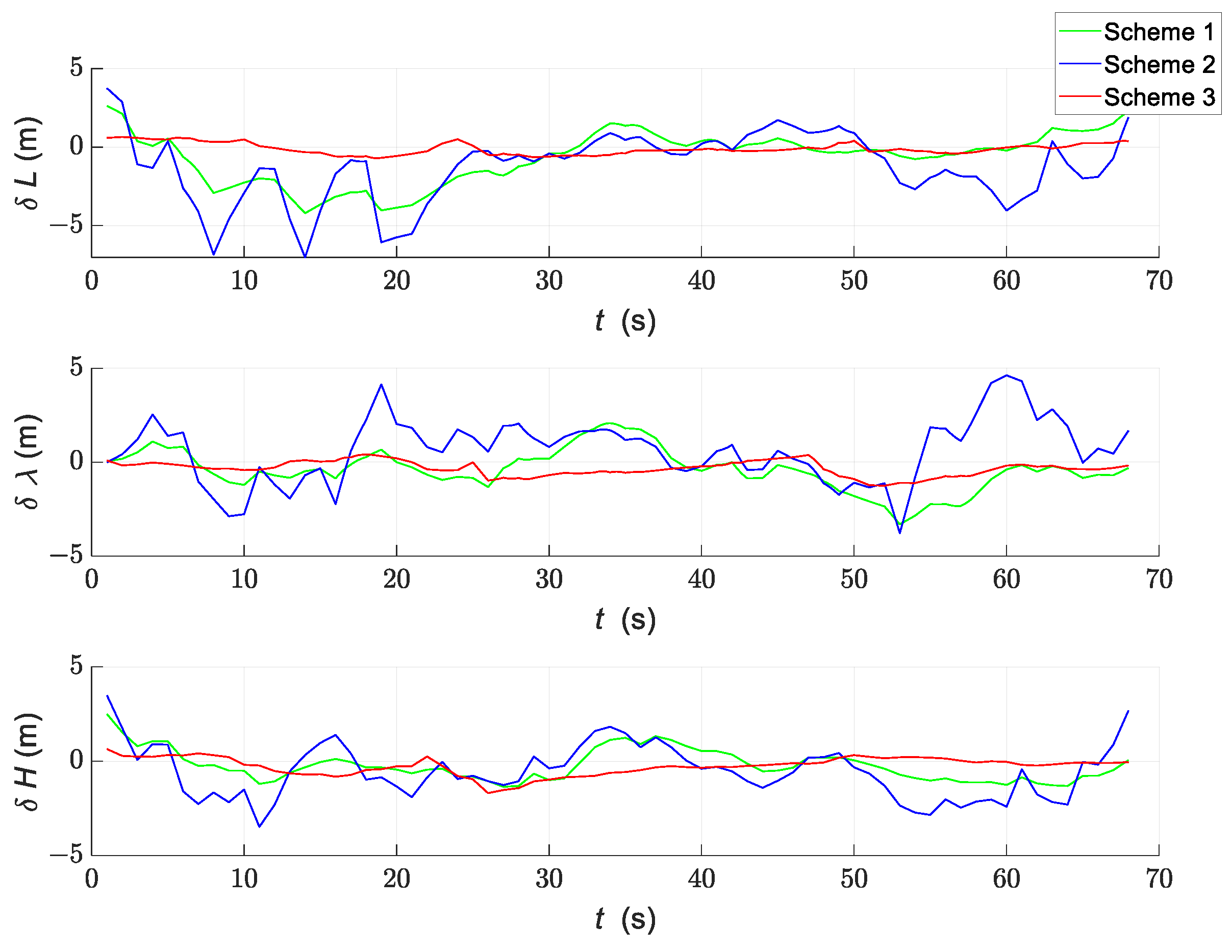
4.2. Simulation Results and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wei, W. Research on Basic Characteristics of Multi-source Autonomous Navigation System. J. Astronaut. 2023, 44, 519–529. [Google Scholar]
- Wang, W.; Wu, Z.; Meng, F.; Xu, X.; Wu, S. Research on Dependability of Multi-source Autonomous Navigation System. Navig. Control 2023, 22, 1–9. [Google Scholar]
- Shen, C.; Wang, C.; Zhang, K.; Wang, X.; Liu, J. A time difference of arrival/angle of arrival fusion algorithm with steepest descent algorithm for indoor non-line-of-sight locationing. Int. J. Distrib. Sens. Netw. 2019, 15, 1550147719860354. [Google Scholar] [CrossRef]
- García, E.; Poudereux, P.; Hernández, Á.; Ureña, J.; Gualda, D. A Robust UWB Indoor Positioning System for Highly Complex Environments. In Proceedings of the IEEE International Conference on Industrial Technology, ICIT 2015, Seville, Spain, 17–19 March 2015; pp. 3386–3391. [Google Scholar]
- Kuang, J.; Niu, X.; Chen, X. Robust Pedestrian Dead Reckoning Based on MEMS-IMU for Smartphones. Sensors 2018, 18, 1391. [Google Scholar] [CrossRef] [PubMed]
- René, H. Seamless Indoor/Outdoor Positioning Handover for Location-Based Services in Streamspin. In Proceedings of the Tenth International Conference on Mobile Data Management: Systems, Services and Middleware, Taipei, Taiwan, 18–20 May 2009; pp. 267–272. [Google Scholar]
- Yang, F.; Aoshuang, D. A Solution of Ubiquitous Location Based on GPS and Wi-Fi ULGW. In Proceedings of the Ninth International Conference on Hybrid Intelligent Systems, Shenyang, China, 12–14 August 2009; pp. 260–263. [Google Scholar] [CrossRef]
- Deng, Z.; Zhu, Y.; Wang, H. Cost Function of Features Based Mode Switching Algorithm for Indoor Positioning. In Proceedings of the 5th International Conference on Wireless Communications, Networking and Mobile Computing, Beijing, China, 24–26 September 2009; pp. 1–4. [Google Scholar]
- Wu, M. Research of Handover Algorithm Based on Fuzzy Logic Control For Seamless Navigation System; Harbin Institute of Technology: Harbin., China, 2012. [Google Scholar]
- Hassen, W.; Najjar, F. A Positioning Technology Switch Algorithm for Ubiquitous Pedestrian Navigation Systems. In Proceedings of the IEEE 13th International Conference on Embedded and Ubiquitous Computing, Porto, Portugal, 21–23 October 2015; pp. 124–131. [Google Scholar] [CrossRef]
- Ren, Z.; Liu, S.; Dai, J.; Lv, Y.; Fan, Y. Research on Kinematic and Static Filtering of the ESKF Based on INS/GNSS/UWB. Sensors 2023, 23, 4735. [Google Scholar] [CrossRef] [PubMed]
- Yorozu, T.; Hirano, M.; Oka, K.; Tagawa, Y. Electron Spectroscopy Studies on Magneto-Optical Media and Plastic Substrate Interface. IEEE Transl. J. Magn. Jpn. 1987, 2, 740–741. [Google Scholar] [CrossRef]
- Zhenyao, L. Research on Technology of Seamless Positioning Based-on UWB/GNSS/MIMU; Information Engineering University: Henan, China, 2017. [Google Scholar]



| Weight Values of Parameters | RSS | Positioning Residual | Received Signal Stability |
|---|---|---|---|
| RSS | 1 | 3 | 5 |
| Positioning residual | 1/3 | 1 | 3 |
| Received signal stability | 1/5 | 1/3 | 1 |
| Trajectory Segment | Timing, s | Items of Change | Region of Carrier |
|---|---|---|---|
| Rest | 0–5 | Ins performed rough calibration. | Outdoor |
| Carrier acceleration | 5–7 | Uniformly accelerated linear motion with an acceleration magnitude of 0.5 m/s2. | Outdoor |
| Running at uniform speed | 7–15 | Moving northward in a straight line at a uniform speed of 1 m/s. | Outdoor |
| Turning | 15–20 | Turn 90° from north to east | Outdoor |
| Running at uniform speed | 20–25 | Moving eastward in a straight line at a uniform speed of 1 m/s. | 20 s–23 s in outdoor, 23 s–25 s in indoor-outdoor transition area |
| Turning | 25–30 | –Turn 90° from east to south | 25 s–27 s in indoor-outdoor transition area, 27 s–30 s in indoor |
| Running at uniform speed | 30–32 | Moving southward in a straight line at a uniform speed of 1 m/s. | Indoor |
| Turning | 32–37 | Turn 90° from south to east | Indoor |
| Running at uniform speed | 37–39 | Moving eastward in a straight line at a uniform speed of 1 m/s. | Indoor |
| Turning | 39–44 | Turn 90° from east to north | Indoor |
| Running at uniform speed | 44–46 | Moving north ward in a straight line at a uniform speed of 1 m/s. | Indoor |
| Turning | 46–51 | Turn 90° from north to east | 46 s–49 s in indoor, 49 s–51 s in indoor-outdoor transition area |
| Running at uniform speed | 51–54 | Moving eastward in a straight line at a uniform speed of 1 m/s. | 51 s–53 s in outdoor |
| Turning | 54–59 | Turn 90° from east to south | Outdoor |
| Running at uniform speed | 59–67 | Moving southward in a straight line at a uniform speed of 1 m/s. | Outdoor |
| Carrier deceleration | 67–69 | Uniformly decelerated linear motion with an acceleration magnitude of −0.5 m/s2. | Outdoor |
| Sensor Type | Parameter | Value | Value |
|---|---|---|---|
| IMU | Gyro error | Bias | [0.2°/h; 0.2°/h; 0.2°/h] |
| Random walking error | 0.08°/ | ||
| Accelerometer error | Bias | [100 μg; 100 μg; 100 μg] | |
| Random walking error | 20 μg/ | ||
| GNSS | Location | [0.5 m; 0.5 m; 0.5 m] | |
| Speed | 0.1 m/s | ||
| Frequency | 1 Hz | ||
| UWB | Location | [0.4 m; 0.4 m; 0.4 m] | |
| Speed | 0.1 m/s | ||
| Frequency | 1 Hz | ||
| RMSE | VX (m/s) | VY (m/s) | VZ (m/s) | X (m) | Y (m) | Z (m) |
|---|---|---|---|---|---|---|
| Scheme 1 | 0.47 | 0.39 | 0.42 | 1.73 | 1.41 | 0.82 |
| Scheme 2 | 0.16 | 0.19 | 0.20 | 2.46 | 2.13 | 1.42 |
| Scheme 3 | 0.03 | 0.03 | 0.04 | 0.37 | 0.63 | 0.54 |
| MAE | VX (m/s) | VY (m/s) | VZ (m/s) | X (m) | Y (m) | Z (m) |
|---|---|---|---|---|---|---|
| Scheme 1 | 0.35 | 0.33 | 0.42 | 1.28 | 1.09 | 0.70 |
| Scheme 2 | 0.12 | 0.13 | 0.13 | 1.83 | 1.74 | 1.18 |
| Scheme 3 | 0.03 | 0.02 | 0.04 | 0.32 | 0.51 | 0.40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, Z.; Liu, S.; Liu, J.; Dai, J.; Lv, Y. Research on INS/GNSS/UWB Adaptive Robust ESKF Kinematic and Static Filtering Based on Cost Function. Eng. Proc. 2024, 60, 8. https://doi.org/10.3390/engproc2024060008
Ren Z, Liu S, Liu J, Dai J, Lv Y. Research on INS/GNSS/UWB Adaptive Robust ESKF Kinematic and Static Filtering Based on Cost Function. Engineering Proceedings. 2024; 60(1):8. https://doi.org/10.3390/engproc2024060008
Chicago/Turabian StyleRen, Zongbin, Songlin Liu, Jing Liu, Jun Dai, and Yunzhu Lv. 2024. "Research on INS/GNSS/UWB Adaptive Robust ESKF Kinematic and Static Filtering Based on Cost Function" Engineering Proceedings 60, no. 1: 8. https://doi.org/10.3390/engproc2024060008
APA StyleRen, Z., Liu, S., Liu, J., Dai, J., & Lv, Y. (2024). Research on INS/GNSS/UWB Adaptive Robust ESKF Kinematic and Static Filtering Based on Cost Function. Engineering Proceedings, 60(1), 8. https://doi.org/10.3390/engproc2024060008






