Domination Number in the Context of Some New Graphs †
Abstract
:1. Introduction
2. Definitions
3. Main Results
- Condition I: n ≡ 0 mod5, γ(G) = 0.4n is the domination number.
- Condition II: n ≡ 1 mod5, γ(G) = ⌈0.4n + 0.6⌉ is the domination number.
- Condition III: n ≡ 2 mod5, γ(G) = ⌊0.4n + 0.5⌋ is the domination number.
- Condition IV: n ≡ 3 mod5, γ(G) = 0.4n + 0.8 is the domination number.
- Condition V: n ≡ 4 mod5, γ(G) = ⌊0.4n + 0.8⌋ is the domination number. □
- (1)
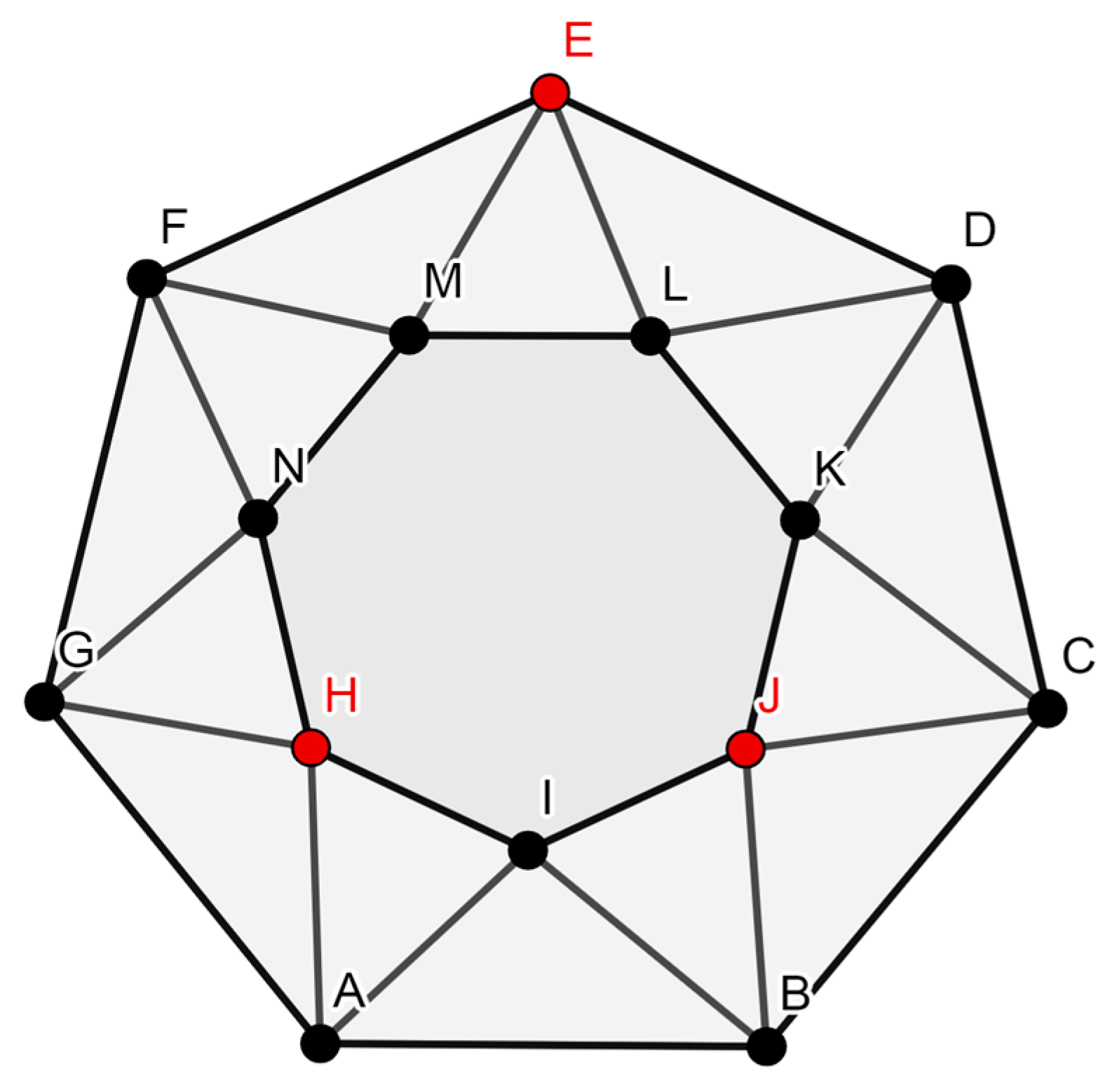
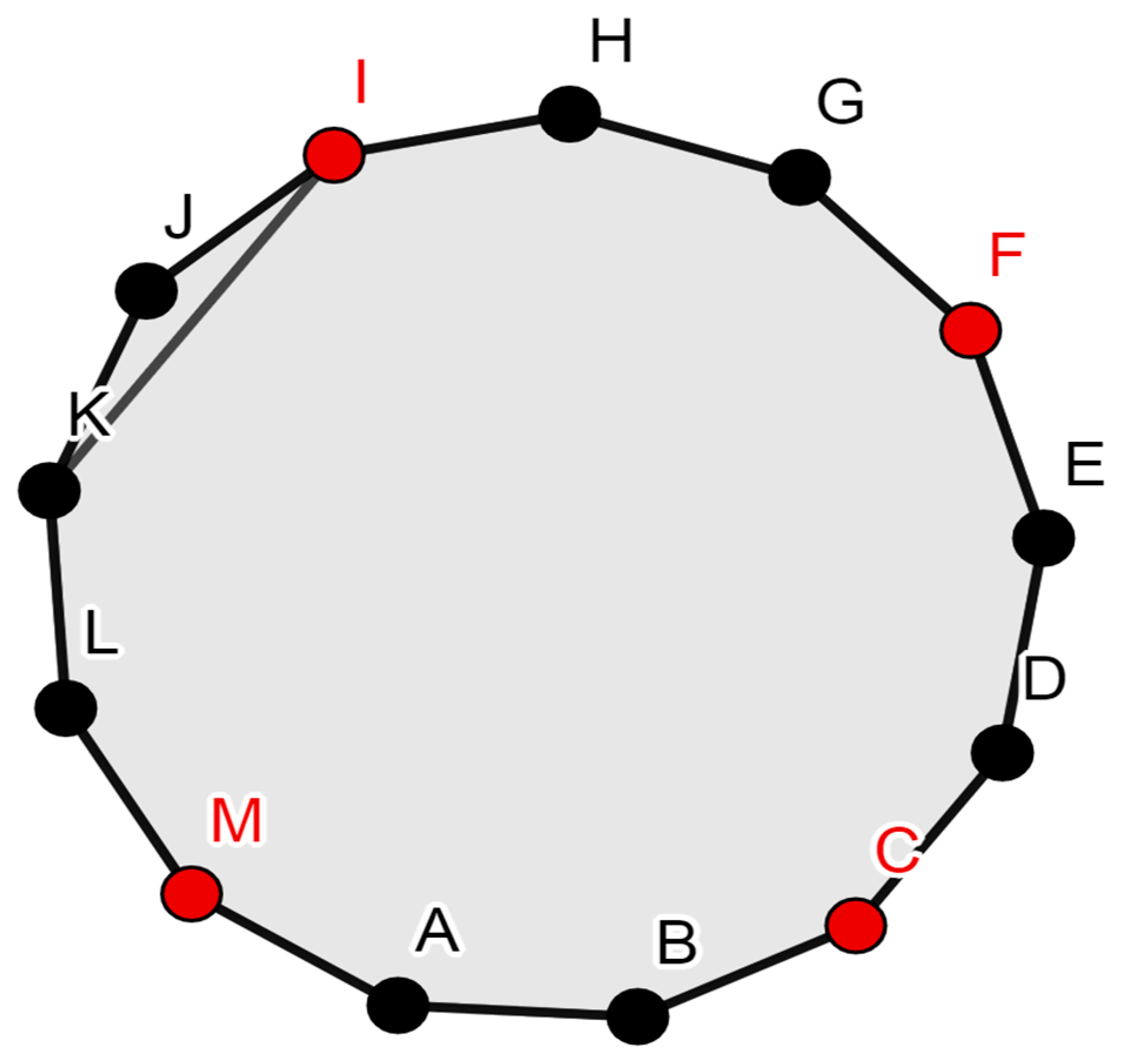
- The domination number of an antiprism graph A7 is 3, as shown in Figure 1.
- (2)
- The domination number of an antiprism graph A10 is 4, as shown in Figure 2.
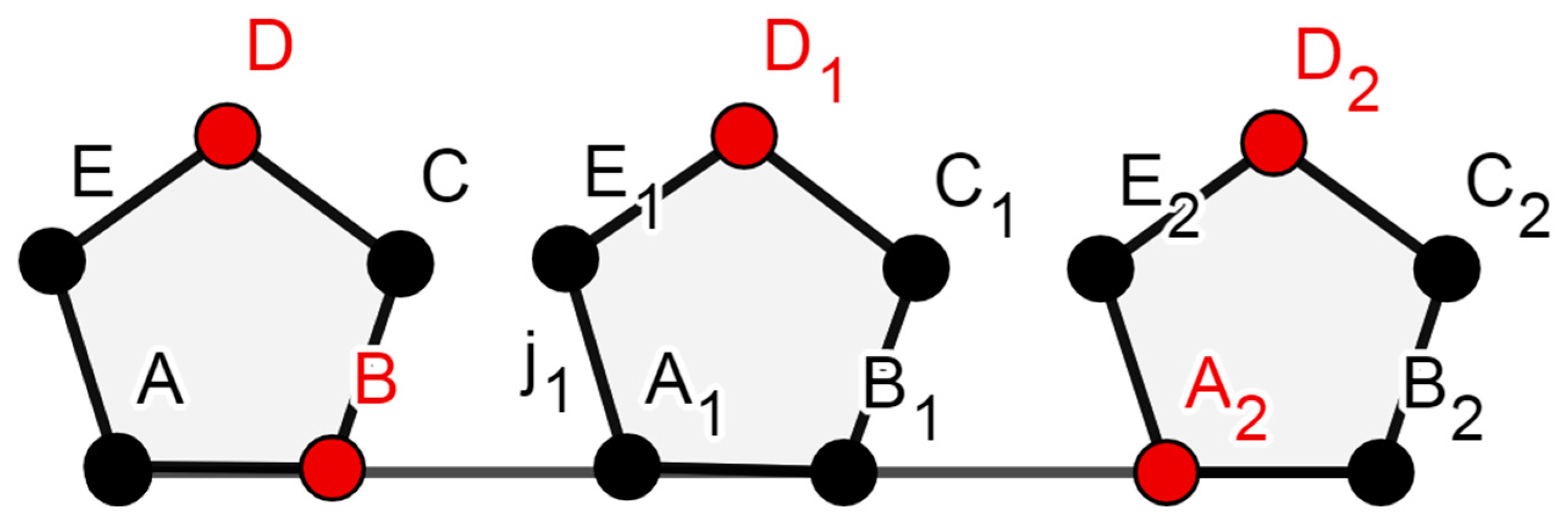
- Condition I: n ≡ 0 mod3, γ(G) = ⌊⌋ is the domination number.
- Condition II: n ≡ 1 mod3, γ(G) = + is the domination number.
- Condition III: n ≡ 2 mod3, γ(G) = + is the domination number. □
- (1)
- (2)
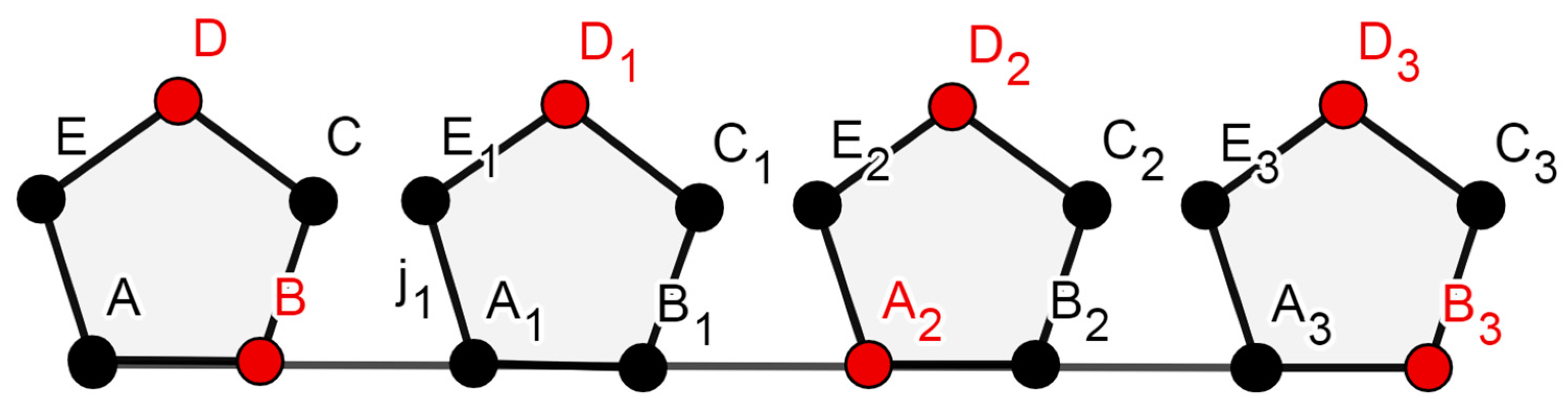
- Condition I: n ≡ 0 mod3, γ(G) = is the domination number.
- Condition II: n ≡ 1 mod3, γ(G) = − is the domination number.
- Condition III: n ≡ 2 mod3, γ(G) = + is the domination number. □
- (1)
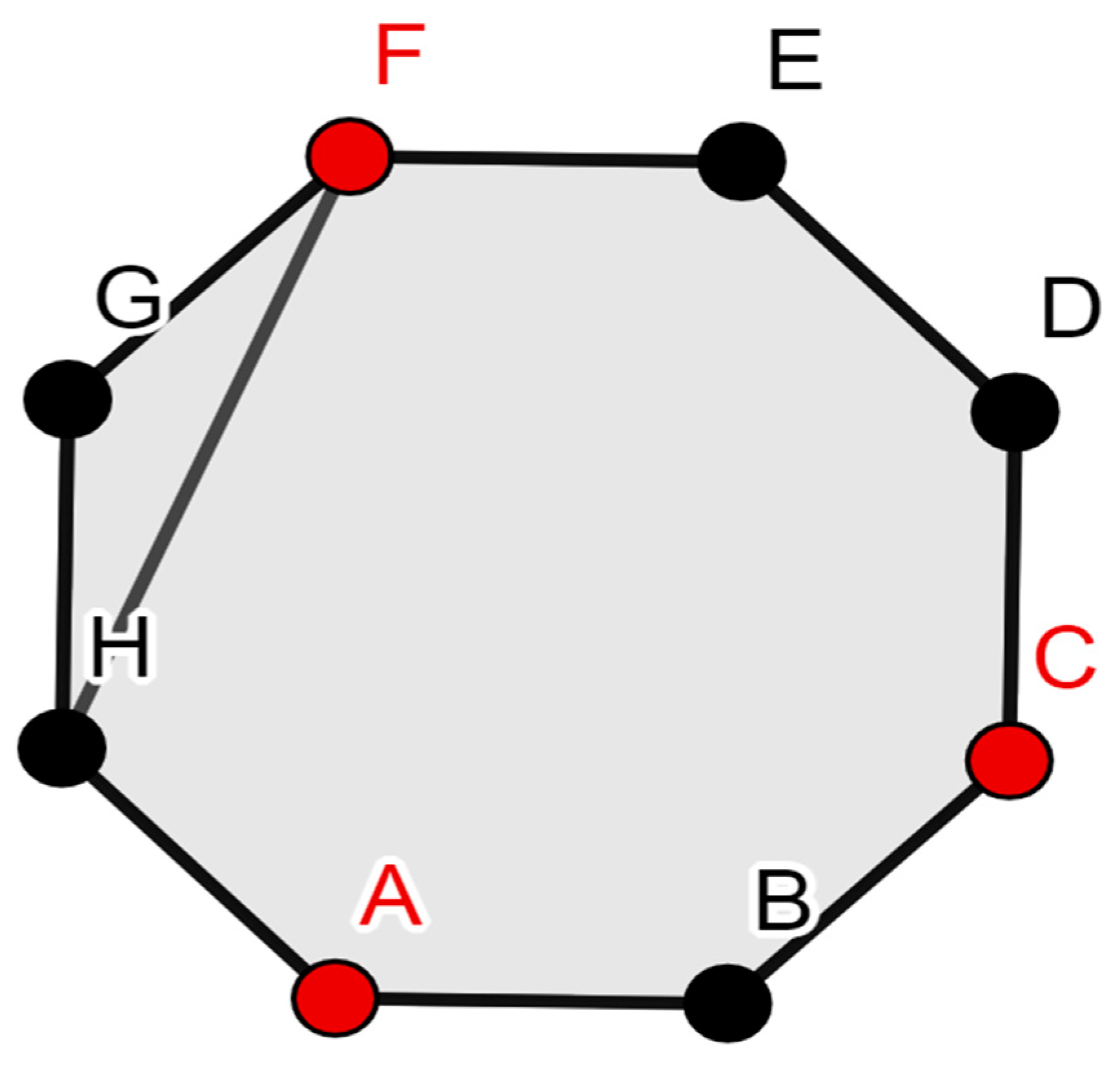
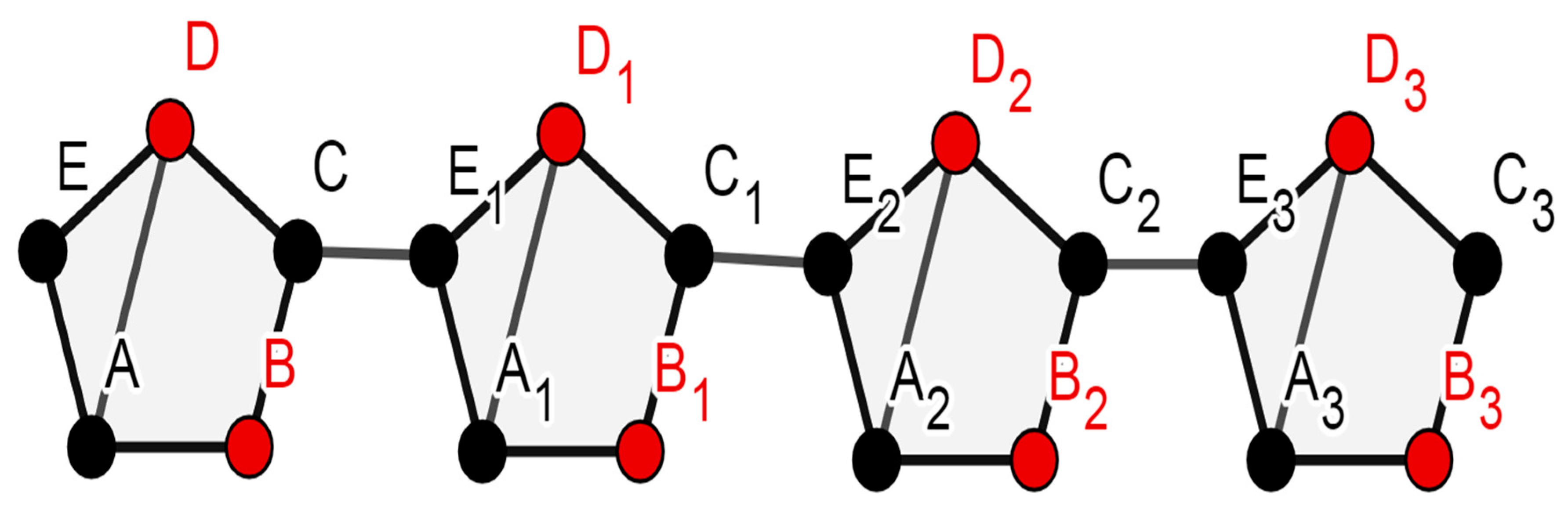
- The domination number of a cycle C8 with one chord is 3, as shown in Figure 5.
- (2)
- The domination number of a cycle C13 with one chord is 4, as shown in Figure 6.
- Condition I: n ≡ 0 mod3, γ(G) = m is the domination number.
- Condition II: n ≡ 1 mod3, γ(G) = ( − )m is the domination number.
- Condition III: n ≡ 2 mod3, γ(G) = ( + )m is the domination number. □
- (1)
- (2)
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ambily, S.; Sebastian, B.; Varghese, L.A. Domination in Graphs. Int. J. Mod. Trends Eng. Res. (IJMTER) 2016, 3, 135–141. [Google Scholar]
- Gupta, P. Domination in Graph with Application. Paripex Indian J. Res. 2013, 2, 115–117. [Google Scholar]
- Jayachandran, E.; Sugumaran, A. Domination number of some graphs. Int. J. Sci. Dev. Res. 2018, 3, 386–391. [Google Scholar]
- Vaidya, S.K.; Karkar, S.H. On Strong Domination Number of Graphs. Appl. Appl. Math. Int. J. (AAM) 2017, 12, 604–612. [Google Scholar]
- Abdul, R.; Meenakshi, S.; Tamiloli, P. Independent Domination Number for 6- Alternative Snake graphs. J. Algebr. Stat. 2022, 13, 1887–1890. [Google Scholar]
- Meenakshi, S.; Senthurpriya, N. Independent Domination Number in Triangular and Quadrilateral Snake Graph. Int. J. Recent Technol. Eng. (IJRTE) 2019, 8, 20–23. [Google Scholar]
- Sadawarte, S.; Srivastav, S. Signed product cordial labeling of some pan graphs. Mater. Today Proc. 2022, 57, 2307–2310. [Google Scholar] [CrossRef]
- Sadawarte, S.; Srivastav, S. On Signed Product Cordial Labeling of Some Square Cycle Graphs. Des. Eng. 2021, 57, 13228–13233. [Google Scholar]
- Bhuvaneswari, D.; Meenakshi, S. Domination Integrity of Snake and Sunlet Graphs. Adv. Appl. Math. Sci. 2021, 20, 1811–1821. [Google Scholar]
- Adawiyah, R.; Agustin, I.H.; Dafik; Slamin; Albirri, E.R. Related Wheel Graphs and Its Locating Edge Domination Number. J. Phys. 2018, 1022, 012007. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leel, S.; Srivastav, S.; Gupta, S.; Ganesan, G. Domination Number in the Context of Some New Graphs. Eng. Proc. 2024, 62, 14. https://doi.org/10.3390/engproc2024062014
Leel S, Srivastav S, Gupta S, Ganesan G. Domination Number in the Context of Some New Graphs. Engineering Proceedings. 2024; 62(1):14. https://doi.org/10.3390/engproc2024062014
Chicago/Turabian StyleLeel, Slashi, Sweta Srivastav, Sangeeta Gupta, and Geetha Ganesan. 2024. "Domination Number in the Context of Some New Graphs" Engineering Proceedings 62, no. 1: 14. https://doi.org/10.3390/engproc2024062014
APA StyleLeel, S., Srivastav, S., Gupta, S., & Ganesan, G. (2024). Domination Number in the Context of Some New Graphs. Engineering Proceedings, 62(1), 14. https://doi.org/10.3390/engproc2024062014





