Impact of Climate Change on the Thermoeconomic Performance of Binary-Cycle Geothermal Power Plants †
Abstract
:1. Introduction
2. Methods
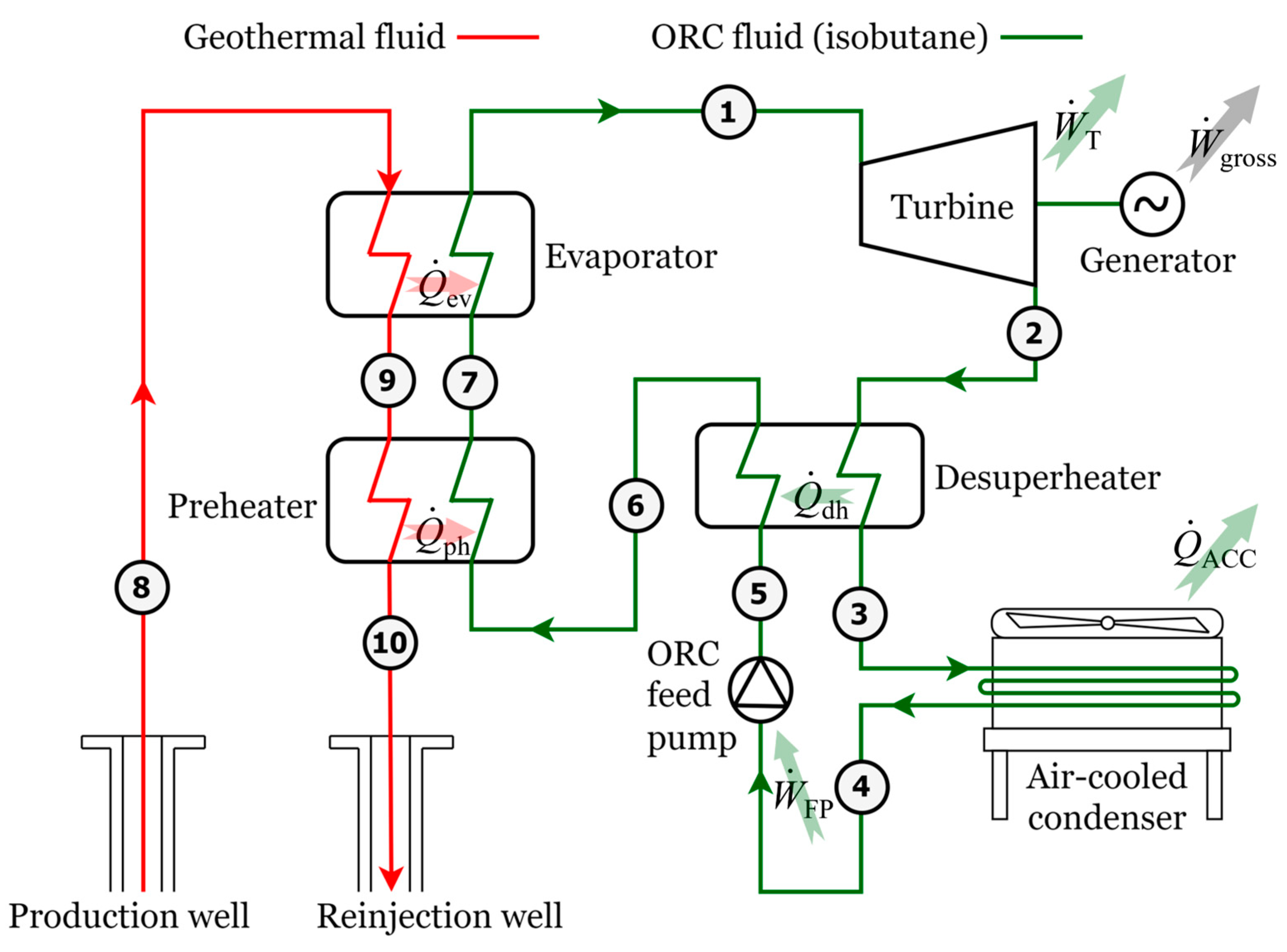
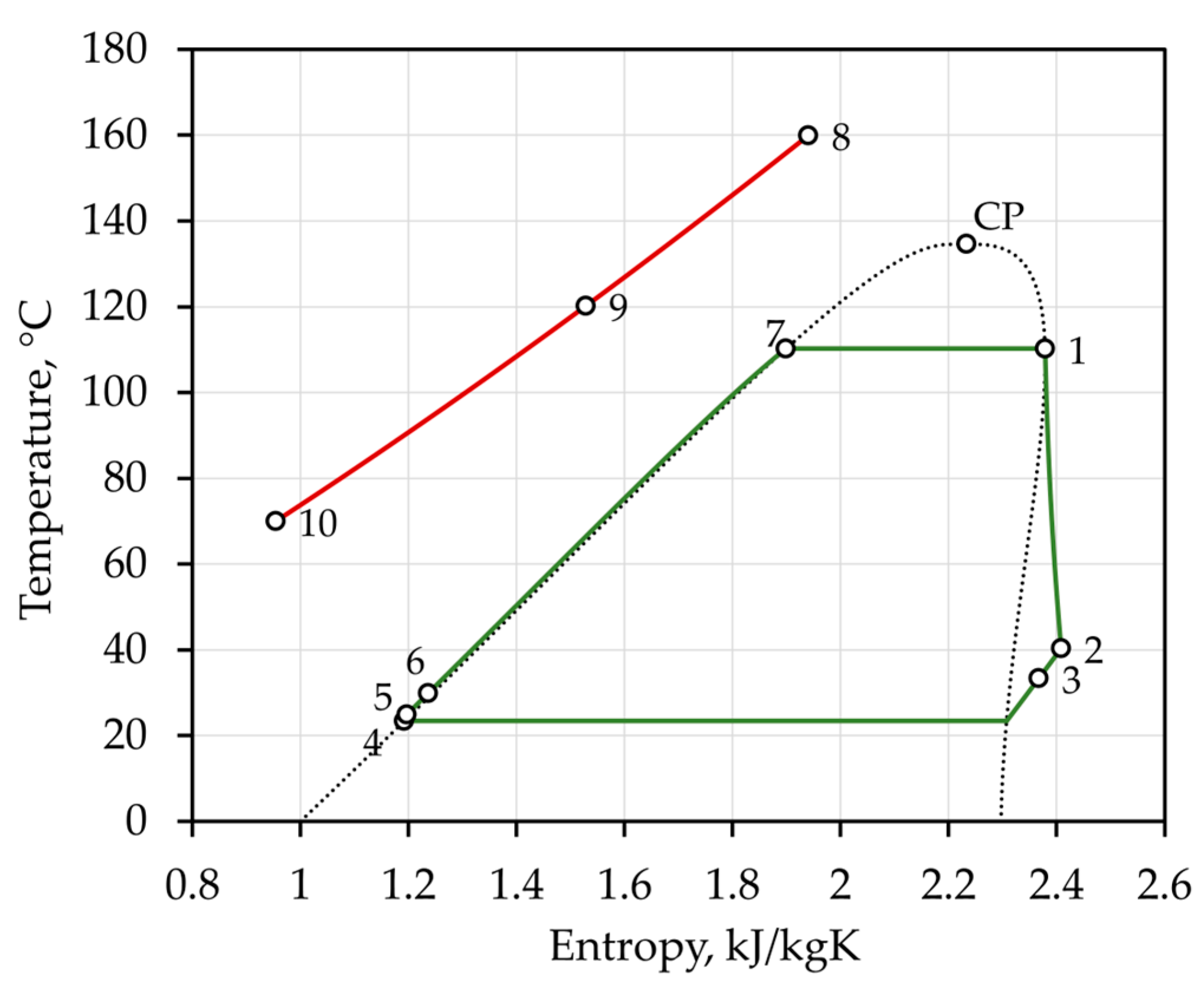
2.1. Thermodynamic Model
2.2. Climate Data
3. Results and Discussion
3.1. Comparison between Observed and Predicted Air Temperatures
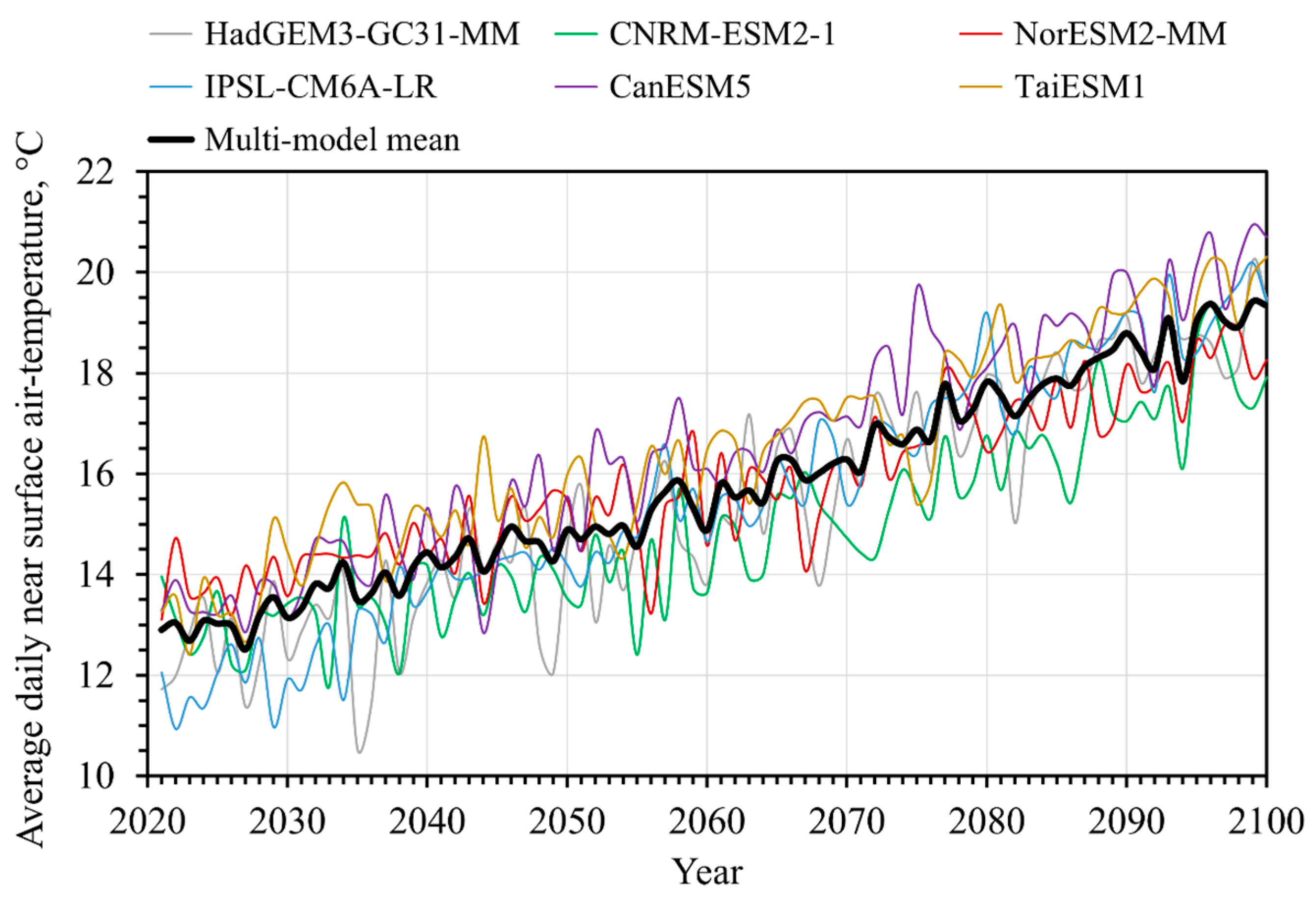
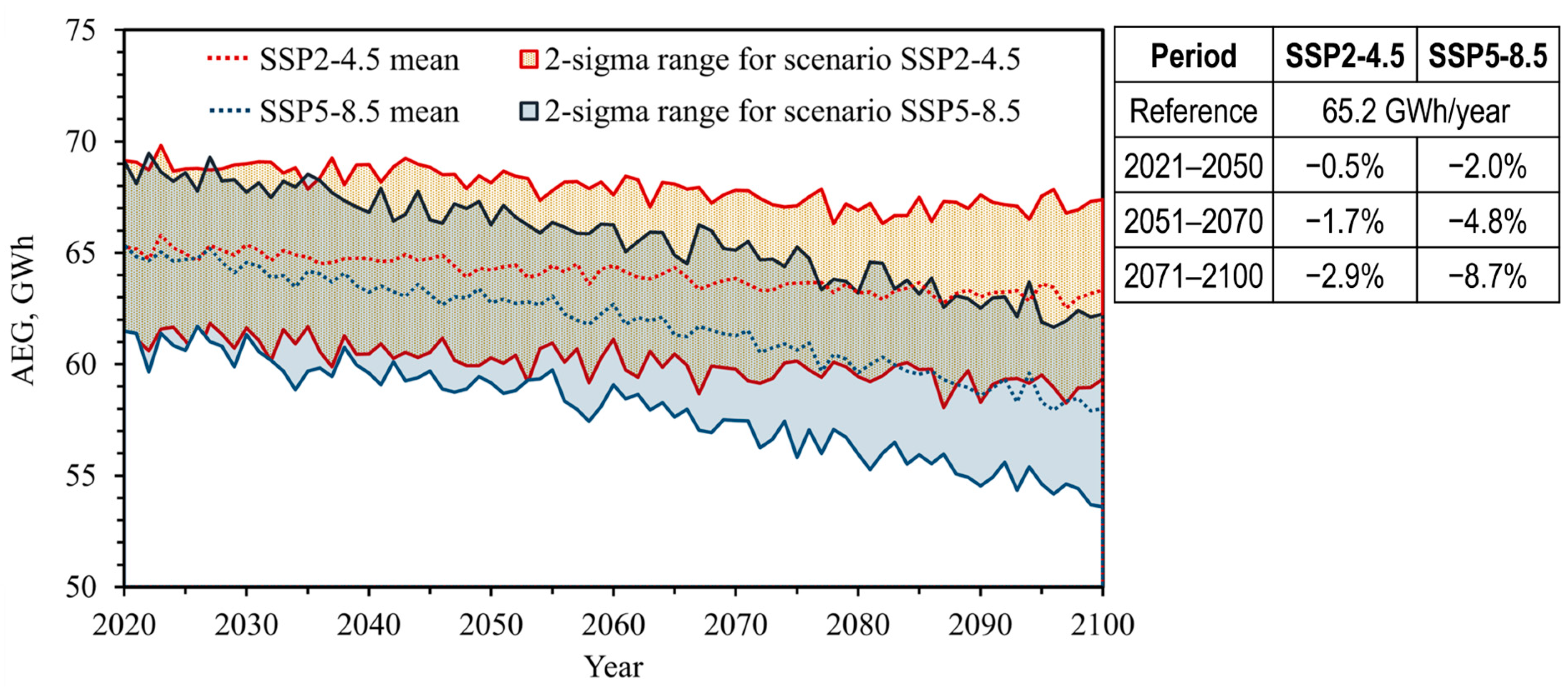
3.2. Future Thermoeconomic Performance of the Geothermal Power Plant
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sanyal, S.K.; Enedy, S.K. Fifty Years of Power Generation at the Geysers Geothermal Field, California—The Lessons Learned. In Proceeding of the 36th Workshop on Geothermal Reservoir Engineering, Stanford University, Stanford, CA, USA, 31 January–2 February 2011. [Google Scholar]
- EIA: Electricity Data Browser, Number of Geothermal Power Plants, USA. Available online: https://www.eia.gov/electricity/data/browser/#/topic/1?agg=2,0,1&fuel=001&geo=g&sec=g&freq=A&rtype=s&start=2001&end=2023&ctype=linechart<ype=pin&rse=0&pin=&maptype=0 (accessed on 1 June 2024).
- Fridriksson, T.; Merino, A.M.; Orucu, A.Y.; Audinet, P. Greenhouse Gas Emissions from Geothermal Power Production. In Proceedings of the 42nd Workshop on Geothermal Reservoir Engineering, Stanford University, Stanford, CA, USA, 13–15 February 2017. [Google Scholar]
- New Zealand Geothermal Association: Geothermal Emissions in New Zealand. Available online: https://www.nzgeothermal.org.nz/geothermal-in-nz/what-is-geothermal/ (accessed on 1 June 2024).
- IPCC. Special Report on Renewable Energy Sources and Climate Change Mitigation; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2011; Available online: https://www.ipcc.ch/site/assets/uploads/2018/03/SRREN_Full_Report-1.pdf (accessed on 1 June 2024).
- da Silva, B.C.; Virgílio, R.M.; Nogueira, L.A.H.; Silva, P.d.N.; Passos, F.O.; Welerson, C.C. Assessment of Climate Change Impact on Hydropower Generation: A Case Study for Três Marias Power Plant in Brazil. Climate 2023, 11, 201. [Google Scholar] [CrossRef]
- Dallison, R.J.H.; Patil, S.D. Impact of Climate Change on Hydropower Potential in the UK and Ireland. Renew. Energy 2023, 207, 611–628. [Google Scholar] [CrossRef]
- Kara, T.; Şahin, A.D. Implications of Climate Change on Wind Energy Potential. Sustainability 2023, 15, 14822. [Google Scholar] [CrossRef]
- Bonanno, R.; Viterbo, F.; Maurizio, R.G. Climate Change Impacts on Wind Power Generation for the Italian Peninsula. Reg. Environ. Chang. 2023, 23, 15. [Google Scholar] [CrossRef]
- Solaun, K.; Cerdá, E. Climate Change Impacts on Renewable Energy Generation. A Review of Quantitative Projections. Renew. Sustain. Energy Rev. 2019, 116, 109415. [Google Scholar] [CrossRef]
- van Vliet, M.T.H.; Wiberg, D.; Leduc, S.; Riahi, K. Power Generation System Vulnerability and Adaptation to Changes in Climate and Water Resources. Nat. Clim. Chang. 2016, 6, 375–380. [Google Scholar] [CrossRef]
- Georgopoulou, E.; Mirasgedis, S.; Sarafidis, Y.; Giannakopoulos, C.; Varotsos, K.V.; Gakis, N. Climate Change Impacts on the Energy System of a Climate-Vulnerable Mediterranean Country (Greece). Atmosphere 2024, 15, 286. [Google Scholar] [CrossRef]
- Congedo, P.M.; Baglivo, C.; D’Agostino, D.; Mazzeo, D. The Impact of Climate Change on Air Source Heat Pumps. Energy Convers. Manag. 2023, 276, 116554. [Google Scholar] [CrossRef]
- Mideksa, T.K.; Kallbekken, S. The Impact of Climate Change on the Electricity Market: A Review. Energy Policy 2010, 38, 3579–3585. [Google Scholar] [CrossRef]
- Osman, A.I.; Chen, L.; Yang, M.; Msigwa, G.; Farghali, M.; Fawzy, S.; Rooney, D.W.; Yap, P.S. Cost, Environmental Impact, and Resilience of Renewable Energy under a Changing Climate: A Review. Environ. Chem. Lett. 2022, 21, 741–764. [Google Scholar] [CrossRef]
- Girgibo, N.; Hiltunen, E.; Lü, X.; Mäkiranta, A.; Tuomi, V. Risks of Climate Change Effects on Renewable Energy Resources and the Effects of their Utilisation on the Environment. Energy Rep. 2024, 11, 1517–1534. [Google Scholar] [CrossRef]
- Linnerud, K.; Mideksa, T.K.; Eskeland, G.S. The Impact of Climate Change on Nuclear Power Supply. Energy J. 2011, 32, 149–168. [Google Scholar] [CrossRef]
- Petrakopoulou, F.; Robinson, A.; Olmeda-Delgado, M. Impact of Climate Change on Fossil Fuel Power-Plant Efficiency and Water Use. J. Clean. Prod. 2020, 273, 122816. [Google Scholar] [CrossRef]
- Canales, F.A.; Jadwiszczak, P.; Jurasz, J.; Wdowikowski, M.; Ciapała, B.; Kaźmierczak, B. The Impact of Long-term Changes in Air Temperature on Renewable Energy in Poland. Sci. Total Environ. 2020, 729, 138965. [Google Scholar] [CrossRef] [PubMed]
- Yu, F.W.; Chan, K.T.; Sit, R.K.Y.; Yang, J. Energy Simulation of Sustainable Air-cooled Chiller System for Commercial Buildings under Climate Change. Energy Build. 2013, 64, 162–171. [Google Scholar] [CrossRef]
- Ma-oon, K. Geothermal Power Plant Project Ijen Bondowoso: Climate Change Risk Assessment, MedcoEnergi Geothermal, Project 0694710, Bangkok, Thailand. 2023. Available online: https://www3.dfc.gov/environment/eia/ijen/Climate_Change_Risk_Assessment.pdf (accessed on 1 June 2024).
- Algieri, A. Energy Exploitation of High-Temperature Geothermal Sources in Volcanic Areas: A Possible ORC Application in Phlegraean Fields (Southern Italy). Energies 2018, 11, 618. [Google Scholar] [CrossRef]
- Vanslambrouck, B.; Vankeirsbilck, I.; van den Broek, M.; Gusev, S.; De Paepe, M. Efficiency Comparison between the Steam Cycle and the Organic Rankine Cycle for Small Scale Power Generation. In Proceedings of the Renewable Energy World Conference & Expo North America, Long Beach, CA, USA, 14–16 February 2012. [Google Scholar]
- EVAPCO: Eco-Air: Industrial Air-Cooled Condensers. 2020. Bulletin 1100B, 2M/3-19/DGD. Available online: https://www.evapco.com/sites/evapco.com/files/2019-04/eco-Air-Condensers-Brochure-1100B-4.2.2019-web.pdf (accessed on 1 June 2024).
- Wang, C.-C.; Chi, K.-Y. Heat Transfer and Friction Characteristics of Plain Fin-and-Tube Heat Exchangers, Part I: New Experimental Data. Int. J. Heat Mass Transf. 2000, 43, 2681–2691. [Google Scholar] [CrossRef]
- Wang, C.-C.; Chi, K.-Y.; Chang, C.-J. Heat Transfer and Friction Characteristics of Plain Fin-and-Tube Heat Exchangers, Part II: Correlation. Int. J. Heat Mass Transf. 2000, 43, 2693–2700. [Google Scholar] [CrossRef]
- Shah, R.K.; Sekulić, D.P. Fundamentals of Heat Exchanger Design; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2003. [Google Scholar]
- Dobson, M.K.; Chato, J.C. Condensation in Smooth Horizontal Tubes. ASME J. Heat Mass Transf. 1998, 120, 193–213. [Google Scholar] [CrossRef]
- Collier, J.G.; Thome, J.R. Convective Boiling and Condensation, 3rd ed.; Oxford Engineering Science Series: Oxford, UK, 1996. [Google Scholar]
- Yunus, A.C.; Afshin, J.G. Heat and Mass Transfer: Fundamentals and Applications, 6th ed.; McGraw-Hill Education: New York, NY, USA, 2020. [Google Scholar]
- Serth, R.W.; Lestina, T. Process Heat Transfer: Principles, Applications and Rules of Thumb, 2nd ed.; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Intergovernmental Panel for Climate Change (IPCC): Sixth Assessment Report (AR6). 2021. Available online: https://www.ipcc.ch/assessment-report/ar6/ (accessed on 1 June 2024).
- Copernicus Climate Change Service, Climate Data Store (CDS): CMIP6 Climate Projections. 2021. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/10.24381/cds.c866074c?tab=overview (accessed on 1 June 2024).
- Croatian Meteorological and Hydrological Service (DHMZ): Climate—Daily Mean Temperature. Available online: https://meteo.hr/klima_e.php?section=klima_pracenje¶m=srednja_temperatura (accessed on 1 June 2024).
- Weiss, A.; Hays, C.J. Calculating Daily Mean Air Temperatures by Different Methods: Implications from a Non-Linear Algorithm. Agric. For. Meteorol. 2005, 128, 57–65. [Google Scholar] [CrossRef]
- Climate Change Knowledge Portal: Climate Projections—Mean Projections, Country: Croatia. Available online: https://climateknowledgeportal.worldbank.org/country/croatia/climate-data-projections (accessed on 1 June 2024).

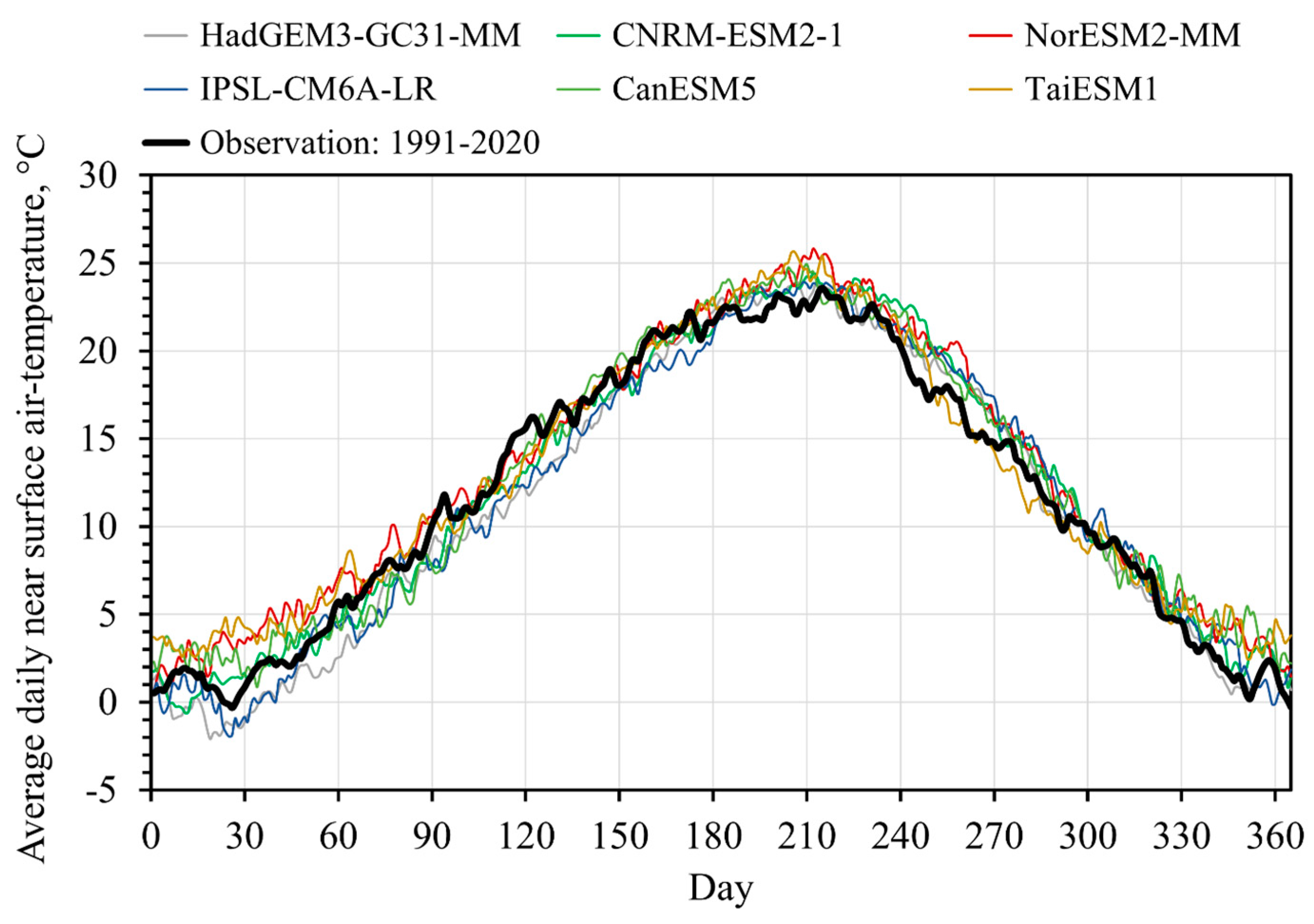


| Climate Model | RMSE, °C | KL, - | RMSE Rank | KL Rank | Average Rank Score | Overall Rank |
|---|---|---|---|---|---|---|
| HadGEM3-GC31-MM | 1.529 | 0.256 | 2 | 3 | 2.5 | 1 |
| CNRM-ESM2-1 | 1.377 | 0.283 | 1 | 5 | 3.0 | 2 |
| NorESM2-MM | 1.627 | 0.280 | 5 | 4 | 4.5 | 3 |
| IPSL-CM6A-LR | 1.566 | 0.351 | 4 | 9 | 6.5 | 4 |
| CanESM5 | 1.551 | 0.444 | 3 | 13 | 8.0 | 5 |
| TaiESM1 | 1.629 | 0.371 | 6 | 10 | 8.0 | 5 |
| CESM2-WACCM | 1.894 | 0.256 | 15 | 2 | 8.5 | 7 |
| HadGEM3-GC31-LL | 2.243 | 0.249 | 16 | 1 | 8.5 | 7 |
| CNRM-CM6-1 | 1.683 | 0.323 | 11 | 7 | 9.0 | 9 |
| CNRM-CM6-1-HR | 1.647 | 0.421 | 9 | 11 | 10.0 | 10 |
| CMCC-ESM2 | 1.643 | 0.446 | 7 | 15 | 11.0 | 11 |
| MRI-ESM2-0 | 1.858 | 0.344 | 14 | 8 | 11.0 | 11 |
| MIROC6 | 1.664 | 0.487 | 10 | 17 | 13.5 | 13 |
| EC-Earth3-CC | 1.645 | 0.544 | 8 | 19 | 13.5 | 13 |
| CMCC-CM2-SR5 | 2.319 | 0.439 | 17 | 12 | 14.5 | 15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blecich, P.; Wolf, I.; Senčić, T.; Bonefačić, I. Impact of Climate Change on the Thermoeconomic Performance of Binary-Cycle Geothermal Power Plants. Eng. Proc. 2024, 67, 29. https://doi.org/10.3390/engproc2024067029
Blecich P, Wolf I, Senčić T, Bonefačić I. Impact of Climate Change on the Thermoeconomic Performance of Binary-Cycle Geothermal Power Plants. Engineering Proceedings. 2024; 67(1):29. https://doi.org/10.3390/engproc2024067029
Chicago/Turabian StyleBlecich, Paolo, Igor Wolf, Tomislav Senčić, and Igor Bonefačić. 2024. "Impact of Climate Change on the Thermoeconomic Performance of Binary-Cycle Geothermal Power Plants" Engineering Proceedings 67, no. 1: 29. https://doi.org/10.3390/engproc2024067029
APA StyleBlecich, P., Wolf, I., Senčić, T., & Bonefačić, I. (2024). Impact of Climate Change on the Thermoeconomic Performance of Binary-Cycle Geothermal Power Plants. Engineering Proceedings, 67(1), 29. https://doi.org/10.3390/engproc2024067029








