Abstract
Singular spectrum analysis allows automation for the extraction of trends of arbitrary shapes. Here, we study how the estimation of signal ranks influences the accuracy of trend extraction and forecasting. It is numerically shown that the trend estimates and their forecasting are slightly changed if the signal rank is overestimated. If the trend is not of finite rank, the trend estimates are still stable, while forecasting may be unstable. The method of automation of the trend extraction includes an important step for improving the separability of time series components to avoid their mixture. However, the better the separability improvement, the larger the forecasting variability, since the noise components become separated and can be similar to trend ones.
1. Introduction
Consider the problem of trend extraction and forecasting using singular spectrum analysis (SSA) [1,2,3,4,5]. The method of singular spectrum analysis (SSA) is a well-established approach for trend extraction and forecasting. Many research papers have applied SSA to real-life time series data, demonstrating its usefulness (see, for example, the review paper [6]). One of the advantages of SSA is that it does not require a time series model to decompose it into interpretable components such as trends, periodicities, and noise. However, this can make it challenging to automatically identify these components.
An outline of SSA for a time series of length N is shown below, with the window length L and component grouping method being the main parameters.
Let be the observed time series of length N and , where is the structured part of the time series (the signal) and is noise, i.e., fast irregular oscillations around zero; we will consider white Gaussian noise. In its turn, let , where is the trend, i.e., the slowly varying component of the series, and is the periodic component (optionally). Suppose we are interested in , and assume the approximate separability of the time series and (see [4], Sections 1.5 and 6.1, for the definition of separability).
The Basic SSA schema for component extraction is as follows:
Here, is the projector by the Frobenius norm on the set of Hankel matrices.
For signal extraction, we take the group of the leading components , where the value of p, if the noise is not too large, should be equal to the signal rank r. By the L-rank r of a signal , we mean the rank of its trajectory matrix . Singular vectors of the trajectory matrix ( and ), as well as elementary reconstructed series obtained based on elementary grouping (each group consists of one component of the decomposition), have the property that if a signal component is separated from the residual in the decomposition, the above elements generated by it have the same structure as the signal component itself. For example, a trend produces slowly varying components, while a harmonic produces harmonic components of the same frequency. A problem can arise when the component is poorly separable; however, special methods exist and are being developed to improve it (known as nested oblique singular spectrum analysis, OSSA; see the review in [7]). This idea forms the basis for intelligent automatic identification.
Most algorithms for automatic identification [8,9,10,11] only work well under conditions of good trend separability. In [7], we proposed an approach that combines methods for improving separability with automatic trend identification. To use this approach, the algorithm should be applied to the group of p leading components, where p is ideally equal to the rank r of the signal for finite-rank signals.
As SSA can be applied to signals that are not of finite rank, there are no accurate methods available for estimating the number of components for signal extraction using the SSA method. Therefore, it is important to understand how automatic trend detection methods described in [7] work when rank estimation is inaccurate. In [7], it has been shown, through several examples, that the error in trend extraction increases slightly when the rank estimation is exceeded slightly. In this paper, we will conduct a more comprehensive study and also evaluate the accuracy of the prediction.
2. Basic Notions
- Signal ranks
Let us introduce several definitions. By time series of length N, we mean a sequence of real numbers . Consider a time series in the form of the sum of a signal and noise, , and state the problem of signal estimation and forecasting.
A signal has rank (and is called a series of finite rank, or low rank) if its L-rank equals r for any L, such that . Recall that the L-rank equals the rank of the trajectory matrix.
- LRR and forecasting
A series of finite rank satisfies linear recurrence relations (LRRs) of order d, , under some mild restrictions [4]:
where the order of the minimal LRR equals r. Recurrent SSA forecasting is performed by a specific LRR [4,5].
For prediction in SSA, it is assumed that the signal satisfies a linear recurrence relation (maybe, approximately). According to [12], an infinite time series satisfies the LRR if and only if for some q and . This assumption is valid for real signals in the form of a sum of products of polynomial, exponential, and sinusoidal time series. SSA also works for the case of trend extraction and the general case of amplitude-modulated harmonics, where the model is satisfied approximately. Since the set of signals of finite rank is wide, trends are typically well-approximated.
- Examples of finite-rank time signals
Consider a time series .
Example 1.
Let , . Rank is equal to 1 if and 2 if .
Example 2.
For exponential time series with , the rank is equal to 1. For polynomial signals of order m, the rank equals .
- Choice of window length
If the signal is of finite rank, it is recommended to choose the window length near the half of time series length. If the structure of the time series is complex and probably slowly changing, it is better to choose the window length smaller.
Automation of Trend Identification
In the Introduction, we described the SSA algorithm in a general form. In Figure 1, an extended version of the flowchart of automatic trend extraction taken from [7] is presented. In particular, we add a step for the choice of the number p of signal components and accent the numbers of components at each step.
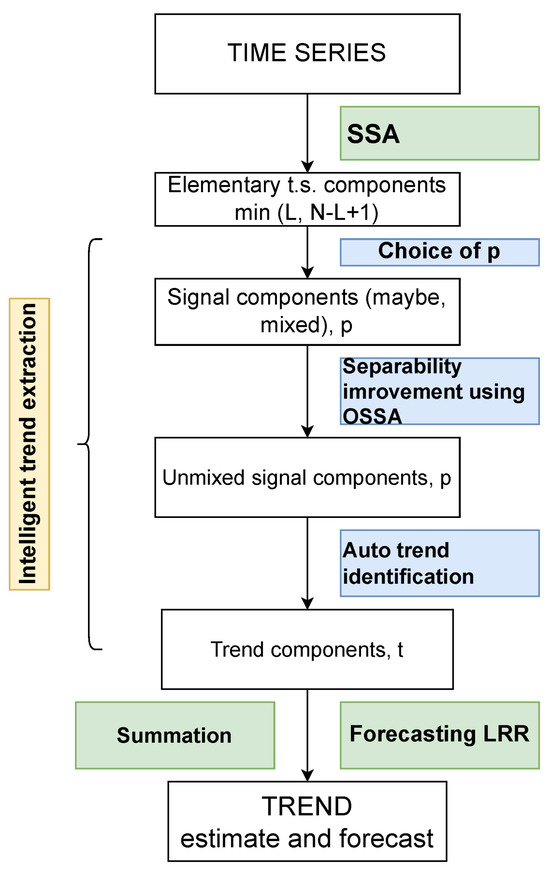
Figure 1.
Flowchart of intelligent trend extraction and prediction.
Below, we refer to rank estimates as p, for short. However, it is just the number of components considered for trend identification. For the case of low-rank signals and an appropriate level of noise, the choice of p equal to the signal rank is the best. If a part of the signal is mixed with noise, or if the signal is just approximated by different time series of different ranks, then the choice of p is not a well-posed problem. The paper aims to numerically study the dependence of reconstruction and forecasting accuracy on the choice of p. It is clear that if the number of a trend elementary components is larger than p, the accuracy will be bad. Therefore, the question is about the influence of overestimating p on the accuracy. Note that overestimating p means that the trend identification algorithm is applied to noise components, among others.
We will consider the trend reconstruction and forecasting following the scheme depicted in Figure 1. The study in Section 3 will be performed for AutoSSA, where the step of separability improvement is omitted, and for AutoEOSSA, where the separability improvement is performed by EOSSA [7] with the recommended parameters.
The automation of trend identification has two parameters, the upper bound , , for frequencies that we refer to the trend and the threshold T, , for the contribution of the trend range of frequencies. The recommended parameters are and ; the last is for the added seasonality with fundamental frequency 1/12.
3. Dependence on Rank Estimation
Let us describe the numerical experiments. In the case of artificial time series, where the trend and its exact prediction are known, we will consider the RMSE for the deviation from the signal based on 100 simulated time series. We fix the signal, the noise level and the range of ranks. For each rank value, we estimate the signal and perform the recurrent SSA forecasting.
In real-life time series, we cannot determine the true trend and its forecast; therefore, we can only estimate the error on the evaluation segments of the time series.
3.1. Numerical Experiments
For the signals where the trends are well separated from the seasonality using SSA, AutoSSA works similarly to the methods with separability improvement and even more stable concerning rank overestimation. Here, we present an artificial example when the trend is mixed with the seasonality.
Let and . Consider the forecasting with a horizon of 40. The signal takes the form
the noise is white Gaussian with zero mean and unit variance.
Figure 2 illustrates the inaccurate forecasting performance of AutoSSA for any selected r, owing to the presence of a mixed trend and seasonality component in the sample time series.
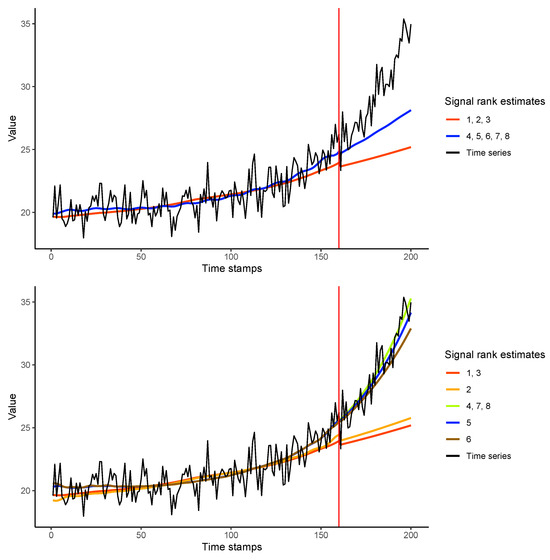
Figure 2.
Example (2): RMSE: AutoSSA (top) and AutoEOSSA (bottom).
The signal has rank 4. It can be observed in Table 1 that minimal average errors are achieved for rank estimates larger than or equal to 4 (the number of realizations was 100). However, AutoSSA fails to accurately extract the trend due to possible mixing, whereas AutoEOSSA can effectively extract and predict the trend with precision.

Table 1.
Example (2): RMSE. ‘_rec’ means reconstruction errors, ‘_for’ means forecasting errors.
3.2. Real-Life Examples
In this section, we demonstrate the dependence of trend prediction accuracy on the number of components, referred to the signal, using a real-life dataset. Let us consider the widely studied dataset of Australian wine sales and take the ‘Red wine’ series of length 176 (monthly red wine sales, Australia, from January 1980 to August 1994, thousands of litres); see Figure 3. We cut the last 48 points, and apply SSA to the first 128 points (to August 1992), with the window length equal to 36. We choose a window length smaller than half of the time series length; the latter is recommended for the case of finite-rank time series; however, it seems the behaviour of the time series is changed in 1992. The choice of a large window length would ignore this change.
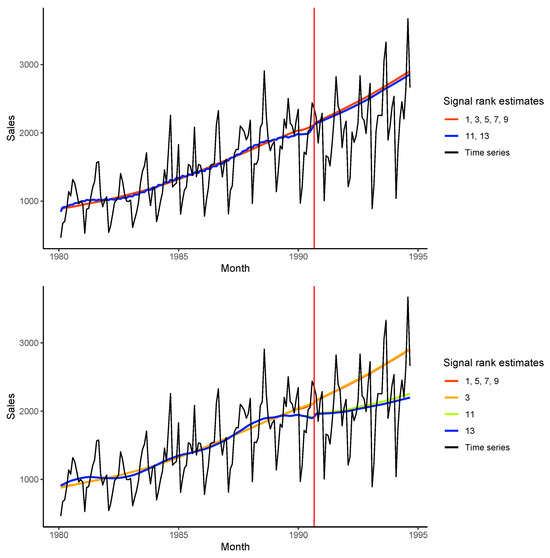
Figure 3.
Example ‘Red wine’: AutoSSA (top) and AutoEOSSA (bottom).
Figure 3 illustrates that there are two potential future scenarios. The behaviour observed before 1992 does not necessarily determine future trends. This may explain why trend reconstructions obtained from different estimates of rank r yield distinct forecasts. The AutoEOSSA algorithm with improved separability can extract trend components from the components mixed with noise, whereas AutoSSA is not able to do this. Both methods select one component for reconstruction for estimated ranks less than 11 and two components for ranks 11, 12, 13 (we did not consider larger ranks). However, the second component in AutoSSA is only a small part of the trend due to mixing with seasonality. Note that for AutoSSA, the trend reconstructions and forecasts are the same for the same identified trend components. For AutoEOSSA, they may vary slightly due to different results of the separability improvement.
External information can help to select the appropriate scenario. In addition, a validation period can be used to identify the optimal rank estimation. The scenario with the smaller prediction errors over the validation period is recommended for prediction. We divide the last 48 points into two equal segments: the first 24 points for validation and the last 24 points as test data.
For comparison, Figure 4 contains the forecasts provided by polynomial regressions. One can see that the results are unstable. The best accuracy corresponds to linear and cubic regressions. Table 2 contains the forecasting errors (RMSE) for best scenarios in SSA and polynomial regression forecasting. Linear regression confirms its stability. In the case when the time series has a linear tendency, it may be the best approach. The attempt to describe the time series behaviour in more detail by polynomial regression is not a good choice for forecasting due to its random variability.
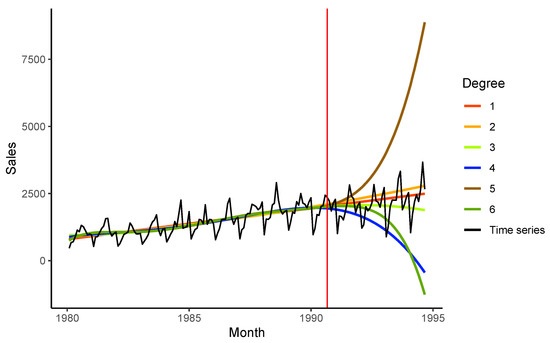
Figure 4.
Example ‘Red wine’: Polynomial regression.

Table 2.
‘Red wine’: RMSE on validation and test periods.
4. Conclusions
Thus, we demonstrated how the extraction of SSA trends and their forecasting are impacted by the estimated number of signal components. The stability with respect to rank estimation is crucial for real-life applications, as real-life trends are typically not of finite rank, rendering the problem of rank estimation ill-posed. We refer to the number of components that yield the lowest errors as the optimal number of components.
For artificial examples, the errors of trend reconstruction and forecasting can be calculated. Numerical experiments demonstrate the stability of trend reconstruction and forecasting for these examples.
For real-life time series, we can only measure the errors of forecasting the whole time series. To mitigate the variability of forecasting, we suggest trying many different numbers of components for trend identification and choosing the one that gives the smallest errors over the validation period. This method works for trends with different shapes, but it may not work as well for all time series, since it depends on how well the trend stays the same in the future.
Furthermore, the choice of method for improving separability may have a minor impact on trend extraction, but a significant impact on forecasting. This creates a trade-off between forecasting bias and variability. Without separability improvement, the forecast remains stable; however, if mixed trend components are undetected, the forecast becomes biased. By using a method for separability improvement, slowly varying parts of the noise components can be extracted, resulting in forecasting variability. If forecasting is performed for a group of similar time series, the decision between bias and variability can be made by analysing several sample time series.
Author Contributions
Conceptualization, N.G.; methodology, N.G. and P.D.; software, P.D.; validation, N.G. and P.D.; formal analysis, N.G. and P.D.; investigation, N.G. and P.D.; resources, N.G.; data curation, N.G. and P.D.; writing—original draft preparation, N.G. and P.D.; writing—review and editing, N.G. and P.D.; visualization, N.G. and P.D.; supervision, N.G.; project administration, N.G.; funding acquisition, N.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Russian Science Foundation (project No. 23-21-00222).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are openly available. The R-code for data generation and result replication can be found at https://zenodo.org/records/12601554, doi https://doi.org/10.5281/zenodo.12601554.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Broomhead, D.; King, G. Extracting qualitative dynamics from experimental data. Phys. D Nonlinear Phenom. 1986, 20, 217–236. [Google Scholar] [CrossRef]
- Vautard, R.; Ghil, M. Singular spectrum analysis in nonlinear dynamics, with applications to paleoclimatic time series. Phys. D Nonlinear Phenom. 1989, 35, 395–424. [Google Scholar] [CrossRef]
- Elsner, J.B.; Tsonis, A.A. Singular Spectrum Analysis: A New Tool in Time Series Analysis; Plenum Press: New York, NY, USA, 1996. [Google Scholar]
- Golyandina, N.; Nekrutkin, V.; Zhigljavsky, A. Analysis of Time Series Structure: SSA and Related Techniques; Chapman & Hall/CRC: Boca Raton, FL, USA, 2001. [Google Scholar]
- Golyandina, N.; Zhigljavsky, A. Singular Spectrum Analysis for Time Series, 2nd ed.; Springer Briefs in Statistics; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Golyandina, N. Particularities and commonalities of singular spectrum analysis as a method of time series analysis and signal processing. Wiley Interdiscip. Rev. Comput. Stat. 2020, 12, e1487. [Google Scholar] [CrossRef]
- Golyandina, N.; Dudnik, P.; Shlemov, A. Intelligent Identification of Trend Components in Singular Spectrum Analysis. Algorithms 2023, 16, 353. [Google Scholar] [CrossRef]
- Vautard, R.; Yiou, P.; Ghil, M. Singular-Spectrum Analysis: A toolkit for short, noisy chaotic signals. Phys. D 1992, 58, 95–126. [Google Scholar] [CrossRef]
- Alexandrov, T. A method of trend extraction using Singular Spectrum Analysis. RevStat 2009, 7, 1–22. [Google Scholar]
- Romero, F.; Alonso, F.; Cubero, J.; Galán-Marín, G. An automatic SSA-based de-noising and smoothing technique for surface electromyography signals. Biomed. Signal Process. Control 2015, 18, 317–324. [Google Scholar] [CrossRef]
- Kalantari, M.; Hassani, H. Automatic Grouping in Singular Spectrum Analysis. Forecasting 2019, 1, 189–204. [Google Scholar] [CrossRef]
- Hall, M.J. Combinatorial Theory; Wiley: New York, NY, USA, 1998. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).