JET: Fast Estimation of Hierarchical Time Series Clustering †
Abstract
:1. Introduction
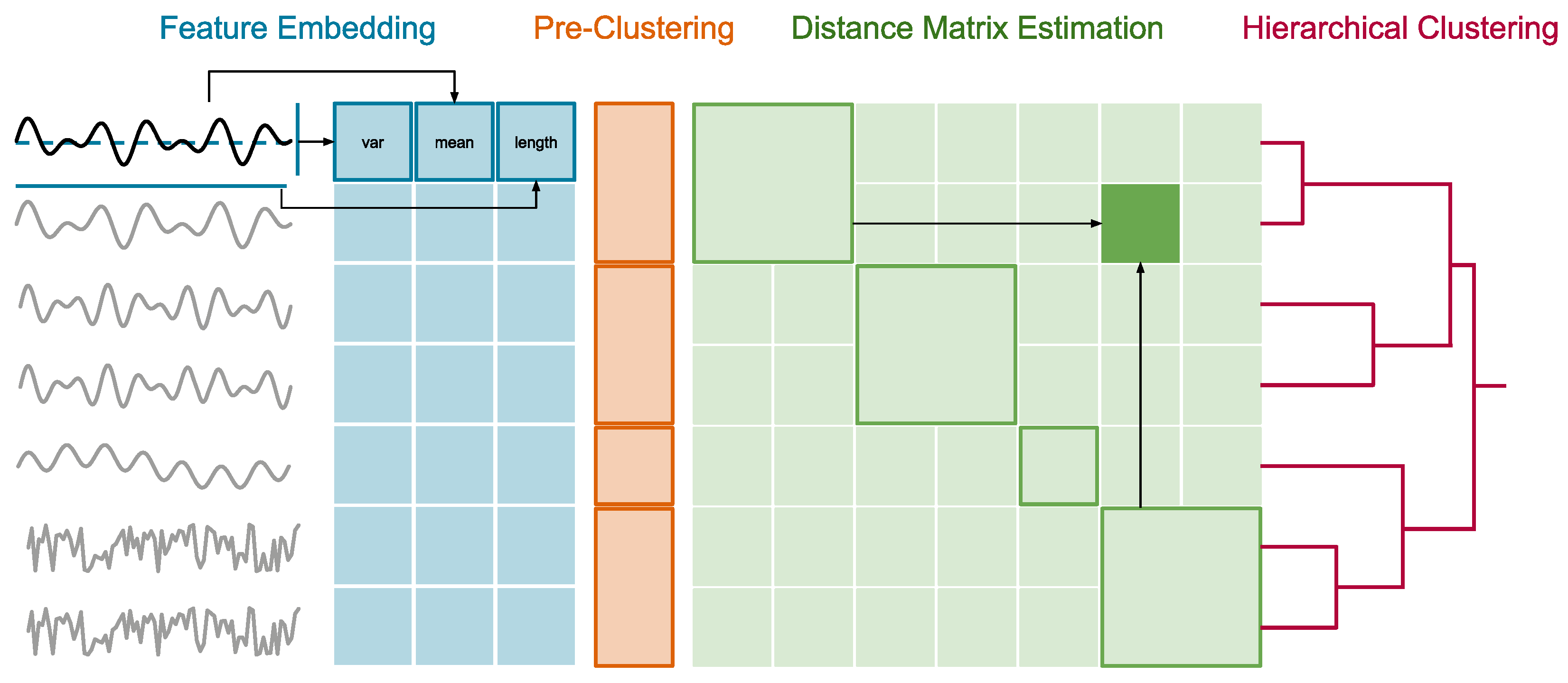
- Time Series Clustering via JET: We propose the approximate HC algorithm JET, which (1) embeds arbitrary long time series into a fixed-sized space by extracting representative time series features, (2) runs fast but coarse-grained pre-clustering with a pessimistically high number of groups, (3) approximates group-to-group time series distances with the centroid distances of the groups, and (4) calculates full hierarchical clustering with the partially approximated, but still highly accurate, distances (Section 4).
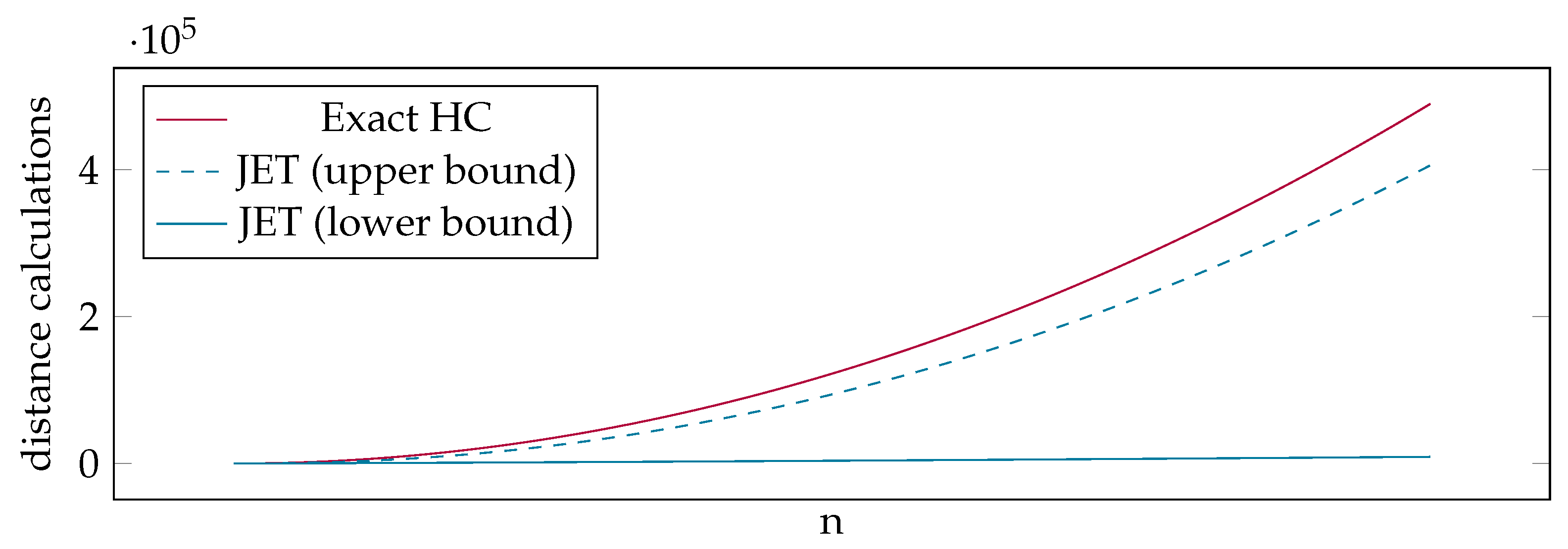
- Theoretical Runtime Analysis of JET: We provide a theoretical analysis of our distance matrix estimation by calculating the best and worst case runtimes. Our analysis shows that even in the worst case, JET is significantly faster than an exact calculation of the entire distance matrix (Section 5).
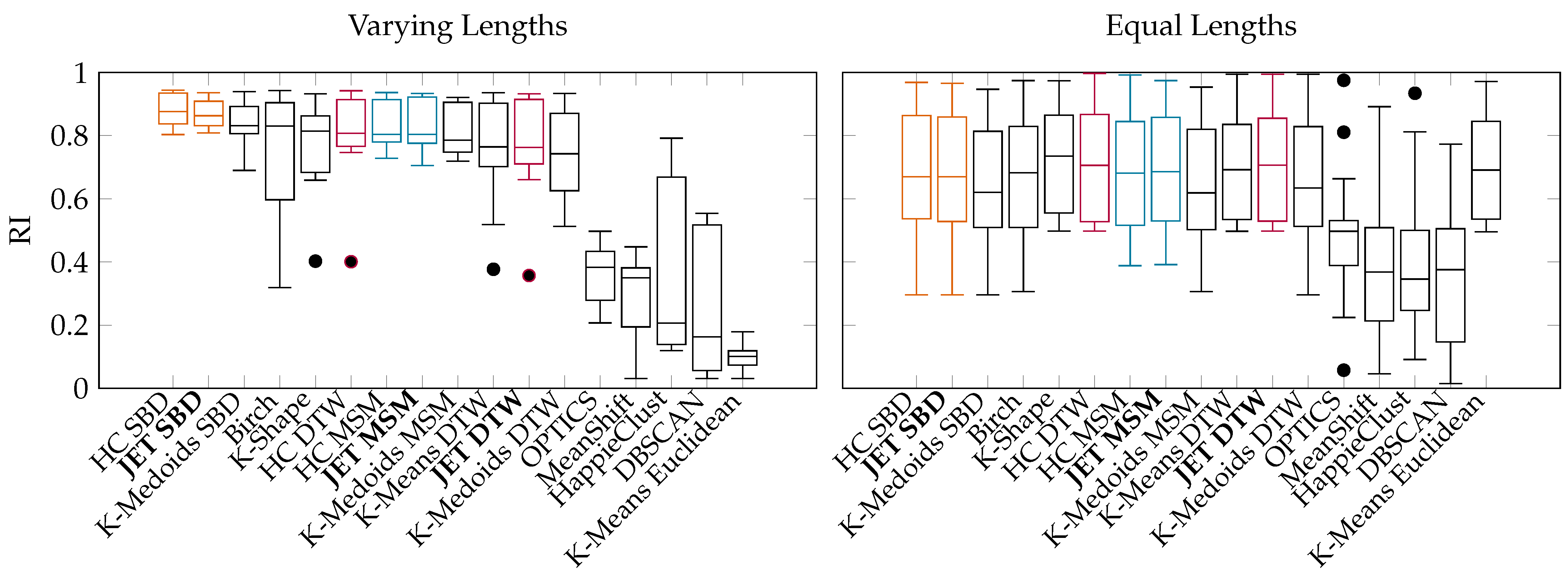
- Performance and Quality Evaluation of JET: We demonstrate the applicability of popular algorithms to time series clustering and report on the quality and runtime on well-known datasets. The evaluation shows that JET outperforms similarly accurate state-of-the-art approaches in runtime and similarly efficient approaches in accuracy (Section 6).
2. Advancing Jet Engine Development
3. Related Work
3.1. Clustering Approaches
3.2. Distance Measures
4. Jaunty Estimation of Hierarchical Time Series Clustering
| Algorithm 1: JET | |
| 1: procedure JET() 2: | |
| 3: | ▹ Section 4.1 |
| 4: for do 5: for do 6: | |
| 7: | ▹ Section 4.2 |
| 8: | ▹ Section 4.3 |
| 9: 10: | |
| 11: for do | ▹ Centroid Distance Matrix |
| 12: 13: for do 14: 15: 16: | |
| 17: for do | ▹ Full Distance Matrix |
| 18: 19: for do 20: 21: if then 22: 23: 24: else 25: 26: | |
| 27: | ▹ Section 4.4 |
| 28: return |
4.1. Feature Embedding
4.2. Pre-Clustering
4.3. Distance Matrix Estimation
4.4. Hierarchical Clustering
5. Theoretical Runtime Analysis
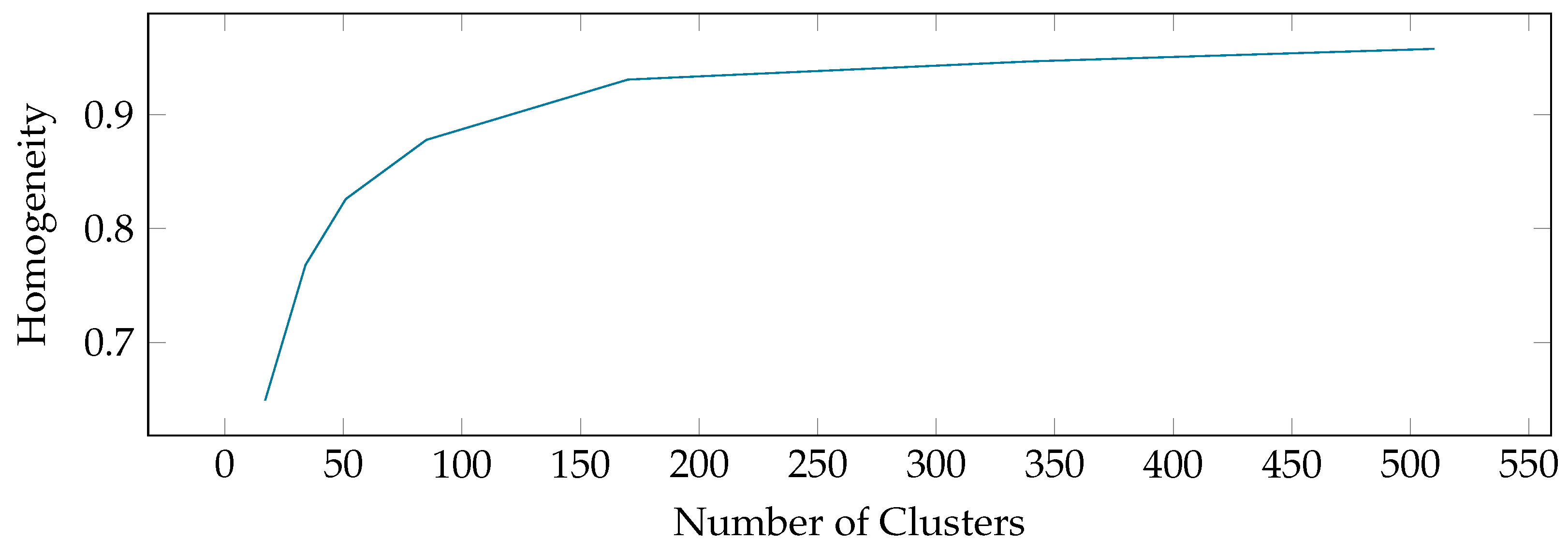
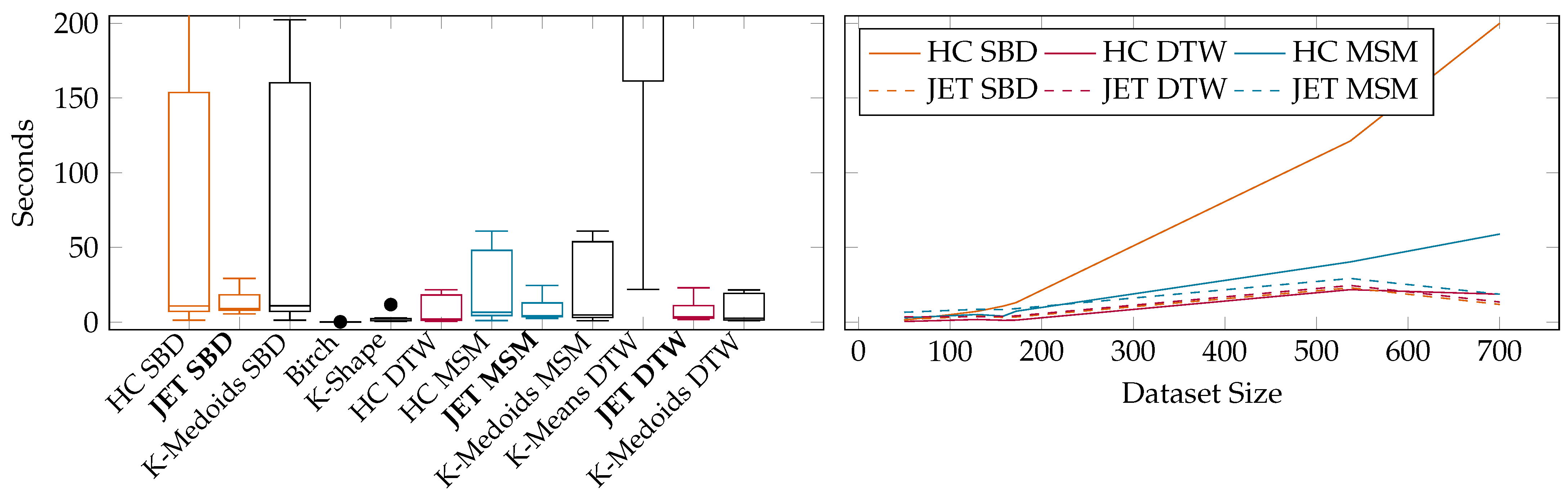
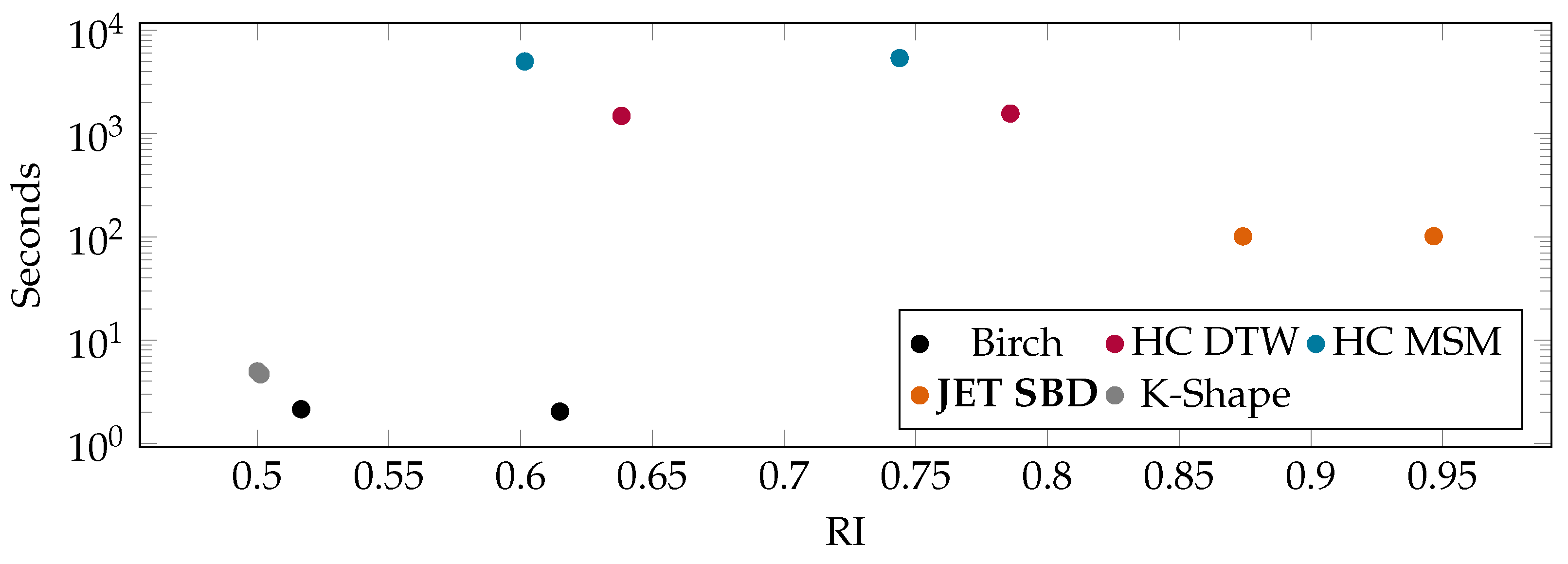
6. Experimental Evaluation
6.1. Experimental Setup
6.2. Benchmarks on Publicly Available UCR Data
6.3. Benchmarks on Rolls-Royce Industry Data
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ansari, S.; Farzaneh, N.; Duda, M.; Horan, K.; Andersson, H.B.; Goldberger, Z.D.; Nallamothu, B.K.; Najarian, K. A Review of Automated Methods for Detection of Myocardial Ischemia and Infarction Using Electrocardiogram and Electronic Health Records. IEEE Rev. Biomed. Eng. 2017, 10, 264–298. [Google Scholar] [CrossRef] [PubMed]
- Woike, M.; Abdul-Aziz, A.; Clem, M. Structural health monitoring on turbine engines using microwave blade tip clearance sensors. In Proceedings of the Smart Sensor Phenomena, Technology, Networks, and Systems Integration 2014, San Diego, CA, USA, 10–11 March 2014; Volume 9062, pp. 167–180. [Google Scholar] [CrossRef]
- Cheng, H.; Tan, P.N.; Potter, C.; Klooster, S. Detection and Characterization of Anomalies in Multivariate Time Series. In Proceedings of the SIAM International Conference on Data Mining (SDM), Sparks, NV, USA, 30 April–2 May 2009; pp. 413–424. [Google Scholar] [CrossRef]
- Braei, M.; Wagner, S. Anomaly Detection in Univariate Time-series: A Survey on the State-of-the-Art. arXiv 2020, arXiv:2004.00433. [Google Scholar]
- Blázquez-García, A.; Conde, A.; Mori, U.; Lozano, J.A. A Review on Outlier/Anomaly Detection in Time Series Data. arXiv 2020, arXiv:2002.04236. [Google Scholar] [CrossRef]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly Detection: A Survey. ACM Comput. Surv. 2009, 41, 1–58. [Google Scholar] [CrossRef]
- Schmidl, S.; Wenig, P.; Papenbrock, T. Anomaly Detection in Time Series: A Comprehensive Evaluation. In Proceedings of the VLDB Endowment, Sydney, Australia, 5–9 September 2022. [Google Scholar]
- Malhotra, P.; Vig, L.; Shroff, G.; Agarwal, P. Long short term memory networks for anomaly detection in time series. In Proceedings of the European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning (ESANN), Bruges, Belgium, 22–23 April 2015. [Google Scholar]
- Ryzhikov, A.; Borisyak, M.; Ustyuzhanin, A.; Derkach, D. Normalizing flows for deep anomaly detection. arXiv 2019, arXiv:1912.09323. [Google Scholar]
- Boniol, P.; Palpanas, T. Series2Graph: Graph-Based Subsequence Anomaly Detection for Time Series. Proc. VLDB Endow. 2020, 13, 1821–1834. [Google Scholar] [CrossRef]
- Zhu, Y.; Zimmerman, Z.; Senobari, N.S.; Yeh, C.C.M.; Funning, G.; Mueen, A.; Brisk, P.; Keogh, E. Matrix Profile II: Exploiting a Novel Algorithm and GPUs to Break the One Hundred Million Barrier for Time Series Motifs and Joins. In Proceedings of the International Conference on Data Mining (ICDM), Barcelona, Spain, 12–15 December 2016; pp. 739–748. [Google Scholar] [CrossRef]
- Bianco, A.M.; Ben, M.G.; Martínez, E.J.; Yohai, V.J. Outlier Detection in Regression Models with ARIMA Errors Using Robust Estimates. J. Forecast. 2001, 20, 565–579. [Google Scholar] [CrossRef]
- Hochenbaum, J.; Vallis, O.S.; Kejariwal, A. Automatic Anomaly Detection in the Cloud Via Statistical Learning. arXiv 2017, arXiv:1704.07706. [Google Scholar]
- MacQueen, J. Some Methods for Classification and Analysis of Multivariate Observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 21 June–18 July 1965 and 27 December 1965–7 January 1966; University of California Press: Berkeley, CA, USA, 1967. [Google Scholar]
- Kaufman, L.; Rousseeuw, P.J. Partitioning around medoids (program pam). Find. Groups Data Introd. Clust. Anal. 1990, 344, 68–125. [Google Scholar]
- Cheng, Y. Mean shift, mode seeking, and clustering. IEEE Trans. Pattern Anal. Mach. Intell. 1995, 17, 790–799. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996. [Google Scholar]
- Ankerst, M.; Breunig, M.M.; Kriegel, H.P.; Sander, J. OPTICS: Ordering points to identify the clustering structure. ACM Sigmod Record 1999, 28, 49–60. [Google Scholar] [CrossRef]
- Petitjean, F.; Ketterlin, A.; Gançarski, P. A global averaging method for dynamic time warping, with applications to clustering. Pattern Recognit. 2011, 44, 678–693. [Google Scholar] [CrossRef]
- Berndt, D.J.; Clifford, J. Using dynamic time warping to find patterns in time series. In Proceedings of the KDD Workshop, Seattle, WA, USA, 31 July–1 August 1994; Volume 10, pp. 359–370. [Google Scholar]
- Paparrizos, J.; Gravano, L. k-shape: Efficient and accurate clustering of time series. In Proceedings of the 2015 ACM SIGMOD International Conference on Management of Data, Melbourne, VIC, Australia, 31 May–4 June 2015; pp. 1855–1870. [Google Scholar]
- Zhang, T.; Ramakrishnan, R.; Livny, M. BIRCH: A new data clustering algorithm and its applications. Data Min. Knowl. Discov. 1997, 1, 141–182. [Google Scholar] [CrossRef]
- Bonifati, A.; Buono, F.D.; Guerra, F.; Tiano, D. Time2Feat: Learning interpretable representations for multivariate time series clustering. Proc. VLDB Endow. 2022, 16, 193–201. [Google Scholar] [CrossRef]
- Nielsen, F. Hierarchical clustering. In Introduction to HPC with MPI for Data Science; Springer: Cham, Switzerland, 2016; pp. 195–211. [Google Scholar] [CrossRef]
- Ward, J.H., Jr. Hierarchical grouping to optimize an objective function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Gower, J.C.; Legendre, P. Metric and Euclidean properties of dissimilarity coefficients. J. Classif. 1986, 3, 5–48. [Google Scholar] [CrossRef]
- Kull, M.; Vilo, J. Fast approximate hierarchical clustering using similarity heuristics. BioData Min. 2008, 1, 1–14. [Google Scholar] [CrossRef]
- Monath, N.; Kobren, A.; Krishnamurthy, A.; Glass, M.R.; McCallum, A. Scalable Hierarchical Clustering with Tree Grafting. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ’19, New York, NY, USA, 4–8 August 2019; pp. 1438–1448. [Google Scholar] [CrossRef]
- Stefan, A.; Athitsos, V.; Das, G. The move-split-merge metric for time series. IEEE Trans. Knowl. Data Eng. 2012, 25, 1425–1438. [Google Scholar] [CrossRef]
- Holznigenkemper, J.; Komusiewicz, C.; Seeger, B. On computing exact means of time series using the move-split-merge metric. Data Min. Knowl. Discov. 2023, 37, 595–626. [Google Scholar] [CrossRef]
- Paparrizos, J.; Franklin, M.J. Grail: Efficient time-series representation learning. Proc. VLDB Endow. 2019, 12, 1762–1777. [Google Scholar] [CrossRef]
- Blue Yonder GmbH. tsfresh. 2023. Available online: https://github.com/blue-yonder/tsfresh (accessed on 3 July 2024).
- Rosenberg, A.; Hirschberg, J. V-measure: A conditional entropy-based external cluster evaluation measure. In Proceedings of the 2007 Joint Conference on Empirical Methods in Natural Language Processing and Computational Natural Language Learning (EMNLP-CoNLL), Prague, Czech Republic, 28–30 June 2007; pp. 410–420. [Google Scholar]
- Hubert, L.; Arabie, P. Comparing partitions. J. Classif. 1985, 2, 193–218. [Google Scholar] [CrossRef]
- Dau, H.A.; Keogh, E.; Kamgar, K.; Yeh, C.C.M.; Zhu, Y.; Gharghabi, S.; Ratanamahatana, C.A.; Yanping; Hu, B.; Begum, N.; et al. The UCR Time Series Classification Archive. 2018. Available online: https://www.cs.ucr.edu/~eamonn/time_series_data_2018/ (accessed on 3 July 2024).
- Tavenard, R.; Faouzi, J.; Vandewiele, G.; Divo, F.; Androz, G.; Holtz, C.; Payne, M.; Yurchak, R.; Rußwurm, M.; Kolar, K.; et al. Tslearn, A Machine Learning Toolkit for Time Series Data. J. Mach. Learn. Res. 2020, 21, 1–6. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wenig, P.; Höfgen, M.; Papenbrock, T. JET: Fast Estimation of Hierarchical Time Series Clustering. Eng. Proc. 2024, 68, 37. https://doi.org/10.3390/engproc2024068037
Wenig P, Höfgen M, Papenbrock T. JET: Fast Estimation of Hierarchical Time Series Clustering. Engineering Proceedings. 2024; 68(1):37. https://doi.org/10.3390/engproc2024068037
Chicago/Turabian StyleWenig, Phillip, Mathias Höfgen, and Thorsten Papenbrock. 2024. "JET: Fast Estimation of Hierarchical Time Series Clustering" Engineering Proceedings 68, no. 1: 37. https://doi.org/10.3390/engproc2024068037





