Modeling the Future of Hydroelectric Power: A Cross-Country Study †
Abstract
1. Introduction
2. Materials and Methods
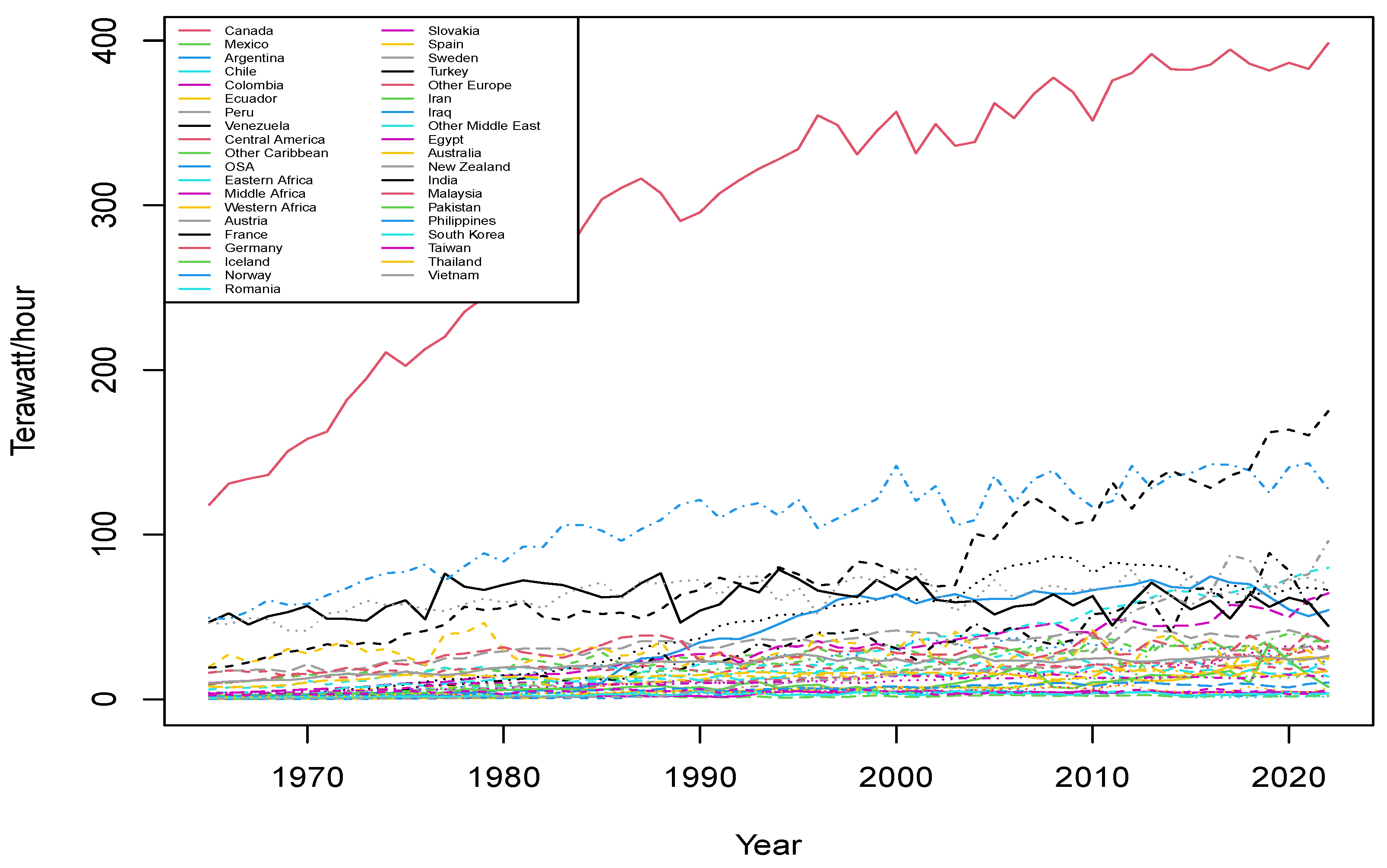
2.1. Data
2.2. Bass Model
2.3. Dynamic Market Potential
GGM
2.4. Prophet Model
2.5. Evaluation Metrics
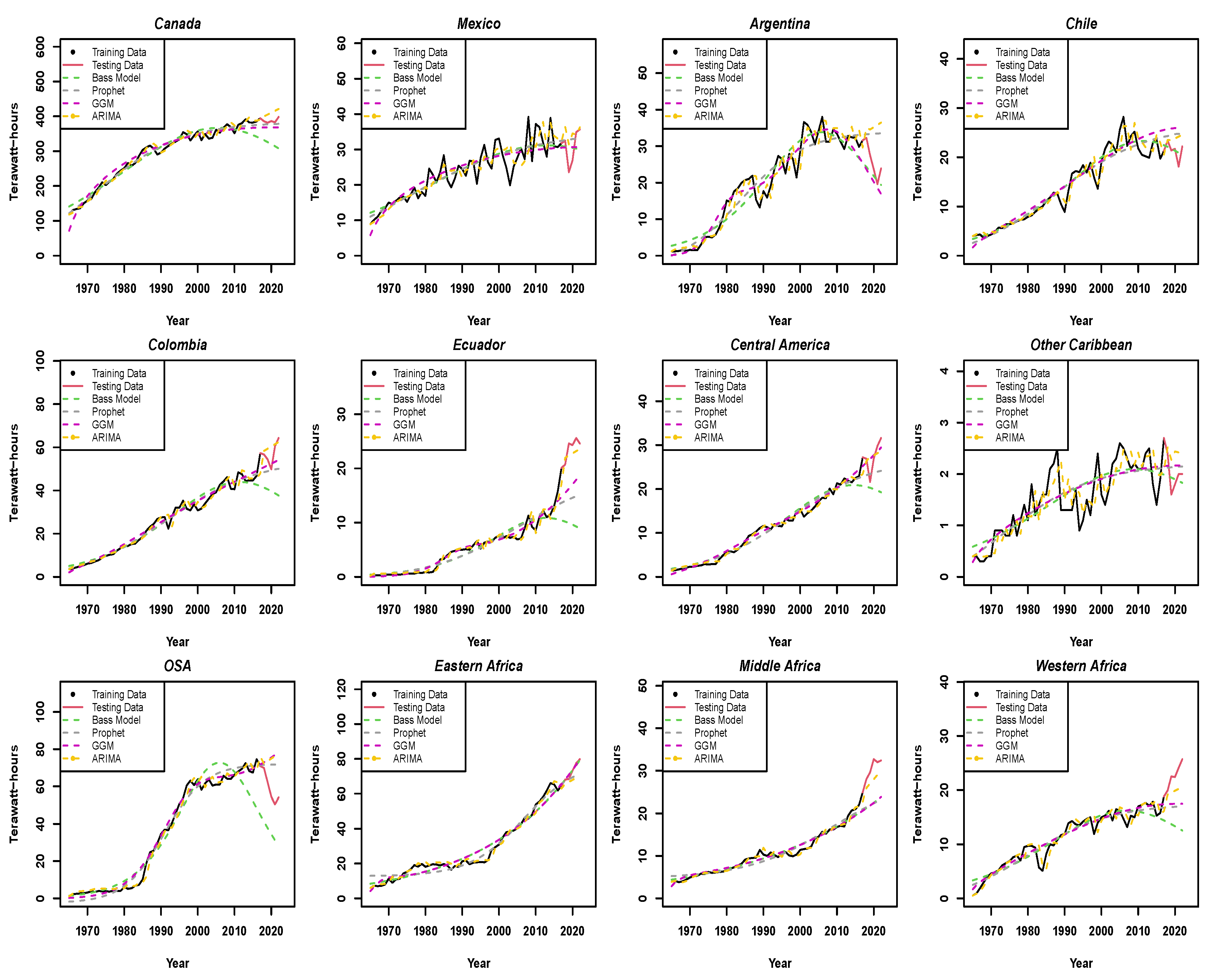
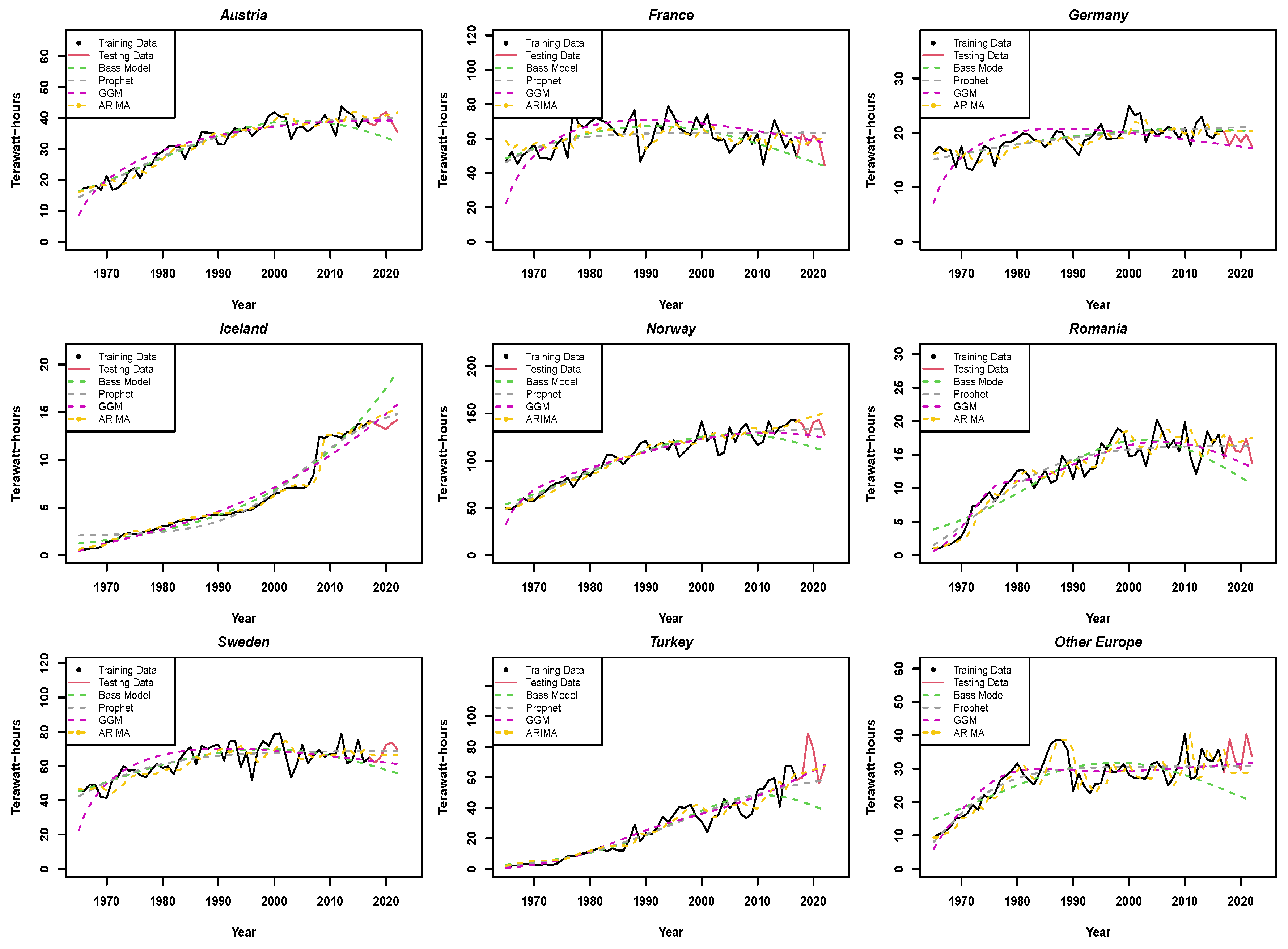
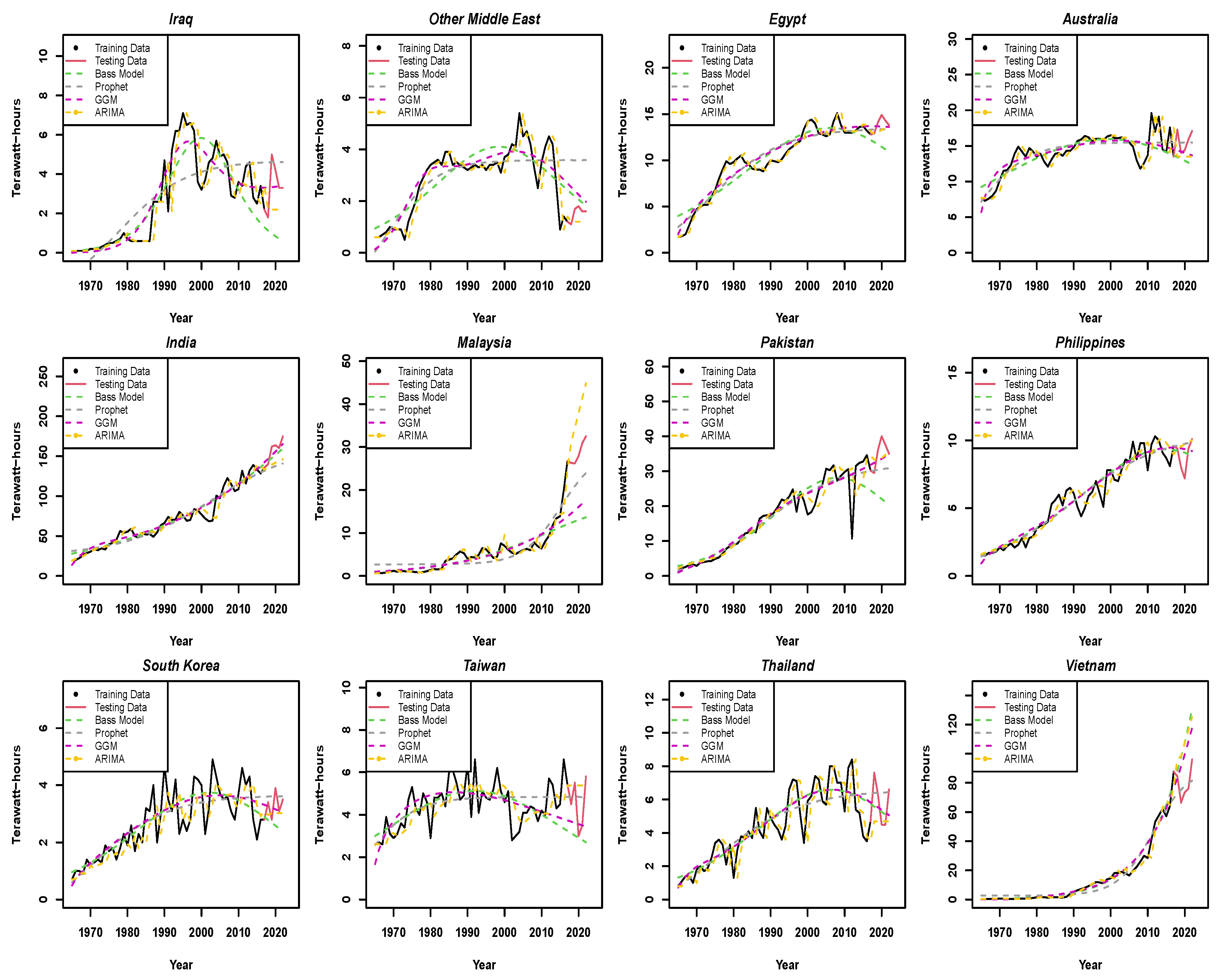
3. Results
3.1. American and South African Regions
3.2. European Regions
3.3. Asia and the Middle East
3.4. Evaluation Metrics
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- He, P.; Ni, X. Renewable Energy Sources in the Era of the Fourth Industrial Revolution: A Perspective of Civilization Development. J. Phys. Conf. Ser. 2022, 2301, 012030. [Google Scholar] [CrossRef]
- Malhotra, R. Fossil energy: Introduction. In Fossil Energy; Springer: New York, NY, USA, 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Savio, A.; Ferrari, G.; Marinello, F.; Pezzuolo, A.; Lavagnolo, M.C.; Guidolin, M. Developments in Bioelectricity and Perspectives in Italy: An Analysis of Regional Production Patterns. Sustainability 2022, 14, 15030. [Google Scholar] [CrossRef]
- de Freitas Cavalcanti, J.T.; de Lima, J.G.; do Nascimento Melo, M.R.; Monteiro, E.C.; Campos-Takaki, G.M. Fossil Fuels, Nuclear Energy and Renewable Energy; Seven Editora: São José, Brazil, 2023. [Google Scholar] [CrossRef]
- Kabeyi, M.J.; Olanrewaju, O.A. Sustainable energy transition for renewable and low carbon grid electricity generation and supply. Front. Energy Res. 2022, 9, 1032. [Google Scholar] [CrossRef]
- Bakis, R. The current status and future opportunities of hydroelectricity. Energy Sources Part B 2007, 2, 259–266. [Google Scholar] [CrossRef]
- Guseo, R.; Guidolin, M. Modelling a dynamic market potential: A class of automata networks for diffusion of innovations. Technol. Forecast. Soc. Chang. 2009, 76, 806–820. [Google Scholar] [CrossRef]
- Guidolin, M. Innovation Diffusion Models: Theory and Practice; John Wiley and Sons: Hoboken, NJ, USA, 2023. [Google Scholar]
- Taylor, S.J.; Letham, B. Forecasting at scale. Am. Stat. 2018, 72, 37–45. [Google Scholar] [CrossRef]
- Geem, Z.W.; Roper, W.E. Energy demand estimation of South Korea using artificial neural network. Energy Policy 2009, 37, 4049–4054. [Google Scholar] [CrossRef]
- Zhu, Q.; Guo, Y.; Feng, G. Household energy consumption in China: Forecasting with BVAR model up to 2015. In Proceedings of the 2012 Fifth International Joint Conference on Computational Sciences and Optimization, Harbin, China, 23–26 June 2012. [Google Scholar]
| Model | MAE | RMSE | MAPE |
|---|---|---|---|
| BM | 11.13 | 11.74 | 28.47 |
| GGM | 5.03 | 5.75 | 16.29 |
| Prophet | 5.41 | 6.12 | 20.63 |
| ARIMA | 5.51 | 6.28 | 16.43 |
| Prophet | ARIMA | BM | GGM | |
|---|---|---|---|---|
| Prophet | 0 | 19 | 28 | 13 |
| ARIMA | 21 | 0 | 30 | 15 |
| BM | 12 | 10 | 0 | 7 |
| GGM | 27 | 25 | 33 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, F.; Finos, L.; Guidolin, M. Modeling the Future of Hydroelectric Power: A Cross-Country Study. Eng. Proc. 2024, 68, 56. https://doi.org/10.3390/engproc2024068056
Ahmad F, Finos L, Guidolin M. Modeling the Future of Hydroelectric Power: A Cross-Country Study. Engineering Proceedings. 2024; 68(1):56. https://doi.org/10.3390/engproc2024068056
Chicago/Turabian StyleAhmad, Farooq, Livio Finos, and Mariangela Guidolin. 2024. "Modeling the Future of Hydroelectric Power: A Cross-Country Study" Engineering Proceedings 68, no. 1: 56. https://doi.org/10.3390/engproc2024068056
APA StyleAhmad, F., Finos, L., & Guidolin, M. (2024). Modeling the Future of Hydroelectric Power: A Cross-Country Study. Engineering Proceedings, 68(1), 56. https://doi.org/10.3390/engproc2024068056








