Minimization of Water Age in Water Distribution Systems under Uncertain Demand †
Abstract
:1. Introduction
2. Problem Formulation
3. The MCS-Based Probabilistic Analysis Problem
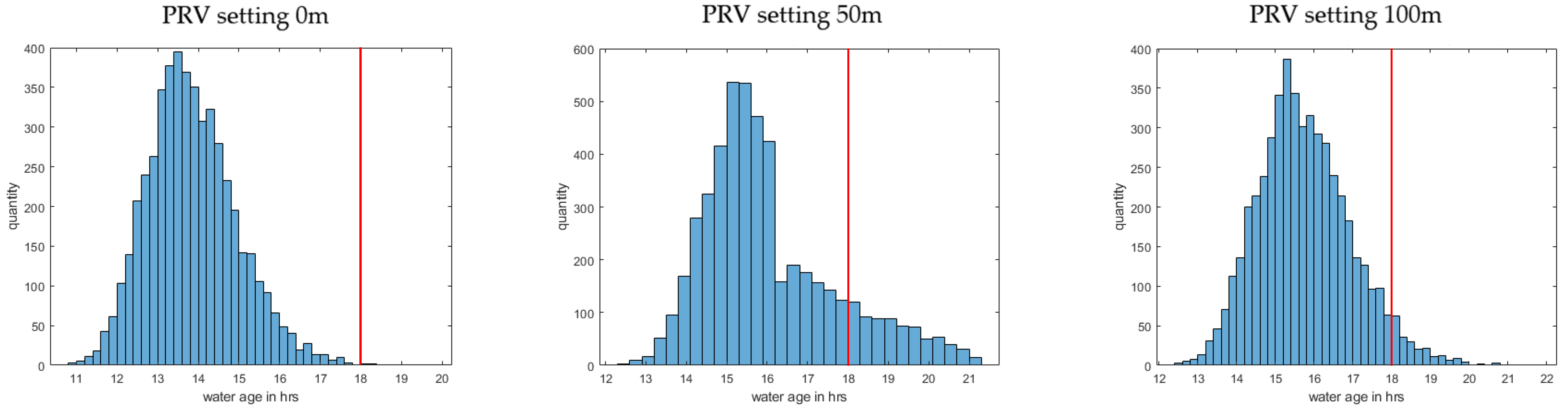
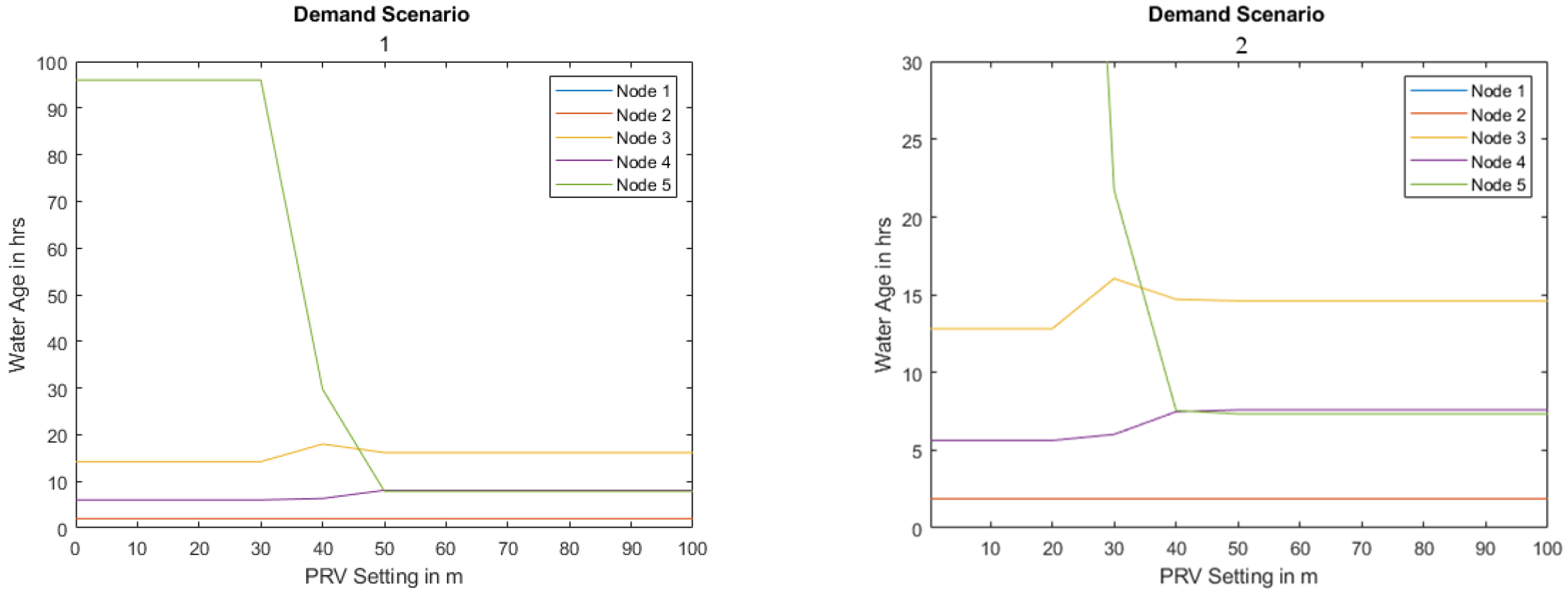
4. Case Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Office of Water (4606). Distribution System Water Quality—Maintaining a Disinfectant Residual. In Technical Report EPA/815/F-21/003; U.S. Environmental Protection Agency: Washington, DC, USA, 2021. [Google Scholar]
- Korder, K.; Cao, H.; Salomons, E.; Ostfeld, A.; Li, P. Simultaneous Minimization of Water Age and Pressure in WDS by PRVs. Water Resour. Manag. 2024, 38, 3561–3579. [Google Scholar] [CrossRef]
- Dandy, G.; Wu, W.; Simpson, A.; Leonard, M.A. Review of Sources of Uncertainty in Optimization Objectives of Water Distribution Systems. Water 2023, 15, 136. [Google Scholar] [CrossRef]
- Lansey, K.E.; Mays, L.W.; Tung, Y.-K. Water Distribution System Design Under Uncertainties. J. Water Resour. Plan. Manag. 1989, 115, 630–645. [Google Scholar] [CrossRef]
- Perelman, G.; Ostfeld, A. Adjustable Robust Optimization for Water Distribution System Operation Under Uncertainty. Water Resour. Res. 2023, 59, e2023WR035508. [Google Scholar] [CrossRef]
- Stuhlmacher, A.; Mathieu, J.L. Chance-Constrained Water Pumping to Manage Water and Power Demand Uncertainty in Distribution Networks. Proc. IEEE 2020, 108, 1640–1655. [Google Scholar] [CrossRef]
- Raza, N.; Moazeni, F. Chance-constrained vulnerability assessment of smart water distribution systems against stealthy false data injection attacks. Int. J. Crit. Infrastruct. Prot. 2024, 24, 100645. [Google Scholar] [CrossRef]
- Li, P. Prozessoptimierung unter Unsicherheiten, 1st ed.; Oldenbourg Wissenschaftsverlag: München, Germany, 2007. [Google Scholar] [CrossRef]
- Eliades, D.G.; Kyriakou, M.; Vrachimis, S.; Polycarpou, M.M. EPANET-MATLAB Toolkit: An Open-Source Software for Interfacing EPANET with MATLAB. In Proceedings of the 14th International Conference on Computing and Control for the Water Industry (CCWI), Amsterdam, The Netherlands, 7–9 November 2016. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Korder, K.; Salomons, E.; Ostfeld, A.; Li, P. Minimization of Water Age in Water Distribution Systems under Uncertain Demand. Eng. Proc. 2024, 69, 17. https://doi.org/10.3390/engproc2024069017
Korder K, Salomons E, Ostfeld A, Li P. Minimization of Water Age in Water Distribution Systems under Uncertain Demand. Engineering Proceedings. 2024; 69(1):17. https://doi.org/10.3390/engproc2024069017
Chicago/Turabian StyleKorder, Kristina, Elad Salomons, Avi Ostfeld, and Pu Li. 2024. "Minimization of Water Age in Water Distribution Systems under Uncertain Demand" Engineering Proceedings 69, no. 1: 17. https://doi.org/10.3390/engproc2024069017
APA StyleKorder, K., Salomons, E., Ostfeld, A., & Li, P. (2024). Minimization of Water Age in Water Distribution Systems under Uncertain Demand. Engineering Proceedings, 69(1), 17. https://doi.org/10.3390/engproc2024069017










