Optimal Location of Best Management Practices for Flood Mitigation in Urban Drainage Systems †
Abstract
1. Introduction
2. Methodology
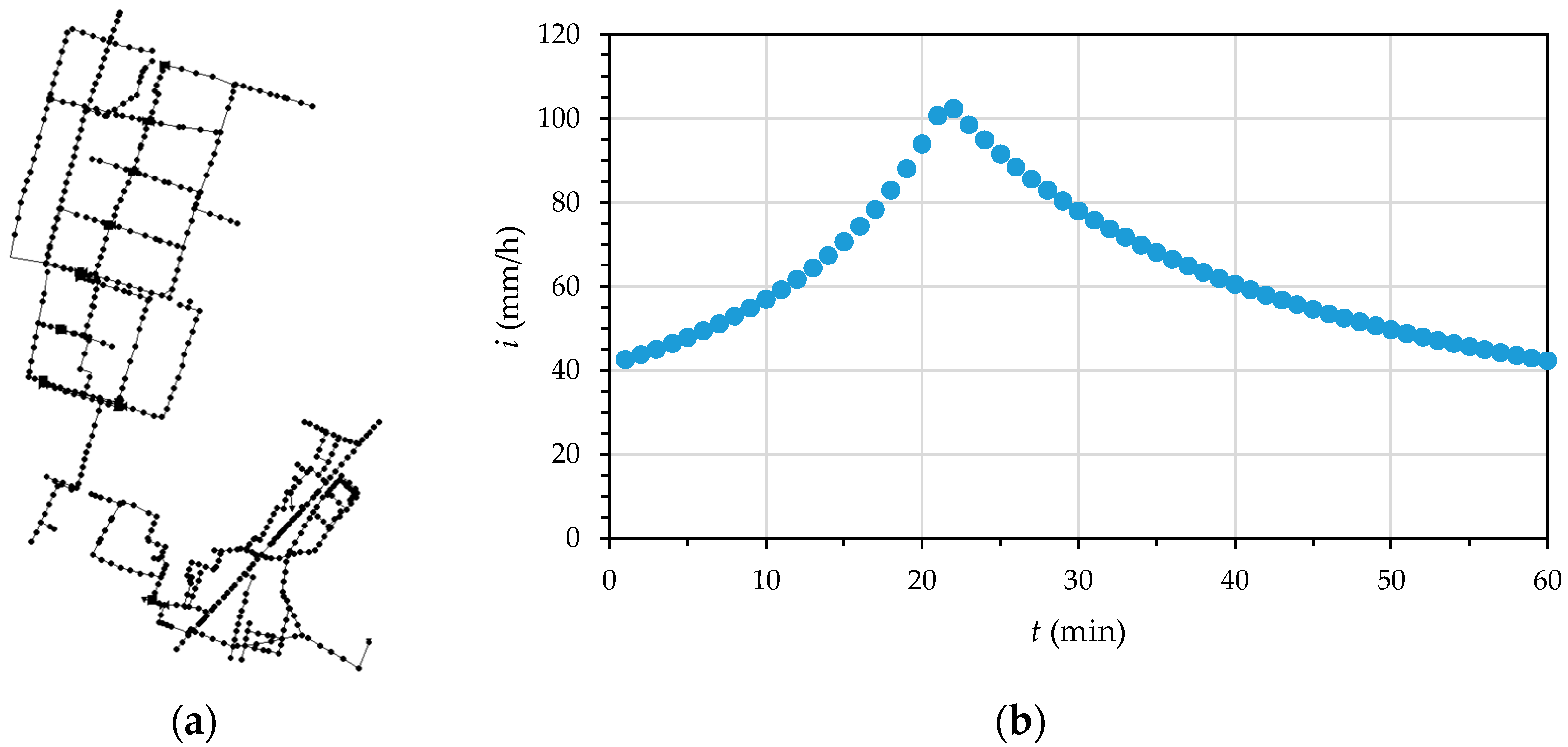
2.1. Hyetograph Construction
2.2. Urban Drainage Modeling
2.3. Optimization
3. Applications
3.1. Case Study
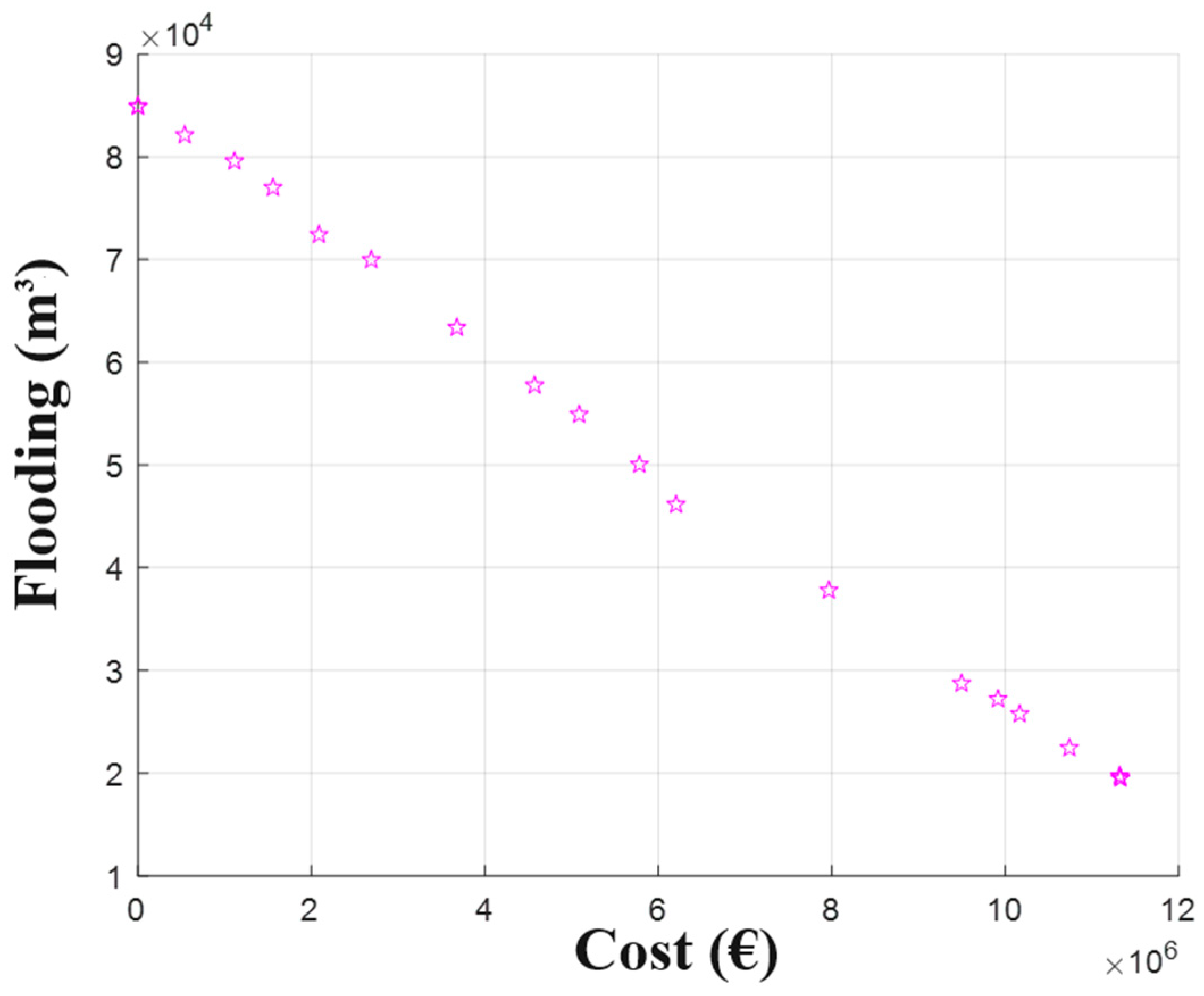
3.2. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- European Environment Agency. Urban Adaptation in Europe: How Cities and Towns Respond to Climate Change; EEA Report 12; European Environment Agency: Copenhagen, Denmark, 2020.
- Grossi, G.; Barontini, S.; Berteni, F.; Balistrocchi, M.; Ranzi, R. Nature-based solutions as climate change adaptation and mitigation measures in Italy. In Climate-Change Sensitive Water Resources Management; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Creaco, E. Scaling models of intensity–duration–frequency (IDF) curves based on adjusted design event durations. J. Hydrol. 2024, 632, 130847. [Google Scholar] [CrossRef]
- Kotz, S.; Nadarajah, S. Extreme Value Distributions: Theory and Applications; Imperial College Press: London, UK, 2000. [Google Scholar]
- Keifer, C.J.; Chu, H.H. Synthetic storm pattern for drainage design. J. Hydraul. Div. 1957, 83, 1–25. [Google Scholar] [CrossRef]
- Rossman, L.A. Storm Water Management Model User’s Manual Version 5.1.; EPA/600/R-14/413b; United States Environmental Protection Agency: Washington, DC, USA, 2015.
- Riaño-Briceño, G.; Barreiro-Gomez, J.; Ramirez-Jaime, A.; Quijano, N.; Ocampo-Martinez, C. MatSWMM—An open-source toolbox for designing real-time control of urban drainage systems. Environ. Model. Softw. 2016, 83, 143–154. [Google Scholar] [CrossRef]
- The MathWorks, Inc. Optimization Toolbox™ User’s Guide; The Math Works, Inc: Natick, MA, USA, 2024. [Google Scholar]
- Creaco, E.; Franchini, M.; Walski, T. Taking account of uncertainty in demand growth when phasing the construction of a water distribution network. J. Water Resour. Plan. Manag. 2014, 141, 04014049. [Google Scholar] [CrossRef]
| Climate Scenario | a1 | n | V | ξ | σ | μ | c |
|---|---|---|---|---|---|---|---|
| RCP 2.6 | 43.44 | −0.90 | 0.48 | 0.006 | 0.773 | −0.451 | 0.568 |
| RCP 4.5 | 39.38 | −0.90 | 0.46 | 0.023 | 0.755 | −0.454 | 0.568 |
| RCP 8.5 | 35.55 | −0.90 | 0.49 | 0.000 | 0.780 | −0.450 | 0.567 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Creaco, E.; Dada, A.; Grossi, G.; Todeschini, S. Optimal Location of Best Management Practices for Flood Mitigation in Urban Drainage Systems. Eng. Proc. 2024, 69, 189. https://doi.org/10.3390/engproc2024069189
Creaco E, Dada A, Grossi G, Todeschini S. Optimal Location of Best Management Practices for Flood Mitigation in Urban Drainage Systems. Engineering Proceedings. 2024; 69(1):189. https://doi.org/10.3390/engproc2024069189
Chicago/Turabian StyleCreaco, Enrico, Arianna Dada, Giovanna Grossi, and Sara Todeschini. 2024. "Optimal Location of Best Management Practices for Flood Mitigation in Urban Drainage Systems" Engineering Proceedings 69, no. 1: 189. https://doi.org/10.3390/engproc2024069189
APA StyleCreaco, E., Dada, A., Grossi, G., & Todeschini, S. (2024). Optimal Location of Best Management Practices for Flood Mitigation in Urban Drainage Systems. Engineering Proceedings, 69(1), 189. https://doi.org/10.3390/engproc2024069189









