An Analytical Solution for the Hydraulics of Looped Pipe Networks †
Abstract
1. Introduction
2. Materials and Methods
2.1. Modified Shortest-Path Algorithm
2.2. Analytical Method
3. Results and Discussion
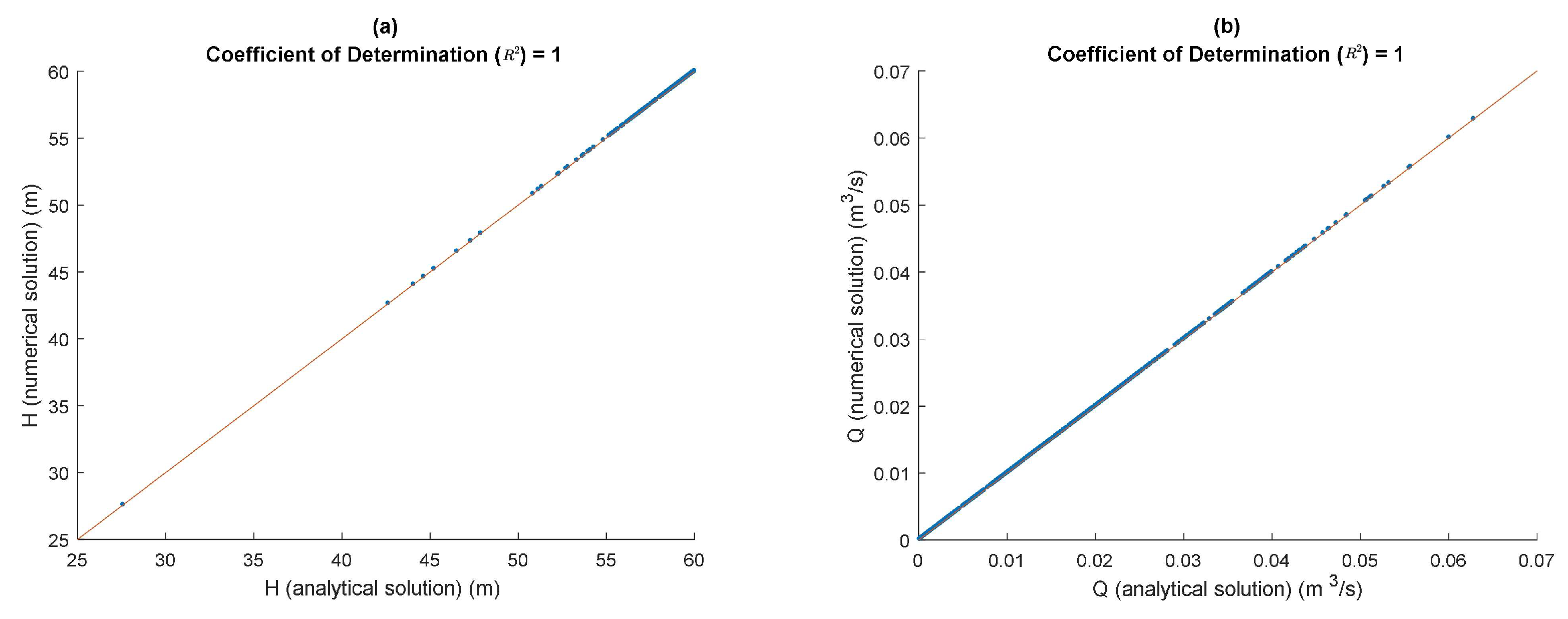
3.1. Single-Looped WDNs
3.2. Benchmark WDNs
3.3. Randomly Generated WDNs
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Todini, E.; Rossman, L.A. Unified framework for deriving simultaneous equation algorithms for water distribution networks. J. Hydraul. Eng. 2013, 139, 511–526. [Google Scholar] [CrossRef]
- Cross, H. Analysis of Flow in Networks of Conduits or Conductors; Engineering Experiment Station. Bulletin No. 286; University of Illinois: Champaign, IL, USA, 1936. [Google Scholar]
- Zhang, H.; Cheng, X.; Huang, T.; Cong, H.; Xu, J. Hydraulic analysis of water distribution systems based on fixed point iteration method. Water Resour. Manag. 2017, 31, 1605–1618. [Google Scholar] [CrossRef]
- Bazrafshan, M.; Gatsis, N.; Giacomoni, M.; Taha, A. A fixed-point iteration for steady-state analysis of water distribution networks. In Proceedings of the 2018 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Anaheim, CA, USA, 26–29 November 2018. [Google Scholar]
- Wang, S.; Taha, A.F.; Sela, L.; Giacomoni, M.H.; Gatsis, N. A New Derivative-Free Linear Approximation for Solving the Network Water Flow Problem With Convergence Guarantees. Water Resour. Res. 2020, 56, e2019WR025694. [Google Scholar] [CrossRef]
- Vasilic, Z.; Stanic, M.; Kapelan, Z.; Ivetic, D.; Prodanovic, D. Improved loop-flow method for hydraulic analysis of water distribution systems. J. Water Resour. Plan. Manag. 2018, 144, 04018012. [Google Scholar] [CrossRef]
- Giudicianni, C.; Herrera, M.; Di Nardo, A.; Greco, R.; Creaco, E.; Scala, A. Topological placement of quality sensors in water-distribution networks without the recourse to hydraulic modeling. J. Water Resour. Plan. Manag. 2020, 146, 04020030. [Google Scholar] [CrossRef]
- Kadu, M.S.; Gupta, R.; Bhave, P.R. Optimal design of water networks using a modified genetic algorithm with reduction in search space. J. Water Resour. Plan. Manag. 2008, 134, 147–160. [Google Scholar] [CrossRef]
- Riyahi, M.M.; Bakhshipour, A.E.; Haghighi, A. Probabilistic warm solutions-based multi-objective optimization algorithm, application in optimal design of water distribution networks. Sustain. Cities Soc. 2023, 91, 104424. [Google Scholar] [CrossRef]
- Giudicianni, C.; Herrera, M.; Di Nardo, A.; Oliva, G.; Scala, A. The faster the better: On the shortest paths role for near real-time decision making of water utilities. Reliab. Eng. Syst. Saf. 2021, 212, 107589. [Google Scholar] [CrossRef]
| WDNs | Accuracy of Directions (%) | |||
|---|---|---|---|---|
| Alprovits | 7 | 8 | 0.5 | 100 |
| Hanoi | 32 | 34 | 0.67 | 100 |
| Fossolo | 37 | 58 | 0.95 | 88.0 |
| Group | fs | Nnetwork | Average Accuracy of Directions (%) | Range of Direction Accuracy (%) |
|---|---|---|---|---|
| 1 | 0.50–0.90 | 225 | 94.40 | 78.8–100 |
| 2 | 0.91–0.95 | 221 | 90.60 | 80.8–100 |
| 3 | 0.95–0.97 | 189 | 88.41 | 80.0–95.9 |
| 4 | 0.97–0.98 | 164 | 87.04 | 77.6–96.1 |
| 5 | 0.97–0.98 | 148 | 85.67 | 75.4–93.5 |
| 6 | 0.980–0.983 | 53 | 84.85 | 78.0–88.6 |
| Summary | 0.50–0.983 | 1000 | 89.42 | 75.40–100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Riyahi, M.M.; Bakhshipour, A.E.; Giudicianni, C.; Dittmer, U.; Haghighi, A.; Creaco, E. An Analytical Solution for the Hydraulics of Looped Pipe Networks. Eng. Proc. 2024, 69, 4. https://doi.org/10.3390/engproc2024069004
Riyahi MM, Bakhshipour AE, Giudicianni C, Dittmer U, Haghighi A, Creaco E. An Analytical Solution for the Hydraulics of Looped Pipe Networks. Engineering Proceedings. 2024; 69(1):4. https://doi.org/10.3390/engproc2024069004
Chicago/Turabian StyleRiyahi, Mohammad Mehdi, Amin E. Bakhshipour, Carlo Giudicianni, Ulrich Dittmer, Ali Haghighi, and Enrico Creaco. 2024. "An Analytical Solution for the Hydraulics of Looped Pipe Networks" Engineering Proceedings 69, no. 1: 4. https://doi.org/10.3390/engproc2024069004
APA StyleRiyahi, M. M., Bakhshipour, A. E., Giudicianni, C., Dittmer, U., Haghighi, A., & Creaco, E. (2024). An Analytical Solution for the Hydraulics of Looped Pipe Networks. Engineering Proceedings, 69(1), 4. https://doi.org/10.3390/engproc2024069004









