Real-Time Demand Forecasting and Multi-Resolution Model Predictive Control for Water Distribution Networks †
Abstract
1. Introduction
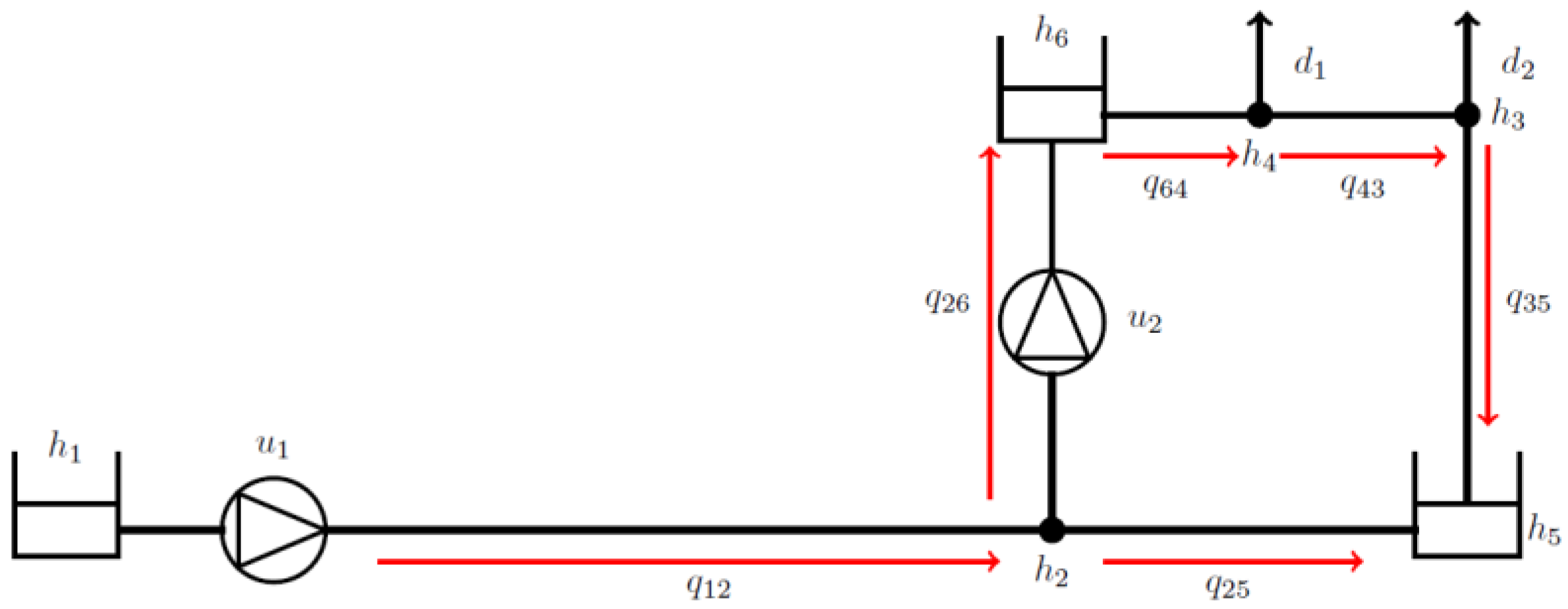
2. Control Architecture with Demand Prediction
Demand Estimation Using Artificial Intelligence
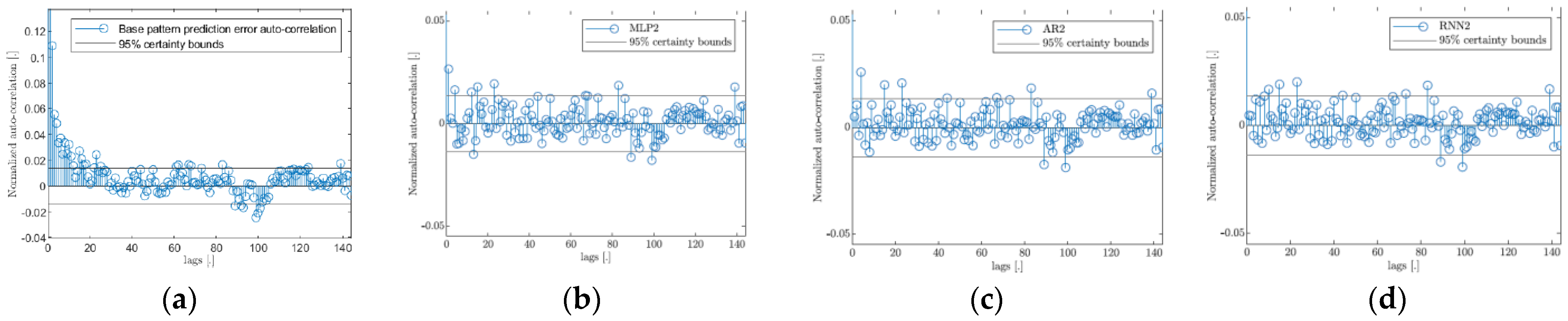
3. Results
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Y.; Puig, V.; Cembrano, G. Non-linear economic model predictive control of water distribution networks. J. Process Control. 2017, 56, 23–34. [Google Scholar] [CrossRef]
- Castelletti, A.; Ficchì, A.; Cominola, A.; Segovia, P.; Giuliani, M.; Wu, W.; Lucia, S.; Ocampo-Martinez, C.; Schutter, B.D.; Maestre, J.M. Model predictive control of water resources systems: A review and research agenda. ARC 2023, 55, 442–465. [Google Scholar] [CrossRef]
- Blokker, E.J.M.; Pieterse-Quirijns, E.J.; Vreeburg, J.H.G.; Van Dijk, J.C. Simulating Nonresidential Water Demand with a Stochastic End-Use Model. J. WRPM 2011, 137, 511–520. [Google Scholar] [CrossRef]
- Bakker, M.; Vreeburg, J.H.G.; van Schagen, K.M.; Rietveld, L.C. A fully adaptive forecasting model for short-term drinking water demand. Environ. Model. Softw. 2013, 48, 141–151. [Google Scholar] [CrossRef]
- Verheijen, P.C.N.; Lazar, M.; Goswami, D. Efficient Implementation and Sampling Period Analysis of MPC for Water Distribution Networks. IFAC papersOnline 2022, 55, 42–47. [Google Scholar] [CrossRef]
- de Groot, W.P. Nonlinear Demand Prediction for Model Predictive Control of Water Distribution Networks. Master Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 17 July 2023. [Google Scholar]
| Auto-Regressive (AR) | Recurrent Neural Network (RNN) | Multi-Layer Perceptron (MLP) |
|---|---|---|
| 10 min Sampling Period | Multi-Resolution Sampling Period | |||||
|---|---|---|---|---|---|---|
| Exact | Base Only | Base + AR | Exact | Base Only | Base + AR | |
| cost | 70,658 | 70,765 | 70,777 | 70,663 | 70,770 | 70,782 |
| cost | 157.3 | 164.8 | 176.5 | 158.5 | 165.5 | 176.9 |
| cost | 4616 | 9002 | 7447 | 4821 | 9413 | 7790 |
| Solver time | 1.58s | 1.56s | 1.57s | 0.34s | 0.34s | 0.34s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Verheijen, P.C.N.; de Groot, W.P.; Goswami, D.; Lazar, M. Real-Time Demand Forecasting and Multi-Resolution Model Predictive Control for Water Distribution Networks. Eng. Proc. 2024, 69, 70. https://doi.org/10.3390/engproc2024069070
Verheijen PCN, de Groot WP, Goswami D, Lazar M. Real-Time Demand Forecasting and Multi-Resolution Model Predictive Control for Water Distribution Networks. Engineering Proceedings. 2024; 69(1):70. https://doi.org/10.3390/engproc2024069070
Chicago/Turabian StyleVerheijen, Peter C. N., Ward P. de Groot, Dip Goswami, and Mircea Lazar. 2024. "Real-Time Demand Forecasting and Multi-Resolution Model Predictive Control for Water Distribution Networks" Engineering Proceedings 69, no. 1: 70. https://doi.org/10.3390/engproc2024069070
APA StyleVerheijen, P. C. N., de Groot, W. P., Goswami, D., & Lazar, M. (2024). Real-Time Demand Forecasting and Multi-Resolution Model Predictive Control for Water Distribution Networks. Engineering Proceedings, 69(1), 70. https://doi.org/10.3390/engproc2024069070






