Predicting Contamination Spreading in Water Distribution Networks †
Abstract
1. Introduction
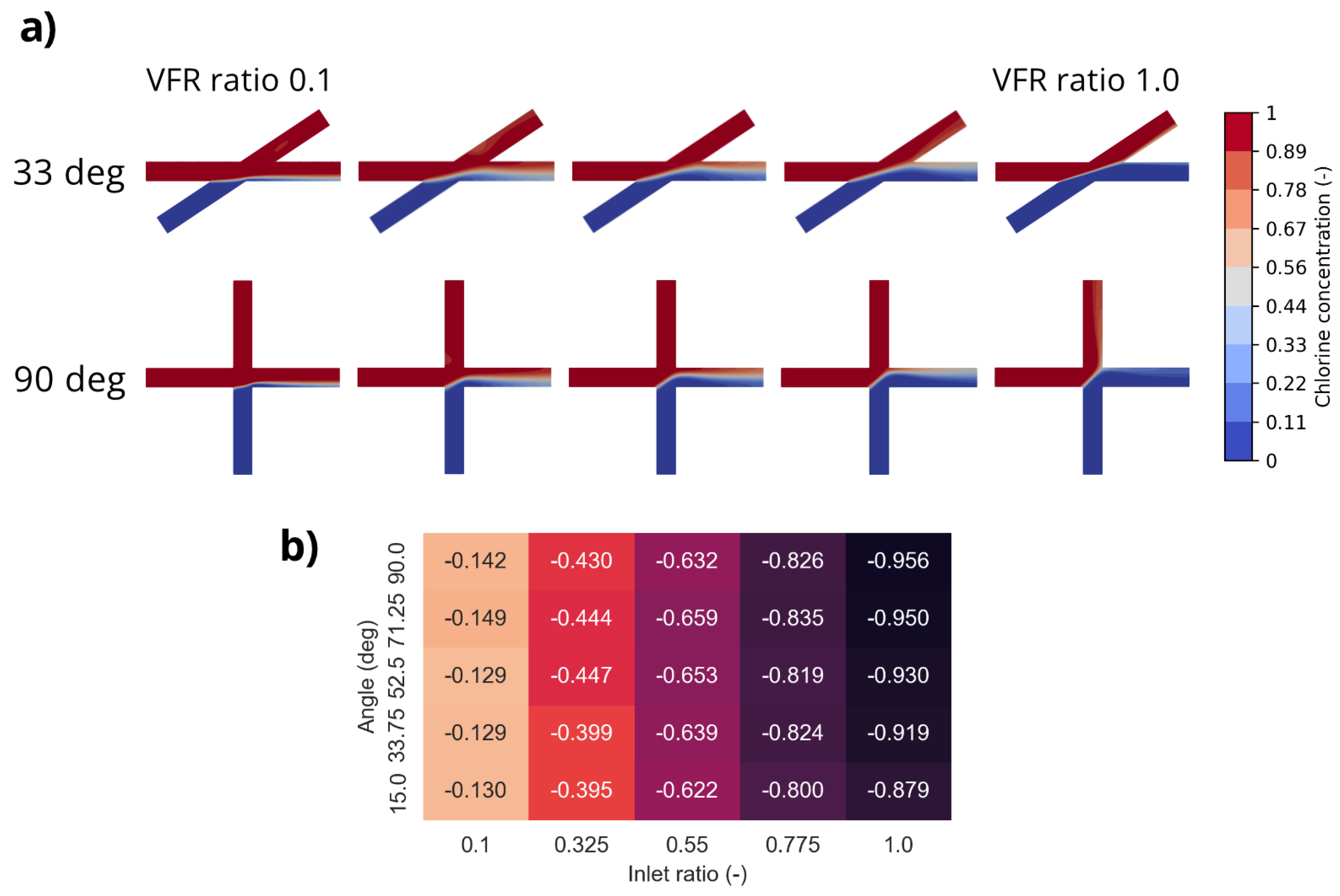
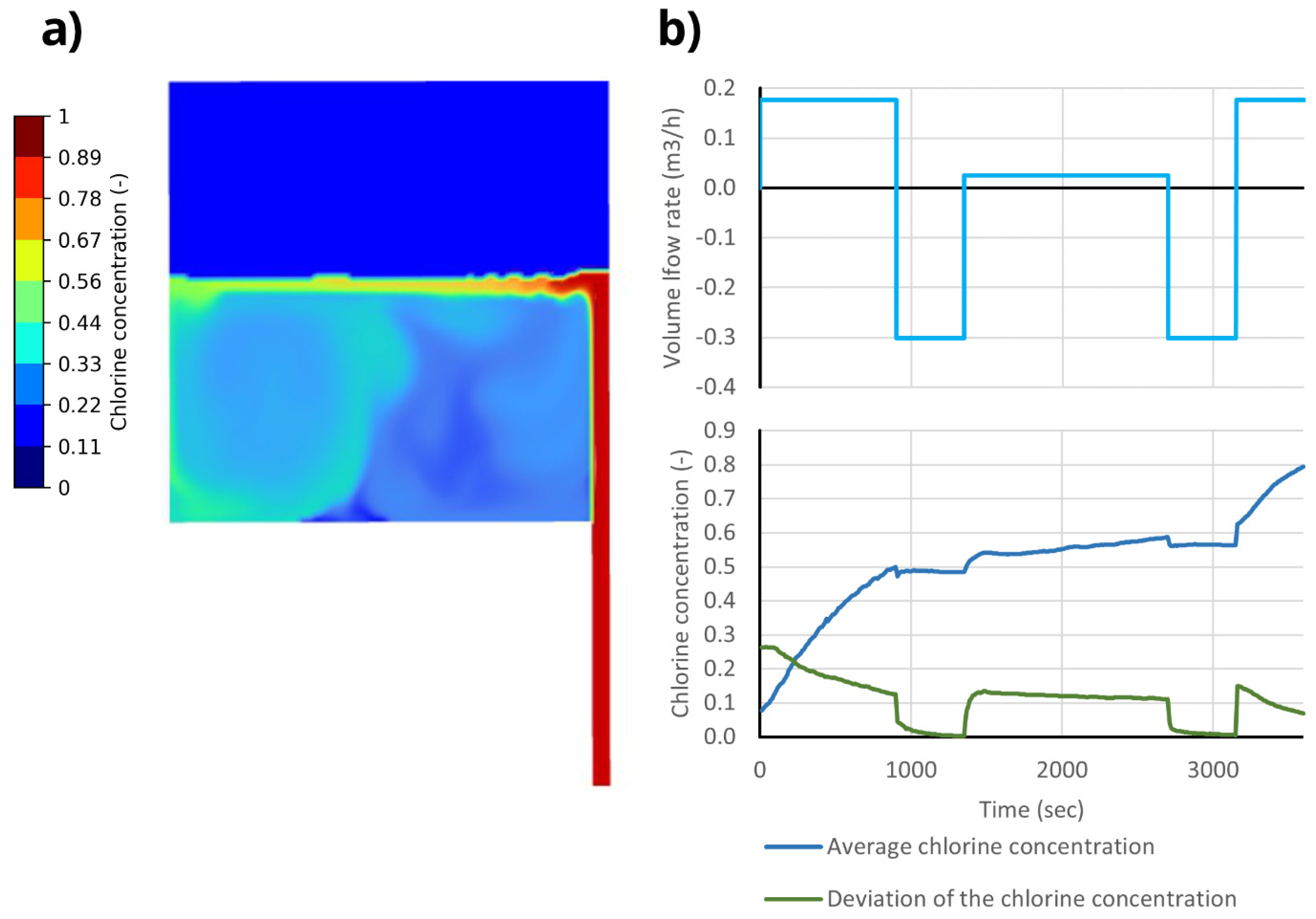
2. Materials and Methods
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ho, C.K.; Orear, L.; Wright, J.L.; Mckenna, S.A. Contaminant Mixing at Pipe Joints: Comparison Between Laboratory Flow Experiments and Computational Fluid Dynamics Models. In Proceedings of the Water Distribution Systems Analysis Symposium, Cincinnati, OH, USA, 27–30 August 2006. [Google Scholar]
- Austin, R.G.; Van Bloemen Waanders, B.; Mckenna, S.; Choi, C.Y. Mixing at Cross Junctions in Water Distribution Systems. II: Experimental Study. J. Water Resour. Plan. Manag. 2008, 134, 295–302. [Google Scholar] [CrossRef]
- Yu, T.C.; Shao, Y.; Shen, C. Mixing at Cross Joints with Different Pipe Sizes in Water Distribution Systems. J. Water Resour. Plan. Manag. 2014, 140, 658–665. [Google Scholar] [CrossRef]
- Yousefian, R.; Duchesne, S. Improving incomplete mixing modeling for junctions of water distribution networks. J. Hydroinformatics 2024, 26, 351–367. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wéber, R.; Sándor, L.; Horváth, Á.; Barakka, G.; Abhijith, G.R.; Ostfeld, A. Predicting Contamination Spreading in Water Distribution Networks. Eng. Proc. 2024, 69, 96. https://doi.org/10.3390/engproc2024069096
Wéber R, Sándor L, Horváth Á, Barakka G, Abhijith GR, Ostfeld A. Predicting Contamination Spreading in Water Distribution Networks. Engineering Proceedings. 2024; 69(1):96. https://doi.org/10.3390/engproc2024069096
Chicago/Turabian StyleWéber, Richárd, Levente Sándor, Ákos Horváth, Gábor Barakka, Gopinathan R. Abhijith, and Avi Ostfeld. 2024. "Predicting Contamination Spreading in Water Distribution Networks" Engineering Proceedings 69, no. 1: 96. https://doi.org/10.3390/engproc2024069096
APA StyleWéber, R., Sándor, L., Horváth, Á., Barakka, G., Abhijith, G. R., & Ostfeld, A. (2024). Predicting Contamination Spreading in Water Distribution Networks. Engineering Proceedings, 69(1), 96. https://doi.org/10.3390/engproc2024069096






