Mechanical Characterization of Ultra-Violet-Curable Resin-Based Polymer Foams Containing Triply Periodic Minimal Surface Lattice Structures ^†

Abstract

Triply periodic minimal surface lattice structures are three-dimensional arrays of complex cells that can only be efficiently manufactured by 3D printing. The mechanical properties of these lattice structures depend on lattice parameters such as cell sizes along the X, Y, and Z axes, and wall thickness. Designing such lattice structures for soft polymers permits the manufacturing of polymer foams with controllable mechanical stiffnesses. The objective of this work is to design and 3D print polymeric foams made of lattice structures and evaluate the effect of lattice parameters on the resulting stiffness. Lattice parameters define the lattice geometry and stiffness. Ten specimens with different lattice parameters were designed and 3D printed using a low-cost desktop liquid crystal display 3D printer using ultra-violet-curable resin. Then, following ASTM D3574-17, these samples were subjected to compression tests. An experimental analysis was conducted to examine the deformation characteristics of these structures, focusing on parameters such as yield strain, initial stiffness, and the maximum force at 50% compression.

1. Introduction

Originally, humankind constructed robust edifices utilizing materials such as concrete and steel. But then they realized that by using the natural properties of materials like wood, which have cellular structures and very small gaps between cells, they could not only make the foams more rigid and last longer, but also recieve other benefits that would make them more useful. This led to more uses being identified for foams [1]. During the early twenty-first century, concerns about climate change led to the replacement of foam with paper-based alternatives in food and beverage packaging. As a result, foam shifted from being a prominent primary material to a discreet component used for supportive functions, such as in mattresses [2].

Foams are porous polymeric materials that can be produced by either physically foaming them using a physical blowing agent such as supercritical CO2, or chemically foaming them using a chemical blowing agent that thermally decomposes or creates crosslinks to release a gas [3]. Foams have remarkable characteristics such as being resilient and lightweight, and having rigidity, a high porosity, and crushability, as well as compression, energy absorption, cushioning, and impact resistance. These attributes contribute to its great performance in various industrial applications [4,5]. Polymeric foams have found use in several industries such as sports, healthcare, medicine, electronics, bedding, insulation, automobile, furniture, engineering, interior design, and cosmetics due to their ability to decrease weight and tailor mechanical and functional properties [6]. Optimizing foam density is essential for certain applications, as parameters like compressive stresses and density optimization have a considerable influence on the mechanical and functional characteristics of foams, especially in lightweight construction [7]. Elastomeric foam is the preferred choice for bedding applications due to its capacity to be restored to its initial shape even when exposed to external pressures. This highlights the significance of foams in managing compressive forces in various sectors, including packaging and vehicle cushioning [8].

Polyurethane, a widely used foam in various applications, is composed of two main components: polyol and isocyanate. The polyol serves as the flexible element of the polymer, while the isocyanate enables the formation of the rigid portion [9]. The wide range of mechanical qualities exhibited by polyurethane, including flexibility, semi-flexibility, and stiffness, make it very desirable in multiple industries such as cushioning, footwear, and seat padding. The distinctive blend of features, such as its adaptability and porous composition, offers notable benefits in these specific uses [10]. The inherent randomness and uncertain internal structure of foam materials present disadvantages, highlighting the significance of understanding microscopic characteristics when evaluating foam substitutes [11]. The production of lattice structures, which imitate three-dimensional mesoscale building blocks, allows for flexibility and the ability to perform various tasks, leading to the desired properties [12]. Manipulating mesoscale characteristics at the cellular level enables the development of durable structures capable of withstanding substantial stresses while minimizing material usage. These structures also encompass sophisticated capabilities, such as effective energy absorption and heat dissipation [13,14].

The versatility in material selection and the capability to manufacture items on demand hold the potential to transform traditional manufacturing techniques [15]. Researchers have also sought to identify reliable alternatives, recognizing the substantial impact of the microstructure on the overall behavior and characteristics of foam materials. The creation of these structures entails the duplication of mesoscale unit cells in three dimensions [16]. This enables a significant amount of design adaptability in altering the shapes of the unit cells and attaining desired material properties at the macroscopic level. Due to their adaptability, these structures are well-suited for a diverse array of applications. However, the process of producing these intricate lattice structures can be challenging when employing conventional production techniques, highlighting the necessity for advanced manufacturing technologies [17].

Rossiter et al. [18] studied how five geometric design choices affected the plateau stress and energy capacity of lattice structures to predict compression behavior. A factorial design and analysis of variance were used to identify design variables that significantly affected lattice structure compression. Strut cross-sectional area (CSA) and cell width exhibited the biggest effects on the plateau stress and energy capacity of lattice structures, highlighting their importance in compression behavior. However, Rifaie et al. [19] conducted quasi-static compression tests to determine the stiffness, failure loads, and energy absorption of four polymer lattice configurations. They found stiffness, failure loads, and strain energy absorption discrepancies across the four lattice topologies under compression loading.

Mishra et al. [20] compared the Schwarz-P TPMS lattice structures using both PLA and ABS materials at different degrees of compression and found that both materials deformed differently when the strain rate was varied. First, the peak stress increased linearly with the strain rate, with the PLA samples showing an increase up to 30% greater than ABS. Although the stress-strain plots indicated substantial variance between the materials evaluated at the same rate of deformation, the Schwarz-P surface-based TPMS lattices exhibited linear energy absorption. Furthermore, Syrlybayev et al. [21] tested hybrid lattice structures for compression by conducting quasi-static compression experiments, recording failure modes with a digital camera, and computing displacement from the frames. They calculated elastic modulus, yield stress, yield strain, densification strain, and energy absorption efficiency.

Isaenkova et al. [22] investigated the compression behavior of lattice systems by conducting compression tests in various orientations and assessing the relationship between stress and strain. Their findings suggest that the lattice structure exhibits anisotropic behavior during deformation. In quasi-static compression tests, Dar et al. [23] found that the number of unit cells significantly affects lattice compression properties, with smaller cells resulting in better elastic stiffness, strength, and energy absorption. The simulation projected stress–strain curves that matched the experimental curves.

The researchers in [24] studied the compression characteristics of lattice structures through finite element analysis. They observed non-linear behavior and failure events such as plastic hinges in the joints and elastoplastic buckling of vertical struts. Furthermore, Amani et al. [25] inspected the compression characteristics of lattice structures by fabricating two face-centered cubic structures with varying dimensions of struts and nodes through the application of selective laser melting (SLM) technology. The deformation of the structures under compression was visualized using in situ and ex situ X-ray tomography scanning.

Park et al. [26] examined the compression characteristics of lattice structures through the implementation of compression tests. They observed the deformation behaviors, established the yield and densification points, and computed the densification strain using energy absorption efficiency. The researchers conducted an experimental analysis to examine the deformation behaviors and determined the densification strain for each lattice configuration.

Through an in-depth review of past research and literature, we have discovered that lattice architectures provide an enhanced design freedom. This is achieved by replicating mesoscale unit cells to attain the appropriate material properties. Additive Manufacturing is the primary technique used to achieve the effective creation of intricate lattice structures. The objective of this paper is to develop soft polymeric constructs that may be used to evaluate the stiffness of lattice materials. The mechanical properties of lattice components are greatly influenced by the lattice geometries, which are governed by lattice parameters.

Later, these designs were realized using a UV Resin Photocuring Printer for use in compression tests. An investigation was conducted to examine the parameters of deformation in these constructions, specifically focusing on factors such as yield point, initial stiffness, and the maximum force experienced at 50% compression. To evaluate the influence of these characteristics on the structural stiffness of lattice elements, 10 lattice parts were manufactured, incorporating volume fraction and lattice type. The study sought to investigate the impact of specific lattice features on their stiffness, and the following alterations that arose from this investigation.

2. Materials and Methods

2.1. Design

The design part of this work utilized nTopology (nTop) version 4.0.5, which was operated under a non-commercial license. Ten lattice unit cells were precisely fabricated, with each cell exhibiting distinct volume fractions of 30% and 50% through variations in cell size and wall thickness. The task entailed creating samples through 3D printing, using unit cells drawn from 5-walled triply periodic minimal surfaces (WTPMS). The surfaces represented in Figure 1 are Diamond, Gyroid, Lindinoid, Schwarz, and SplitP, respectively. Afterwards, the lattice cells were incorporated into a three-dimensional structure with dimensions of 50 × 50 × 25 mm³. The body comprised two surfaces, one positioned at the upper and the other at the lower end of a part, both with a uniform thickness of 2 mm. The incorporation of two surfaces in this configuration enhances the robustness and accuracy of the compression testing.

Table 1. The configuration of the 10 samples 3D printed in this study.

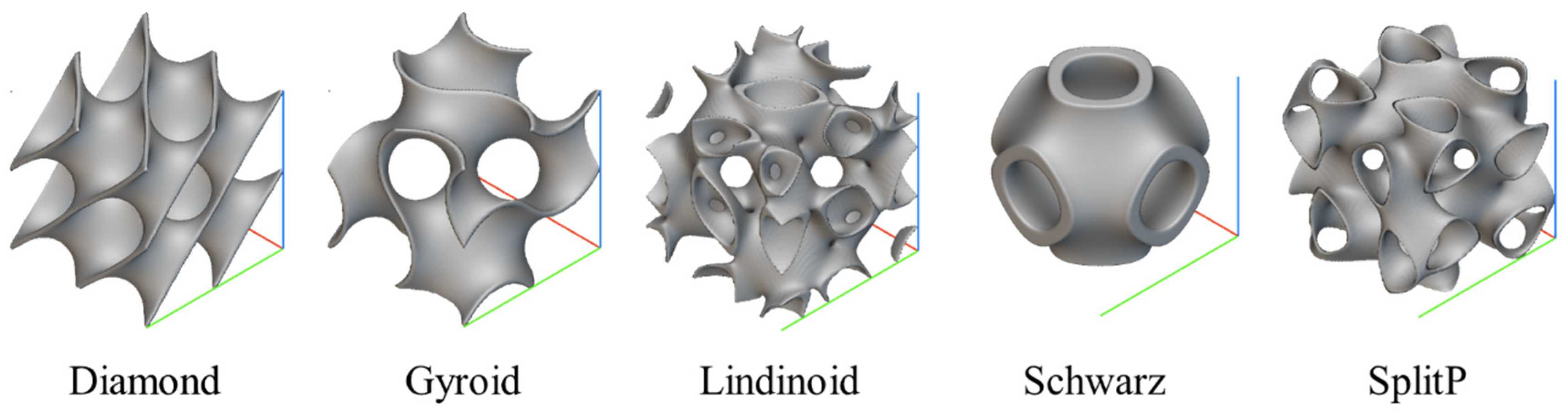
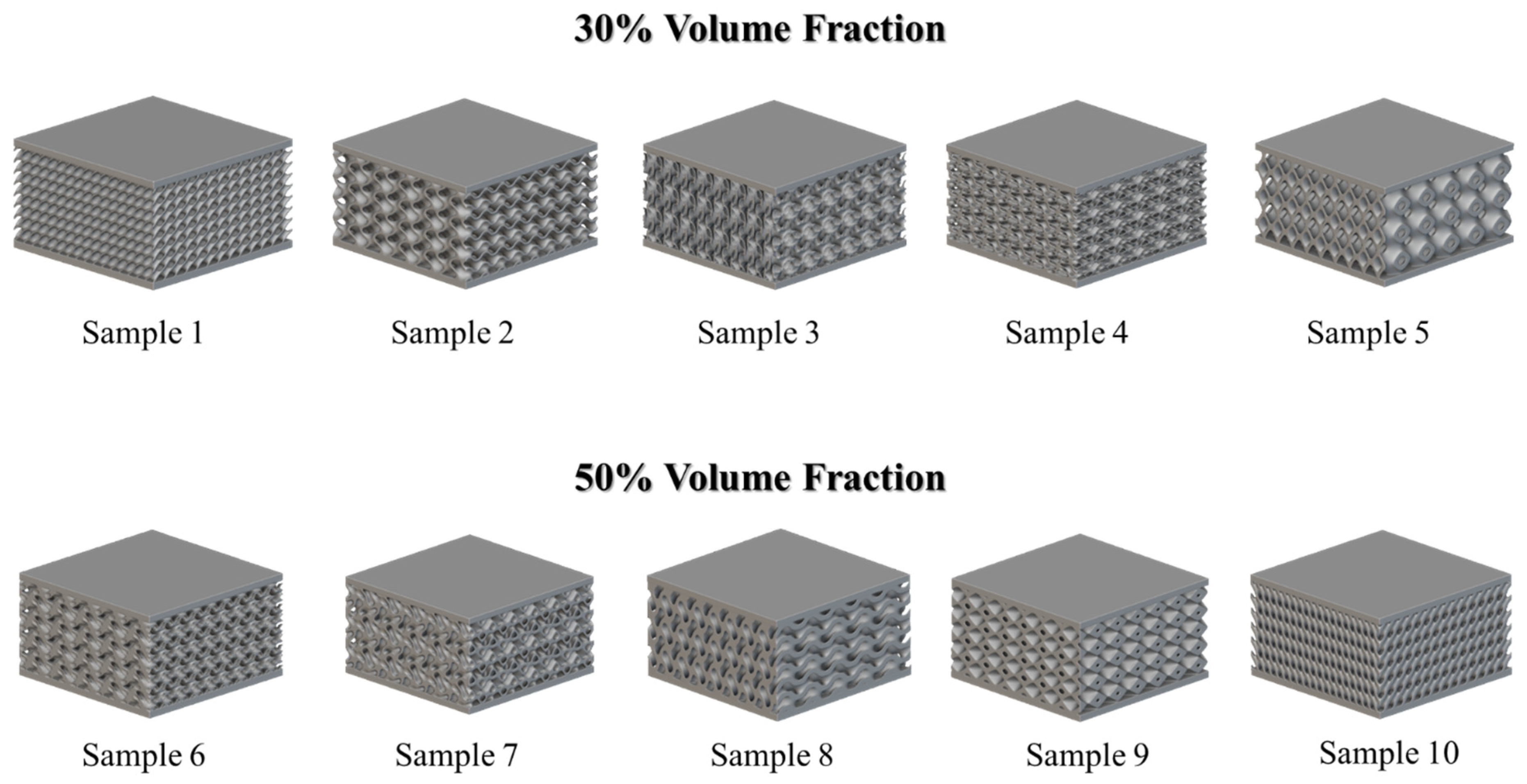
Sample	Lattice Type	X (mm)	Y (mm)	Z (mm)	Thickness (mm)	Volume Fraction
1	Diamond	6.2	7.7	6.0	0.8	30
2	Gyroid	9.5	6.3	5.9	1.1
3	Lidinoid	6.3	7.6	7.8	0.6
4	SplitP	9.5	8.6	5.2	0.9
5	Schwarz	5.5	9.6	8.0	0.7
6	Lidinoid	9.7	5.6	5.8	1.1	50
7	SplitP	9.6	8.5	9.4	1.8
8	Gyroid	6.3	9.8	8.0	2.1
9	Schwarz	7.3	7.8	5.1	1.0
10	Diamond	5.1	6.9	8.3	1.5

displays the results of this investigation, indicating that 10 samples were printed. Each lattice type was printed with volume fractions of 30% and 50%, and the cell size and thickness were also altered. Furthermore, Figure 2 depicts the nTop view of them.

2.2. Additive Manufacturing

The CHITUBOX Basic v1.9.4 software, F80 Elastic Gingival-like Resin material, ELEGOO Mars 3 Pro 4K 3D printer, and the Anycubic Wash and Cure Plus Machine were employed in this work to generate nTop files. The selection of these tools was based on their flawless compatibility, which guarantees smooth component manufacturing and the production of stress–strain curves.

CHITUBOX Basic v1.9.4 is a widely used 3D printing slicing software that offers a user-friendly interface, extensive printer compatibility, and robust functionalities. The software is compatible with several file types and allows users to modify parameters such as layer thickness, infill density, and print speed.

The F80 Elastic Gingival-like Resin was chosen as the material for this study due to its unique qualities, which make it very adaptable and well suited to a range of applications. This resin has a Shore Hardness of 50–60 A, which gives it a flexible texture and excellent elasticity. This allows it to quickly regain its original shape after being deformed, which helps to prolong its lifespan. Despite cold temperatures below 10 °C, the F80 resin remains soft, but it may experience a slight decrease in elasticity. This makes it adaptable for different environments and uses throughout the year.

This study employed specific print parameters optimized for F80 Gingival-like Resin, adhering to the recommended configuration for the ELEGOO MARS 3 PRO 3D printer. The parameters, including Layer Height, Exposure Time, Bottom Exposure Time, and others, were established based on this particular configuration.

The post-processing stage in 3D printing is both demanding and crucial. The dependability and durability of the printed component are crucial in this stage. The Anycubic Wash and Cure Plus Machine effectively cleans and solidifies resin components by rotating the immersed part in alcohol. The duration required to clean the lattice structures in the Anycubic machine using clean alcohol varies depending on the specific lattice configuration. After the drying process was completed, the objects were subjected to curing using an Anycubic machine. UV lights in this machine can cure the parts from the top and all of their sides by rotating the part. Upon completion of the curing process, the components were prepared for use in compression testing, as depicted in Figure 3.

2.3. Compression Test

The ASTM D3574-17 [27] Compression Force Deflection technique was utilized to evaluate the distortions of the lattice structures created through 3D printing. The Instron 5969 Universal Testing Machine applied a force of 50 kilonewtons to the samples during the test. The machine exhibited a deflection rate of 600 mm/min by utilizing a force-measuring device and a flat compression foot that exceeded the size of the specimen and remained stationary. The ASTM D3574-17 parameters were configured with the Instron machine. The magnitude of the force was quantified for lattice sample tops that were crushed by 50%. The samples, including both the top and bottom surfaces, had measurements of 50 mm by 50 mm by 29 mm, following the guidelines set by the ASTM standard. The specimens underwent compression at a velocity of 50 mm/min, leading to a decrease in their thickness by 50% (14.5 mm). The magnitude of the force applied during this procedure was quantified in Newton units. Figure 4 illustrates the relationship between force and displacement in each compression test, as shown by the curve.

3. Result and Discussion

The yield point (εy), Young’s modulus (k), and maximum force (Fmax) for each force displacement curve were determined and are displayed in

Table 2. Yield point, Young’s modulus, and maximum force for each samples based on their force displacement curves.

Lattice Type	Volume Fraction = 30%			Volume Fraction = 50%
	εy (%)	k (N/mm)	Fmax (N)	εy (%)	k (N/mm)	Fmax (N)
Diamond	3.37	4.5283	422.1011	6.51	15.442	2394.9089
Gyroid	4.04	3.6397	287.8259	2.44	15.458	1060.1224
Lidinoid	2.11	1.8592	206.6092	5.97	16.011	1637.1638
Schwarz	1.71	11.749	407.1946	6.77	7.6923	634.6938
SplitP	4.04	2.4217	290.6495	5.31	13.764	1147.599

. This table reveals that the link between Young’s modulus and volume fraction in lattice systems offers valuable insights into their mechanical features. Regarding the lattice type, there is a continuous and proportional increase in Young’s modulus when the volume fraction increases from 30% to 50%. This occurrence emphasizes a fundamental principle in the domain of material science. Structures that have a higher density typically exhibit greater stiffness. The reason for this trend is the rising material density within the lattice, resulting in more frequent atomic interactions and an enhanced resistance to deformation caused by external pressures. The congruity between our empirical observations and theoretical predictions enhances the dependability of our outcomes.

Moreover, the Gyroid lattice exhibits a significant augmentation in Young’s modulus within the volume fractions of 30% to 50%, warranting careful evaluation. The substantial increase emphasizes the powerful influence of volume fraction on the mechanical properties of lattice structures. This suggests that even slight changes in the volume fraction can lead to substantial fluctuations in stiffness, illustrating the intricate dependence of material behavior on geometric parameters.

Understanding these subtle differences in the variability in Young’s modulus enables engineers and material scientists to make informed decisions when constructing lattice-based components. By adjusting the volume fraction, it is possible to precisely control the stiffness of the lattice in order to meet specific performance requirements. This includes enhancing the ability to bear loads, maximizing energy absorption, and ensuring structural integrity in demanding applications. The Diamond lattice exhibits a substantial increase in the yield point as the volume fraction rises from 30% to 50%, indicating that denser configurations have enhanced structural resilience. This behavior aligns with the intuitive notion that an increase in material density results in an increase in resistance to plastic deformation.

Conversely, the Schwarz lattice displays a clear pattern, indicating a reduction in the yield point as the volume fraction grows from 30% to 50%. This unexpected phenomenon suggests that there is a nuanced response to changes in the proportion of volume, which may be influenced by unique geometric factors inherent to the Schwarz lattice structure. Further investigation into the underlying mechanisms responsible for this behavior could provide valuable insights for improving lattice designs for certain applications.

The diverse mechanical responses exhibited by different lattice designs underscore the importance of considering the specific characteristics of each lattice when designing materials for specific purposes. The Lidinoid lattice has an exceptional rigidity at different volume fractions, despite its comparatively low yield point, indicating an excellent balance between strength and stiffness. This finding emphasizes the flexibility of the Lidinoid structure, making it a desirable choice for scenarios that demand both a strong stiffness and a moderate resistance to deformation. Conversely, the SplitP lattice exhibits a moderate degree of stiffness while maintaining stable yield points regardless of the volume fractions. This behavior demonstrates a higher level of consistency in responding to changes in volume percentage, which can be advantageous in situations where predictability and stability are crucial.

To summarize, the information gathered from our analysis highlights the need to consider the volume proportion and specific attributes of the lattice when designing materials for different technical applications. By applying this knowledge, researchers and engineers can modify lattice structures to achieve certain mechanical properties, hence facilitating the investigation of new opportunities for progress in several fields.

4. Conclusions

To summarize, this study examines the mechanical characteristics of lattice structures, with specific emphasis on the impact of geometric factors and volume fraction on their response to compression. The study methodically analyzes different lattice configurations at varying volume fractions, providing valuable insights into their unique reactions to external forces. A significant discovery is the clear relationship between Young’s modulus and volume fraction in all lattice types, emphasizing the importance of material density in producing structural rigidity. Furthermore, the need to take into account specific geometric variables when designing materials for specific purposes is emphasized by the subtle differences in yield points seen among the various lattice types.

To obtain a better understanding of the mechanical properties of lattice systems, it would be beneficial to investigate the influence of additional geometric parameters, apart from volume fraction, in future research. In addition, the incorporation of sophisticated computational methods, like machine learning or finite element analysis, has the potential to improve the accuracy of lattice design predictions. This, in turn, would enable the creation of customized materials with specific mechanical characteristics.