Comparative Analysis of Field Oriented Control and Direct Torque Control Through Simulation in MATLAB Simulink for an Automotive Drive Motor †
Abstract
1. Introduction
2. Materials and Methods
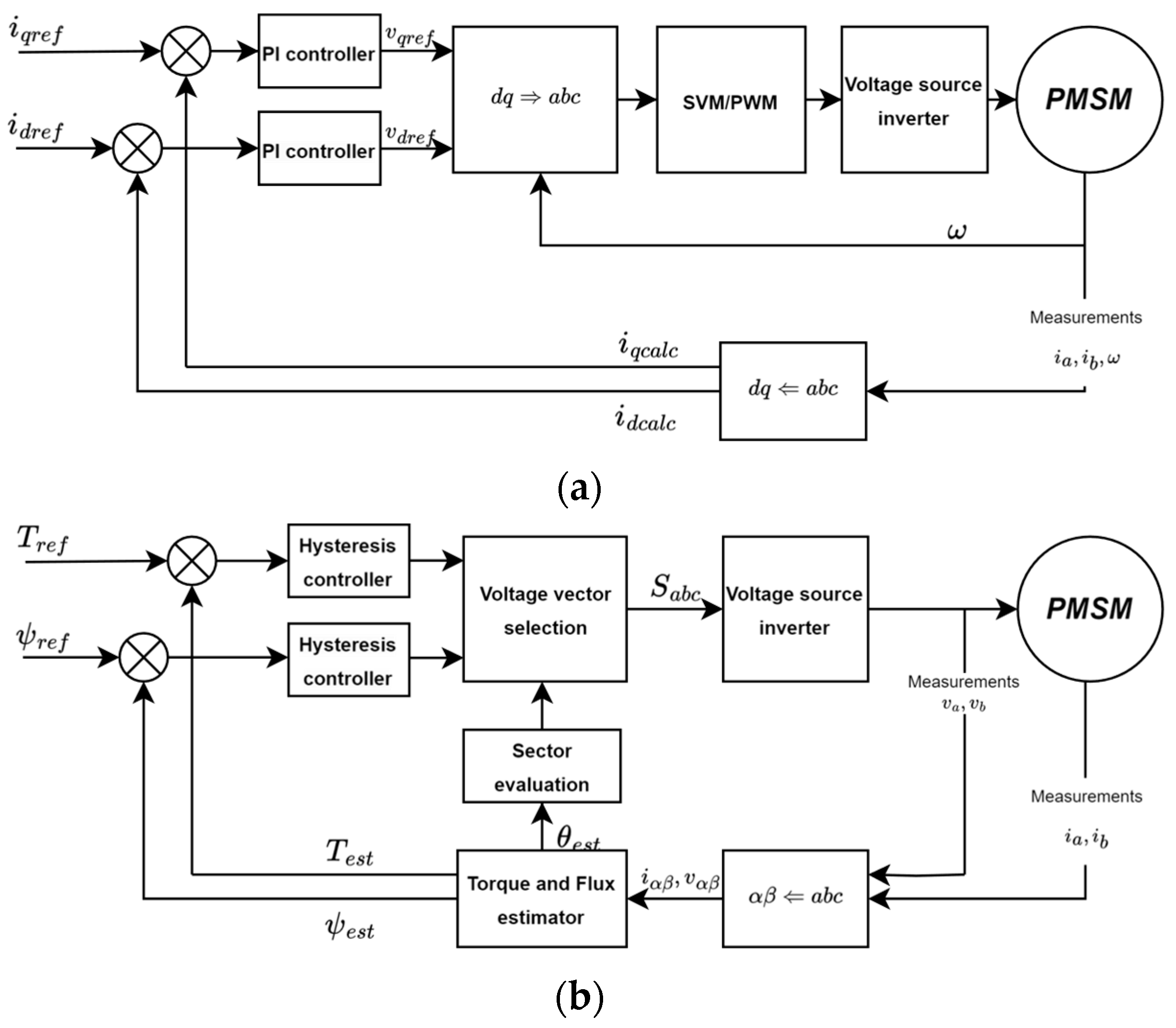
2.1. The Background Used for FOC
2.2. The Model for DTC
2.3. Comparison of the Models
2.3.1. Similarities
- The control method used in both cases is torque reference-based. This type of control represents the use in an automotive traction motor most accurately. Drivers control the speed of a vehicle by pressing on the accelerator pedal, thereby demanding torque from the drive. The desired end result is speed, but that is controlled by the driver as an external loop in the system.
- Both models use the same VSI and the PMSM. Motor data can be found in Table 2.
- Both rely on coordinate transformation.
2.3.2. Differences
- FOC utilizes PWM to create the desired voltage vector, DTC does not have one in the original concept.
- FOC thereby also has a constant switching frequency, whereas DTCs change depending on the state of the hysteresis controllers.
- FOC has coordinate transformations from a–b–c to α–β to d–q, which is needed for the control of the current, whereas DTC has only an a–b–c to α–β conversion.
- FOC needs position information to carry out the d–q transformation; this is solved by a sensor in most cases, whereas DTC does not require this.
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Drive to Electrify. Nat. Clim. Chang. 2024, 14, 299. [CrossRef]
- Machhour, Z.; Mrabet, M.E.; Mekrini, Z.; Boulaala, M. Electric Motors and Control Strategies for Electric Vehicles: A Review. In Proceedings of the International Conference on Advanced Intelligent Systems for Sustainable Development, AI2SD 2022; Kacprzyk, J., Ezziyyani, M., Balas, V.E., Eds.; Lecture Notes in Networks and Systems; Springer: Cham, Switzerland, 2023; Volume 714, pp. 293–301. [Google Scholar]
- Kakodia, S.K.; Panda, A.K.; Dyanamina, G. Comparative Analysis of Speed Control Methods for PMSM Drive Fed Electrical Vehicle. In Proceedings of Flexible Electronics for Electric Vehicles; Dwivedi, S., Singh, S., Tiwari, M., Shrivastava, A., Eds.; Lecture Notes in Electrical Engineering; Springer: Singapore, 2023; Volume 863, pp. 313–321. [Google Scholar]
- Biyani, V.; Jinesh, R.; Tharani Esvar, T.A.; Sithartha Sourya, V.S.; Pinkymol, K.P. Vector Control Implementation in PMSM Motor Drive for Electric-Vehicle Application. In Proceedings of the 4th International Conference on Energy, Power, and Environment (ICEPE), Shillong, India, 29 April–1 May 2022; pp. 1–8. [Google Scholar] [CrossRef]
- Ramesh, P.; Umavathi, M.; Bharatiraja, C.; Ramanathan, G.; Athikkal, S. Development of a PMSM Motor Field-Oriented Control Algorithm for Electrical Vehicles. Mater. Today Proc. 2022, 65, 176–187. [Google Scholar] [CrossRef]
- Blaschke, F. Das Verfahren Der Feldorientierung Zur Regelung Der Drehfeldmaschine. Ph.D. Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 1973. [Google Scholar]
- Takahashi, I.; Noguchi, T. A New Quick-Response and High-Efficiency Control Strategy of an Induction Motor. IEEE Trans. Ind. Appl. 1986, IA-22, 820–827. [Google Scholar] [CrossRef]
- Tiitinen, P.; Surandra, M. The next Generation Motor Control Method, DTC Direct Torque Control. In Proceedings of the International Conference on Power Electronics, Drives and Energy Systems for Industrial Growth, New Delhi, India, 8–11 January 1996; Volume 1, pp. 37–43. [Google Scholar]
- Tiitinen, P.; Pohjalainen, P.; Lalu, J. The Next Generation Motor Control Method: Direct Torque Control (DTC). EPE J. 1995, 5, 14–18. [Google Scholar] [CrossRef]
- Europe Nissan News. Available online: https://europe.nissannews.com/en-GB/releases/release-a9f393adfcdb4c875b17ca02b001a9dc-nissan-brings-excitement-from-the-road-to-the-track-with-leaf-nismo-rc-unleashed-for-the-first-time-in-europe?selectedTabId=releases (accessed on 4 July 2024).
- Mathworks. Available online: https://se.mathworks.com/help/sps/powersys/ref/permanentmagnetsynchronousmachine.html (accessed on 4 July 2024).
- Park, R.H. Two-Reaction Theory of Synchronous Machines Generalized Method of Analysis-Part I. Trans. Am. Inst. Electr. Eng. 1929, 48, 716–727. [Google Scholar] [CrossRef]
- Oak Ridge National Laboratory Nissan Leaf Disassembly Data. Available online: https://openinverter.org/wiki/images/5/52/Em61_motor.png (accessed on 4 July 2024).
- Rodríguez, J.; Kennel, R.M.; Espinoza, J.R.; Trincado, M.; Silva, C.A.; Rojas, C.A. High-Performance Control Strategies for Electrical Drives: An Experimental Assessment. IEEE Trans. Ind. Electron. 2012, 59, 812–820. [Google Scholar] [CrossRef]
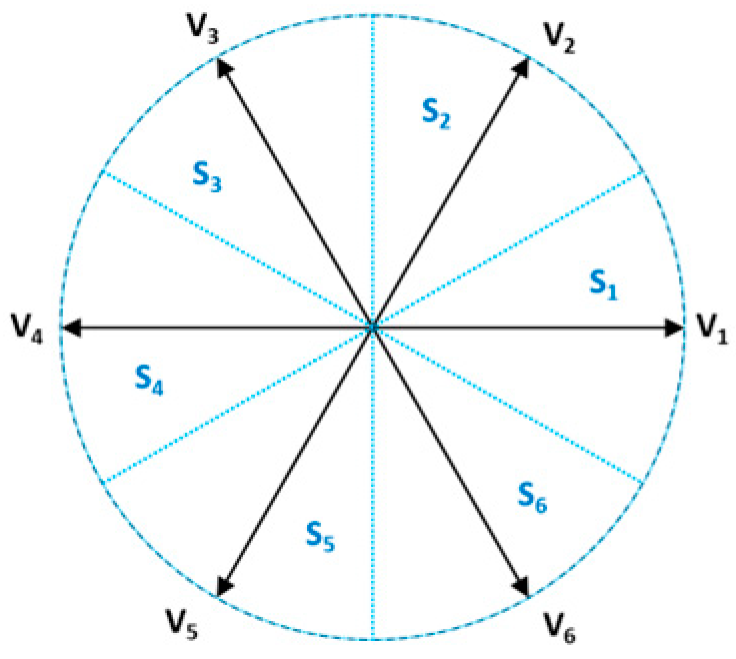

| Flux | Torque | S1 | S2 | S3 | S4 | S5 | S6 |
|---|---|---|---|---|---|---|---|
| + | + | V2 | V3 | V4 | V5 | V6 | V1 |
| + | - | V6 | V1 | V2 | V3 | V4 | V5 |
| - | + | V3 | V4 | V5 | V6 | V1 | V2 |
| - | - | V5 | V6 | V1 | V2 | V3 | V4 |
| Name | Marking | Data | Dimension |
|---|---|---|---|
| Quadrature Inductance | Lq | 4.3 | mH |
| Direct Inductance | Ld | 1.6 | mH |
| Flux Linkage | λm | 73 | mWb |
| Stator Resistance | RS | 23 | mΩ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simon, M.G.; Fodor, D. Comparative Analysis of Field Oriented Control and Direct Torque Control Through Simulation in MATLAB Simulink for an Automotive Drive Motor. Eng. Proc. 2024, 79, 33. https://doi.org/10.3390/engproc2024079033
Simon MG, Fodor D. Comparative Analysis of Field Oriented Control and Direct Torque Control Through Simulation in MATLAB Simulink for an Automotive Drive Motor. Engineering Proceedings. 2024; 79(1):33. https://doi.org/10.3390/engproc2024079033
Chicago/Turabian StyleSimon, Miklós Gábor, and Dénes Fodor. 2024. "Comparative Analysis of Field Oriented Control and Direct Torque Control Through Simulation in MATLAB Simulink for an Automotive Drive Motor" Engineering Proceedings 79, no. 1: 33. https://doi.org/10.3390/engproc2024079033
APA StyleSimon, M. G., & Fodor, D. (2024). Comparative Analysis of Field Oriented Control and Direct Torque Control Through Simulation in MATLAB Simulink for an Automotive Drive Motor. Engineering Proceedings, 79(1), 33. https://doi.org/10.3390/engproc2024079033






