A Prediction of Drug Transport, Distribution, and Absorption Through a Multicompartmental Physiologically Based Pharmacokinetic Model ^†

Abstract

The objective of this study was to develop a multicompartmental physiologically based pharmacokinetic (PBPK) model that allows for the reproduction of the function of the gastrointestinal system in silico. Based on the typical tools of chemical engineering, transport phenomena, and human physiological and anatomical knowledge, the developed model is not limited to representing the transport of drugs and their interactions with ingested foods but also describes several physiological aspects that quantitatively regulate the distribution, absorption, and elimination of drugs. Nevertheless, the model only contains a limited number of parameters: the permeability constants of jejunum, ileum, and colon membranes and the drug removal rates in both the blood and cellular compartments. Therefore, it can be used for a preliminary drug bioavailability assessment in the early stages of drug development when limited experimental data are available. The model was tested on two drugs, Ketoprofen and Ibuprofen, which yielded satisfactory results in accordance with the existing literature.

1. Introduction

The most common route of drug administration is the oral route due to the ease of administration compared to the intravenous, intramuscular, or subcutaneous routes [1,2]. However, oral drug administration leads to low or variable bioavailability, i.e., the fraction of the drug that reaches the systemic circulation [3]. Considering also the inter-individual differences in drug metabolism, specifically in the liver and gut [4], it is crucial to develop tools that can assess bioavailability throughout the drug development process. In this context, there has been a notable increase in the use of mathematical models, exploiting in vitro assays to provide in vivo insights [5]. In most cases, drug bioavailability modeling is conducted through physiologically based pharmacokinetic (PBPK) models, in which the organism is represented by one or more compartments that are variously interconnected [6,7]. PBPK models provide a mechanistic approach to study and predict the pharmacokinetics of drugs based on physiological and anatomical characteristics, as well as the physical and chemical properties of a given drug. The initial development of these tools was in the field of pharmaceuticals, and they have since been applied in a number of other areas, including pharmacology, drug development, drug discovery, and preclinical support [8,9].

Given this background, this study aims to develop a multicompartmental mathematical model, overcoming some simplifications adopted in previous works [10,11]. This approach, of course, introduces additional complexity to the model, but it also results in a more accurate representation of the gastrointestinal system (GIS), thereby facilitating more precise in silico evaluations of drug bioavailability. In particular, the proposed model incorporates some fundamental physiological processes that affect drug bioavailability, such as (i) the interactions between drug and food, (ii) the effect of bile salts produced by the liver, (iii) the kinetics of active transport of drugs in the intestinal lumen, and (iv) the first-pass effect of the liver. However, the higher degree of complexity of the model does not markedly affect the computational burden, enabling a rapid preliminary bioavailability assessment during the initial stages of drug development. The model was evaluated on two common active pharmaceutical ingredients (APIs), i.e., Ketoprofen and Ibuprofen, with data sourced from DrugBank [12]. The results are encouraging, demonstrating a high degree of concordance between the experimental and simulated data pertaining to the drug’s bioavailability over time.

2. Materials and Methods

The model was developed using a bottom-up approach, whereby each component of the system was defined separately before the interconnections were established to describe their interactions. This resulted in the creation of eleven compartments, which were treated either as well-stirred or hollow fiber reactors. Each compartment is characterized by a set of differential equations (both ordinary and partial differential equations), which were solved using Euler’s finite difference methods [13], and implemented in MATLAB R2023b. A schematic view of the proposed model is presented in Figure 1.

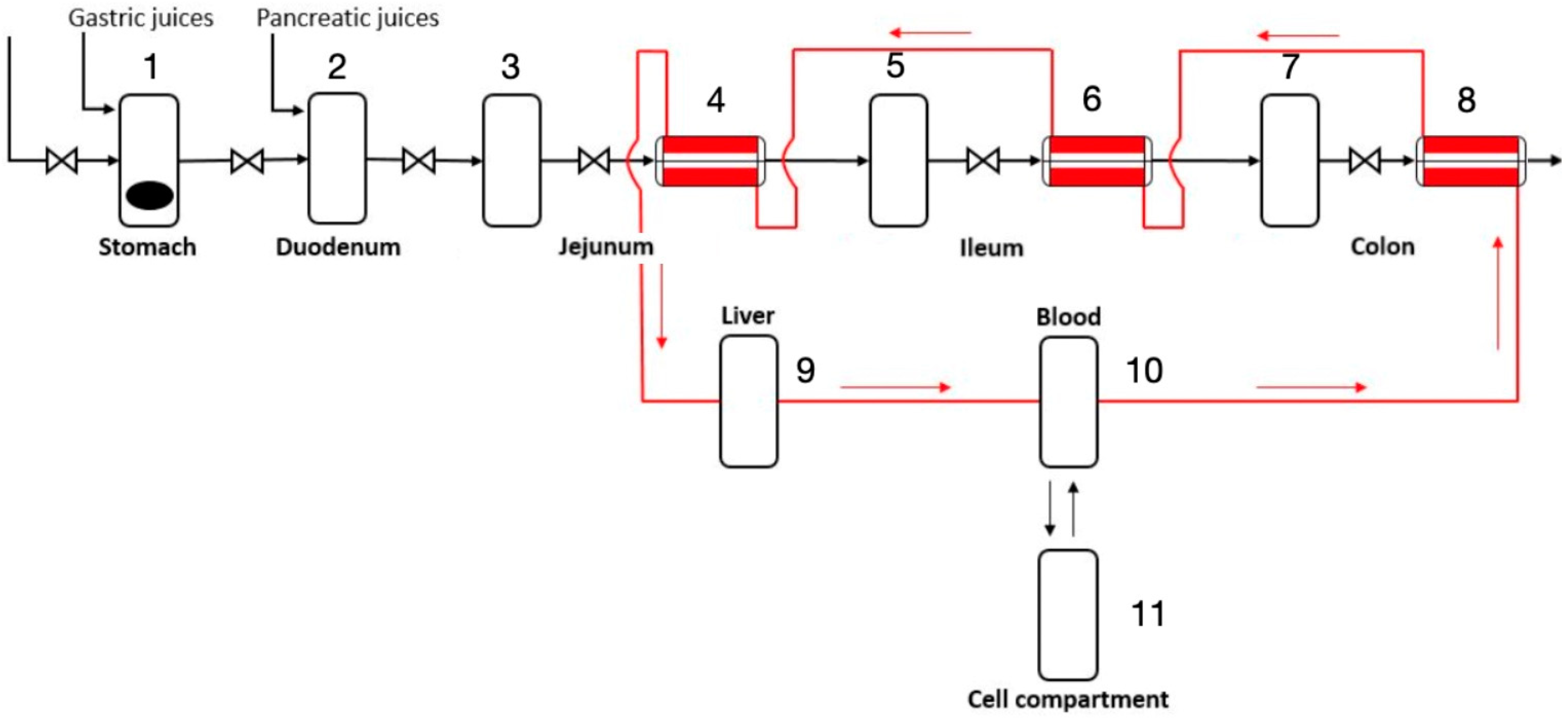
2.1. Stomach and Duodenum

Substances ingested orally first reach the stomach, which is responsible for the storage of the bolus and its initial cleavage by gastric juices. In the proposed model, this hollow organ is represented as a well-mixed compartment that receives as input the flow of food, the ingested drug, and the gastric juices secreted by its epithelial cells. Consequently, upon reaching the stomach, the bolus is subjected to the action of digestive acids and enzymes, including pepsin and gastric lipase, which initiate the process of degradation. Following partial digestion, the bolus, henceforth referred to as chyme, passes through the pyloric sphincter and is poured into the duodenum. The latter is again represented as a well-stirred compartment, in which the processing of the chyme occurs due to an additional flow of pancreatic juices and bile salts. The process of emptying follows the physiological dynamics of the stomach. At each step, a quantity equivalent to one-twentieth of the volume of the stomach is discharged into the intestine. Only when the duodenum finishes degrading it and empties it into the jejunum, the stomach releases another batch of bolus. It is therefore assumed that all nutrients are completely digested once they have passed through the duodenum. Both the stomach and duodenum are described by a set of ordinary differential equations (Equations (1)–(4)):

$${\displaystyle \frac{d{V}_i}{dt}}=Q_i-Q_{i+1}+Q_i^{juice}$$

(1)

$$V_i{\displaystyle \frac{d{N}_{i,j}}{dt}}+N_{i,j}{\displaystyle \frac{d{V}_i}{dt}}=Q_i{N}_{i-1,j}-{\displaystyle \frac{v_{i,j}^{max}{N}_{i,j}}{K_{i,j}^M+N_{i,j}}}{V}_i-k_{bd}{C}_i{V}_i$$

(2)

$$\epsilon \left(V_i{\displaystyle \frac{d{C}_i}{dt}}+C_i{\displaystyle \frac{d{V}_i}{dt}}\right)=Q_i{C}_{i-1}-Q_{i+1}{C}_i-\left(k_{bd}+k_{mic}\right)C_i{V}_i+k_i^d\left(S_i-C_i\right)$$

(3)

$$\left(1-\epsilon \right)\rho {\displaystyle \frac{d{r}_p}{dt}}=-k_i^d\left(S_i-C_i\right)$$

(4)

Equation (1) is the volume balance of the $\mathit{i}$-th compartment. ${\mathit{Q}}_{\mathit{i}}$ and ${\mathit{Q}}_{\mathit{i}}^{\mathit{j}\mathit{u}\mathit{i}\mathit{c}\mathit{e}}$ are, respectively, the flows of food and gastric/pancreatic juices entering the $\mathit{i}$-th compartment, whose volume is ${\mathit{V}}_{\mathit{i}}$. Equation (2) is the mass balance of the nutrients. Therefore, ${\mathit{N}}_{\mathit{i},\mathit{j}}$ denotes the concentration of nutrient $\mathit{j}$ in the $\mathit{i}$-th compartment, where the food and gastric juices are degraded according to the Michaelis–Menten kinetics (${\mathit{v}}_{\mathit{i},\mathit{j}}^{\mathit{m}\mathit{a}\mathit{x}}$ and ${\mathit{K}}_{\mathit{i},\mathit{j}}^{\mathit{M}}$) and a drug–bolus interaction constant (${\mathit{k}}_{\mathit{b}\mathit{d}}$). Equations (3) and (4) are the drug balances in the liquid and in the solid phase, respectively. ${\mathit{C}}_{\mathit{i}}$ denotes the drug concentration in the liquid phase in the $\mathit{i}$-th compartment, whereas ${\mathit{S}}_{\mathit{i}}$ is drug solubility in the solid phase, as described by the Noyes–Whitney equation [14]. The coefficient ${\mathit{k}}_{\mathit{m}\mathit{i}\mathit{c}}$ takes into account the effect of bile salt micelles on the solubility of the drug [15]. Finally, ${\mathit{r}}_{\mathit{p}}$ and $\mathit{\rho }$ are the drug tablet’s radius and density; $\mathit{\epsilon }$ is the liquid fraction, and ${\mathit{k}}_{\mathit{i}}^{\mathit{d}}$ is the mass transfer coefficient between the two phases.

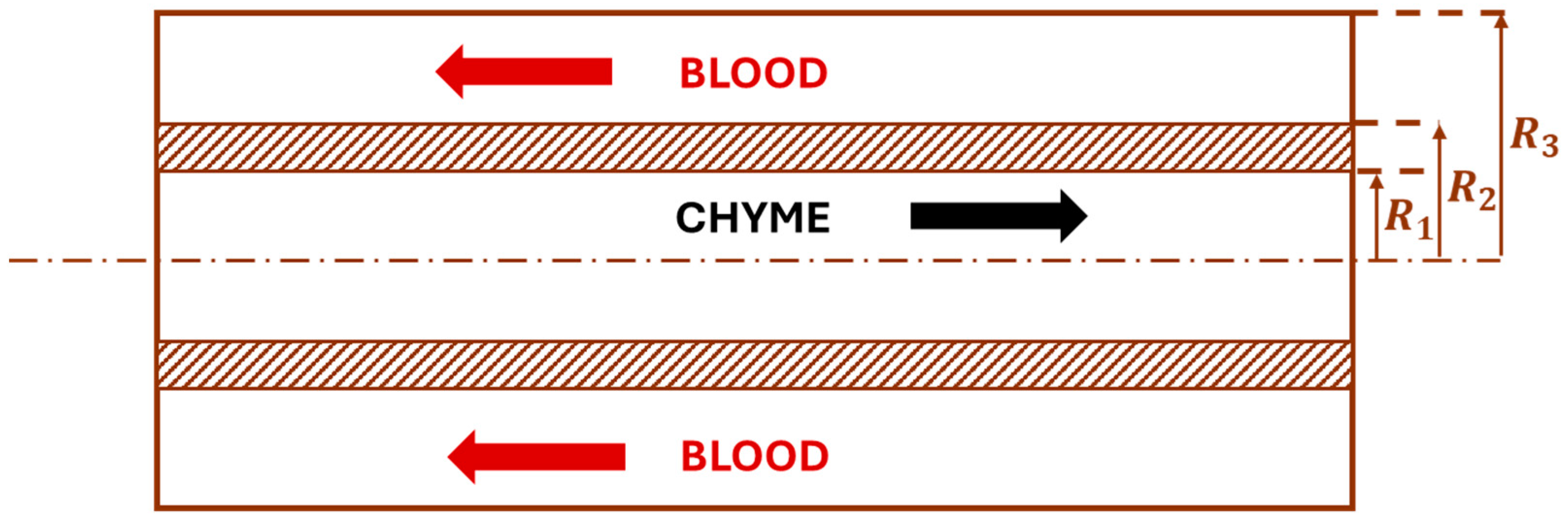
2.2. Jejunum, Ileum, and Colon

The jejunum, ileum, and colon are modeled as a series of a well-stirred compartment and a hollow fiber reactor. The latter is formed by two concentric cylinders: the inner one represents the intestinal lumen, in which the chyme moves, whereas the blood flows in the outer cylinder, in the opposite direction, as schematically depicted in Figure 2. This representation of the intestine introduces a spatiotemporal dependence for the drug concentration, as illustrated in Equations (5) and (6):

$${\displaystyle \frac{d{C}_i^l}{dt}}=-v_i^l{\displaystyle \frac{d{C}_i^l}{dz}}-{\displaystyle \frac{2P_i{\alpha }_i\left(C_i^l-C_i^s\right)}{R_{i1}}}-{\displaystyle \frac{v_i^m{C}_i^l}{k_i+C_i^l}}$$

(5)

$${\displaystyle \frac{d{C}_i^s}{dt}}=-v_i^s{\displaystyle \frac{d{C}_i^s}{dz}}+{\displaystyle \frac{2P_i{R}_{i2}{\alpha }_i\left(C_i^l-C_i^s\right)}{R_{i3}^2-R_{i2}^2}}+{\displaystyle \frac{v_i^m{C}_i^l}{k_i+C_i^l}}$$

(6)

where the superscripts $\mathit{l}$ and $\mathit{s}$ refer to the lumen and the shell, respectively, while the subscript $\mathit{i}$ indicates the $\mathit{i}$-th compartment. ${\mathit{P}}_{\mathit{i}}$ denotes the permeability of the intestinal membrane, whereas ${\mathit{\alpha }}_{\mathit{i}}$ is an amplification factor, introduced to take into account the different absorption capabilities of each tract [4]. Finally, given that the drug present in the intestinal lumen can reach the blood fluid by passing through the intestinal membrane via active transport, the Michaelis–Menten kinetics (${\mathit{v}}_{\mathit{i}}^{\mathit{m}}$ and ${\mathit{k}}_{\mathit{i}}$) was introduced to account for this phenomenon.

2.3. Cardiovascular System

In addition to the flow in the outer cylinders of the hollow fiber reactors of the jejunum, ileum, and colon, the blood enters and leaves a well-stirred compartment representing the vascular circulation. The latter communicates with a cellular compartment (extravascular circulation) and the liver (responsible for the first-pass effect [16]), both modeled as CSTRs, as described in Equations (7)–(9):

$$V_9{\displaystyle \frac{d{C}_9}{dt}}=Q_9\left(C_4^s-C_9\right)-{\displaystyle \frac{v_9^m{C}_9}{k_9+C_9}}$$

(7)

$$V_{10}{\displaystyle \frac{d{C}_{10}}{dt}}=Q_{10}\left(C_9-C_{10}\right)+Q_{11}\left(C_{11}-C_{10}\right)-K_B{C}_{10}$$

(8)

$$V_{11}{\displaystyle \frac{d{C}_{11}}{dt}}=Q_{11}\left(C_{10}-C_{11}\right)-K_P{C}_{11}$$

(9)

The subscripts 9, 10, and 11 refer to the liver, blood, and cellular compartments, respectively. The first-pass effect of the liver is modeled through the Michaelis–Menten kinetics, while the drug removal rate in both the blood and cellular compartments is described by first-order kinetics (${\mathit{K}}_{\mathit{B}}$ and ${\mathit{K}}_{\mathit{P}}$).

2.4. Parameters Estimation

Despite its complexity, the model is characterized by only 5 parameters: the permeability constant of the jejunum (${\mathit{P}}_4$), ileum (${\mathit{P}}_6$), and colon (${\mathit{P}}_8$) membranes and the drug removal rate in the blood (${\mathit{K}}_{\mathit{B}}$) and in the cellular compartment (${\mathit{K}}_{\mathit{P}}$). By defining the parameter vector $\mathit{\theta }=\left[{\mathit{P}}_4,{\mathit{P}}_6,{\mathit{P}}_8,{\mathit{K}}_{\mathit{B}},{\mathit{K}}_{\mathit{P}}\right]$, the parameter estimation is achieved by minimizing the ${\mathit{L}}_2$ square norm of the sum of the trajectory errors for each active pharmaceutical ingredient (API) (Equation (10)):

$${\mathit{\theta }}^{\mathit{*}}=\underset{\mathit{\theta }}{\mathbf{min}}{\int }_0^{\mathit{T}}\left({\left|{\mathit{C}}_{\mathit{F}}^{\widehat{\mathit{\theta }}}\left(\mathit{t}\right)-{\mathit{C}}_{\mathit{F}}\left(\mathit{t}\right)\right|}^2+{\left|{\mathit{C}}_{\mathit{N}}^{\widehat{\mathit{\theta }}}\left(\mathit{t}\right)-{\mathit{C}}_{\mathit{N}}\left(\mathit{t}\right)\right|}^2\right)\mathit{d}\mathit{t}$$

(10)

$\mathit{C}$ is the measured drug concentration in the blood, as derived from the literature, whereas ${\mathit{C}}^{\widehat{\mathit{\theta }}}$ is the value of the drug concentration in the blood compartment, evaluated using the model. The subscripts $\mathit{F}$ and $\mathit{N}$ denote the presence or absence of food, respectively. As a whole, the model is tested on two different APIs, Ketoprofen (belonging to the family of anti-inflammatory and anti-rheumatic drugs) [17] and Ibuprofen (belonging to the family of non-steroidal drugs with analgesic, anti-inflammatory, and anti-pyretic properties) [18]. For each test, the values of physio-anatomical parameters are retrieved from the literature [10,11,15], whereas the data related to APIs are extrapolated from the drug bank [12].

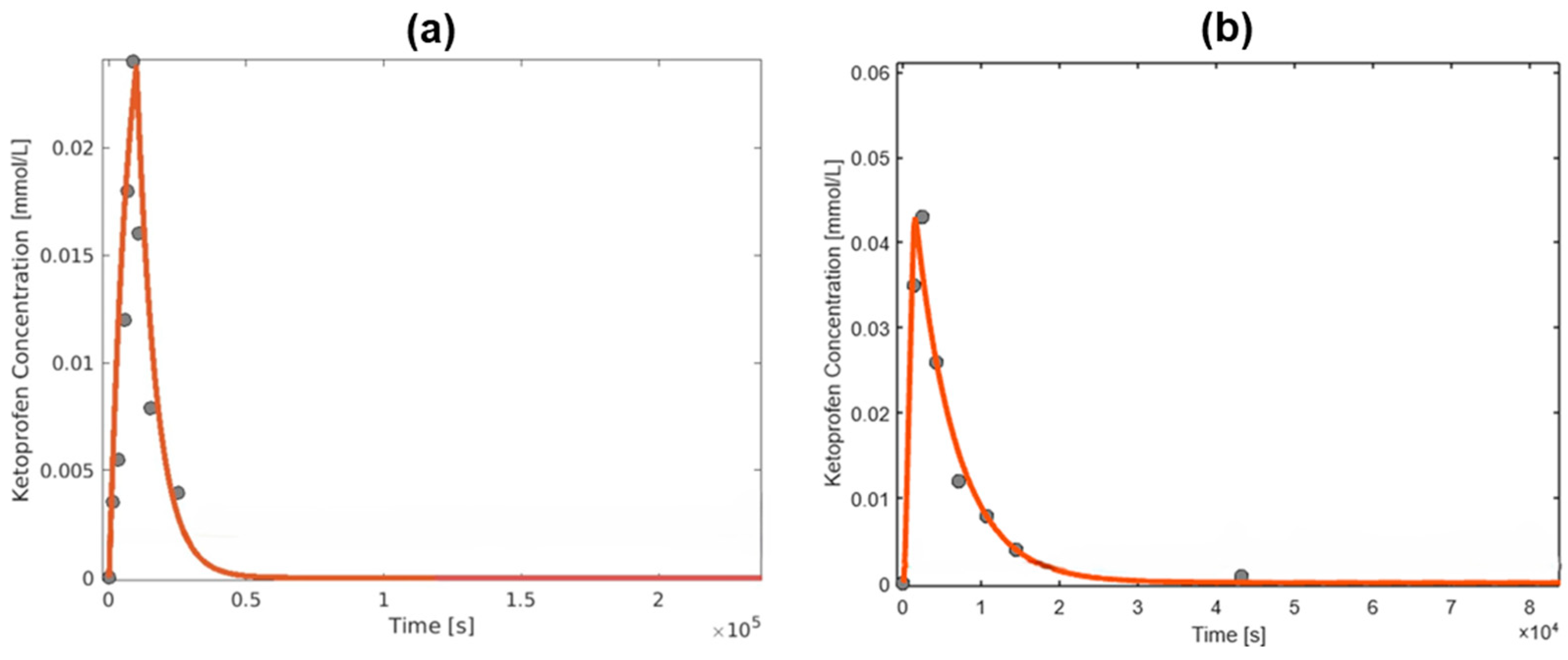
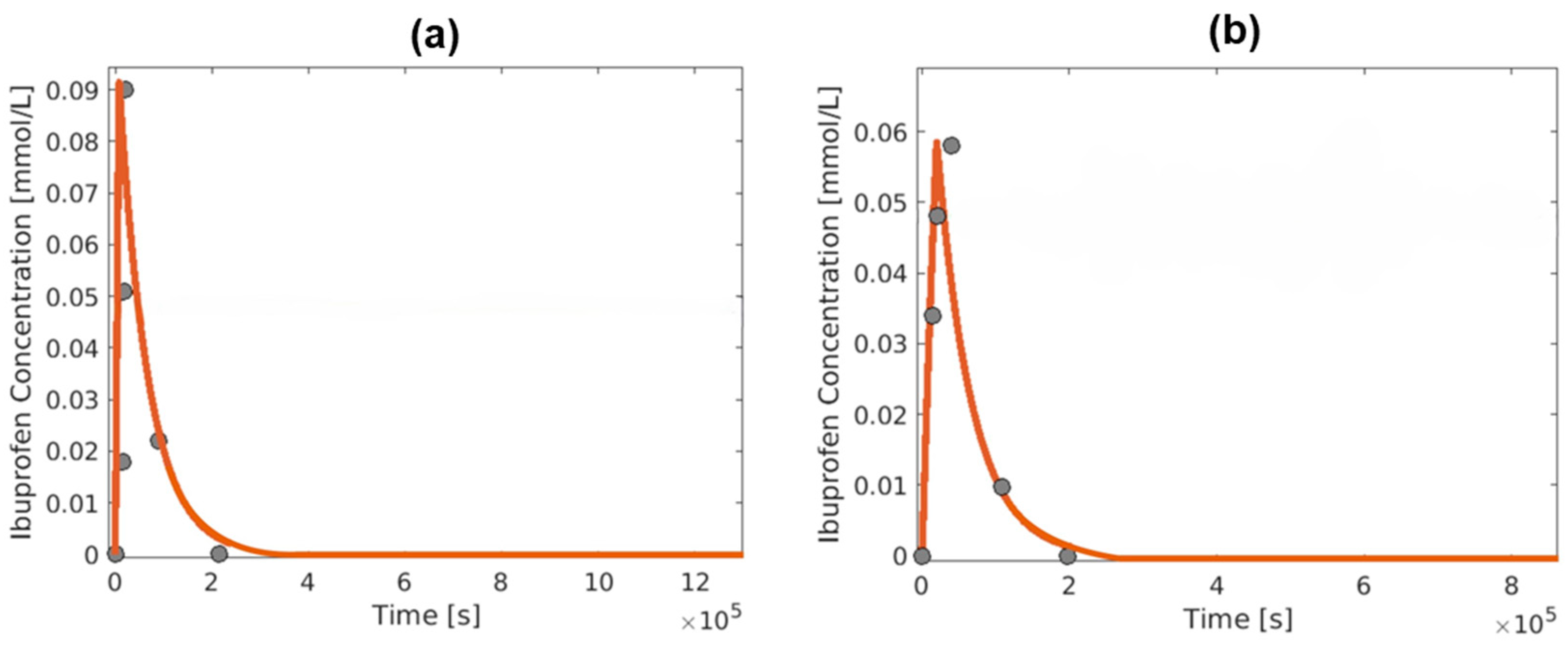
3. Results and Discussion

Figure 3 and

Table 1. Results of parameter estimation for Ketoprofen.

Parameter	Value
$P_4\left[\mathrm{c}\mathrm{m} {\mathrm{s}}^{-1}\right]$	$1.0\cdot {10}^{-4}$
$P_6\left[\mathrm{c}\mathrm{m} {\mathrm{s}}^{-1}\right]$	$6.2\cdot {10}^{-3}$
$P_8\left[\mathrm{c}\mathrm{m} {\mathrm{s}}^{-1}\right]$	$6.3\cdot {10}^{-3}$
$K_B\left[{\mathrm{s}}^{-1}\right]$	$0.57$
$K_P\left[{\mathrm{s}}^{-1}\right]$	$1.2$

illustrate the results of the model simulation for Ketoprofen.

Similarly, Figure 4 and

Table 2. Results of parameter estimation for Ibuprofen.

Parameter	Value
$P_4\left[\mathrm{c}\mathrm{m} {\mathrm{s}}^{-1}\right]$	$4.4\cdot {10}^{-4}$
$P_6\left[\mathrm{c}\mathrm{m} {\mathrm{s}}^{-1}\right]$	$5.5\cdot {10}^{-3}$
$P_8\left[\mathrm{c}\mathrm{m} {\mathrm{s}}^{-1}\right]$	$5.0\cdot {10}^{-3}$
$K_B\left[{\mathrm{s}}^{-1}\right]$	$0.18$
$K_P\left[{\mathrm{s}}^{-1}\right]$	$1.9$

show the results of the model simulation for Ibuprofen.

In general, there is a good agreement between the concentrations predicted by the model and the experimental data. The primary discrepancies, when present, are mainly observed at the time of the maximum concentration in the absence of food.

It is crucial to note that there are already several advanced models that incorporate multiple biological and biochemical factors to capture the complex mechanisms governing drug absorption in the gut [19,20]. While these models provide valuable insights into the inter-individual variability and influence of physiological conditions, they are often characterized by a high computational burden and require a large number of parameters, which may be difficult to determine experimentally with sufficient accuracy and reliability [10]. In contrast, the proposed model offers a computationally efficient alternative that balances simplicity and predictive capability. Unlike more intricate frameworks, it does not require extensive parameterization or detailed physiological compartmentalization, making it more practical in early-stage drug testing, where experimental data are often scarce. Furthermore, its generalizability allows for applications beyond a specific drug class. As long as the necessary parameters are available and no “atypical absorption phenomena” (e.g., nonlinear transport mechanisms or precipitation effects) occur, the model can be readily adapted to other drugs in tablet formulations. By offering a rapid, preliminary estimation of key pharmacokinetic parameters, the model can serve as an effective screening tool before transitioning to more complex and computationally demanding simulations.

4. Conclusions

In this study, a PBPK model of the gastrointestinal system, comprising 11 compartments, was developed to simulate drug transport, distribution, and absorption. The model is defined by only five parameters and exhibits a low computational burden. Consequently, it may be employed in preliminary drug bioavailability assessments, which are conducted during the initial stages of drug development when experimental data are scarce.

However, the quality and quantity of input data are directly correlated with the overall efficacy of the model. Therefore, the model should be validated on a broader set of drugs. In light of these considerations, future research directions include the following:

• Assessing and validating the model over a larger set of data, comprising a greater number of drugs.
• Comparing the model with previous works in terms of both computational burden and accuracy.
• Considering the possibility of incomplete solubilization of the drug and of enterohepatic circulation.