Abstract
In certain applications of acoustic emission sensors, acoustic maps can be generated from captured signals. The work “In-Dressing Acoustic Map by Low-Cost Piezoelectric Transducer” introduces an innovative technique using these sensors to map grinding wheel surfaces, essential for finishing machined parts. However, producing sharp acoustic maps is challenging due to industrial interference. This study explores digital image processing techniques to enhance these maps, using cloud-based tools. Techniques such as smoothing, equalization, and edge detection (Sobel, Canny, Roberts, and Prewitt) were applied. The processed acoustic maps revealed sharper details, enabling more accurate assessments of dressing conditions. The results demonstrate the effectiveness of digital image processing when applied to acoustic maps, significantly improving the evaluation of the dressing process and contributing to the development of Industry 4.0.
1. Introduction
As described in [1], grinding is a material removal process carried out using an abrasive tool, the grinding wheel, which is a disk-shaped component composed of high-hardness grains that rotates around its own axis. In summary, it is a rotary abrasive tool widely used to provide final finishing to previously machined parts.
According to [2], over time, the surface of the grinding wheel tends to wear down and become glazed, when the pores of the wheel get clogged with chips, impairing the grinding process. To restore the grinding wheel’s surface and ensure optimal grinding performance, a process called dressing is required, in which the abrasive wheel is machined, balanced, and its surface renewed, restoring its abrasive properties.
Monitoring the dressing process of the grinding wheel is crucial to ensure the quality of the grinding and, consequently, the surface finish of the parts. Several studies have been conducted to monitor the grinding wheel using sensors to determine the optimal time for dressing [3,4]. The work of In-Dressing Acoustic Map by Low-Cost Piezoelectric Transducer [5], in particular, addresses the surface mapping of grinding wheels in the dressing process, using certain acoustic emission sensors.
However, in the generated acoustic maps, noise with tonalities close to the known figures can be observed, a characteristic that can hinder and invalidate processing using simple filtering methods. It is also observed that the known images are illustrated by abrupt variations in gray tones in certain regions. This characteristic fits the definition of edges, and thus the possibility of applying edge detection algorithms, such as the Sobel Filter, Prewitt, Roberts, and Canny algorithm, is questioned.
Thus, this study proposes the application of edge detection algorithms, such as Sobel, Prewitt, Roberts, and Canny, to enhance the interpretation of acoustic maps generated during the dressing process. By using these tools, it is expected to enhance the identification of defects and marks on the grinding wheel’s surface, minimizing noise interference that could compromise the accuracy of the analyses. This work aims to contribute to the development of more robust monitoring methods capable of ensuring a more precise and effective evaluation of the state of the grinding wheels, optimizing the grinding process and, consequently, the quality of the machined parts.
2. Methodology
Figure 1 illustrates one of the acoustic maps obtained in [5]. In this study, the authors performed the dressing of a grinding wheel with known symbols engraved on it. During the restoration process, acoustic signals were captured by sensors strategically placed on the tool, enabling the generation of a topological map, as shown.

Figure 1.
Original acoustic map of the marks inserted on the grinding wheel: (a) “+” mark; (b) “T” mark [5].
These acoustic maps are essentially grayscale images, where significant details are indicated by abrupt variations in intensity. However, the nature of the collected signals introduces a considerable amount of noise, resulting in polluted acoustic maps that distort, attenuate, and even obscure the tonal variations crucial for identifying the regions of interest. It is important to note that the acoustic map presented in the figure already employs certain filters in an attempt to make the details more visible; however, as can be seen, these filters were not sufficient to significantly reduce the noise.
The following sections present and discuss the operation of advanced digital image processing tools. These tools have the potential to enhance details in noise-polluted images, surpassing the currently applied methods and improving the visual interpretation of acoustic maps.
2.1. Edge Detection
The visual analysis of the generated acoustic map confirms the ineffectiveness of using basic filters, highlighting the need for more advanced image processing tools, such as edge detection techniques. In this work, edge detection is performed by applying masks (kernels) to the image using the convolution procedure, which allows for identifying abrupt changes in intensity and facilitating a more precise analysis of the acoustic map characteristics.
The convolution process in image processing, as discussed by Gonzales [6], involves applying the kernel to each pixel of an image sequentially. This filter analyzes each pixel, known as the “initial pixel,” along with its neighbors if the image is two-dimensional. For each of these pixels, the values are multiplied by the corresponding values in the kernel, and the sum of these products becomes the new value of the initial pixel. This process is repeated for all the pixels in the image, thereby affecting each pixel based on the values of its neighbors.
To illustrate, consider the following array to which we will apply the mask:
And we have the following mask:
To perform the convolution A ∗ K, we center the mask on the first pixel of the array and calculate the sum of the products of the corresponding elements. For example, for the first pixel, the calculation is as follows:
The result of this calculation will then be the first value of the final matrix. To continue with the convolution, we repeat the same process, shifting the mask from right to left and from top to bottom.
After performing all the necessary calculations, the resulting matrix from the convolution will be as follows:
As mentioned earlier, what differentiates the Roberts, Prewitt, and Sobel edge filters are the masks, which have distinct dimensions and values. The following sections present each edge detector, showing the kernel to be convolved and highlighting the characteristics of each method.
2.2. Sobel, Prewitt, Roberts, and Canny Detectors
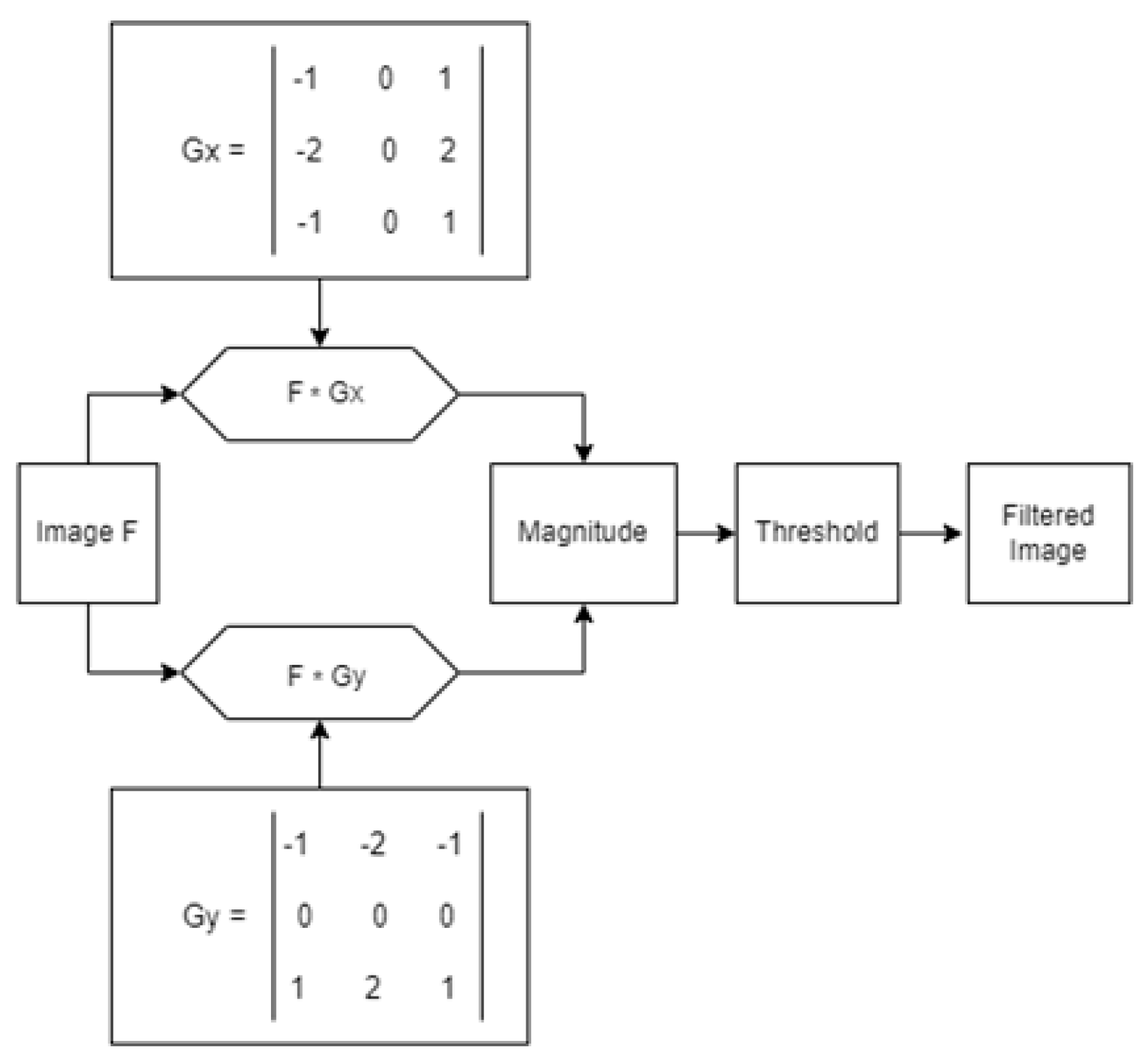
According to Rakesh Ranjan and Vinay Avasthi [7], the Sobel operator is one of the most commonly used for edge detection. It evaluates the gradient of intensity at each pixel and provides information about the direction (x and y) and magnitude of the maximum gradient. To perform edge detection using the Sobel operator, two kernels are used: one for the x direction and another for the y direction, as shown in Equations (5) and (6).
The diagram in Figure 2 represents the functioning of the Sobel edge detector. First, the Sobel masks (Gx and Gy) are convolved with the image to evaluate the gradient of the image in the X and Y directions. These results can then be combined to find the absolute magnitude of the gradient at each point and the orientation of this gradient. Once the gradient is obtained, an appropriate threshold is selected to distinguish between edge pixels and non-edge pixels. This thresholding step is responsible for identifying and detecting the presence and orientation of edges in the image.
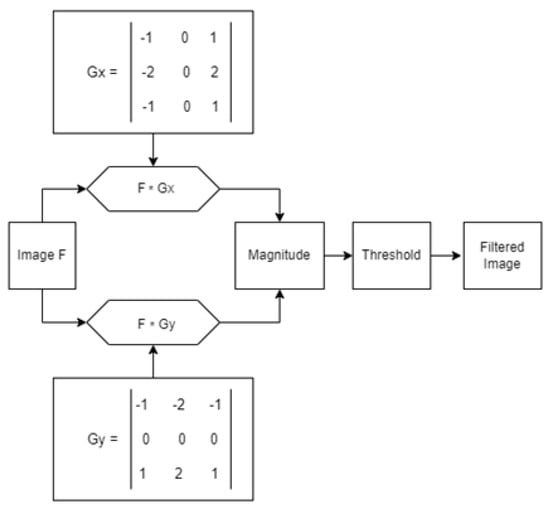
Figure 2.
Sobel application diagram.
The gradient magnitude G is calculated as the square root of the sum of the squares of the gradients in the x and y directions, as shown in the figure below.
Due to the greater weight at the edges of the mask, the Sobel edge detection method places more emphasis on pixels that are in the direction of the gradient, with a characteristic of slightly smoothing some noise. Compared to more advanced algorithms, it has the disadvantage of potentially rejecting real edges, where some edges may not be accurately detected. Additionally, the Sobel operator is sensitive to noise, which can lead to the detection of false edges in the presence of noise. These limitations should be considered when using this method in practical applications.
Prewitt also uses two kernels, Gx and Gy, to search in the horizontal and vertical directions. The shapes of the kernels Gx and Gy are illustrated in Equations (8) and (9) [8].
The Prewitt method is very similar to the Sobel method, both in the dimensions of the kernel and in the application, following the diagram in Figure 2. The difference lies in the weights of some coefficients at the edges of the masks [9]. This difference at the edges of the kernels gives the Prewitt method a greater sensitivity to thin edges, as it eliminates the smoothing characteristic but is more susceptible to noise and false edge detections.
The Roberts detector, on the other hand, is defined by two matrices (masks) but with 2 × 2 dimensions, having the characteristic of being simpler and faster to compute. However, it is not as widely used as other edge detectors due to its asymmetry. The matrices of the Roberts detector (Roberts operator) are defined by Equations (10) and (11). This format gives the method the characteristic of diagonal filtering, being the simplest of all.
The calculation of the gradient components Gx and Gy is performed in the same way as for the Sobel and Prewitt detectors, i.e., by 2D convolution of the Roberts operator with the image, gradient magnitude calculation through the combination of gradients, and thresholding [10].
Compared to the methods discussed up to the previous section, the Canny algorithm is of higher complexity. Unlike simple binary maps, the Canny algorithm achieves high-performance edge detection, ensuring an appropriate edge width. The Canny algorithm can be divided into four different stages:
- Gaussian filtering;
- Gradient magnitude calculation;
- Non-maximum suppression;
- Edge tracking by hysteresis.
First, the input image is smoothed using a Gaussian filter. Then, the edge gradient is calculated similarly to the Sobel operator. In the non-maximum suppression step, the gradient at each edge point is compared, eliminating those that do not represent the local maximum. Finally, in the edge tracking by hysteresis step, edges connected to strong edge pixels are identified, ensuring a more precise and continuous detection of edges [11]. However, it can be stated that the Canny algorithm is insensitive to slightly smooth edges, as the Gaussian smoothing performed at the beginning of the algorithm tends to consider small variations such as noise [12].
2.3. Edge Detection in the Cloud
In the development of this study, the choice of Google Colab as the platform for performing filtering and image processing is motivated by several factors. Firstly, Google Colab is a free tool that supports the use of popular data science and machine learning libraries, as well as providing cloud processing infrastructure. This enables the study to be conducted efficiently without the need for advanced local computational resources.
Additionally, using Google Colab provides access to libraries that already include the essential features for executing the discussed algorithms. Libraries such as cv2, which is part of OpenCV, can be extensively used in this study to apply the Sobel, Prewitt, Roberts, and Canny methods, streamlining the development and analysis process. The use of pre-compiled and optimized libraries allows for the efficient application of these algorithms, which is crucial for real-time data analysis, such as with acoustic emission sensors.
Among the libraries used, numpy and matplotlib stand out, employed for mathematical operations and signal processing. Numpy is used for vector calculations and matrix manipulation, essential elements for handling acoustic data and processed images. Matplotlib is utilized for a graphical visualization of the results, allowing for a clear and objective analysis of the edges detected by each algorithm. These libraries, combined with the processing framework of Google Colab, ensure the smooth flow of this study, from data acquisition to the final visualization of images.
3. Results and Discussion
The analysis of the results was conducted by examining the characteristics of the final images obtained after applying each proposed method. This analysis details the aspects of each image concerning the specific characteristics of each filter and compares the effectiveness of the methods with each other. The following figures show the resulting images from each method discussed in the previous section.
Comparing the Figure 3 and Figure 4, there is a minimal difference between the results of the Prewitt and Sobel filters, where the image filtered by Prewitt shows a subtle enhancement of certain details in some regions, due to the similarity between their kernels, as described in previous sections. Compared to the Figure 5, it is observed that Roberts identifies slightly smoother edges with less contrast. Due to the shape of the Roberts kernel, this method ends up presenting some intended details, although these are in lower contrast, making it simple to apply another filtering method to eliminate them.

Figure 3.
Image with Sobel detector: (a) “+” mark; (b) “T” mark.

Figure 4.
Image with Prewitt detector: (a) “+” mark; (b) “T” mark.

Figure 5.
Image with Roberts detector: (a) “+” mark; (b) “T” mark.
Canny, shown in Figure 6, stands out for its efficient noise filtering, its ability to reject unwanted edges, and the greater thickness of the lines marking the edges. However, it is noted that the detection of known edges can be impaired due to the large number of procedures involved. Although the Canny algorithm is effective in identifying edges, it may, in some cases, distort the actual contours of the image, resulting in a less accurate representation.

Figure 6.
Image with Canny detector: (a) “+” mark; (b) “T” mark.
To benefit the analysis by utilizing the particularities of each edge detector, the possibility of overlaying filtered images is highlighted. That is, by overlaying two images, each processed with different edge detection methods, a more comprehensive analysis of the acoustic map can be achieved. The Figure 7 places the image filtered with the Sobel method at 50% transparency over the edges identified by Canny.

Figure 7.
Canny image with 50% Sobel overlay: (a) “+” mark; (b) “T” mark.
This analysis allows for the visualization of details omitted or distorted by the Canny method, providing a more flexible visual analysis of the final image. Since the intensity of edge indications from the methods may be similar, it is necessary to apply a transparency index in the overlay so that the secondary image does not compromise the integrity of the primary method. This approach allows for a complete and flexible analysis of the surface of the grinding wheel, minimizing unwanted signals, false edge detections, and amplifying key details.
4. Conclusions
This study demonstrated that the application of image processing techniques, especially edge detection algorithms, offers an effective method for improving the visualization of acoustic maps in abrasive wheel dressing processes. The use of Google Colab for cloud processing was particularly advantageous, as it provided a robust and accessible infrastructure for executing complex algorithms without the need for advanced local computational resources. This aligns with the principles of Cloud Manufacturing, where cloud-based platforms facilitate scalable, flexible, and efficient manufacturing processes. The platform also facilitated the integration of libraries such as cv2, numpy, and matplotlib, allowing for an efficient workflow and detailed data analysis. The overlay of different algorithms, such as Sobel and Canny, enabled a more detailed and flexible analysis of the detected edges, highlighting important characteristics for monitoring and controlling tool wear. The results suggest that using these tools can not only contribute to improving the quality of acoustic maps but also facilitate the integration of these image processing methods into TCM systems for monitoring the dressing process, indirectly optimizing grinding, improving the quality of machined parts, and ensuring greater efficiency in controlling the wheel’s condition. Additionally, the discussed approaches can be expanded to other machining processes, such as turning and milling, contributing to the advancement of sensor-based monitoring technologies and supporting the development of Industry 4.0, where modern technology-based solutions are fundamental for smart manufacturing systems.
Author Contributions
Conceptualization, F.R.L.D. and P.R.d.A.; methodology, M.L.D. and M.R.B.; software, M.L.D. and M.R.B.; validation, F.R.L.D., P.d.O.C.J. and P.R.d.A.; formal analysis, F.R.L.D.; investigation, M.L.D.; resources, M.L.D.; data curation, F.R.L.D.; writing—original draft preparation, M.L.D.; writing—review and editing, M.L.D. and F.R.L.D.; visualization, M.R.B., P.R.d.A. and P.d.O.C.J.; supervision, F.R.L.D.; project administration, F.R.L.D.; funding acquisition, F.R.L.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Pro-Rectory of Research and Innovation of the University of São Paulo under grant: #22.1.09345.01.2, and the São Paulo Research Foundation, under grant #2024/01374-6.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Dataset available on request from the authors.
Acknowledgments
The authors would like to thank the University of São Paulo (USP) and the São Paulo State University (UNESP) for the opportunity to carry out and publish this research.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Schwendemann, S.; Amjad, Z.; Sikora, A. A survey of machine-learning techniques for condition monitoring and predictive maintenance of bearings in grinding machines. Comput. Ind. 2021, 125, 17. [Google Scholar] [CrossRef]
- Marinescu, I.D.; Hitchiner, M.P.; Uhlmann, E.; Rowe, W.B.; Inasaki, I. Griding of Ceramics. In Handbook of Machining with Grinding Wheels, 1st ed.; Boothroyd, G., Ed.; CRC Press: Boca Raton, FL, USA, 2006; Volume 1, pp. 267–283. [Google Scholar]
- Ruas, E.L.V.; Lopes, W.N.; de Aguiar, P.R.; Lopes, T.G.; Conceição Junior, P.O. Monitoring the dressing operation of conventional aluminum oxide grinding wheels through damage index, power spectral density, and piezoelectric sensors. Int. J. Adv. Manuf. Technol. 2023, 127, 2759–2773. [Google Scholar] [CrossRef]
- Wegener, K.; Hoffmeister, H.-W.; Karpuschewski, B.; Kuster, F.; Hahmann, W.-C.; Rabiey, M. Conditioning and monitoring of grinding wheels. CIRP Ann. Manuf. Technol. 2011, 60, 757–777. [Google Scholar] [CrossRef]
- Dotto, F.R.L.; Aguiar, P.R.; Alexandre, F.A.; Lopes, W.N.; Bianchi, E.C. In-Dressing Acoustic Map by Low-Cost Piezoelectric Transducer. IEEE Trans. Ind. Electron. 2020, 67, 6927–6936. [Google Scholar] [CrossRef]
- Gonzales, R.C.; Woods, R.E. Digital Image Processing, 4th ed.; Pearson Education Limited: Upper Saddle River, NJ, USA, 2017; pp. 154–162. [Google Scholar]
- Ranjan, R.; Avasthi, V. Edge Detection Using Guided Sobel Image Filtering. Wireless Pers. Commun. 2023, 132, 651–677. [Google Scholar] [CrossRef]
- Rahman, A.Y.; Zakaria, Z. Schematic Edge Detection of Power Distribution Networks Using the Canny, Sobel, Robert, and Prewitt Algorithms. In Proceedings of the IEEE International Conference on Computing (ICOCO), Langkawi, Malaysia, 9–12 October 2023; Volume 1, pp. 391–396. [Google Scholar]
- Yadav, J.S.; Shyamala Bharathi, P. Edge Detection of Images Using Prewitt Algorithm Comparing with Sobel Algorithm to Improve Accuracy. In Proceedings of the International Conference on Intelligent Engineering and Management (ICIEM), London, UK, 27–29 April 2022; pp. 351–355. [Google Scholar]
- Ladányi, L.; Králik, M. Automatic Buildings Detection Using Sobel, Roberts, Canny, and Prewitt Detectors. J. Electr. Eng. 2021, 72, 278–282. [Google Scholar]
- Kwon, Y.H.; Jeon, J.W. Comparison of FPGA Implemented Sobel Edge Detector and Canny Edge Detector. In Proceedings of the 2020 IEEE International Conference on Consumer Electronics—Asia (ICCE-Asia), Seoul, Republic of Korea, 1–3 November 2020; Volume 1, pp. 1–2. [Google Scholar]
- Rahman, M.A.; Amin, M.F.I.; Hamada, M. Edge Detection Technique by Histogram Processing with Canny Edge Detector. In Proceedings of the IEEE International Conference on Knowledge Innovation and Invention (ICKII), Kaohsiung, Taiwan, 21–23 August 2020; Volume 1, pp. 128–131. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).