Development and Implementation of Modular Turning Dynamometer with Miniature Load Cell †
Abstract
:1. Introduction
2. Materials and Methods
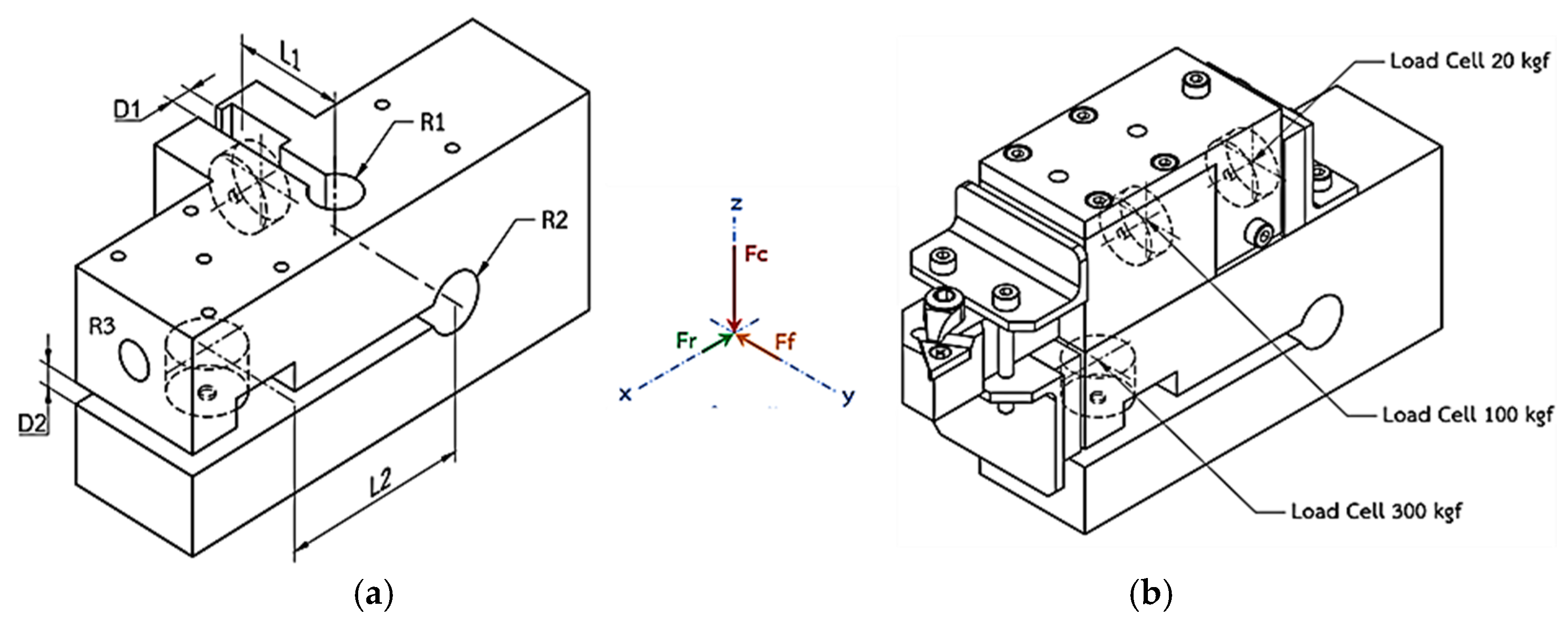
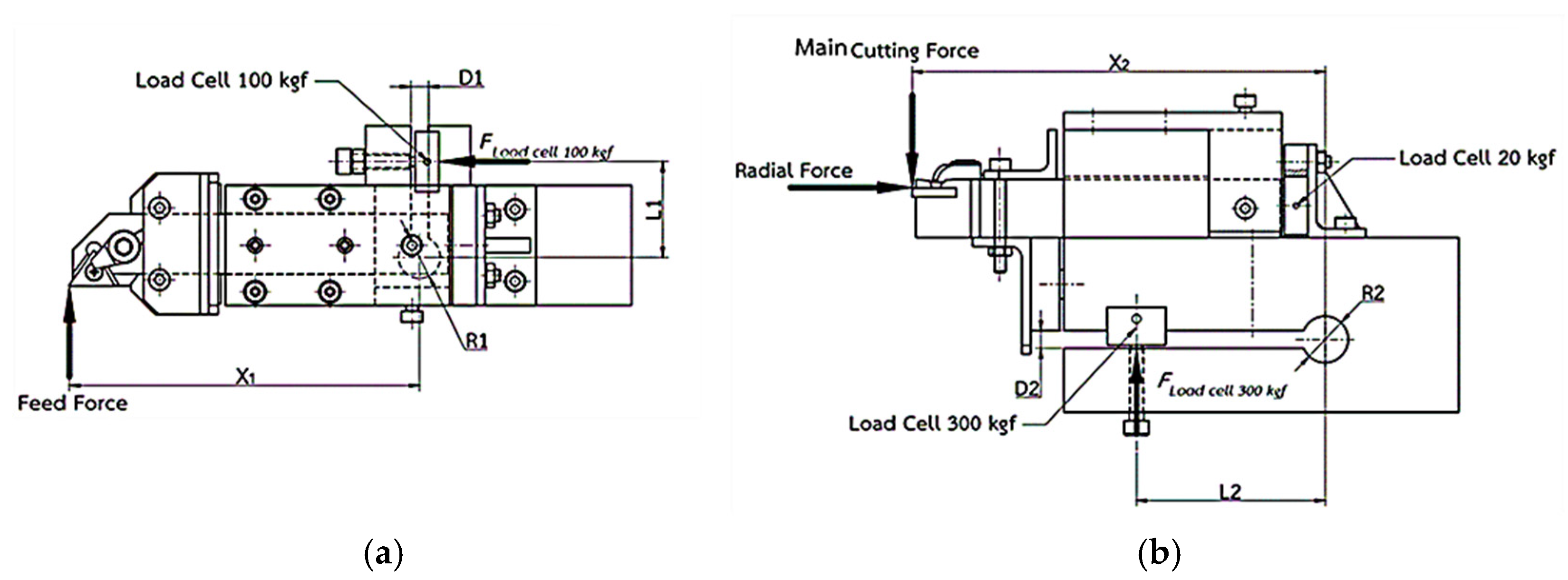
2.1. Main Concept for Modular Turning Dynamometer Design
2.2. Finite Element Analysis for Dynamometer Parameter Optimization
2.3. Measuring System Configuration and Display Software
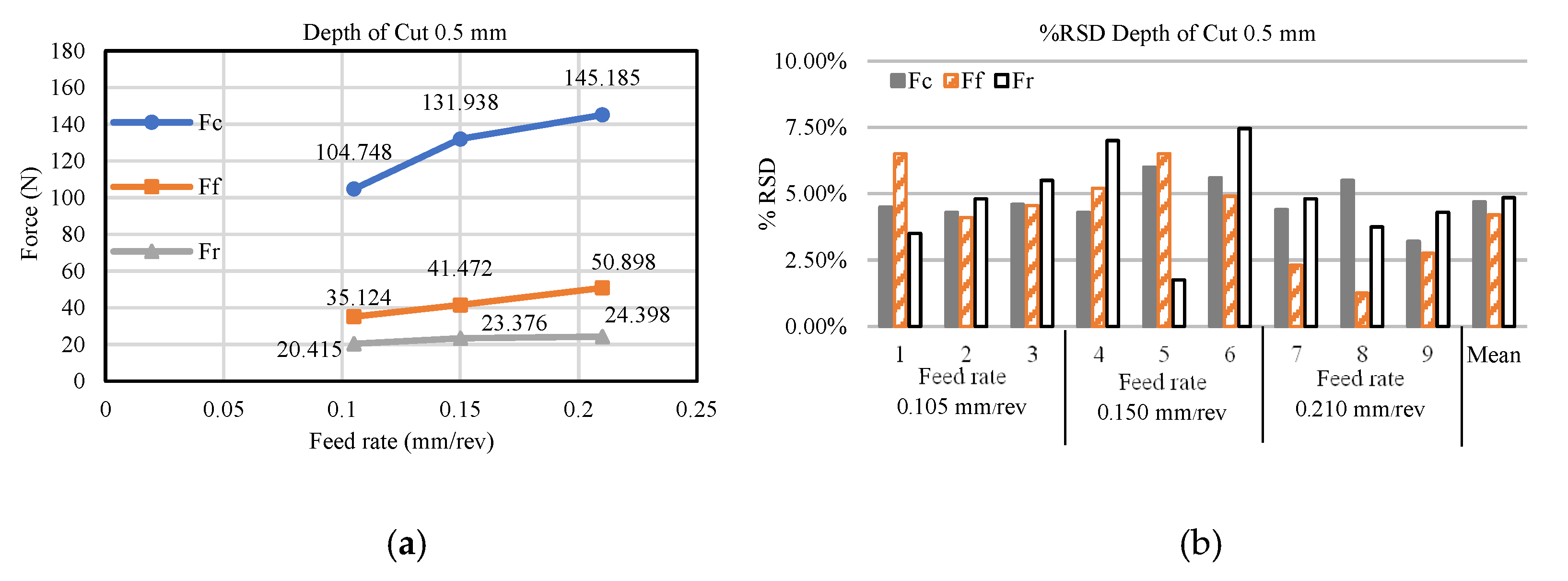
2.4. Experimentation and Precision Analysis
3. Design and Implementation Results
3.1. Dynamometer Parameter Optimization
3.2. Modular Turning Dynamometer Design
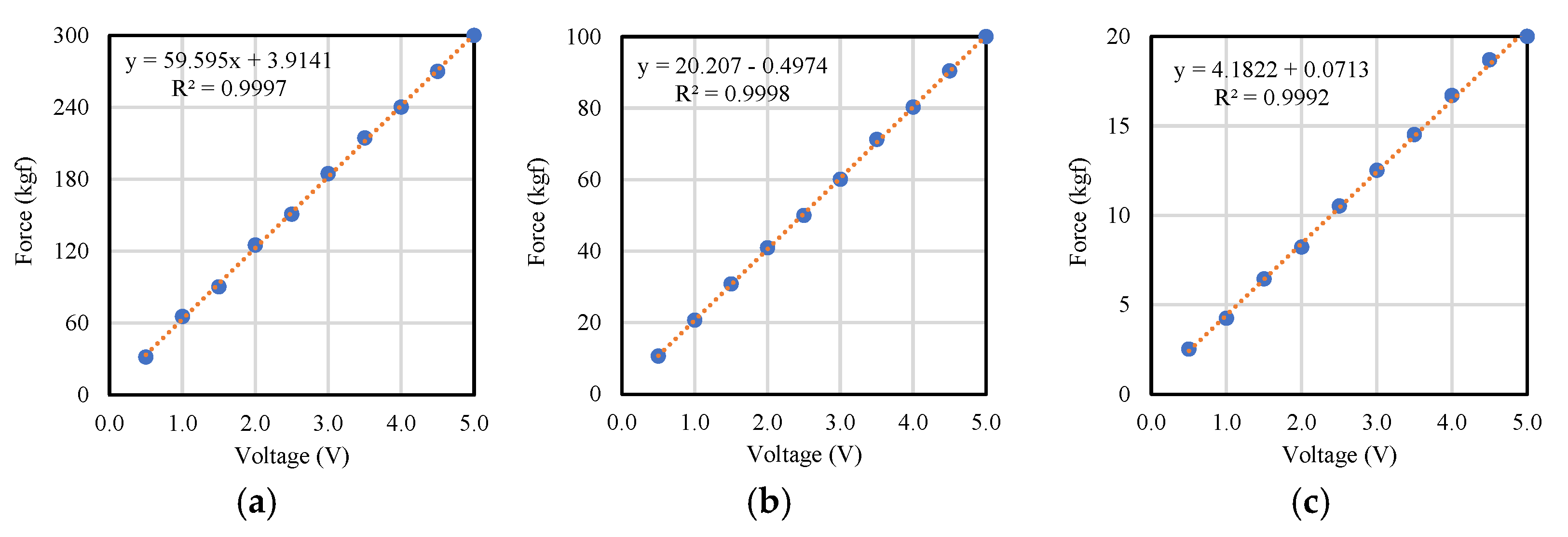
3.3. Static Calibration of Miniature Load Cell
3.4. Implementation and Precision Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sredanović, B.; Carou, D. Monitoring of Cutting Forces in Turning. In Notes for Manufacturing Instructors; Carou, D., Davim, J.P., Eds.; Springer: Cham, Switzerland, 2024; pp. 131–149. [Google Scholar]
- Zhang, J.; Xiao, G.; Yi, M.; Chen, Z.; Wang, L.; Chen, J.; Xu, C. Accurate Cutting-Force Measurement with Smart Tool Holder in Lathe. Sensors 2023, 23, 4419. [Google Scholar] [CrossRef] [PubMed]
- Kumar, P.; Yadav, S. Measurement and Analysis of Cutting Forces Using Dynamometer in Turning of EN-8 Steel. Mater. Today Proc. 2023, in press. [Google Scholar] [CrossRef]
- Panesso, M.; Ettrichrätz, M.; Gebhardt, S.; Georgi, O.; Rüger, C.; Gnauck, M.; Drossel, W.G. Design and Characterization of Piezoceramic Thick Film Sensor for Measuring Cutting Forces in Turning Processes. In Manufacturing Driving Circular Economy: GCSM 2022; Kohl, H., Seliger, G., Dietrich, F., Eds.; Lecture Notes in Mechanical Engineering; Springer: Cham, Switzerland, 2023; pp. 30–39. [Google Scholar]
- Yu Timokhin, I.; Anashkina, A.A.; Kharakhonov, G.A.; Ermolaev, Y.O. Cutting Force Measurement During Machining of the Ceramic Parts Designed for Aviation Purposes. Proc. High. Educ. Inst. Machine Build. 2023, 6, 47–57. [Google Scholar] [CrossRef]
- Uquillas, D.A.R.; Yeh, S.S. Tool Holder Sensor Design for Measuring the Cutting Force in CNC Turning Machines. In Proceedings of the 2015 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Busan, Republic of Korea, 7–11 July 2015; pp. 1218–1223. [Google Scholar]
- Totis, G.; Bortoluzzi, D.; Sortino, M. Development of A Universal, Machine Tool Independent Dynamometer for Accurate Cutting Force Estimation in Milling. Int. J. Mach. Tools Manuf. 2024, 198, 104–151. [Google Scholar] [CrossRef]
- Rizal, M.S.; Ghani, J.A.; Usman, H.; Dirhamsyah, M.; Mubarak, A.Z. Development and Testing of a Stationary Dynamometer Using Cross-beam-Type Force-Sensing Elements for Three-Axis Cutting Force Measurement in Milling Operations. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2023, 238, 950–961. [Google Scholar] [CrossRef]
- Mohanraj, T.; Irfan, M.; Uddin, S.K. Review on Sensor Design for Cutting Force Measurement. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2022, 327, 1–12. [Google Scholar] [CrossRef]
- Khatekar, N.V.; Kalidasan, R.; Pawade, S.R. An FEM-ANN Based Analysis of Cutting Force and Cutting Tool Deflection to Predict Tool Wear in Double Tool Turning Process. Key Eng. Mater. 2023, 959, 67–76. [Google Scholar] [CrossRef]
- Ho, Q.N.; Do, T.T.; Minh, P.S. Studying the Factors Affecting Tool Vibration and Surface Quality during Turning through 3D Cutting Simulation and Machine Learning Model. Micromachines 2023, 14, 1025. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Ren, Z.; Zhang, J.; Li, W.; Jia, Z.; Qian, M. Development of a Shear-Type Dynamometer for High-Temperature Environment. IEEE Sens. J. 2022, 22, 15893–15902. [Google Scholar] [CrossRef]
- Gong, T.; Zhao, Y.; Zhao, Y.; Wang, L.; Yang, Y.; Ren, W. Design and Manufacturing of a High-Sensitivity Cutting Force Sensor Based on AlSiCO Ceramic. Micromachines 2021, 12, 63. [Google Scholar] [CrossRef] [PubMed]
- Song, X.; Wu, W.J.; Zhao, Y.; Cheng, Y.P.; Liu, L. Structural Design and Optimization of the Milling Force Measurement Tool System Embedded with Thin-Film Strain Sensors. Micromachines 2023, 14, 2133. [Google Scholar] [CrossRef] [PubMed]
- Apichatbanlue, U.; Suksawat, B. Data Acquisition System for Main Cutting Force Measurement in Turning Operation. In Proceedings of the 2011 11th International Conference on Control, Automation and Systems, Gyeonggi-do, Republic of Korea, 26–29 October 2011; pp. 1003–1005. [Google Scholar]
- Liu, Y.; Chen, C.; Li, F.Z.; Zhang, Y.; Ju, B.F.; Lin, H. Three-Axial Cutting Force Measurement in Micro/Nano-Cutting by Utilizing a Fast Tool Servo with A Smart Tool Holder. CIRP Ann. 2021, 70, 33–36. [Google Scholar]
- Youssef, H.; El-Hofy, H. Traditional Machining Technology, 2nd ed.; Deanta Global: Chennai, India, 2020. [Google Scholar]
- Boothroyd, G.; Knight, W.A. Fundamentals of Metal Machining and Machine Tools, 2nd ed.; McGraw-Hill: New York, NY, USA, 1989. [Google Scholar]
- Zhang, F.; Zhao, J.; Zhang, X. Estimation of Relative Standard Deviation Related to Limit of Detection and Limit of Quantitation. AHFE Int. 2023, 104, 36–40. [Google Scholar]
- Prasad, M.; Snyderman, N.J.; Verbeke, J. Analytical Error Bars and RSD for Neutron Multiplicity Counting. Nucl. Instrum. Methods Phys. Res. A 2018, 903, 25–31. [Google Scholar] [CrossRef]

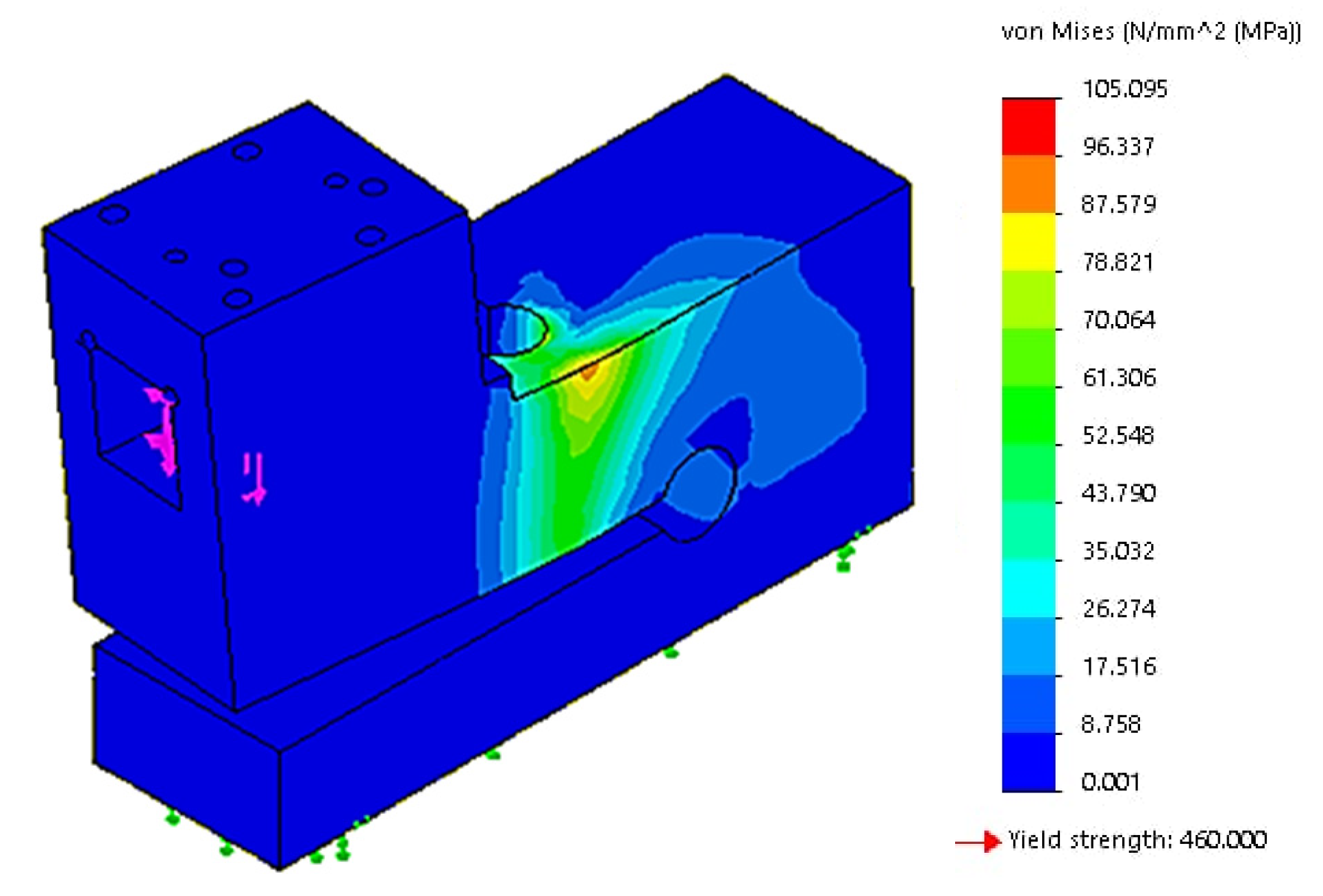



| No. | R1 (mm) | L1 (mm) | Deflection 1 (µm) | R2 (mm) | L2 (mm) | Deflection 2 (µm) | Max. Von Mieses Stress (MPa) | Safety Factor |
|---|---|---|---|---|---|---|---|---|
| 1 | 4 | 32 | 4.58 | 8 | 70 | 5.75 | 86.172 | 5.338 |
| 2 | 5 | 32 | 5.23 | 8 | 70 | 6.70 | 85.337 | 5.390 |
| 3 | 6 | 32 | 6.55 | 8 | 70 | 7.96 | 95.160 | 4.834 |
| 4 | 7 | 32 | 8.81 | 8 | 70 | 9.89 | 105.095 | 4.377 |
| 5 | 8 | 32 | 8.00 | 8 | 70 | 8.62 | 121.713 | 3.779 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khammongkhon, N.; Niropas, P.; Pomusa, C.; Suksawat, B. Development and Implementation of Modular Turning Dynamometer with Miniature Load Cell. Eng. Proc. 2025, 84, 43. https://doi.org/10.3390/engproc2025084043
Khammongkhon N, Niropas P, Pomusa C, Suksawat B. Development and Implementation of Modular Turning Dynamometer with Miniature Load Cell. Engineering Proceedings. 2025; 84(1):43. https://doi.org/10.3390/engproc2025084043
Chicago/Turabian StyleKhammongkhon, Naruebet, Phanuwat Niropas, Chanikan Pomusa, and Bandit Suksawat. 2025. "Development and Implementation of Modular Turning Dynamometer with Miniature Load Cell" Engineering Proceedings 84, no. 1: 43. https://doi.org/10.3390/engproc2025084043
APA StyleKhammongkhon, N., Niropas, P., Pomusa, C., & Suksawat, B. (2025). Development and Implementation of Modular Turning Dynamometer with Miniature Load Cell. Engineering Proceedings, 84(1), 43. https://doi.org/10.3390/engproc2025084043






