Analysis of GNSS Signal Correlation in Terrestrial Vehicles ^†

Abstract

This paper deals with the analysis of the distortion of the correlation functions in real vehicular scenarios. A multicorrelator GNSS receiver is used to process the data collected in urban and rural environments. Two methods are proposed to evaluate the distortion of the correlation functions due to the presence of multipath. The first one consists of analyzing the error of the estimated correlation functions and the second one is based on estimating the multipath signals by implementing a Non-linear Least Squares (NLS) algorithm. The paper determines the number of reflected signals and assesses the differences and similarities between both scenarios.

1. Introduction

Multipath is one of the major sources of positioning error in Global Navigation Satellite System (GNSS) receivers. Efficient techniques to suppress and eliminate multipath errors are of remarkable importance since there is currently no way to completely remove them. When the GNSS receiver is surrounded by obstacles, a portion of the electromagnetic wave broadcast by a satellite travels in a straight line to the receiver, while other portions might reach the receiver due to reflection or refraction caused by the surrounding objects. Multipath refers to the phenomenon where the GNSS receiver receives both electromagnetic wave signals. One or more multipath signals can be received in adverse environments, particularly in urban scenarios [1].

The presence of multipath introduces errors in code delay and carrier phase measurements of GNSS receivers. This occurs because the GNSS receiver is tracking the superposition of several signals (the desired/direct signal and the multipath components), which creates some deformation in the correlation function, leading to an incorrect estimate of the time of arrival. The correlation function provides crucial information about the presence of reflected signals. However, most of the mass-market GNSS receivers do not provide correlator outputs, while some high-end GNSS receivers can output a few of them. This happens because the implementation of additional correlators involves an increase in the computation burden of the receiver.

Research on multicorrelator receivers is available in the literature [2,3], along with analyses on multipath distribution in urban canyons [4], but the multipath is still a problem in GNSS receivers. For this reason, it is necessary to continue the research on multipath exploiting the advances of GNSS receivers. Performing analyses with multicorrelator receivers, which provide a large number of correlators, using long datasets with live signals collected in vehicles is still a challenging task. This could be explained by the fact that, in general, many correlator outputs can only be obtained by software receivers, but they usually require a huge amount of time to process the signal during long periods. In this work, we highlight the benefits of having a real-time hardware multicorrelator receiver to estimate the multipath components in real propagation channels.

This paper analyzes the GNSS signal correlations estimated by a multicorrelator GNSS receiver in real vehicular scenarios. The scenarios were recorded with the Spirent GSS6450 and replayed in the laboratory. The test campaigns were performed driving in two contrasting propagation environments. Rotterdam downtown was chosen to assess the multipath in challenging urban conditions (i.e., in the presence of obstacles such as buildings or structures with multiple heights and including areas with urban canyons where satellite visibility is certainly degraded). Nieuw-Vennep was selected as an open-sky/rural environment where there are practically no obstacles between the antenna and the satellites [5]. More information about the accuracy provided by GNSS receivers in these environments can also be found in [5].

The objective is to characterize the multipath of the received signal using a high-end GNSS receiver able to store 41 correlator outputs in the range between −1 and 1 chip. The multipath error is estimated by comparing a local reference of the correlation function, which is estimated by using a GNSS simulator in the absence of GNSS disturbances, to the correlations estimated by the GNSS receiver. Two methods are considered. The first one consists of computing the error between the reference correlation function and the estimated ones. We evaluate the impact of the multipath on the temporal domain. The second one is based on estimating the multipath by implementing a Non-linear Least Squares (NLS) estimator. The estimator provides reliable information about the power of the direct and reflected signals and the number of received signals. We analyze the differences and similarities between both scenarios for several satellites with different elevations.

2. Signal Model

Upon reaching the receiving antenna, the GNSS signal is filtered, down-converted, and digitalized to obtain a complex baseband signal. Subsequently, the baseband signal is correlated with local replicas of the Pseudorandom Noise (PRN) code. The outcome of the correlation is accumulated over a specific time interval to be able to acquire the received signal [6,7].

In the presence of the multipath effect, the received signal at the antenna is a combination of both the direct satellite wave and the reflected waves. The processed signal at the receiver is a superposition of these waves, and it becomes a challenging task to distinguish between the direct wave and the individual reflected waves. When a receiver computes the cross-correlation function with the replica of a PRN in the tracking stage, this PRN code is correlated simultaneously with both the reflected and direct waves. As a result, the final output is a superposition of these correlation values. The resulting correlator outputs for a particular signal, satellite, and time instant, considering the presence of several multipath components, and after the removal of the navigation data the Doppler frequency shift can be written as follows [1,2]:

$$y_k=I_k+j{Q}_k=\sum _{l=1}^L{A}_{l}R\left({\delta }_k-{\tau }_l\right)e^{j{\phi }_l}+{\omega }_k$$

(1)

where $R\left(\tau \right)$ represents the cross-correlation function between the ideal PRN code and a low-pass filtered version of the PRN code; ${\mathsf{\omega }}_k$ is a complex Gaussian random variable after computing the correlation; and $A_l$, ${\tau }_l$, and ${\phi }_l$ are, the amplitude, delay, and phase of the lth ray, respectively. The subscript $k=-M,\dots ,M$ defines the correlator location, being k = 0 for the prompt, ${\delta }_k$ is the correlator delay, and $L$ defines the number of received signals, being $l=1$ for the Line-of-Sight (LOS) signal. Equation (1) can be expressed in vectorial form as

$$\mathbf{y}=\mathbf{R}\left(\mathsf{\tau }\right)\mathsf{\alpha }+\mathsf{\omega }$$

(2)

where:

$\mathbf{y}={\left[y\left(-M\right),..,y\left(M\right)\right]}^{\mathrm{T}}$ is a 2M+1 x 1 vector containing the complex samples of the estimated correlations,

$\mathsf{\omega }$ = ${\left[{\omega }_{-M},..,{\omega }_M\right]}^{\mathrm{T}}$ is a 2M+1 x 1 vector including the Gaussian noise samples,

$\mathbf{R}\left(\tau \right)$ is a 2M+1 x L matrix depending on the unknown time delays as

$$\mathbf{R}\left(\mathsf{\tau }\right)=\left[\begin{array}{ccc}R\left({\delta }_{-M}-{\tau }_1\right)& \cdots & R\left({\delta }_{-M}-{\tau }_L\right)\\ ⋮& \ddots & ⋮\\ R\left({\delta }_M-{\tau }_1\right)& \cdots & R\left({\delta }_M-{\tau }_L\right)\end{array}\right],$$

(3)

$\mathsf{\alpha }$ = ${\left[A_1{e}^{j{\phi }_1},..,A_L{e}^{j{\phi }_L}\right]}^{\mathrm{T}}$ is an Lx1 unknown vector that depends on the amplitudes and phases of the received signals. Note that $A_1{e}^{j{\phi }_1}$ denotes the magnitude of the LOS signal.

The cross-correlation function not only depends on the transmitted signal but also on the receiver’s front end. In order to have an accurate estimate of the cross-correlation function, a test was performed with the GSS9000 GNSS simulator. In particular, the simulator was transmitting a GNSS signal in ideal conditions (i.e., with high C/N₀ and in the absence of GNSS disturbances such as multipath) and the receiver was gathering GNSS signal correlation data. The reference correlation was estimated by averaging the received correlation data for a certain period of time to reduce the contribution of the noise.

3. Key Point Indicator Metrics

This section describes the method used to quantify the error of the GNSS signal correlation estimated from the different environments. These correlator outputs contain an unknown amplitude, which depends on the received power. In order to remove this amplitude, the I components can be normalized by the prompt magnitude as

$${\displaystyle \frac{I_k}{I_0}}$$

(4)

where $I_0$ is the real component of the prompt at the output of the tracking stage that usually exhibits the highest magnitude of the correlation function. In general, in ideal conditions of signal reception, most of the energy is concentrated on the real part because the tracking loop tries to remove the phase of the received signal. One way to quantify the error between the reference correlation and the received ones is by computing the Root Mean Square Error (RMSE).

$$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}\left({\displaystyle \frac{I_k}{I_0}},{\displaystyle \frac{I_k^{reference}}{I_0^{reference}}}\right)$$

(5)

where $I_k^{reference}$ is the reference correlation function. To compute the RMSE, it is important to split the received data among several C/N₀ regions. Since, if the estimated C/N₀ is low, the received signal is more prone to suffer from the multipath effect due to the possible presence of obstacles that are causing the signal degradation. On the contrary, if the C/N₀ is very high, the elevation of the satellite is probably high, and the multipath effect tends to be smaller or even negligible.

4. Non-Linear Least Squares

The multipath estimation problem can be written by an NLS cost function defined as follows:

$$J\left(\mathsf{\alpha },\mathsf{\tau }\right){=‖\mathbf{y}-\mathbf{R}\left(\mathsf{\tau }\right)\mathsf{\alpha }‖}^2.$$

(6)

The definition of the vectors and matrices can be found in Section 2. This cost function depends on two unknown vectors, $\mathsf{\alpha }$ and $\mathsf{\tau }$. The received signals can be estimated by finding the best fit between the estimated correlations, $\mathbf{y}$, and the assumed signal model, $\mathbf{R}\left(\mathsf{\tau }\right)\mathsf{\alpha }$. This model is not linear with $\mathsf{\tau }$ but is linear with $\mathsf{\alpha }$. In order to find the unknown magnitudes, $\mathsf{\alpha }$ and $\mathsf{\tau }$, that minimize the cost function, we can apply the separability property [8,9]. First, the linear parameter is replaced by its least squares solution so that the cost function only depends on the non-linear parameter, which is given by

$$\widehat{\mathsf{\alpha }}={\left({\mathbf{R}}^{\mathrm{H}}\left(\mathsf{\tau }\right)\mathbf{R}\left(\mathsf{\tau }\right)\right)}^{-1}{\mathbf{R}}^{\mathrm{H}}\left(\mathsf{\tau }\right)\mathbf{y}.$$

(7)

Second, the problem now reduces to the minimization of

$$J\left(\widehat{\mathsf{\alpha }},\mathsf{\tau }\right){=‖\mathbf{y}-\mathbf{R}\left(\mathsf{\tau }\right)\widehat{\mathsf{\alpha }}‖}^2.$$

(8)

To perform this minimization, we have used the fmincon function from Matlab (https://www.mathworks.com/help/optim/ug/fmincon.html, (accessed on 14 March 2025)), which finds the minimum of constrained non-linear multivariable functions. It is worth mentioning that the number of rays is unknown by the user and the selection of this parameter is essential to obtain an accurate estimate of the multipath. More details are included in Section 6.

5. Setup Description

The GNSS data analyzed in this paper was collected with the van of the ESA Navigation Laboratory using the GSS6450 record and playback system. As we previously described, the data were gathered in two contrasting propagation environments: Rotterdam and Nieuw-Vennep. While Rotterdam downtown was selected to describe the receivers’ performance in an authentic urban/challenging environment, Nieuw-Vennep was chosen to analyze the user-level performance in open-sky/rural conditions. In the past, ESA selected these scenarios to evaluate the performance of GNSS receivers. Figure 1 depicts the route taken in the downtown area of Rotterdam as well as the typical rural Nieuw-Vennep elements [5].

The data were replayed in the ESA Navigation Laboratory (https://technology.esa.int/lab/navigation-laboratory (accessed on 14 March 2025)). The real-time hardware multicorrelator receiver used to collect the measurements is a Septentrio receiver with a special FW version. This version allows us to store and configure the location of 41 correlator outputs for 4 GPS and 4 Galileo satellites. The receiver can simultaneously provide these measurements for GPS L1C/A, GPS L5, Galileo E1, and Galileo E5a. In this paper, we only analyze the correlator outputs estimated for GPS L1 C/A. The analysis for the rest of the signals is left as future work.

6. Results

This section describes the results obtained from the data collected in Nieuw-Vennep and Rotterdam. Each campaign has a duration of around 2 h. The Nieuw-Vennep and Rotterdam campaigns were performed on 14 February 2023 and 31 January 2023, respectively. The results are divided into two subsections. The first subsection describes the difference between the error of correlation function in the rural (Niew-Vennep) and urban (Rotterdam) environments. The second subsection focuses on estimating the multipath of the received signal by using an NLS estimator for satellites with different elevations in both scenarios.

6.1. Analysis of GNSS Signal Correlations

Figure 2a,b show the comparison between the normalized correlation functions of PRN 32 in the two scenarios. The elevation of the satellite is comprised approximately between 5 and 40 degrees in both scenarios. As expected, higher distortion is observed in Rotterdam, since this scenario contains the presence of many obstacles in the propagation path between the satellite and the receiver. The lower the C/N₀, the more distorted the correlation functions are. However, we can also distinguish some correlations with little distortion with respect to the reference correlation function and high C/N₀. This indicates that, in a realistic urban scenario, the signal can also be received without significant multipath. On the contrary, the correlator outputs observed in Nieuw-Vennep are more similar to the reference correlation function for all of the C/N₀ ranges, although for low C/N₀ values these correlations tend to provide a larger error because they are noisier.

Figure 2c shows the RMSE between the reference and estimated correlation functions, including data from several satellites. Comparing Rotterdam (urban) and Nieuw-Vennep (rural), the conclusions below can be drawn.

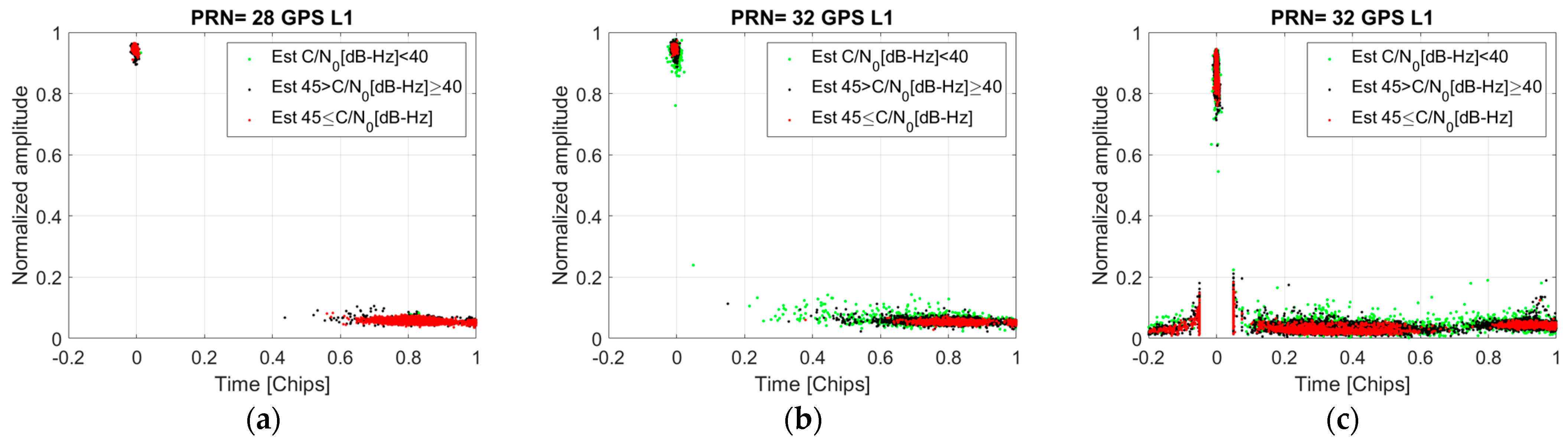
• The urban scenario provides higher RMSE magnitudes than the rural scenario due to the multipath effect. In the urban scenario, correlation functions with low C/N₀ are more affected by multipath, causing a higher error with respect to the reference correlation function. Comparing the outcome for C/N₀ values below 40 dB-Hz, the rural scenario offers much lower RMSE values than the urban scenario. The former is mostly affected by the presence of noise, while the latter is affected not only by noise but also by multipath.
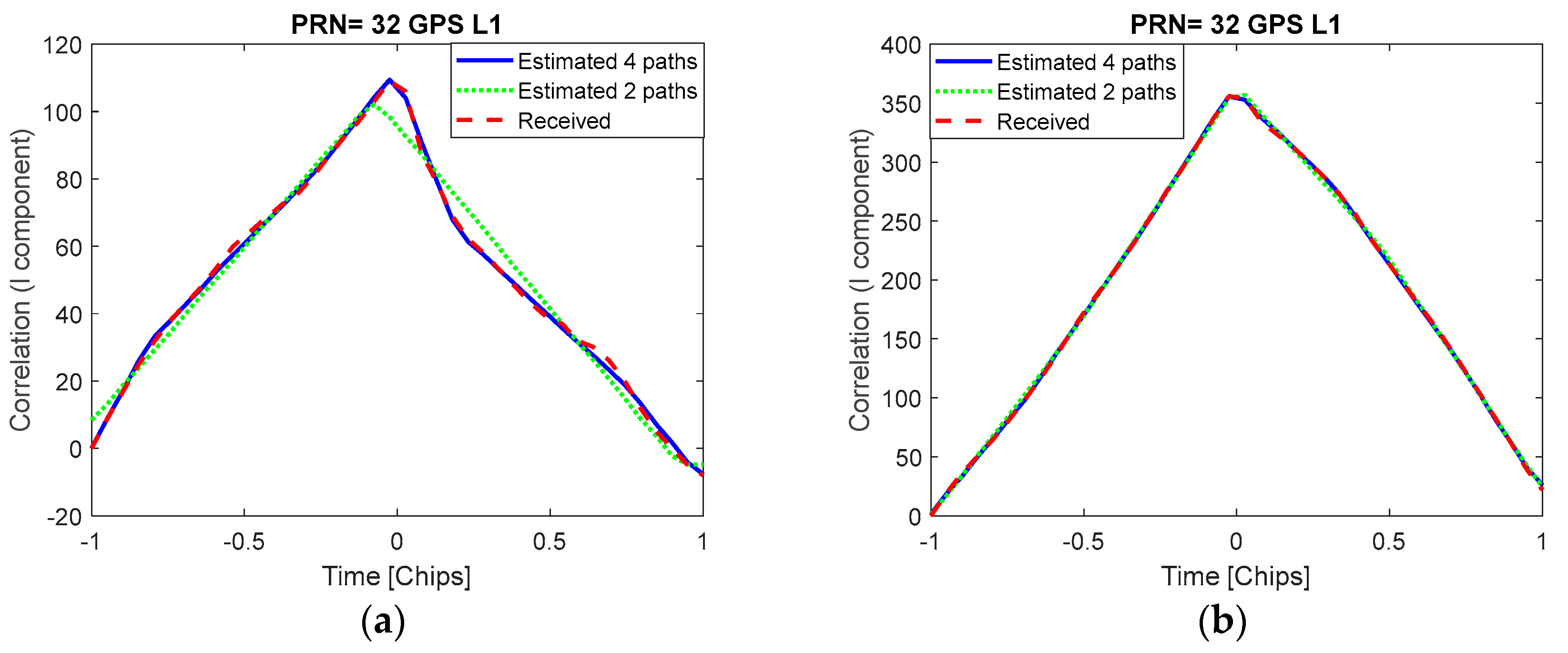
• The right part of the normalized correlation functions is more distorted than the left part. This occurs because the reflections are probably received after the LOS impacts largely the right part of the correlation functions. The correlations computed from the reflected signals exhibit the highest magnitudes after the peak of the LOS correlation, which is being tracked most of the time by the receiver.
• In some periods of time in the urban scenario, satellite signal visibility is clean (often high-elevation satellites are less affected by multipath); therefore, the signal is received with high C/N₀ (higher than 45 dB-Hz). In these periods, the RMSE of both scenarios is relatively similar.

6.2. Multipath Estimation

The NLS allows us to estimate the LOS and reflected signals. Two different configurations are implemented. On the one hand, a four-path model is considered for the urban environment; that is, we assume that $L$, the number of incoming signals, is 4. Empirically, we observe that the four-path model provides an excellent fit between the received correlation functions and the estimated ones, resulting in a small error in the cost function. On the other hand, we consider a two-path model for the rural environment. This model is enough because, most of the time, the received signal only contains the LOS signal.

As we described in Section 4, the fmincon function, which finds the minimum of a constrained non-linear multivariable function, is used to estimate the unknown time delays of the received signals. The minimization problem can lead to an erroneous solution if the delays of two signals have practically the same value and their amplitudes are similar but with opposite signs. If this occurs, the algorithm can estimate two fictitious signals that are not present in the received signal. To circumvent this problem, we add some constraints in the algorithm so that the minimum delay between two signals must be at least 1 sample. By doing so, we remove the incorrect estimate of GNSS signals at the cost of not being able to estimate multipath components that are closer than one sample.

The correlator outputs estimated by the receiver usually have the highest magnitude near the prompt (i.e., chip time equal to 0; see Figure 2). For the fourth-path model, we consider that the main signal is located at a time instant close to 0, and we initialize the algorithm to find a signal around this delay. Then, we also consider two multipath signals after the main one, but the multipath signals must be delayed by at least one sample from the main one and between them. Finally, we include in the model a multipath signal before the prompt and with a separation of at least one sample with the main signal. For the two-path model, we only consider the LOS signal and a reflected signal. The minimum delay between both signals is forced in the algorithm to be one sample to avoid the previously mentioned issue related to the estimation of incorrect signals. In the cases where there are fewer signals in the received data than the ones included in the model, the algorithm estimates a low magnitude for the missing signals.

Figure 3 shows an example of the real part of the received correlation and the real part of the estimated correlation defined as $\widehat{\mathbf{y}}=\mathbf{R}\left(\widehat{\mathsf{\tau }}\right)\widehat{\mathsf{\alpha }}$, where the matrices are defined in Section 4, in the urban environment. The results show that, when the correlation function is considerable distorted (left figure), the two-path model is not accurate enough and exhibits a significant error with respect to the received correlation function. However, using the four-path model, the estimated and received correlation functions match remarkably well during the whole test. In cases where the correlation is less deformed (right figure), the two-path model also offers a remarkable performance.

Table 1. Satellite elevation description.

Scenario	PRN	Lowest Elevation	Highest Elevation
Rotterdam	25	51	86
Rotterdam	12	23	86
Rotterdam	32	5	40
Nieuw-Vennep	28	31	62
Nieuw-Vennep	32	0	40

summarizes the elevation of the satellites analyzed in this paper. For the urban scenario, three satellites with low, high, and medium elevations are assessed, while for the rural environment, two satellites with low and medium elevations are evaluated. The NLS is computed for all of the satellites included in this table.

Figure 4 shows the normalized amplitude (defined as $A_l/\sum _{l=1}^L{A}_l$) at the time delay ${\tau }_l$ obtained from the NLS estimator in the urban scenario. The outcome shows that the elevation and C/N₀ are parameters that are highly correlated with the presence of multipath. The signal received from PRN 32 is the one that is most affected by multipath, especially for low C/N₀ values (green dots). The amplitude of the reflected signals tends to decrease when the delay of the reflected signal is larger. When the estimated C/N₀ is between 40 and 45 dB-Hz, the multipath effect is usually less significant than for a lower C/N₀ region. For C/N₀ values larger than 45 dB-Hz, the results for all satellites are considerably similar, showing only one main peak and some residual noise or negligible multipath compared to the one obtained in the other C/N₀ regions. In general, the signal received from the satellite with high/medium elevation (PRN 12) includes less severe multipath compared to the satellite with the lowest elevation (PRN 32), although some reflections are observed with a large amplitude and with a delay of about 0.7 chips (PRN 12). The normalized amplitudes of the reflected signals for the satellite with high elevation (PRN 25) are lower than that of PRN 32 and 12.

Figure 5 shows the normalized amplitude (defined as $A_l/\sum _{l=1}^L{A}_l$) at the time delay ${\tau }_l$ obtained from the NLS estimator in the rural scenario. As expected, the presence of multipath in this scenario is negligible due to the mild conditions of signal reception. Comparing the two-path model for PRN 28 and 32 (left and middle figures), the data from both satellites provide similar results, showing the LOS and a residual estimate for the second path. In this scenario, the received signal is not affected by strong multipath and the LOS component is clearly dominant. In this case, it is interesting to compare the outcome from the two-path model and the four-path model (middle and right figures). Both models estimate the LOS signal and a residual amplitude for the other signals. The magnitude of the normalized amplitude is slightly different in both models since the four-path model estimates three residual amplitudes and the two-path model estimates only one residual magnitude. The magnitude of the LOS signal is slightly smaller for the four-path model because it is normalized to include three residual amplitudes ($\sum _{l=2}^4{A}_l$), and the two-path model only considers one residual amplitude ($\sum _{l=2}^2{A}_l$). Comparing the four-path model obtained in the rural scenario for the low-elevation satellite (PRN 32, Figure 5), and in the Rotterdam scenario for the high-elevation satellite (PRN 25, Figure 4), we can notice relatively similar results, although the data from PRN 25 illustrate slightly higher values near the prompt. On the contrary, when comparing the results in both scenarios for the low-elevation satellites (PRN 32, Figure 4 and Figure 5), we can observe that the received signals from the urban scenario are much more affected by multipath.

7. Conclusions

This paper has exploited the advantages of using a real-time hardware multicorrelator receiver to analyze the multipath components in real vehicular scenarios. We have quantified the error of the correlator outputs, illustrating that most of the distortion is present on the right part of the correlation function, and shown the relationship between the C/N₀ and the error. Moreover, we have revealed that, for the analyzed urban scenario, a four-path model provides an excellent fit with the received signals. The signals received from satellites with low elevations in urban areas are the ones most affected by multipath components. The limitations of the NLS estimator have been described, showing that the multipath signals received with a delay smaller than the distance between consecutive correlator outputs are difficult to distinguish. The rural scenario has clearly exhibited less multipath than the urban scenario. Nonetheless, in the urban scenario, GNSS signals are also received with high C/N₀ (>45 dB-Hz) during some periods of time, and in these cases the error in the correlation function is close to the one provided in the rural environment.

8. Future Work

The future work consists of performing a similar analysis for different signals (e.g., GPS L5, Galileo E1, Galileo E5a). Moreover, we are creating an extensive dataset that includes correlator outputs for different scenarios, such as spoofing, jamming, and multipath, with the aim of analyzing the benefits of machine-learning algorithms to classify the data.