Cattaneo-Christov Heat Flux Model Effect on Magnetized Maxwell Nanofluid Flow over a Stretching Surface †
Abstract
:1. Introduction
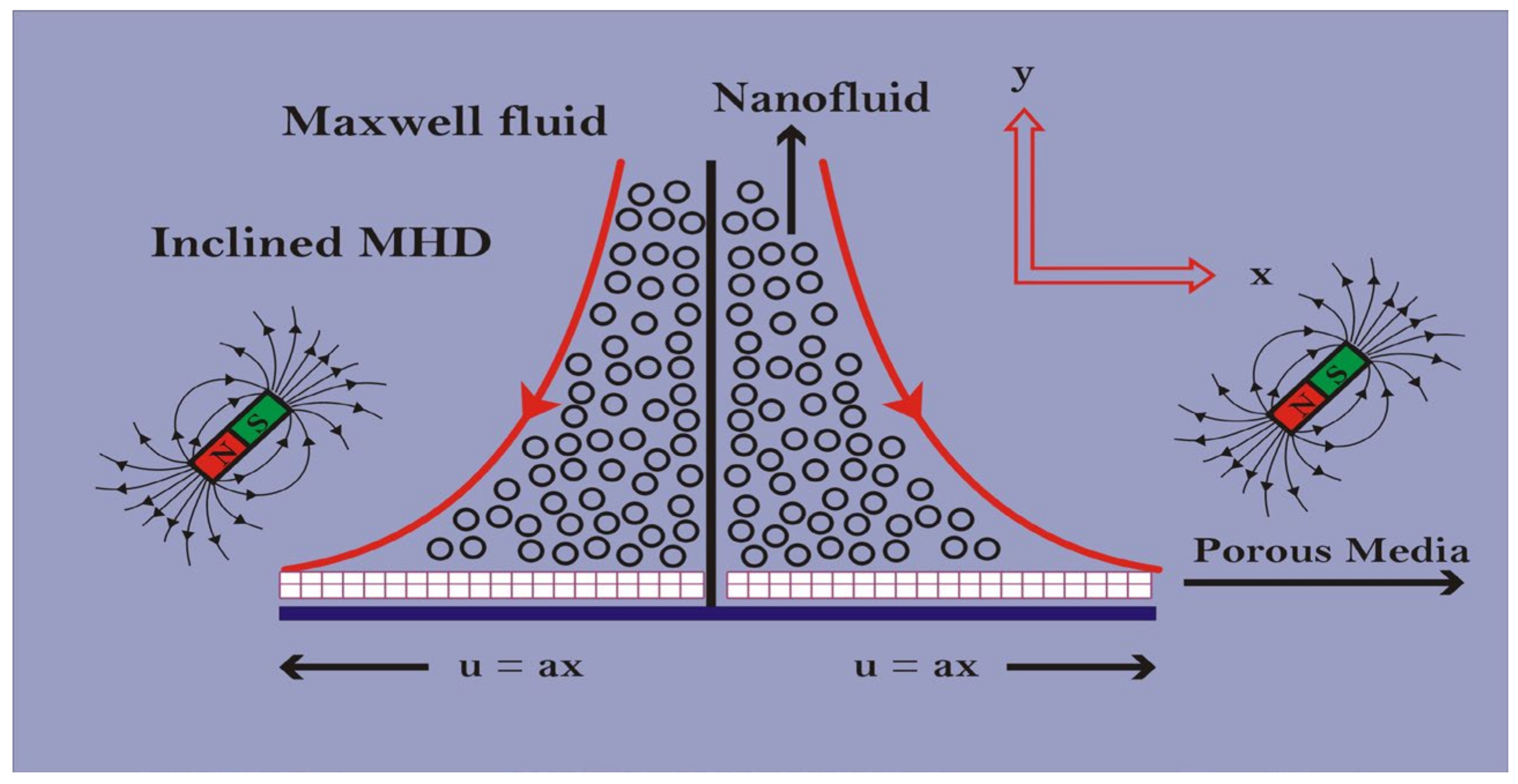
2. Mathematical Formulation
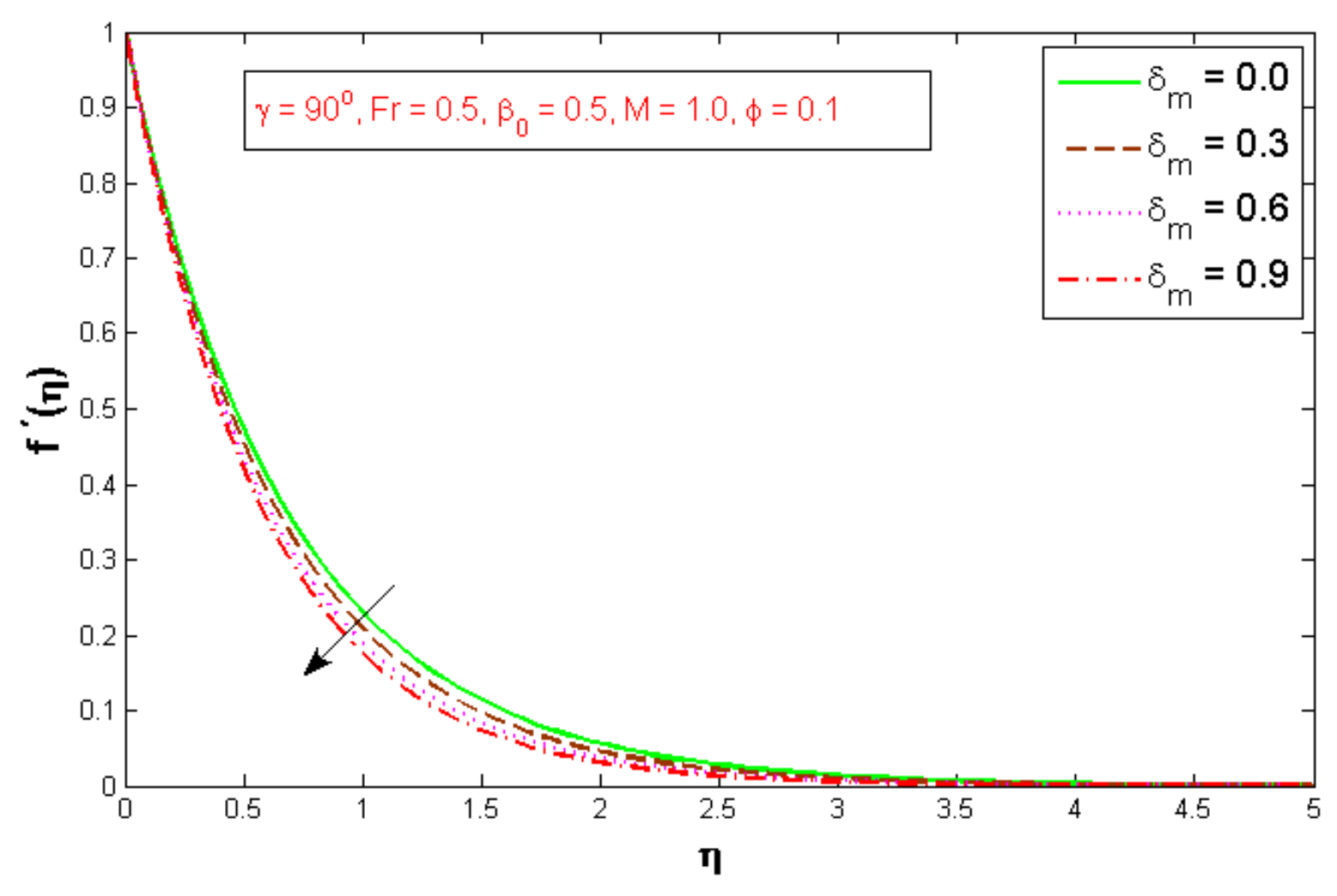
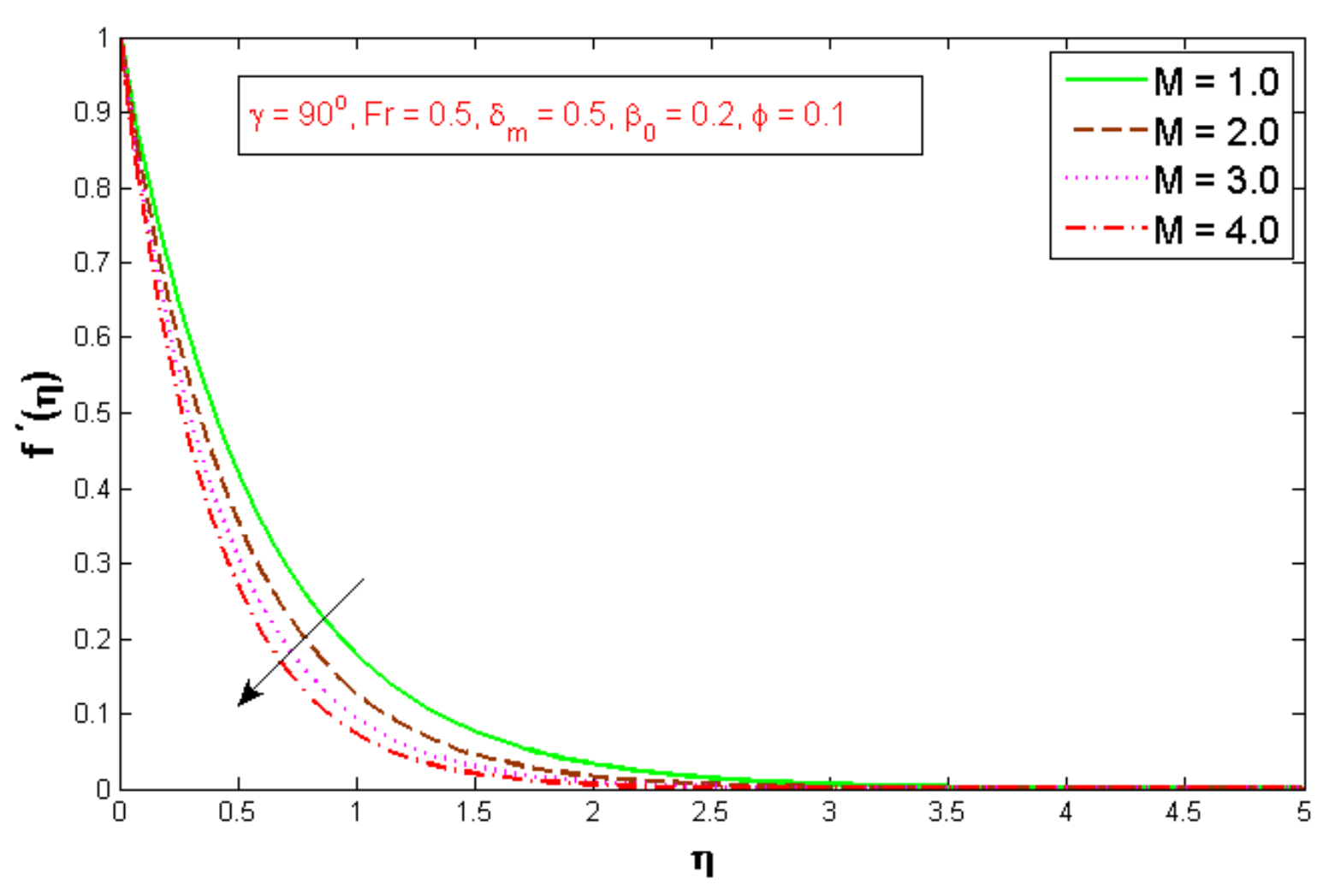
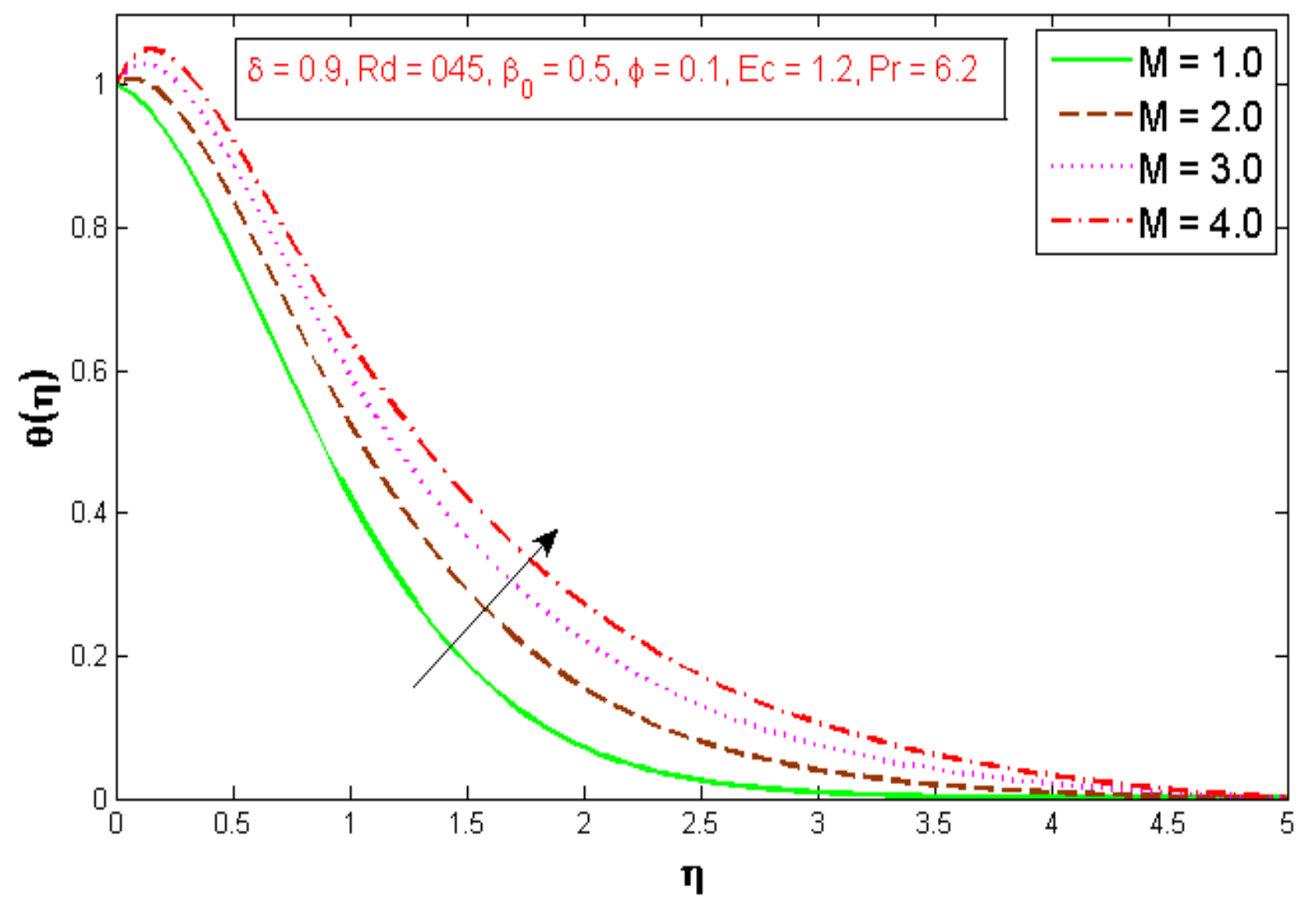
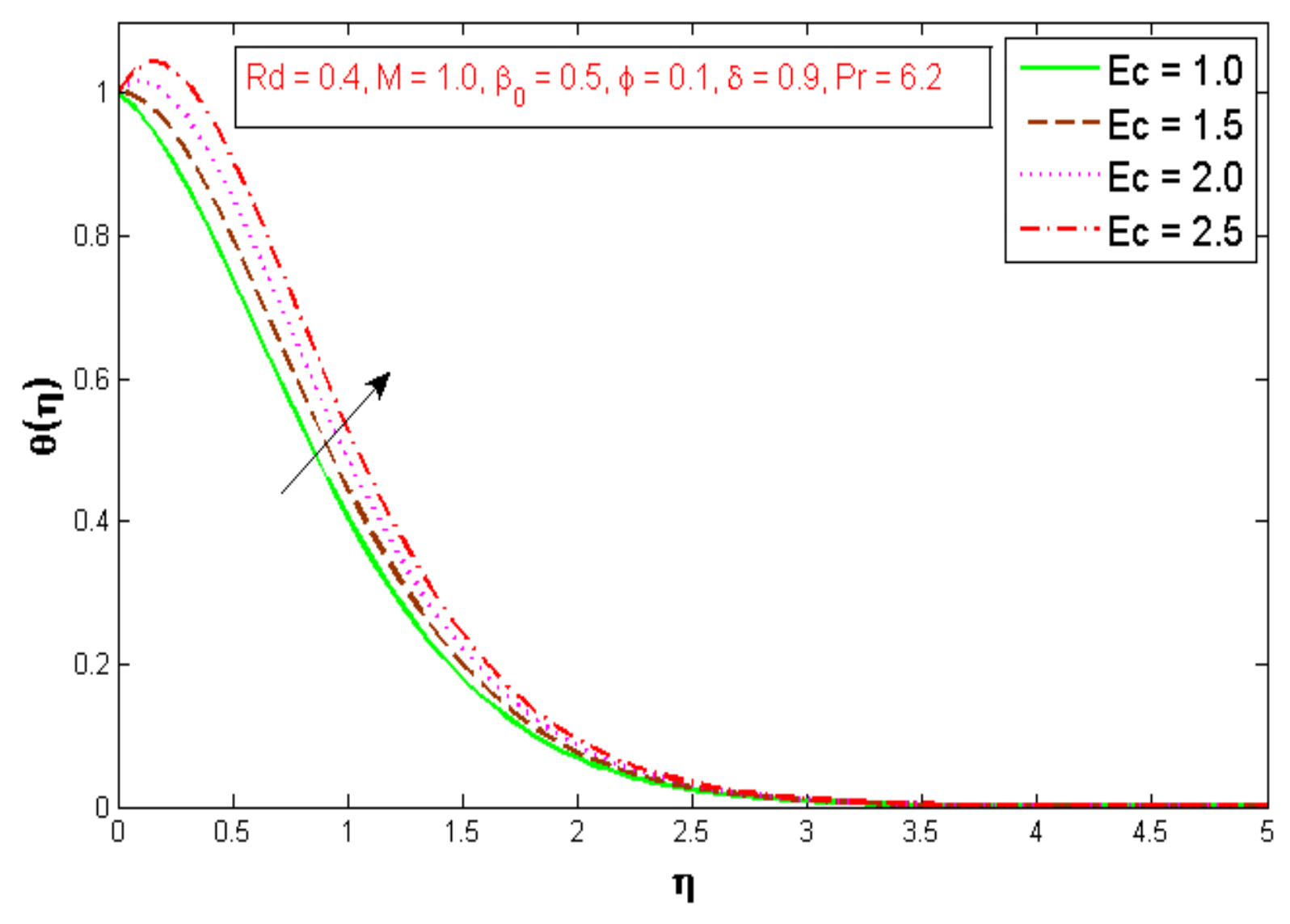
3. Results and Discussions
4. Conclusion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Saeed, A.; Kumam, P.; Gul, T.; Alghamdi, W.; Kumam, W.; Khan, A. Darcy-Forchheimer couple stress hybrid nanofluids flow with variable fluid properties. Sci. Rep. 2021, 11, 19612. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Raghunath, K.; Alfaleh, A.; Ali, F.; Zaib, A.; Khan, M.I.; ElDin, S.M.; Puneeth, V. Effects of activation energy and chemical reaction on unsteady MHD dissipative Darcy-Forchheimer squeezed flow of Casson fluid over horizontal channel. Sci. Rep. 2023, 13, 2666. [Google Scholar] [CrossRef] [PubMed]
- Bandaru, M.; Vijaya, R.B. Effect of variable thermal conductivity on convective heat and mass transfer over a vertical plate in a rotating system with variable porosity regime. J. Nav. Archit. Mar. Eng. 2014, 11, 83–92. [Google Scholar] [CrossRef]
- Hayat, T.; Haider, F.; Muhammad, T.; Alsaedi, A. Three-dimensional rotating flow of carbon nanotubes with Darcy-Forchheimer porous medium. PLoS ONE 2017, 12, e0179576. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, M.W.; Kumam, P.; Shah, Z.; Farooq, A.A.; Nawaz, R.; Dawar, A.; Islam, S.; Thounthong, P. Darcy-Forchheimer MHD Couple Stress 3D Nanofluid over an Exponentially Stretching Sheet through Cattaneo–Christov Convective Heat Flux with Zero Nanoparticles Mass Flux Conditions. Entropy 2019, 21, 867. [Google Scholar] [CrossRef]
- Etwire, C.J.; Seini, I.Y.; Musah, R.; Makinde, O.D. Effects of Temperature Fluctuations on Darcy-Forchheimer Flow of Oil-Based Nanofluid with Activation Energy and Velocity Slip. Earthline J. Math. Sci. 2023, 11, 115–143. [Google Scholar] [CrossRef]
- Majeed, A.; Zeeshan, A.; Noori, F.M. Numerical Study of Darcy-Forchheimer Model with Activation Energy Subject to Chemically Reactive Species and Momentum Slip of Order Two. 2019. Available online: https://pubs.aip.org/ (accessed on 15 September 2023).
- Macía, Y.M.; Soto AA, R.; Gonzalez SM, N.; Yanes, J.P. Parametric Study of Electronic Cooling by Means of a Combination of Crossflow and an Impinging Jet. IEEE Access 2022, 10, 103749–103764. [Google Scholar] [CrossRef]
| Nanoliquid Physical Properties | ||||
|---|---|---|---|---|
| Base Liquid (Water) | 4179 | 997.1 | 0.613 | 0.05 |
| Copper | 385 | 8933 | 400 | 5.97 × 107 |
| Alumina | 765 | 3970 | 40 | ------ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jameel, M.; Shah, Z.; Khan, M.S.; Ullah, N. Cattaneo-Christov Heat Flux Model Effect on Magnetized Maxwell Nanofluid Flow over a Stretching Surface. Mater. Proc. 2024, 17, 12. https://doi.org/10.3390/materproc2024017012
Jameel M, Shah Z, Khan MS, Ullah N. Cattaneo-Christov Heat Flux Model Effect on Magnetized Maxwell Nanofluid Flow over a Stretching Surface. Materials Proceedings. 2024; 17(1):12. https://doi.org/10.3390/materproc2024017012
Chicago/Turabian StyleJameel, Muhammad, Zahir Shah, Muhammad Salim Khan, and Nekmat Ullah. 2024. "Cattaneo-Christov Heat Flux Model Effect on Magnetized Maxwell Nanofluid Flow over a Stretching Surface" Materials Proceedings 17, no. 1: 12. https://doi.org/10.3390/materproc2024017012
APA StyleJameel, M., Shah, Z., Khan, M. S., & Ullah, N. (2024). Cattaneo-Christov Heat Flux Model Effect on Magnetized Maxwell Nanofluid Flow over a Stretching Surface. Materials Proceedings, 17(1), 12. https://doi.org/10.3390/materproc2024017012







