Multiscale Correlation Analysis between Wind Direction and Meteorological Parameters in Guadeloupe Archipelago

Abstract

In this paper, the wind direction ($WD$) behaviour with respect to the variability of other meteorological parameters (i.e., rainfall (R), temperature (T), relative humidity ($Rh$), solar radiation ($SR$) and wind speed (U)) was studied in a multi-scale way. To carry out this study, the Hilbert–Huang transform (HHT) framework was applied to a Guadeloupe archipelago dataset from 2016 to 2021. Thus, the time-dependent intrinsic correlation (TDIC) analysis based on multivariate empirical mode decomposition (MEMD) was performed. For time scales between ∼3 days and ∼7 months, the localized positive and negative correlations between $WD$ and the meteorological parameters have been identified. The alternation between these correlations was more significant for T and $Rh$. With regard to $SR$ and U, there was a dominance of a negative correlation with $WD$. We assumed that the micro-climate previously identified in the literature for the study area plays a key role in these behaviours. A strong positive correlation between $WD$ and R was found from ∼7 months to ∼2.5 years. At the annual scale, the relationships between $WD$ and all meteorological parameters were long range and no significant transition in correlation was observed showing the impact of the Earth’s annual cycle on climatic variables. All these results clearly show the influence of R-T-$Rh$-$SR$-U on $WD$ over different time scales.

1. Introduction

Nowadays, waste management is a worldwide societal issue [1,2,3,4]. In insular contexts, waste management is a main problem due to the lack of space. Open landfills are often located in the heart of agglomerations [5,6]. Apart from the nauseating odours emitted by these storage centres, the atmospheric pollutants emitted by this municipal solid waste may have a significant health impact on the neighbouring populations [7,8,9]. In a place where there are many micro-climates, it is crucial to better understand the fate of these pollutants.

In the literature, it is well known that meteorological parameters play an important role in pollutant dilution, diffusion, advection and transformation [10,11,12]. The wind is a preponderant climatic variable in these processes. Studies on wind speed behaviour are highly significant, because strong winds allow the dispersion of air pollutants in the atmospheric boundary layer, while calm winds promote its stagnation [13,14,15,16,17,18]. Nevertheless, wind direction is also a key feature as it determines the path of pollutants. In the air pollution field, the behaviour of wind direction is usually studied using statistical methods [19,20,21,22,23,24]. Although these studies provide information on the statistical behaviour of this parameter, its dynamics are not taken into account. Indeed, the results of these works are based only on a single time scale and might not necessarily reflect the features of wind direction time series over several scales [25,26]. To our knowledge, no study has yet investigated the relationship between wind direction and other meteorological parameters using the Hilbert–Huang transform (HHT) framework. For the first time, the coupled multivariate empirical mode decomposition (MEMD) [27] and time-dependent intrinsic correlation (TDIC) framework [28] are used to analyse the teleconnection between wind direction and rainfall, temperature, relative humidity, solar radiation and wind speed. The aim of this study was to analyse wind direction behaviour according to the aforementioned meteorological parameters over several time scales.

2. Materials and Methods

2.1. Study Area and Data Description

The Guadeloupe archipelago (16.25° N–61.58° W) is a French West Indies island located in the middle of the Lesser Antilles in the Caribbean basin. With an area of ∼1800 km² and a population of 390,250 inhabitants [29], this island experiences a tropical rainforest climate (“Af”) according to the Köppen–Geiger classification [30]. The study area is in the centre of Guadeloupe (Figure 1) where the topography is nearly flat and concrete buildings do not exceed four floors. The main open landfill of the island ($LF$ in Figure 1) is in the same location [31]. Embedded in a mangrove area that surrounds it, the $LF$ is sandwiched between the mangrove and a densely urbanized area [5,6]. This area is the most populated area of Guadeloupe [15].

The meteorological measurements (i.e., rainfall (R), temperature (T), relative humidity ($Rh$), solar radiation ($SR$), wind speed (U) and wind direction ($WD$)) were carried out by Météo France (https://meteofrance.gp/fr, 30 January 2023, $MF$ in Figure 1) in the study area on the international airport of Les Abymes (16.2630° N –61.61.5147° W). In order to study the relationship between $WD$ and the other meteorological parameters, a daily database was available from 2016 to 2021, i.e., 1827 points per time series. To guarantee the validity of the data, the latter were previously pre-processed by $MF$. In Figure 1, we can observe that $LF$ and $MF$ are close. Classically, the prevailing wind in the Caribbean basin comes from the east (∼90${}^{\circ }$), i.e., the trade wind. As $WD$ exhibits huge fluctuations over time due to many factors such as topography [32], the predominant $WD$ of each day was used in our analysis for a better understanding of its multi-scale behaviour.

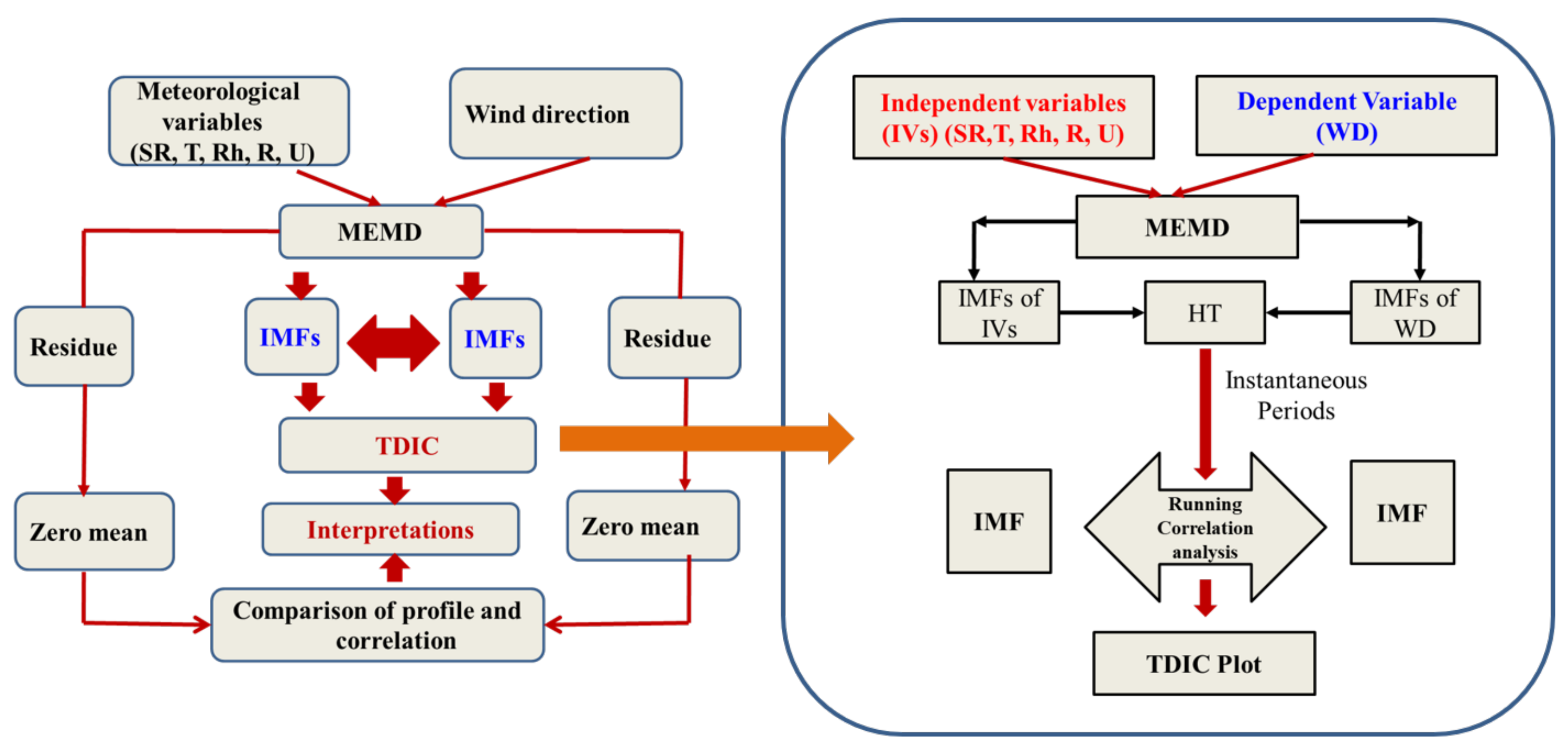
2.2. Multi-Scale Multidimensional Correlation Analysis

2.2.1. MEMD

Within 25 years of its introduction, HHT has gained wide popularity for the spectral analysis of non-linear and non-stationary time series data [33]. It is a purely data adaptive method, which can produce physically meaningful representations of time series data. This method does not require a priori selection of functions, but instead it decomposes the signal into intrinsic oscillation modes derived from the succession of extrema. The HHT involves two major steps (i), the use of the empirical mode decomposition (EMD) method or its variants, such as the ensemble EMD (EEMD), or the complete EEMD with adaptive noise (CEEMDAN) [34,35], to decompose a time series into a collection of orthogonal time series, namely, intrinsic mode functions (IMFs), and a final residue; (ii) the use of Hilbert spectral analysis (HSA) to obtain the instantaneous frequency which may be helpful to identify embedded structures of the time series data.

The EMD method decomposes a time series into a set of zero mean components and a final residue, each with specific periodicity. The decomposition is carried out based on the physical time scales that characterize the oscillations of the phenomena [36]. Different non-stationary oscillation processes controlling the variables are governed by the IMFs of the EMD [37]. In a broad sense, comparing the periodicity of the modes with that of the driving factors governs the basis of teleconnection studies [38,39]. For such studies on geophysical time series, the meteorological factors or large-scale climatic oscillations are often considered as predictors. The residue shows the long-term inherent trend of the time series and a comparison between the residue components of the variables and governing factors are likely to be well correlated [40]. The trend is an intrinsically fitted monotonic function or a function in which there can be at most one extremum within a given data span [41]. In this study, the trend represents the changes or alternations in the most likely magnitude of the wind direction throughout time.

The EMD or its variants work well for single time series data at a time and it may result in a different number of data modes adaptively, based on data complexity. This may impose difficulties in developing hybrid decomposition models [42,43] and a decomposition method, which can result in an equal number of modes being a viable option in multi-scale correlation studies, especially when multiple time series are involved. Multivariate EMD, proposed by Rehman and Mandic [27], is an extension of the traditional EMD, which decomposes multiple time series simultaneously after identifying the common scales inherent in different time series of concern. In this method, multiple envelopes are produced by taking projections of multiple inputs along different directions in an m-dimensional space.

Assuming $V\left(t\right)=\{v_1\left(t\right),v_2\left(t\right)\dots v_m\left(t\right)\}$ being the m vectors as a function of time t, and $X^{{\varphi }_k}=\{x_1^k,x_2^k,\dots ,x_m^k\}$ denoting the direction vector along different directions given by angles ${\varphi }_k=\{{\varphi }_1^k,{\varphi }_2^k,\dots ,{\varphi }_{m-1}^k\}$ in a direction set X ($k=1,2,3,\dots K$, where K is the total number of directions). It can be noted that the rotational modes appear as the counterparts of the oscillatory modes in EMD or its variants. The IMFs of m temporal datasets can be obtained by the following steps:

1.

A suitable set of direction vectors are generated by sampling on a $(m-1)$ unit hyper-sphere;

2.

The projection of the dataset $P^{{\varphi }_k}\left(t\right)$ are calculated along the direction vector $X^{{\varphi }_k}$ for all k;

3.

Temporal instants $t_i^{{\varphi }_k}$ are identified corresponding to the maxima of projection for all k;

4.

$[t_i^{{\varphi }_k},V\left(t_i^{{\varphi }_k}\right)]$ is interpolated to obtain multivariate envelope curves $e^{{\varphi }_k\left(t\right)}$ for all k;

5.

The mean of envelope curves $\left(M\right(t\left)\right)$ is calculated by $M\left(t\right)=\frac{1}{k}{\sum }_{k=1}^k{e}^{{\varphi }_k}\left(t\right)$;

6.

The “detail” $D\left(t\right)$ is extracted using $D\left(t\right)=V\left(t\right)-M\left(t\right)$. If $D\left(t\right)$ fulfils the stoppage criterion for a multivariate IMF, the above procedure from step (1) onwards is applied upon the residue series (i.e., $V\left(t\right)-D\left(t\right)$). Otherwise, steps from (2) onwards are repeated upon the series $D\left(t\right)$.

The Hammersley sampling sequence can be used for the generation of direction vectors [44] and the stoppage criteria proposed for the EMD (i.e., the sum squared difference between the deviations of the mode from the mean signal in two consecutive iterations should be less than a specified tolerance) can be used in the implementation of the MEMD.

2.2.2. HSA

In the HSA, firstly the $IMF\left(t\right)$ is convoluted with the function $g\left(t\right)=\frac{1}{\pi t}$ to obtain HT. As the function is a non-integrable one, the Cauchy principal value (PV) is considered instead of finding HT, in the following form [45]:

$$\begin{array}{cc}\hfill H\left[IMF\right(t\left)\right]& \hfill =PV{\int }_{-\infty }^{+\infty }IMF\left(\tau \right)g(t-\tau )d\tau \hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill & \hfill =\frac{1}{\pi }PV{\int }_{-\infty }^{+\infty }\frac{IMF\left(\tau \right)}{t-\tau }d\tau \hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill & \hfill =-\frac{1}{\pi }\underset{\tau \to 0}{lim}{\int }_{-\infty }^{+\infty }\frac{IMF(t+\tau )-IMF(t-\tau )}{\tau }d\tau \hfill \end{array}$$

(3)

Hence, any signal $\left(X\right(t\left)\right)$ can be represented by combining $IMF\left(t\right)$ and its HT as follows:

$$X\left(t\right)=IMF\left(t\right)+iZ\left(t\right)=A\left(t\right)e^{i\theta \left(t\right)}$$

(4)

where $i=\sqrt{-1}$, $A\left(t\right)$ is the amplitude, and $\theta \left(t\right)$ is the phase angle, which are defined as:

$$A\left(t\right)=\sqrt{IM{F}^2\left(t\right)+Z^2\left(t\right)}$$

(5)

$$\theta \left(t\right)=\frac{Z\left(t\right)}{IMF\left(t\right)}$$

(6)

In HSA, the amplitude and phase angle are both functions of time. Therefore in HSA, the plot between instantaneous frequency (IFs) and time depicting the variation of instantaneous amplitude (IAs) provide the Hilbert spectrum. IF can be computed as:

$$\omega \left(t\right)=\frac{d\theta \left(t\right)}{dt}$$

(7)

The Hilbert spectrum can be developed for individual IMFs in the form:

$$H(\omega ,t)=H[\omega \left(t\right),t]=\{A_i\left(t\right)onthecurve[\omega \left(t\right),t]:t\in R\}$$

(8)

where $i=1,2,\cdots ,N$ is the index of IMFs.

2.2.3. TDIC

In the MEMD–TDIC framework, multiple variables are decomposed into different time scales in a single step operation. It is noteworthy to mention that in TDIC, the data adaptive selection of optimal window size is followed, keeping the stationarity of the data within the window. To ensure this, the size of the sliding window is fixed based on the instantaneous period (IT) (computed by HT of IMFs). The different steps involved in the MEMD-TDIC analysis are:

1.

All time series data are decomposed using MEMD;

2.

The periodicities of the IMFs of the two time series of concern are compared and the IMFs with nearly same mean periodicity are selected;

3.

The ITs of both IMFs (of similar scale) are identified by HT;

4.

The minimum sliding window size ($t_d$) is identified as the maximum of ITs between the two signals at the current position $t_k$, i.e., $t_d=max(T_{1,i}\left(t_k\right),T_{2,i}\left(t_k\right))$;

5.

The sliding window is then fixed as $t_w^n=[t_k-\frac{n{t}_d}{2}:t_k+\frac{n{t}_d}{2}]$ where n is any positive number (a multiplication factor for minimum sliding window size). In general, n is selected as 1 [46];

6.

IMF1 and IMF2 are given as two IMFs of nearly the same mean period pertaining to two different time series. The TDIC of the pair of IMFs can be found out as $R_i\left(t_k^n\right)=Corr(IM{F}_{1,i}\left(t_w^n\right),IM{F}_{2,i}\left(t_w^n\right))$ at any $t_k$, where $Corr$ is the correlation coefficient of two time series;

7.

Student’s t-tests are performed to investigate whether the difference between the correlation coefficient $R_i\left(t_k^n\right)$ and zero is statistically significant or not;

8.

Steps 4 to 7 are repeated iteratively till the boundary of the sliding window exceeds the end points of the time series.

The end result of the TDIC analysis will be in a matrix form, based on which the TDIC plot is developed. A triangular shaped plot depicting the correlations at different time instants and under different time scales is obtained from the analysis. The bottom contour of the triangular plots depicts IFs and hence a shift of the plots to larger time scales can be noticed in higher order IMFs (i.e., of low-frequency modes). The TDIC method has gained popularity in performing multi-scale correlation analysis between teleconnected time series from different fields [32,46,47,48,49]. In this research, the HHT and TDIC methods are employed to understand the teleconnection between the hydroclimatic time series. Figure 2 shows a flowchart summarizing the complete framework of the multi-scale multidimensional correlation analysis.

3. Results and Discussion

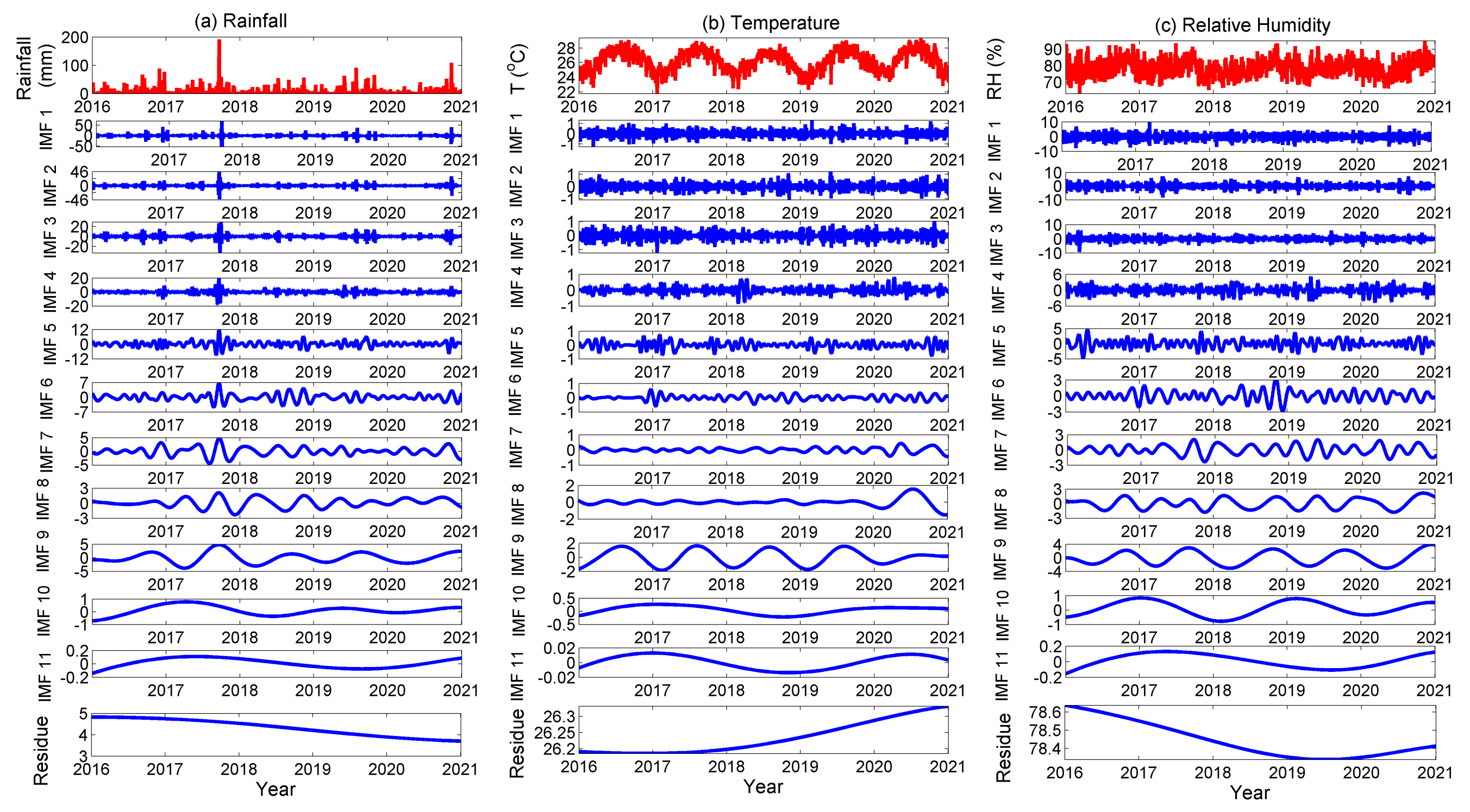
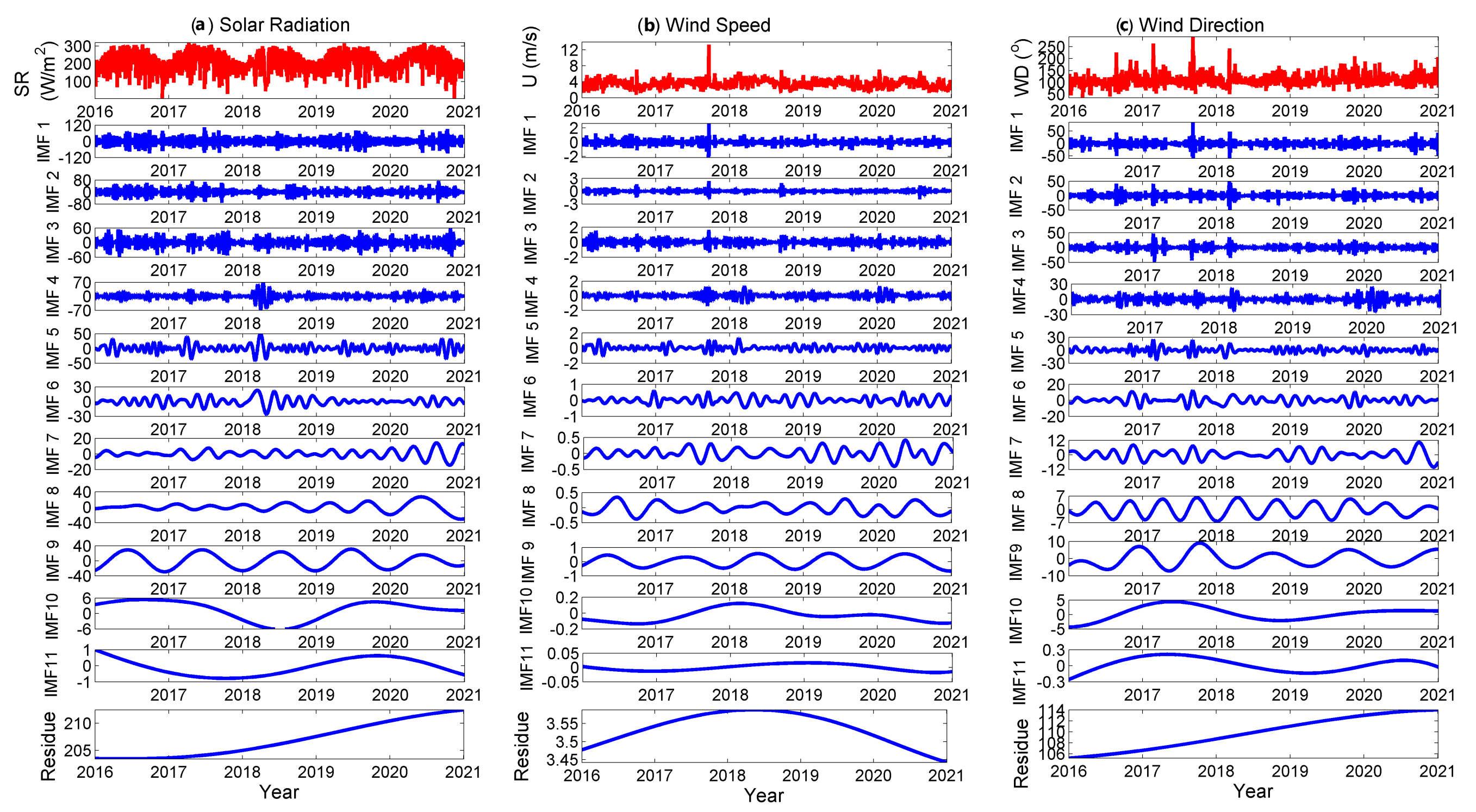
3.1. MEMD Analysis

Before performing the TDIC analysis, first we applied the multi-scale decomposition using the MEMD frameworl. In Figure 3 and Figure 4, all time series data were decomposed into 11 IMFs and one residue. The first IMF mode represents the fast fluctuations, while the last mode represents the slowest fluctuations, i.e., an increase in the time scale with the mode index [50,51]. At first glance, we can notice that some residues, i.e., the overall trend of the time series, seem to exhibit the same behaviour over time: a decrease for R-$Rh$, an increase for T-$SR$-$WD$ and a mixture of both for U. The amplitude of these residues vary on small ranges showing that the changes in climatic regimes from one year to the next are not significant [52].

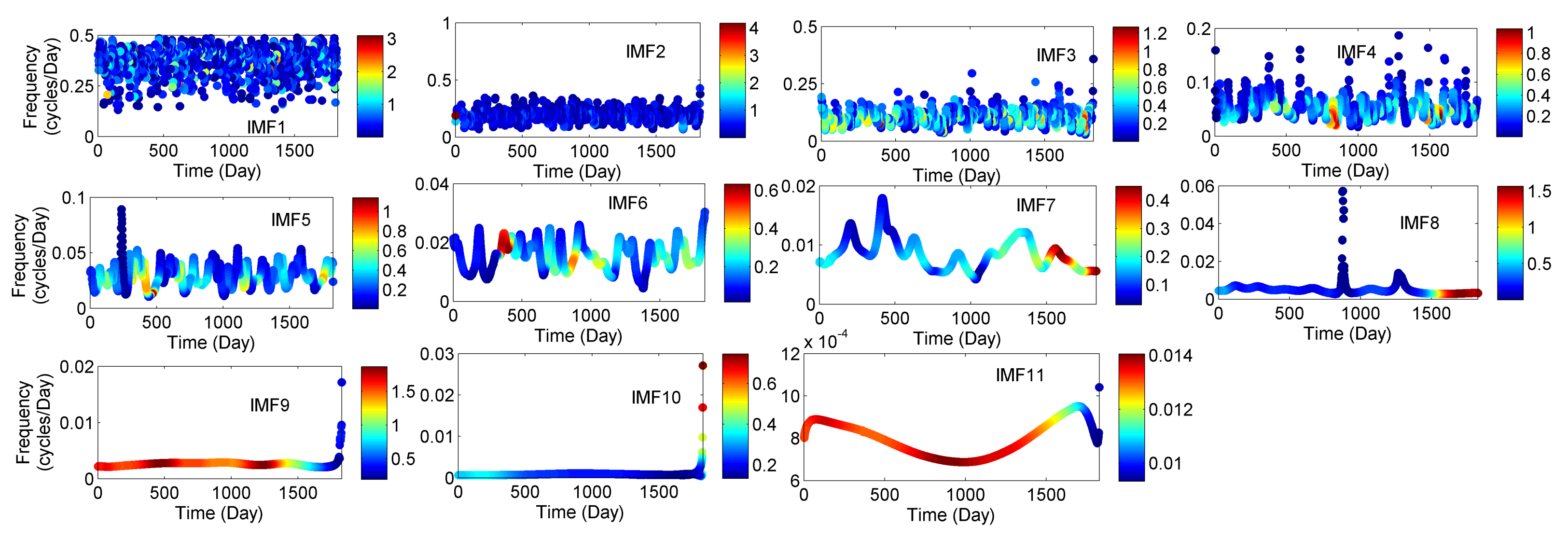
3.2. Instantaneous Frequency of Meteorological Parameters (IMFs)

To quantitatively determine the physical meaning behind the MEMD method and compare the IMFs, the mean periodicity of each IMF and their variability are presented in

Table 1. Periodicity ($\overline{T}$) and variability (V) obtained by the MEMD analysis for all parameters. LT is for long term.

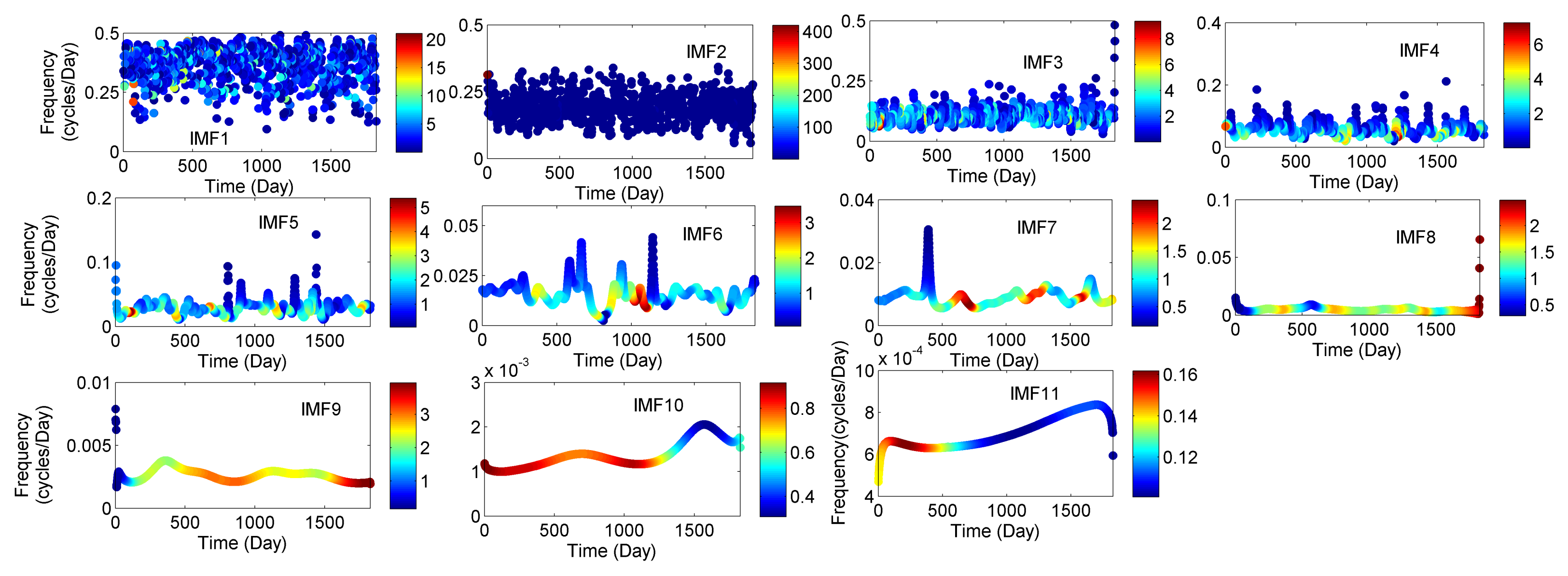
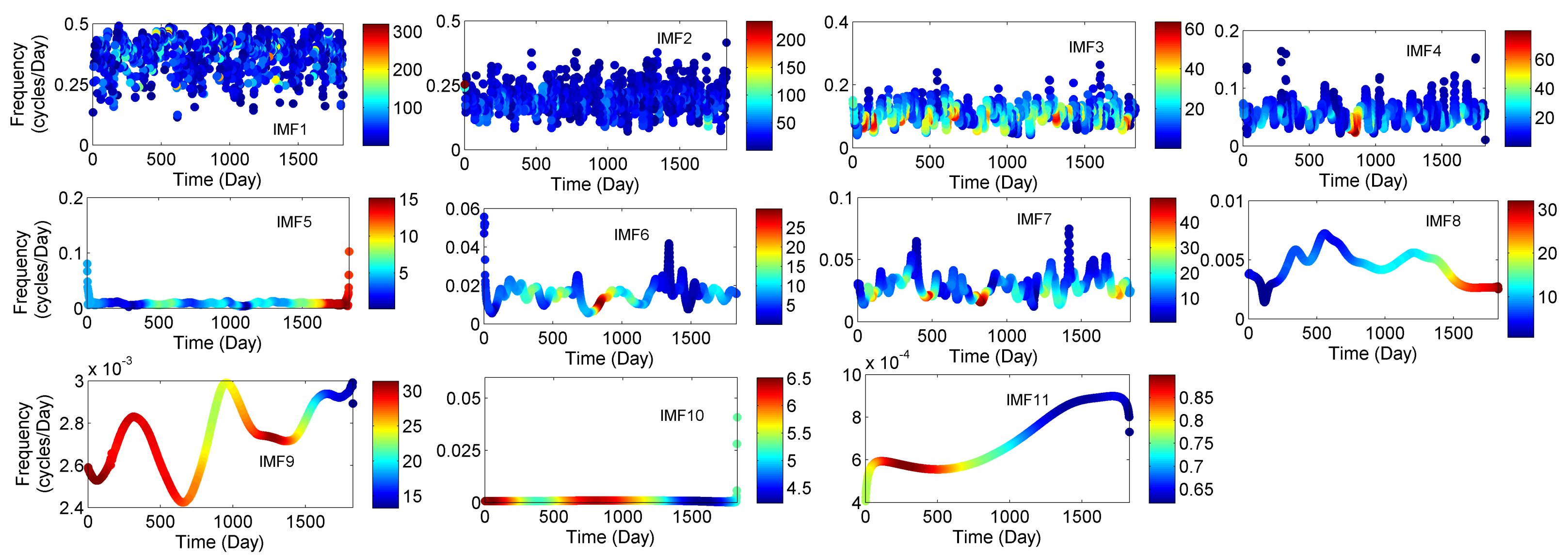
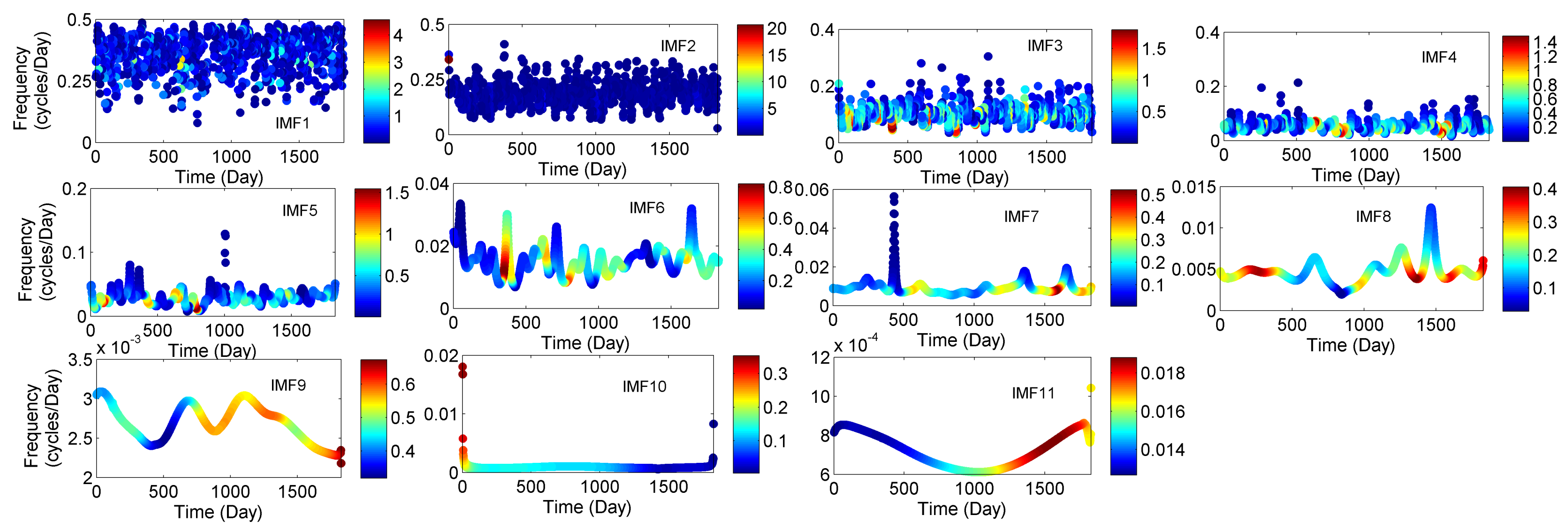
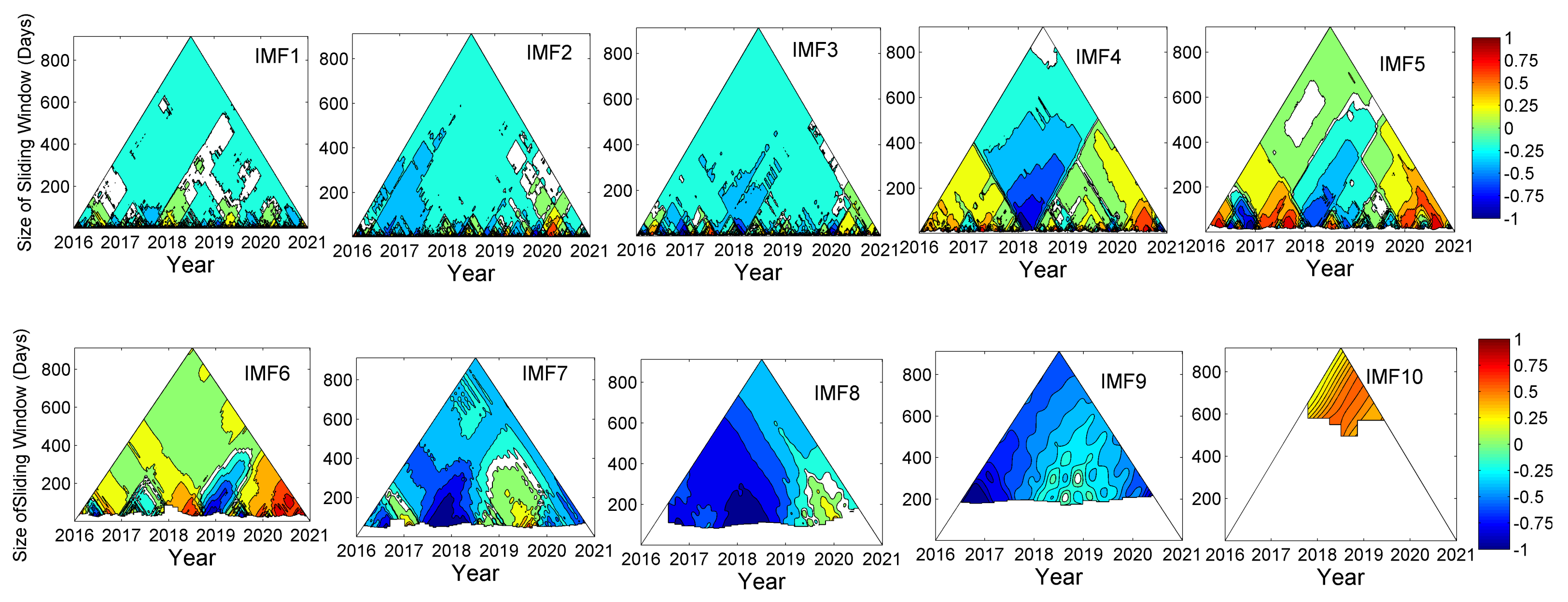
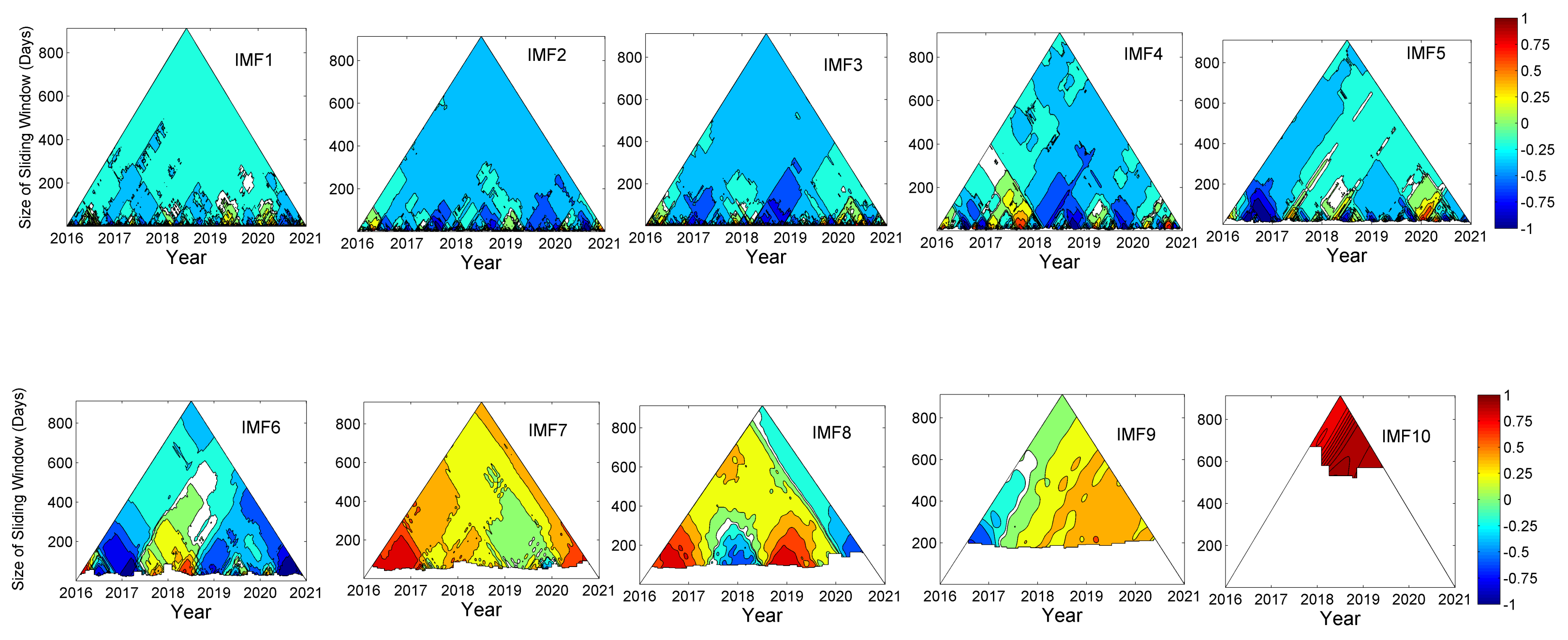
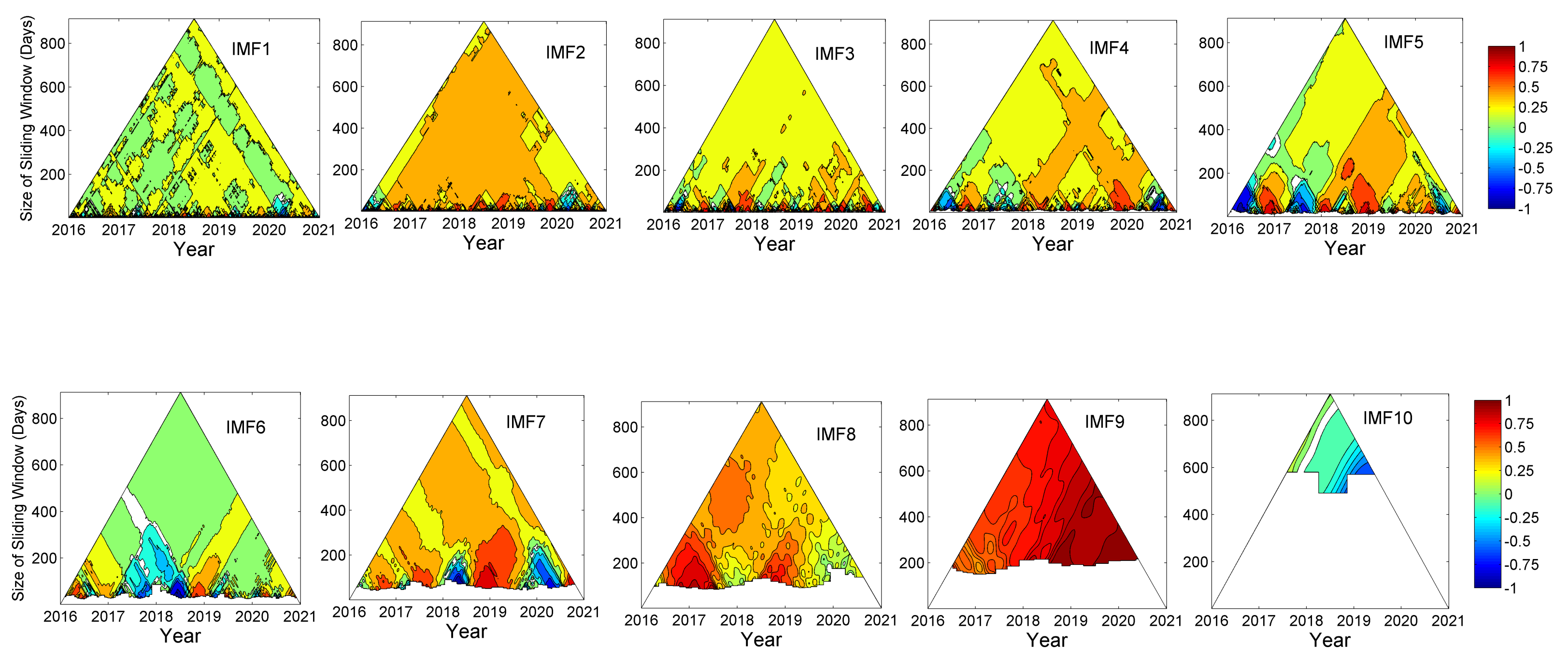
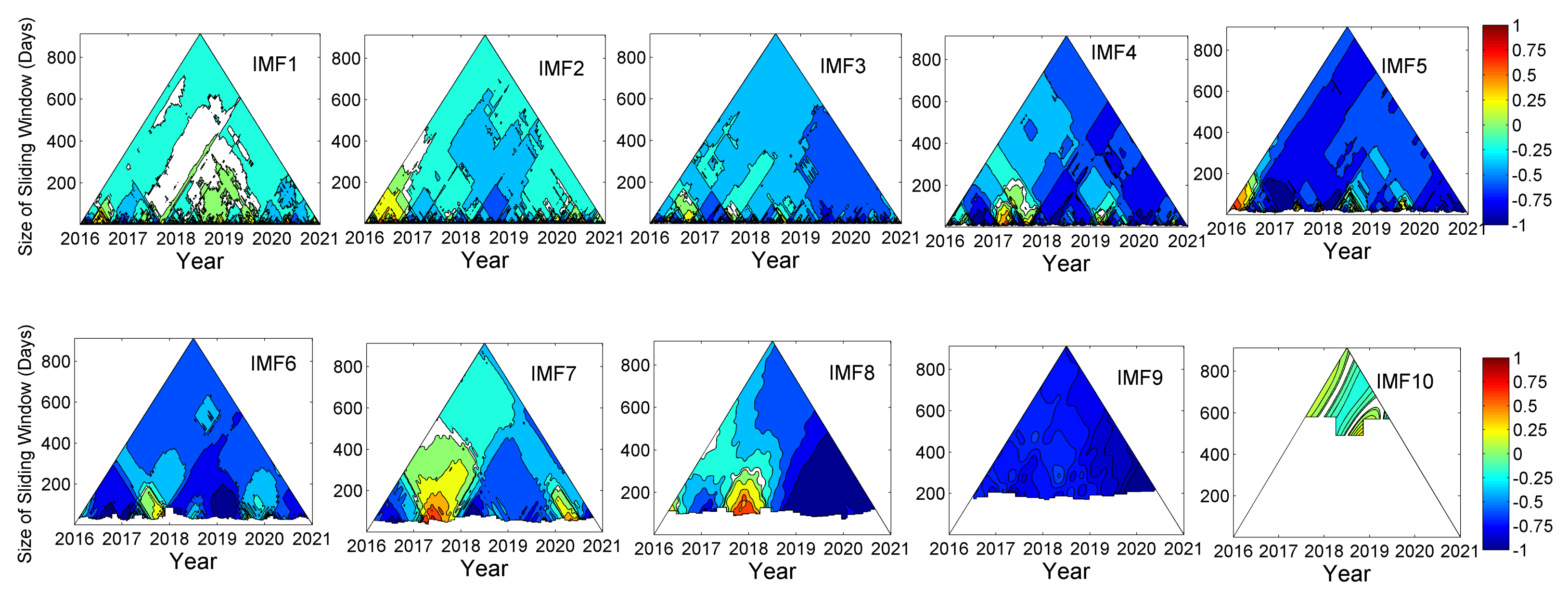
	Rainfall		Temperature		Relative Humidity
Modes	$\overline{\mathit{T}}$(Days)	V (%)	$\overline{\mathit{T}}$(Days)	V (%)	$\overline{\mathit{T}}$(Days)	V (%)
IMF1	2.905	38.974	2.671	5.536	2.687	19.992
IMF2	4.885	20.720	4.872	5.000	4.978	16.638
IMF3	8.742	17.364	8.659	5.550	8.659	13.764
IMF4	16.459	8.236	15.887	2.911	16.917	9.980
IMF5	31.500	5.265	31.500	3.656	33.218	8.820
IMF6	60.900	2.547	57.094	1.584	60.900	3.796
IMF7	101.500	2.202	114.188	1.259	114.188	4.085
IMF8	203.000	0.776	203.000	12.268	203.000	5.074
IMF9	304.500	3.633	365.400	60.834	304.500	16.740
IMF10	609.000	0.130	913.500	1.260	609.000	1.039
IMF11	1827.000	0.004	913.500	0.005	1827.000	0.031
Residue	LT	0.150	LT	0.139	LT	0.041
	Solar radiation		Wind speed		Wind direction
Modes	$\overline{T}$ (Days)	V (%)	$\overline{T}$ (Days)	V (%)	$\overline{T}$ (Days)	V (%)
IMF1	2.687	31.998	2.659	13.060	2.699	29.116
IMF2	4.885	15.998	4.911	14.761	4.885	18.601
IMF3	8.869	12.871	8.659	17.381	8.659	17.494
IMF4	17.075	9.077	16.761	15.065	16.917	10.567
IMF5	34.472	7.192	32.053	13.015	32.625	8.337
IMF6	60.900	2.249	63.000	5.008	60.900	3.432
IMF7	107.471	0.941	107.471	2.962	101.500	3.068
IMF8	228.375	4.901	203.000	3.214	182.700	2.666
IMF9	365.400	13.829	365.400	14.635	365.400	3.752
IMF10	913.500	0.547	913.500	0.685	913.500	1.121
IMF11	1827.000	0.011	1827.000	0.014	913.500	0.003
Residue	LT	0.388	1827.000	0.200	LT	1.842

for all parameters. The mean period is computed by the zero crossing method [34]. The ratio of variance of a mode (IMF or residue) to the variance of the data series (expressed in %) is computed as variability (V). Overall, the variability seems to decrease with increasing time scales. At IMF9, we notice a sudden increase in the variability. This may due to the impact of the Earth’s annual cycle [53] on different meteorological parameters.

Then, HHT is applied for each IMF of all the variables and IFs and IAs are computed. The instantaneous frequency trajectories associated with the IMFs of different variables are presented in different panels of time-frequency-amplitude (TFA) spectra shown in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10. In the TFA spectra, the colour scale indicates the distribution of amplitude (in respective units). In general, the high amplitudes are noticed at very localized time instants in high-frequency IMFs (up to weekly scale) to seasonal time scales of ∼4 months (IMF7). The components of intra-seasonal to inter-annual periodicity are affected significantly by high amplitude. The high amplitudes are present for a longer time in the TF spectra of the IMFs of larger time scales of intra-seasonal periodicity. However, such spells pertaining to different variables do not need to be at the same time instants, indicating that the dominant contributor to the $WD$ variability at different time spells may be different. Strong singularities in the form of abrupt changes in the IFs are noted in the TFA spectra of different variables in the monthly to seasonal time scales (IMF5 to IMF7). However, the period of occurrence of such abrupt shifts is also noted at different time instants, even though one of such a shift around the year of 2018 is evident, in line with the peaks in the time series of variables such as rainfall, relative humidity, wind speed and wind direction.

In the study, three types of correlation analysis were performed (i), Pearson’s correlation between the raw time series of meteorological variables with $WD$ (ii), Pearson’s correlation between the modes of variables and modes of $WD$ series (iii), running correlation between the modes of variables and modes of $WD$ series at different scales. The overall correlation between $WD$ and the parameters are presented in

Table 2. Pearson’s correlation coefficients of the raw time series between wind direction ($WD$) and rainfall (R), temperature (T), relative humidity ($Rh$), solar radiation ($SR$) and wind speed (U).

Parameters	Pearson Correlation
$WD$ vs. R	0.11
$WD$ vs. T	−0.04
$WD$ vs. $Rh$	0.32
$WD$ vs. $SR$	−0.08
$WD$ vs. U	−0.29

. One can notice that the correlations are not significant in any of the cases.

To gain better insights into the association between meteorological variables and $WD$ at different time scales, Pearson’s correlations between the modes of variables and that of $WD$ are computed and presented in

Table 3. Correlation between the modes of wind direction and the modes of rainfall, temperature, relative humidity, solar radiation and wind speed. Significant correlations at the 5% level are marked in bold.

	Rainfall
Wind Direction	IMF1	IMF2	IMF3	IMF4	IMF5	IMF6	IMF7	IMF8	IMF9	IMF10	IMF11	Residue
IMF1	0.085	−0.003	−0.009	0.003	−0.009	−0.008	−0.015	−0.003	−0.006	−0.005	−0.004	0.006
IMF2	−0.004	0.166	0.023	−0.004	−0.006	0.006	−0.001	0.011	−0.003	−0.003	−0.001	0.002
IMF3	−0.008	0.004	0.101	0.021	0.000	−0.015	−0.006	−0.001	−0.007	−0.004	−0.005	0.010
IMF4	0.003	0.000	−0.016	−0.050	0.040	0.003	0.004	−0.003	−0.016	−0.017	−0.011	−0.019
IMF5	0.012	−0.015	0.016	−0.007	−0.050	0.047	0.010	0.022	0.002	0.017	0.000	0.006
IMF6	−0.009	−0.020	0.021	0.015	−0.045	0.023	0.038	0.045	−0.002	−0.020	−0.019	0.007
IMF7	−0.010	−0.007	−0.019	−0.008	−0.016	0.009	0.288	0.054	−0.066	0.031	0.044	−0.008
IMF8	−0.004	−0.006	−0.007	0.007	0.028	0.056	0.178	0.690	−0.104	0.036	0.041	0.144
IMF9	−0.038	0.004	0.000	0.009	0.016	0.031	−0.071	−0.006	0.744	0.115	0.038	0.056
IMF10	−0.018	−0.002	0.009	0.003	0.007	0.026	−0.024	0.014	0.233	0.816	0.664	−0.014
IMF11	−0.018	−0.001	0.012	−0.002	0.001	−0.002	−0.051	−0.004	0.184	0.765	0.880	−0.318
Residue	0.004	−0.005	−0.015	0.015	0.007	−0.004	0.048	−0.047	−0.097	−0.007	0.228	−0.993
Wind direction	Temperature
IMF1	−0.153	0.012	0.020	−0.027	0.008	0.011	0.023	0.011	−0.002	0.012	0.009	0.008
IMF2	0.003	−0.204	−0.057	0.000	0.005	−0.008	0.012	−0.013	0.005	−0.007	−0.009	0.012
IMF3	0.020	−0.039	−0.228	−0.045	−0.009	−0.005	0.017	−0.001	−0.002	0.000	−0.001	0.003
IMF4	0.002	0.011	−0.006	−0.186	−0.008	0.030	0.015	−0.004	−0.001	0.015	0.019	0.015
IMF5	0.013	0.015	−0.001	−0.074	−0.188	0.007	0.018	−0.002	0.004	−0.018	−0.005	−0.027
IMF6	0.006	−0.005	0.004	0.002	0.059	−0.245	−0.078	0.046	−0.027	0.023	0.016	−0.005
IMF7	0.003	−0.004	0.003	0.003	0.019	−0.022	0.505	0.088	0.003	−0.019	−0.002	−0.007
IMF8	0.020	−0.002	0.002	0.013	0.018	−0.004	0.171	−0.059	−0.225	0.038	0.134	0.044
IMF9	−0.019	0.001	0.003	−0.008	0.022	0.080	−0.039	−0.023	0.117	−0.004	0.028	0.001
IMF10	−0.012	−0.005	−0.002	−0.016	0.009	0.036	−0.018	0.001	0.134	0.776	0.780	−0.162
IMF11	−0.005	−0.007	−0.007	−0.016	0.010	0.048	−0.003	−0.026	0.028	0.630	0.721	−0.147
Residue	−0.003	0.002	0.010	−0.013	−0.004	0.015	−0.054	0.031	0.076	0.002	−0.197	0.941
Wind direction	Relative humidity
IMF1	0.199	−0.004	−0.008	0.014	−0.007	0.005	−0.021	0.004	0.005	−0.012	−0.011	0.002
IMF2	0.014	0.386	0.057	−0.004	−0.001	0.002	−0.004	0.012	−0.004	0.002	0.000	0.003
IMF3	−0.016	0.041	0.304	0.063	−0.009	−0.004	0.007	0.018	−0.007	0.002	0.002	0.012
IMF4	0.000	−0.006	0.029	0.345	0.081	−0.007	−0.016	0.014	0.002	−0.021	−0.013	−0.029
IMF5	0.007	−0.013	0.012	0.045	0.200	0.088	0.004	0.016	0.009	0.017	0.004	0.019
IMF6	0.007	−0.004	0.005	0.009	−0.012	0.151	0.155	0.017	0.010	0.017	0.015	−0.003
IMF7	−0.013	−0.004	−0.012	−0.008	0.001	0.011	0.454	0.084	−0.063	−0.001	0.016	−0.017
IMF8	−0.004	−0.003	−0.013	0.007	0.003	0.007	0.055	0.398	0.123	0.003	−0.061	0.119
IMF9	−0.033	0.001	0.001	0.011	0.015	0.039	−0.068	0.030	0.760	0.111	0.015	0.093
IMF10	−0.004	−0.010	0.001	0.017	0.007	0.075	−0.011	−0.014	0.042	0.107	0.022	0.010
IMF11	−0.017	−0.003	0.009	−0.002	0.002	0.003	−0.051	−0.016	0.165	0.753	0.889	−0.309
Residue	0.003	−0.010	−0.025	0.015	0.012	0.023	0.020	−0.073	−0.119	0.001	0.271	−0.894
Wind direction	Solar radiation
IMF1	−0.056	−0.002	0.014	−0.012	0.006	0.008	0.007	0.001	0.007	0.006	0.008	−0.010
IMF2	0.007	−0.128	−0.026	0.003	0.001	−0.006	−0.009	−0.008	0.001	−0.004	−0.002	−0.007
IMF3	0.003	−0.008	−0.093	0.002	−0.006	0.000	0.004	−0.004	0.002	0.013	0.013	−0.002
IMF4	0.002	0.007	0.004	−0.015	−0.005	0.005	−0.003	−0.008	0.013	0.009	0.003	0.006
IMF5	−0.002	−0.001	−0.022	0.051	0.152	0.008	0.004	0.017	−0.023	−0.006	0.006	−0.018
IMF6	0.006	0.010	−0.009	−0.016	0.059	0.202	−0.071	0.026	−0.043	−0.001	0.009	0.000
IMF7	0.007	−0.002	0.005	0.018	−0.001	−0.031	−0.349	−0.144	0.023	−0.010	−0.018	0.007
IMF8	0.013	0.005	0.005	−0.010	0.010	−0.049	0.048	−0.270	−0.261	0.000	0.089	−0.047
IMF9	0.005	−0.001	−0.002	−0.005	0.015	0.066	−0.004	−0.030	−0.533	−0.047	−0.008	−0.063
IMF10	0.000	−0.008	−0.020	−0.002	0.014	0.051	0.007	−0.014	−0.015	0.215	0.171	−0.203
IMF11	0.017	−0.002	−0.017	−0.002	0.003	0.026	0.048	−0.003	−0.183	−0.612	−0.707	0.254
Residue	−0.004	0.004	0.013	−0.014	−0.006	0.008	−0.050	0.040	0.087	−0.003	−0.224	0.977
Wind direction	Wind speed
IMF1	−0.085	0.012	0.007	−0.025	0.001	0.012	0.002	0.011	−0.010	0.008	0.013	0.004
IMF2	0.000	−0.096	−0.066	−0.002	0.002	−0.009	0.000	−0.006	0.005	0.009	0.010	−0.006
IMF3	0.021	−0.035	−0.294	−0.058	−0.030	−0.014	0.000	−0.014	−0.010	−0.015	−0.014	−0.004
IMF4	−0.006	0.011	−0.012	−0.465	−0.014	0.039	0.024	−0.009	−0.018	0.013	0.011	0.011
IMF5	0.005	0.000	0.010	−0.098	−0.489	−0.065	−0.002	0.002	0.009	−0.018	−0.018	−0.019
IMF6	−0.003	−0.009	0.016	0.019	−0.061	−0.480	−0.093	−0.066	−0.011	−0.001	−0.009	0.002
IMF7	0.003	0.001	−0.006	0.018	−0.026	−0.097	−0.265	−0.076	−0.022	0.031	0.015	0.020
IMF8	0.001	−0.002	0.001	−0.008	−0.035	−0.006	−0.039	−0.383	−0.111	0.026	0.084	−0.080
IMF9	0.022	0.000	−0.006	−0.011	−0.004	0.042	0.041	−0.003	−0.749	−0.104	−0.029	−0.060
IMF10	−0.003	0.014	0.018	−0.008	−0.013	−0.086	0.012	0.049	0.083	0.065	0.023	0.059
IMF11	0.007	0.009	0.010	0.008	−0.010	−0.044	0.027	0.048	−0.025	−0.532	−0.675	0.157
Residue	−0.001	0.008	0.018	−0.001	−0.009	−0.047	0.046	0.042	0.055	0.089	0.056	−0.256

. In Table 3, the significant correlations between $WD$ and the other meteorological parameters (R-T-$Rh$-$SR$-U) are from IMF7 to IMF11, i.e., for large time scales. Unlike the other parameters, there is no significant correlation for the residual between U and $WD$. This seems to show that $WD$ is less dependent on U for the overall trend. The micro-climate of this area will therefore have a major impact on $WD$ behaviour. Indeed, since the study area is in the continental island regime of the island, the trade winds speed (U) will be highly dependent on thermal convection during the day and ground cooling during the night. Consequently, $WD$ behaviour will be also strongly impacted [54].

3.3. TDIC Analysis

The Pearson’s correlations between the modes of meteorological variables and $WD$ showed that high correlations are noted only at low-frequency modes. However, it is worth mentioning that in the computation of the overall correlation between the modes, the complete data length is considered. The reasons behind low correlation between the modes in the high-frequency scale must be investigated in detail. However, in the process of the complex behaviour of $WD$ controlled by many local meteorological variables, one cannot conclude that the same low-magnitude correlation will be preserved over the complete period of observation. On the other hand, the correlation may be very strong (positive or negative) at some of the localized time spells and very weak in some other spells in some of the time scales. The effect of positive correlation in some time spells might be nullified because of the negative correlation with other spells. Moreover, it is found that the overall correlation of the different variables with $WD$ is very small (Table 2). Furthermore, even if the overall correlation in some scales is strongly positive (or negative), its influence will be cancelled due to strong negative (or positive) correlations at other scales, leading to an overall low correlation between the raw time series. Therefore, it is very important to find the localized correlations, for which a running correlation method should be used. Therefore, to analyse the localized correlations between $WD$ and $SR$-T-$Rh$-R-U over time, a TDIC analysis was performed. The TDIC analysis creates a graphic triangle, where the vertical axis is the sliding window size and the horizontal axis represents the centre position of the sliding window. The minimum size of the sliding window is the maximum instantaneous period between $WD$ and the other meteorological parameters, whereas the maximum window size is the entire time range [55]. The colour bar indicates the correlation intensity between the studied variables, i.e., red and blue highlight the positive and negative correlations, respectively. White regions in the triangle indicate statistical insignificance when the correlations do not pass the Student’s t-test. Hence, the correlation is not statistically significant [28].

Overall, fom Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15, one can notice there were localized positive and negative correlations between $WD$ and the meteorological parameters from IMF1 (∼3 days) to IMF8 (∼7 months). The transitions in the correlation are more frequent with T and $Rh$ (Figure 12 and Figure 13), implying that the local meteorology may have a strong interaction with these variables to determine $WD$ behaviour. This can be explained by the impact of the urban heat island (UHI) previously identified in the study area by Plocoste et al. [54] which generates an urban breeze in the evening allowing the transportation of volatile organic compounds (VOCs) emitted by LF to the urban areas opposite to the flow of the trade winds, i.e., to the west [31,54]. This urban breeze may explain the dominance of negative associations between $WD$ and U in Figure 15. During this event, the UHI can reach 6 °C and generate a breeze of 1 m/s [54]. The cold and moist air coming from the mangrove will be loaded with air pollutants while passing over the LF and then cool T of the contiguous urban areas. The authors assume that this will also increase the humidity of these areas.

In Figure 11, there is also a dominance of negative correlation between $WD$ and $SR$. This may be due to the impact of the diurnal cycle on the atmospheric boundary layer behaviour [56]. During the day, the mixed layer is at its maximum height, allowing the trade wind to establish itself in the study area. In the evening, the radiative cooling of the ground pushes the trade wind above the nocturnal boundary layer allowing the establishment of the urban breeze in the surface layer, thus changing $WD$ behaviour.

From Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15, the relationships are long range, consistent and no transition in the correlation was noticed at IMF9, i.e., annual scale. These results dynamically show the impact of the Earth’s annual cycle [53] which tends to homogenize the interactions between the meteorological parameters. IMF8 (∼7 months) to IMF10 (∼2.5 years) in Figure 14, R display a strong positive correlation with the IMFs of $WD$. R is the only variable that shows a strong positive correlation with $WD$ on three consecutive time scales. As heavy rains and cyclones can cause micro-bursts that modify $WD$ behaviour [57], we assume that these three large scales may correspond to periods without extreme rainy events.

The multi-scale correlation analysis can be considered as one of the potential pre-requisites for developing hybrid decomposition machine learning models for the prediction of complex time series. In such a framework, the dominant predictors in different time scales can be identified using TDIC-based multi-scale correlation analysis. Thereafter predictions can be carried out for individual scales separately and final integration will provide the prediction of wind direction. The framework is well-described and applied for the prediction of geophysical series [43,50,58]. Thus, the study has great potential for improving the predictability of wind direction, hence modelling the transportation of air pollutants.

4. Conclusions

Wind direction is a key parameter during pollutant transportation. In insular contexts, there is a wide variety of meteorological contexts due to micro-climates. For the first time in the literature, the coupled MEMD–TDIC has been used to study the dynamical relationship between wind direction ($WD$) and other meteorological parameters (rainfall (R), temperature (T), relative humidity ($Rh$), solar radiation ($SR$) and wind speed (U)) in a multi-scale way.

Overall, localized positive and negative correlations between $WD$ and the meteorological parameters were identified from ∼3 days to ∼7 months. The alternation between these correlations were more significant for T and $Rh$. For $SR$ and U, there is a dominance of a negative correlation with $WD$. We believe that the local micro-climate specific to the study area may explain all these behaviours. From ∼7 months to ∼2.5 years, there is a strong positive correlation between $WD$ and R. We assume that these time scales correspond to a period without extreme rainy events. It is important to underline that at the annual scale, the relationships are of long range, consistent and no significant transition in correlation was found between $WD$ and all the meteorological parameters. This time scale shows the influence of the Earth’s annual cycle on the behaviour of meteorological parameters.

The results obtained in this study clearly show the impact of R-T-$Rh$-$SR$-U on $WD$ over different time scales. Due to the small size of the Caribbean islands, these results are crucial because they provide information on the impact of micro-climates on $WD$ behaviour. In order to develop predictive models for $WD$, the lagged influence of correlations also needs to be studied. This will be the subject of our next study using the time-dependent intrinsic cross correlation (TDICC) framework.