Assessing Climate Change Impact on Rainfall Patterns in Northeastern India and Its Consequences on Water Resources and Rainfed Agriculture
Abstract
:1. Introduction
2. Materials and Methods
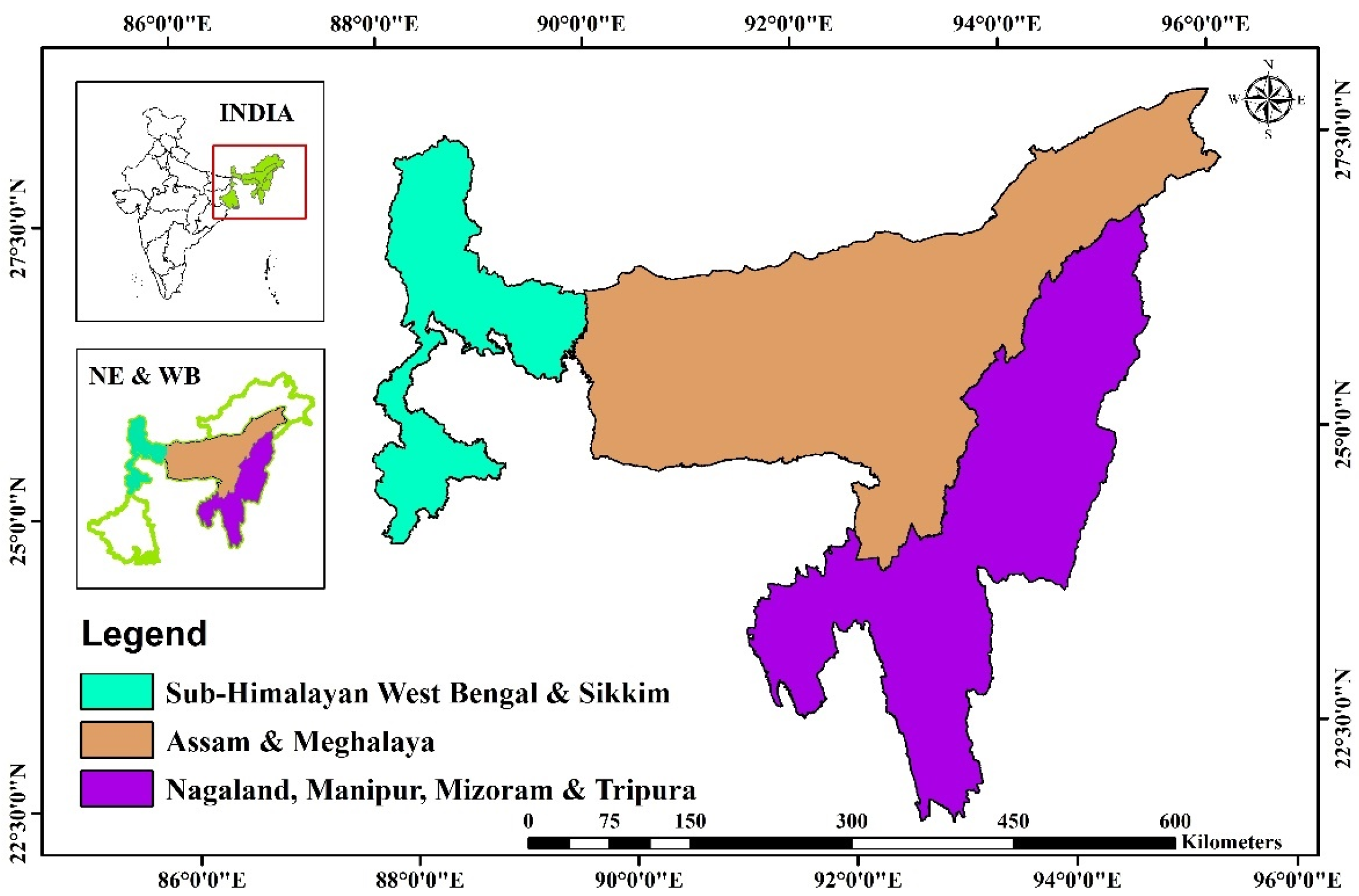
2.1. Study Area
2.2. Data Source
2.3. Data Analysis
2.3.1. Methods for Trend Analysis
2.3.2. Mann–Kendall Test
2.3.3. Sen’s Slope Estimator
2.3.4. Spearman’s Rho Tests (SRHO)
2.3.5. Ordinary Least Square (OLS) Linear Regression
2.3.6. Innovative Trend Analysis
2.3.7. Change Point Analysis Techniques
2.3.8. Pettitt Test
2.3.9. Standard Normal Homogeneity Test
2.3.10. Buishand Range Test
3. Results and Discussion
3.1. Summary Statistics of the Rainfall Data
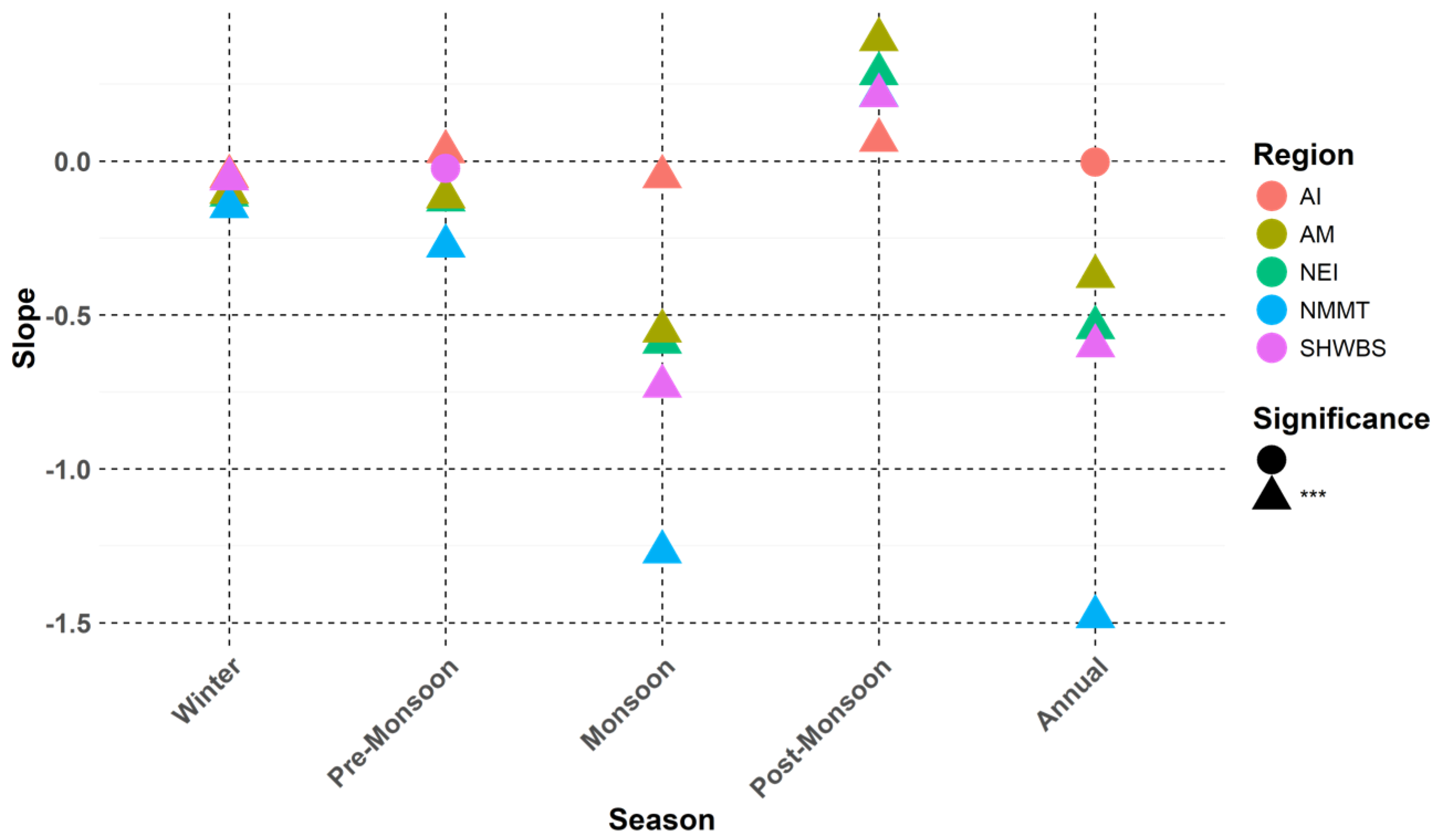
3.2. Trend in the Rainfall Time Series Data
3.3. Innovative Trend Analysis of the Rainfall Time Series Data
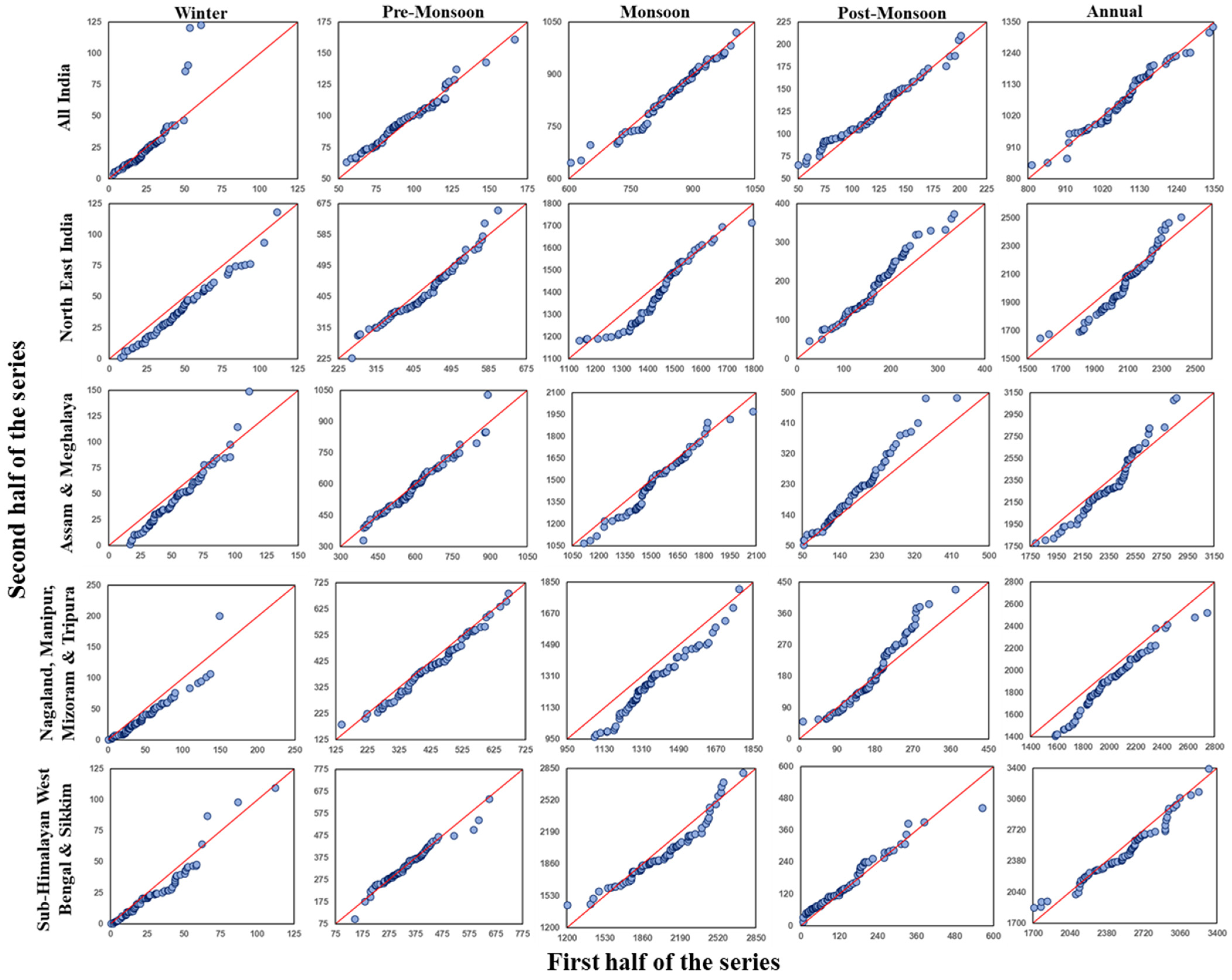
3.4. Changes in Mean, Variability, and Probability Distribution
3.5. Change Point Analysis of the Rainfall Time Series Data
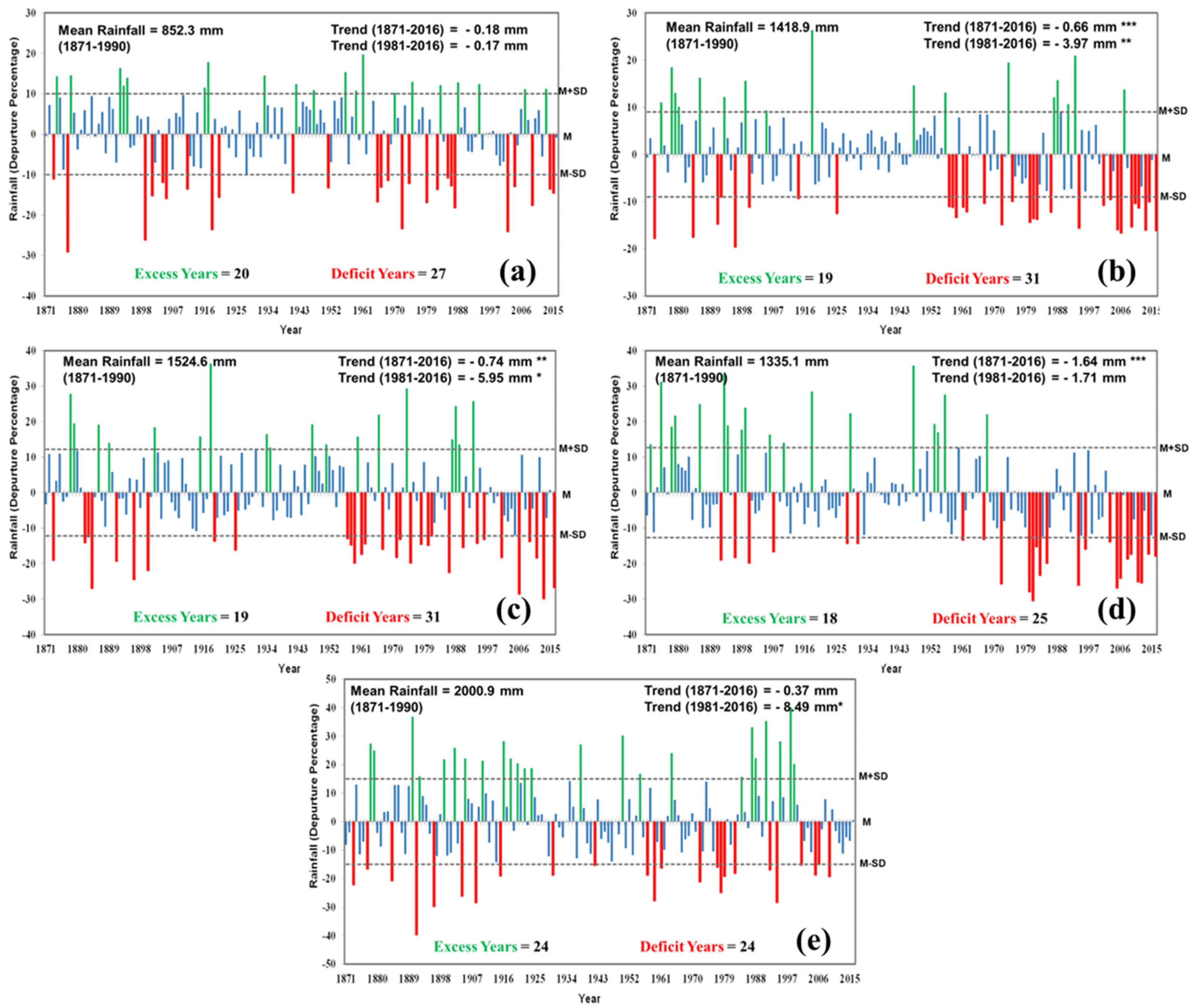
3.6. Trends and Variability in Rainfall Anomalies During the Monsoon Season
3.7. Change in the Return Periods of Assured Rainfall
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Intergovernmental Panel on Climate Change (IPCC). Summary for Policymakers. In Climate Change 2021—The Physical Science Basis: Working Group I Contribution to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2023; pp. 3–32. [Google Scholar] [CrossRef]
- Pecl, G.T.; Araújo, M.B.; Bell, J.D.; Blanchard, J.; Bonebrake, T.C.; Chen, I.-C.; Clark, T.D.; Colwell, R.K.; Danielsen, F.; Evengård, B. Biodiversity Redistribution under Climate Change: Impacts on Ecosystems and Human Well-Being. Science 2017, 355, eaai9214. [Google Scholar] [CrossRef] [PubMed]
- Huang, M.-T.; Zhai, P.-M. Achieving Paris Agreement Temperature Goals Requires Carbon Neutrality by Middle Century with Far-Reaching Transitions in the Whole Society. Adv. Clim. Chang. Res. 2021, 12, 281–286. [Google Scholar] [CrossRef]
- Li, D.; Wu, S.; Liu, L.; Zhang, Y.; Li, S. Vulnerability of the Global Terrestrial Ecosystems to Climate Change. Glob. Chang. Biol. 2018, 24, 4095–4106. [Google Scholar] [CrossRef]
- Awasthi, N.; Tripathi, J.N.; Petropoulos, G.P.; Kumar, P.; Singh, A.K.; Dakhore, K.K.; Ghosh, K.; Gupta, D.K.; Srivastava, P.K.; Kalogeropoulos, K. Long-Term Spatiotemporal Investigation of Various Rainfall Intensities over Central India Using EO Datasets. Hydrology 2024, 11, 27. [Google Scholar] [CrossRef]
- Dore, M.H.I. Climate Change and Changes in Global Precipitation Patterns: What Do We Know? Environ. Int. 2005, 31, 1167–1181. [Google Scholar] [CrossRef] [PubMed]
- Trenberth, K.E. Changes in Precipitation with Climate Change. Clim. Res. 2011, 47, 123–138. [Google Scholar] [CrossRef]
- Nielsen, U.N.; Ball, B.A. Impacts of Altered Precipitation Regimes on Soil Communities and Biogeochemistry in Arid and Semi-arid Ecosystems. Glob. Chang. Biol. 2015, 21, 1407–1421. [Google Scholar] [CrossRef]
- Sun, F.; Roderick, M.L.; Farquhar, G.D. Rainfall Statistics, Stationarity, and Climate Change. Proc. Natl. Acad. Sci. USA 2018, 115, 2305–2310. [Google Scholar] [CrossRef]
- Gründemann, G.J.; van de Giesen, N.; Brunner, L.; van der Ent, R. Rarest Rainfall Events Will See the Greatest Relative Increase in Magnitude under Future Climate Change. Commun. Earth Environ. 2022, 3, 235. [Google Scholar] [CrossRef]
- Korner, C.; Spehn, E.M. Mountain Biodiversity: A Global Assessment; CRC Press: Routledge, UK, 2019; Volume 7, ISBN 1000698297. [Google Scholar]
- Peters, M.K.; Hemp, A.; Appelhans, T.; Becker, J.N.; Behler, C.; Classen, A.; Detsch, F.; Ensslin, A.; Ferger, S.W.; Frederiksen, S.B. Climate–Land-Use Interactions Shape Tropical Mountain Biodiversity and Ecosystem Functions. Nature 2019, 568, 88–92. [Google Scholar] [CrossRef] [PubMed]
- Schmeller, D.S.; Urbach, D.; Bates, K.; Catalan, J.; Cogălniceanu, D.; Fisher, M.C.; Friesen, J.; Füreder, L.; Gaube, V.; Haver, M. Scientists’ Warning of Threats to Mountains. Sci. Total Environ. 2022, 853, 158611. [Google Scholar] [CrossRef] [PubMed]
- Sambieni, K.S.; Hountondji, F.C.C.; Sintondji, L.O.; Fohrer, N.; Biaou, S.; Sossa, C.L.G. Climate and Land Use/Land Cover Changes within the Sota Catchment (Benin, West Africa). Hydrology 2024, 11, 30. [Google Scholar] [CrossRef]
- Achite, M.; Caloiero, T.; Wałęga, A.; Ceppi, A.; Bouharira, A. Trend Analysis of Hydro-Meteorological Variables in the Wadi Ouahrane Basin, Algeria. Hydrology 2024, 11, 77. [Google Scholar] [CrossRef]
- Rashiq, A.; Kumar, V.; Prakash, O. A Spatiotemporal Assessment of the Precipitation Variability and Pattern and an Evaluation of the Predictive Reliability of Global Climate Models over Bihar. Hydrology 2024, 11, 50. [Google Scholar] [CrossRef]
- Drenkhan, F.; Buytaert, W.; Mackay, J.D.; Barrand, N.E.; Hannah, D.M.; Huggel, C. Looking beyond Glaciers to Understand Mountain Water Security. Nat. Sustain. 2023, 6, 130–138. [Google Scholar] [CrossRef]
- Fan, L.; Kuang, X.; Or, D.; Zheng, C. Streamflow Composition and Water “Imbalance” in the Northern Himalayas. Water Resour. Res. 2023, 59, e2022WR034243. [Google Scholar] [CrossRef]
- Konapala, G.; Mishra, A.K.; Wada, Y.; Mann, M.E. Climate Change Will Affect Global Water Availability through Compounding Changes in Seasonal Precipitation and Evaporation. Nat. Commun. 2020, 11, 3044. [Google Scholar] [CrossRef]
- Masood, M.U.; Haider, S.; Rashid, M.; Aldlemy, M.S.; Pande, C.B.; Đurin, B.; Homod, R.Z.; Alshehri, F.; Elkhrachy, I. Quantifying the Impacts of Climate and Land Cover Changes on the Hydrological Regime of a Complex Dam Catchment Area. Sustainability 2023, 15, 15223. [Google Scholar] [CrossRef]
- Chakraborty, D.; Saha, S.; Sethy, B.K.; Singh, H.D.; Singh, N.; Sharma, R.; Chanu, A.N.; Walling, I.; Anal, P.R.; Chowdhury, S.; et al. Usability of the Weather Forecast for Tackling Climatic Variability and Its Effect on Maize Crop Yield in Northeastern Hill Region of India. Agronomy 2022, 12, 2529. [Google Scholar] [CrossRef]
- Saha, S.; Chakraborty, D.; Choudhury, B.U.; Singh, S.B.; Chinza, N.; Lalzarliana, C.; Dutta, S.K.; Chowdhury, S.; Boopathi, T. Lungmuana Spatial Variability in Temporal Trends of Precipitation and Its Impact on the Agricultural Scenario of Mizoram. Curr. Sci. 2015, 109, 2278–2282. [Google Scholar] [CrossRef]
- Chakraborty, D.; Saha, S.; Singh, R.K.; Sethy, B.K.; Kumar, A.; Saikia, U.S.; Das, S.K.; Makdoh, B.; Borah, T.R.; Nomita Chanu, A.; et al. Spatio-Temporal Trends and Change Point Detection in Rainfall in Different Parts of North-Eastern Indian States. J. Agrometeorol. 2017, 19, 160–163. [Google Scholar] [CrossRef]
- Kumar, K.R.; Kumar, K.K.; Ashrit, R.G.; Patwardhan, S.K.; Pant, G.B. Climate Change in India: Observations and Model Projections. In Climate Change and India-Issues, Concerns and Opportunity; Shukla, P.R., Sharma, S.K., Ramana, P.V., Eds.; Tata McGraw-Hill: New Delhi, India, 2002. [Google Scholar]
- India, G.G.E. Indian Network for Climate Change Assessment; Ministry of Environment and Forests: New Delhi, India, 2010. [Google Scholar]
- Naresh Kumar, S.; Singh, A.K.; Aggarwal, P.K.; Rao, V.U.M.; Venkateswarlu, B. Climate Change and Indian Agriculture Salient Achievements from ICAR Network Project; Indian Agricultural Research Institute Publications: New Delhi, India, 2012. [Google Scholar]
- Singh, R.B. Climate Change and Food Security. In Improving Crop Productivity in Sustainable Agriculture; Wiley: Hoboken, NJ, USA, 2012; pp. 1–22. [Google Scholar] [CrossRef]
- Singh, G. Climate Change and Food Security in India: Challenges and Opportunities. Irrig. Drain. 2016, 65, 5–10. [Google Scholar] [CrossRef]
- Guhathakurta, P.; Sreejith, O.P.; Menon, P.A. Impact of Climate Change on Extreme Rainfall Events and Flood Risk in India. J. Earth Syst. Sci. 2011, 120, 359–373. [Google Scholar] [CrossRef]
- Saha, S.; Chakraborty, D.; Paul, R.K.; Samanta, S.; Singh, S.B. Disparity in Rainfall Trend and Patterns among Different Regions: Analysis of 158 Years’ Time Series of Rainfall Dataset across India. Theor. Appl. Climatol. 2018, 134, 381–395. [Google Scholar] [CrossRef]
- Giri, K.; Mishra, G.; Rawat, M.; Pandey, S.; Bhattacharyya, R.; Bora, N.; Rai, J.P.N. Traditional Farming Systems and Agro-biodiversity in Eastern Himalayan Region of India. In Microbiological Advancements for Higher Altitude Agro-Ecosystems & Sustainability; Goel, R., Soni, R., Suyal, D., Eds.; Rhizosphere Biology; Springer: Singapore, 2020. [Google Scholar] [CrossRef]
- Majumdar, R.K. State of Biocultural Diversity, Climate Change and Ethnic Meat and Fish Products of Northeast India: A Review. In Impact of Climate Change on Hydrological Cycle, Ecosystem, Fisheries and Food Security; CRC Press: Boca Raton, FL, USA, 2022; pp. 425–437. [Google Scholar]
- Patra, S.; Rai, S.; Chakraborty, D.; Sangma, R.H.C.; Majumder, S.; Kuotsu, K.; Chakraborty, M.; Baiswar, P.; Singh, B.K.; Roy, A. Impact of Weather Variables on Radish Insect Pests in the Eastern Himalayas and Organic Management Strategies. Sustainability 2024, 16, 2946. [Google Scholar] [CrossRef]
- Deka, R.L.; Mahanta, C.; Nath, K.K. Trends and Fluctuations of Temperature Regime of North East India. In Proceedings of the ISPRS Proceedings, Impact of Climate Change on Agriculture XXXVIII-8/W3, Cape Town, South Africa, 12–17 July 2009; pp. 376–380. Available online: https://www.isprs.org/proceedings/xxxviii/8-w3/B6/8-45.pdf (accessed on 15 December 2024).
- Jhajharia, D.; Singh, V.P. Trends in Temperature, Diurnal Temperature Range and Sunshine Duration in Northeast India. Int. J. Climatol. 2011, 31, 1353–1367. [Google Scholar] [CrossRef]
- Jhajharia, D.; Dinpashoh, Y.; Kahya, E.; Singh, V.P.; Fakheri-Fard, A. Trends in Reference Evapotranspiration in the Humid Region of Northeast India. Hydrol. Process. 2012, 26, 421–435. [Google Scholar] [CrossRef]
- Jain, S.K.; Kumar, V.; Saharia, M. Analysis of Rainfall and Temperature Trends in Northeast India. Int. J. Climatol. 2013, 33, 968–978. [Google Scholar] [CrossRef]
- Chakraborty, D.; Singh, R.K.; Saha, S.; Roy, A.; Sethy, B.K.; Kumar, A.; Ngachan, S.V. Increase in Extreme Day Temperature in Hills of Meghalaya: Its Possible Ecological and Bio-Meteorological Effect. J. Agrometeorol. 2014, 16, 147–152. [Google Scholar]
- Sharma, D.; Das, S.; Goswami, B.N. Variability and Predictability of the Northeast India Summer Monsoon Rainfall. Int. J. Climatol. 2023, 43, 5248–5268. [Google Scholar] [CrossRef]
- Das, A.; Ghosh, P.K.; Choudhury, B.U.; Patel, D.P.; Munda, G.C.; Ngachan, S.V.; Chowdhury, P. Climate Change in North East India: Recent Facts and Events–Worry for Agricultural Management. In Proceedings of the ISPRS Proceedings, Impact of Climate Change on Agriculture XXXVIII-8/W3, Cape Town, South Africa, 12–17 July 2009; pp. 32–37. Available online: https://www.isprs.org/proceedings/xxxviii/8-w3/B1/2-114.pdf (accessed on 15 December 2024).
- Dash, S.K.; Kulkarni, M.A.; Mohanty, U.C.; Prasad, K. Changes in the Characteristics of Rain Events in India. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Kumar, S.; Sengupta, K.; Gogoi, B.J. Does Multifaceted Livelihood Intervention Improve Well-being: Reflections on a Case Study from North-eastern India. J. Int. Dev. 2023, 35, 2446–2464. [Google Scholar] [CrossRef]
- Birthal, P.S.; Khan, T.; Negi, D.S.; Agarwal, S. Impact of Climate Change on Yields of Major Food Crops in India: Implications for Food Security. Agric. Econ. Res. Rev. 2014, 27, 145–155. [Google Scholar] [CrossRef]
- Marak, J.D.K.; Sarma, A.K.; Bhattacharjya, R.K. Innovative Trend Analysis of Spatial and Temporal Rainfall Variations in Umiam and Umtru Watersheds in Meghalaya, India. Theor. Appl. Climatol. 2020, 142, 1397–1412. [Google Scholar] [CrossRef]
- Kuttippurath, J.; Murasingh, S.; Stott, P.A.; Sarojini, B.B.; Jha, M.K.; Kumar, P.; Nair, P.J.; Varikoden, H.; Raj, S.; Francis, P.A. Observed Rainfall Changes in the Past Century (1901–2019) over the Wettest Place on Earth. Environ. Res. Lett. 2021, 16, 024018. [Google Scholar] [CrossRef]
- Prokop, P.; Walanus, A. Variation in the Orographic Extreme Rain Events over the Meghalaya Hills in Northeast India in the Two Halves of the Twentieth Century. Theor. Appl. Climatol. 2015, 121, 389–399. [Google Scholar] [CrossRef]
- Goswami, B.B.; Mukhopadhyay, P.; Mahanta, R.; Goswami, B.N. Multiscale Interaction with Topography and Extreme Rainfall Events in the Northeast Indian Region. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Varikoden, H.; Revadekar, J. V On the Extreme Rainfall Events during the Southwest Monsoon Season in Northeast Regions of the Indian Subcontinent. Meteorol. Appl. 2020, 27, e1822. [Google Scholar] [CrossRef]
- Deka, R.L.; Mahanta, C.; Pathak, H.; Nath, K.K.; Das, S. Trends and Fluctuations of Rainfall Regime in the Brahmaputra and Barak Basins of Assam, India. Theor. Appl. Climatol. 2013, 114, 61–71. [Google Scholar] [CrossRef]
- Paul, A.R.; Maity, R. Future Projection of Climate Extremes across Contiguous Northeast India and Bangladesh. Sci. Rep. 2023, 13, 15616. [Google Scholar] [CrossRef] [PubMed]
- Jain, S.K.; Xu, C.-Y.; Zhou, Y. Change Analysis of All India and Regional Rainfall Data Series at Annual and Monsoon Scales. Hydrol. Res. 2023, 54, 606–632. [Google Scholar] [CrossRef]
- Govin, G.; Najman, Y.; Copley, A.; Millar, I.; Van der Beek, P.; Huyghe, P.; Grujic, D.; Davenport, J. Timing and Mechanism of the Rise of the Shillong Plateau in the Himalayan Foreland. Geology 2018, 46, 279–282. [Google Scholar] [CrossRef]
- Sarania, B.; Guttal, V.; Tamma, K. The Absence of Alternative Stable States in Vegetation Cover of Northeastern India. R. Soc. Open Sci. 2022, 9, 211778. [Google Scholar] [CrossRef]
- Saikia, P.; Kumar, A.; Khan, M.L. Biodiversity Status and Climate Change Scenario in Northeast India. In Climate Change Challenge (3C) and Social-Economic-Ecological Interface-Building: Exploring Potential Adaptation Strategies for Bio-Resource Conservation and Livelihood Development; Springer: Berlin/Heidelberg, Germany, 2016; pp. 107–120. [Google Scholar]
- Rao, V.B.; Franchito, S.H.; Gerólamo, R.O.P.; Giarolla, E.; Ramakrishna, S.S.V.S.; Rao, B.R.S.; Naidu, C.V. Himalayan Warming and Climate Change in India. Am. J. Clim. Chang. 2016, 5, 558–574. [Google Scholar] [CrossRef]
- Kothawale, D.R.; Rajeevan, M. Monthly, Seasonal and Annual Rainfall Time Series for All-India, Homogeneous Regions and Meteorological Sub-Divisions: 1871–2016; Indian Institute of Tropical Meteorology (IITM): Pune, India, 2017. [Google Scholar]
- Partal, T.; Kahya, E. Trend Analysis in Turkish Precipitation Data. Hydrol. Process. Int. J. 2006, 20, 2011–2026. [Google Scholar] [CrossRef]
- Malekian, A.; Kazemzadeh, M. Spatio-Temporal Analysis of Regional Trends and Shift Changes of Autocorrelated Temperature Series in Urmia Lake Basin. Water Resour. Manag. 2016, 30, 785–803. [Google Scholar] [CrossRef]
- Pal, I.; Al-Tabbaa, A. Assessing Seasonal Precipitation Trends in India Using Parametric and Non-Parametric Statistical Techniques. Theor. Appl. Climatol. 2011, 103, 1–11. [Google Scholar] [CrossRef]
- Şen, Z. Innovative Trend Analysis Methodology. J. Hydrol. Eng. 2012, 17, 1042–1046. [Google Scholar] [CrossRef]
- Şen, Z.; Şen, Z. Innovative Trend Analyses. In Innovative Trend Methodologies in Science and Engineering; Springer: Berlin/Heidelberg, Germany, 2017; pp. 175–226. [Google Scholar]
- Singh, R.N.; Sah, S.; Das, B.; Potekar, S.; Chaudhary, A.; Pathak, H. Innovative Trend Analysis of Spatio-Temporal Variations of Rainfall in India during 1901–2019. Theor. Appl. Climatol. 2021, 145, 821–838. [Google Scholar] [CrossRef]
- Pettitt, A.N. A Non-parametric Approach to the Change-point Problem. J. R. Stat. Soc. Ser. C Appl. Stat. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Zarenistanak, M.; Dhorde, A.G.; Kripalani, R.H. Trend Analysis and Change Point Detection of Annual and Seasonal Precipitation and Temperature Series over Southwest Iran. J. Earth Syst. Sci. 2014, 123, 281–295. [Google Scholar] [CrossRef]
- Alexandersson, H. A Homogeneity Test Applied to Precipitation Data. J. Climatol. 1986, 6, 661–675. [Google Scholar] [CrossRef]
- Buishand, T.A. Some Methods for Testing the Homogeneity of Rainfall Records. J. Hydrol. 1982, 58, 11–27. [Google Scholar] [CrossRef]
- Klein Tank, A. EUMETNET/ECSN Optional Programme: European Climate Assessment & Dataset (ECA&D) Algorithm Theoretical Basis Document (ATBD); Version 4, Report EPJ029135 2007; Royal Netherlands Meteorological Institute KNMI: Utrecht, The Netherlands, 2007. [Google Scholar]
- Ibrahim, B.; Karambiri, H.; Polcher, J.; Yacouba, H.; Ribstein, P. Changes in Rainfall Regime over Burkina Faso under the Climate Change Conditions Simulated by 5 Regional Climate Models. Clim. Dyn. 2014, 42, 1363–1381. [Google Scholar] [CrossRef]
- Harley, C.D.G. Climate Change, Keystone Predation, and Biodiversity Loss. Science 2011, 334, 1124–1127. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, D.; Sehgal, V.K.; Dhakar, R.; Varghese, E.; Das, D.K.; Ray, M. Changes in Daily Maximum Temperature Extremes across India over 1951–2014 and Their Relation with Cereal Crop Productivity. Stoch. Environ. Res. Risk Assess. 2018, 32, 3067–3081. [Google Scholar] [CrossRef]
- Te Chow, V. Handbook of Applied Hydrology: A Compendium of Water-Resources Technology; McGraw-Hill Company: New York, NY, USA, 1964. [Google Scholar]
- Chakraborty, D.; Sehgal, V.K.; Dhakar, R.; Ray, M.; Das, D.K. Spatio-Temporal Trend in Heat Waves over India and Its Impact Assessment on Wheat Crop. Theor. Appl. Climatol. 2019, 138, 1925–1937. [Google Scholar] [CrossRef]
- Hare, W. Assessment of Knowledge on Impacts of Climate Change–Contribution. Arctic 2003, 100, 25–35. [Google Scholar]
- Mazdiyasni, O.; AghaKouchak, A.; Davis, S.J.; Madadgar, S.; Mehran, A.; Ragno, E.; Sadegh, M.; Sengupta, A.; Ghosh, S.; Dhanya, C.T. Increasing Probability of Mortality during Indian Heat Waves. Sci. Adv. 2017, 3, e1700066. [Google Scholar] [CrossRef]
- Sattar, A.; Khan, S.A.; Banerjee, S. Assured Rainfall Analysis for Enhanced Crop Production under Rainfed Condition in Bihar. J. Agrometeorol. 2018, 20, 332–335. [Google Scholar] [CrossRef]
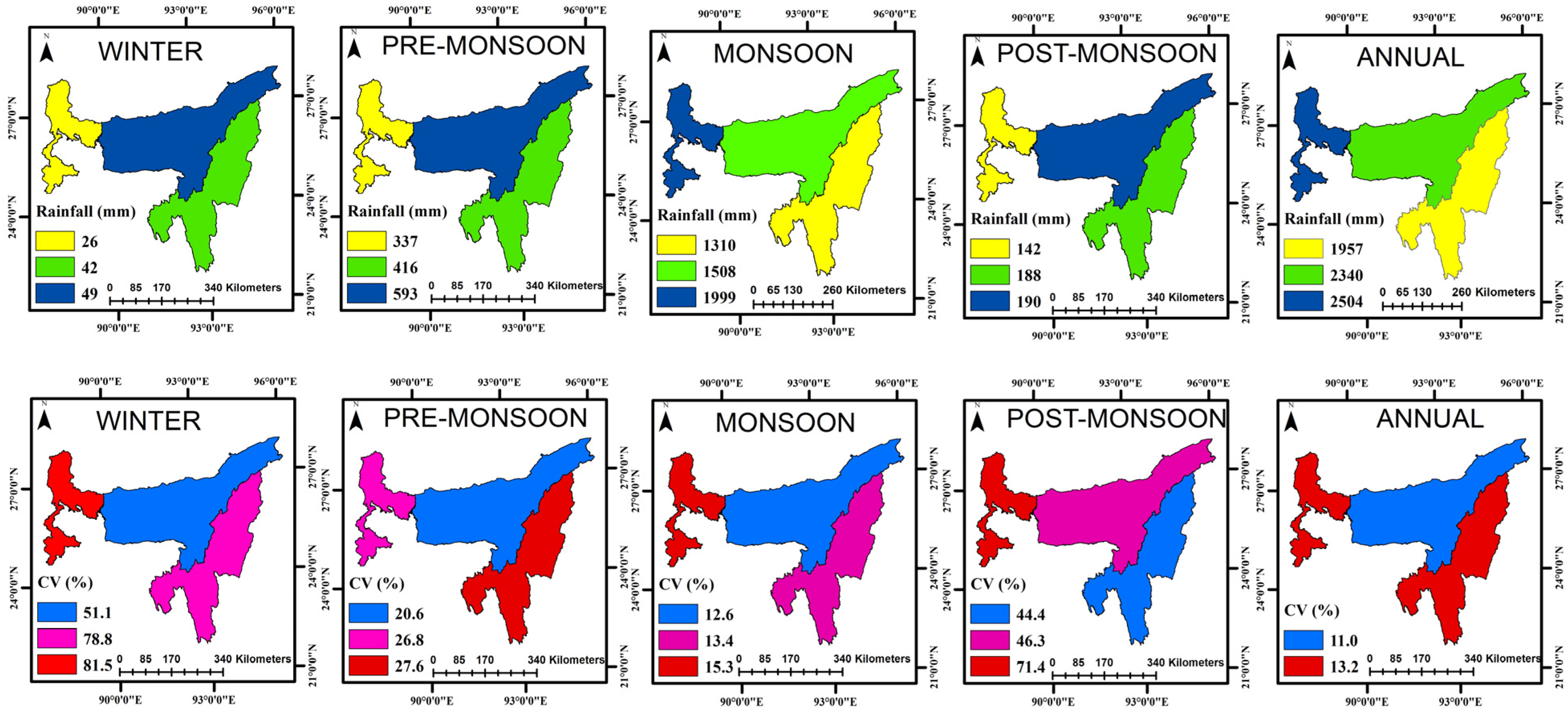


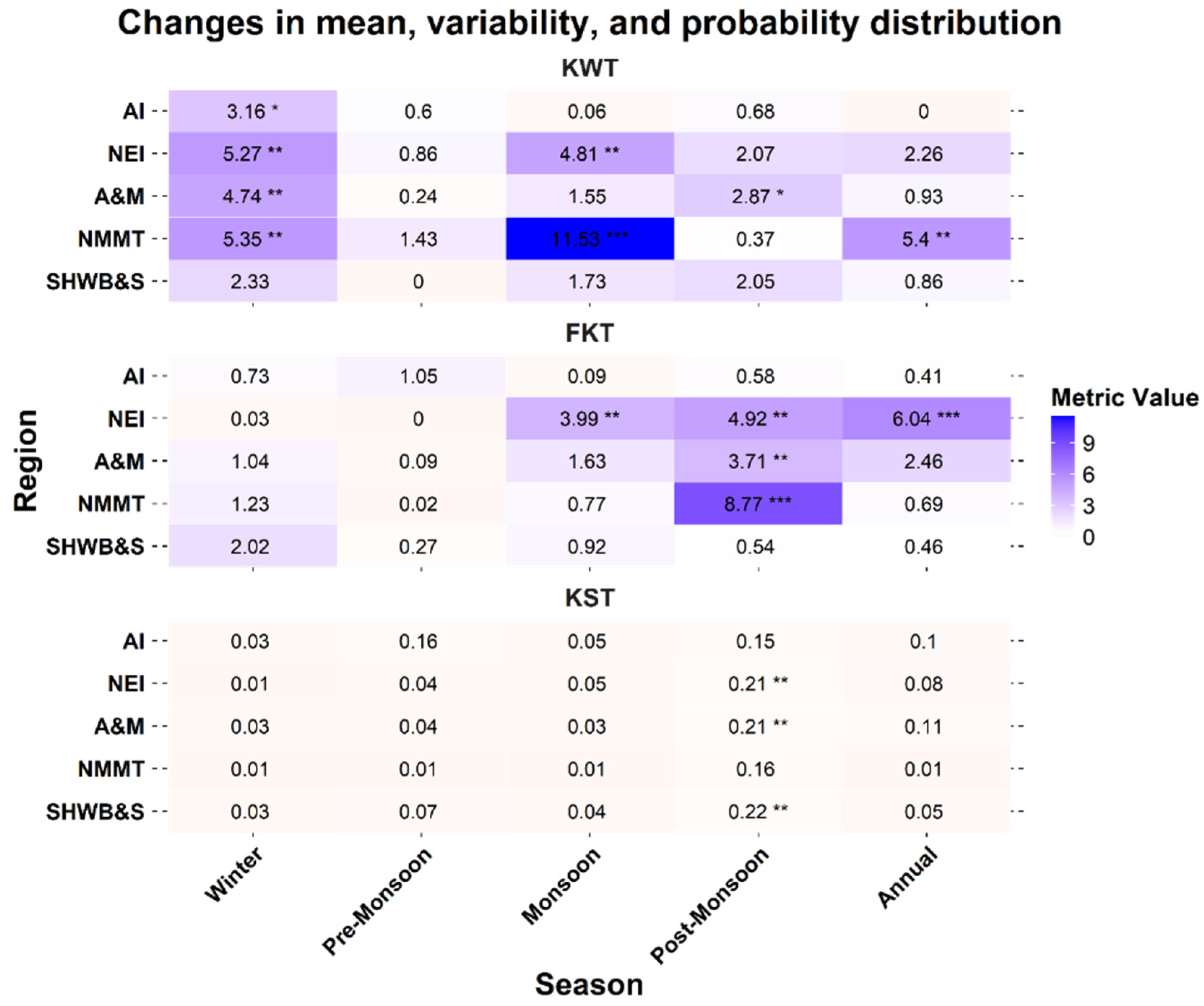

| Min | Max | CS | CK | ||
|---|---|---|---|---|---|
| All India (AI) | Winter | 3.0 | 61.1 | 0.7 | 3.2 |
| Pre-Monsoon | 55.2 | 166.5 | 0.7 | 3.7 | |
| Monsoon | 604.0 | 1020.2 | −0.5 | 2.9 | |
| Post-Monsoon | 50.1 | 209.9 | 0.4 | 2.7 | |
| Annual | 810.9 | 1347.0 | 0.0 | 3.1 | |
| Northeastern India (NEI) | Winter | 0.9 | 118.2 | 0.7 | 3.5 |
| Pre-Monsoon | 226.6 | 656.5 | 0.2 | 2.7 | |
| Monsoon | 1139.9 | 1792.9 | 0.2 | 2.9 | |
| Post-Monsoon | 26.3 | 373.8 | 0.4 | 2.8 | |
| Annual | 1576.4 | 2504.4 | 0.0 | 2.8 | |
| Assam and Meghalaya (A&M) | Winter | 1.3 | 149.2 | 0.7 | 4.0 |
| Pre-Monsoon | 330.5 | 1030.5 | 0.6 | 3.4 | |
| Monsoon | 1068.8 | 2079.5 | 0.2 | 3.0 | |
| Post-Monsoon | 51.8 | 484.9 | 0.9 | 3.8 | |
| Annual | 1779.9 | 3102.9 | 0.2 | 3.1 | |
| Nagaland, Manipur, Mizoram, and Tripura (NMMT) | Winter | 0.4 | 201.2 | 1.6 | 6.7 |
| Pre-Monsoon | 142.3 | 685.3 | 0.1 | 2.4 | |
| Monsoon | 928.0 | 1812.8 | 0.5 | 3.3 | |
| Post-Monsoon | 8.9 | 429.9 | 0.4 | 2.8 | |
| Annual | 1406.4 | 2742.3 | 0.2 | 3.0 | |
| Sub-Himalayan West Bengal and Sikkim (SHWB&S) | Winter | 0.2 | 112.3 | 1.5 | 6.2 |
| Pre-Monsoon | 98.1 | 650.8 | 0.8 | 4.5 | |
| Monsoon | 1204.5 | 2805.7 | 0.3 | 2.9 | |
| Post-Monsoon | 7.1 | 565.6 | 1.2 | 4.6 | |
| Annual | 1705.9 | 3393.6 | 0.1 | 2.9 |
| Full Series (1871–2016) | P-I (1871–1943) | P-II (1944–2016) | |||||
|---|---|---|---|---|---|---|---|
| OLS-Slope | Sen-Slope | OLS-Slope | Sen-Slope | OLS-Slope | Sen-Slope | ||
| All India | Winter | −0.02 | −0.01 | 0.18 *** | 0.21 *** | −0.04 | −0.02 |
| Pre-Monsoon | 0.03 | 0.03 | 0.02 | 0.02 | 0.04 | 0.01 | |
| Monsoon | −0.18 | −0.21 | −0.22 | −0.41 | −0.94 ** | −0.93 ** | |
| Post-Monsoon | 0.04 | 0.04 | 0.15 | 0.13 | −0.22 | −0.18 | |
| Annual | −0.13 | −0.1 | 0.13 | 0.12 | −1.15 ** | −1.15 * | |
| Northeastern India | Winter | −0.08 * | −0.08 * | 0.07 | 0.1 | −0.08 | −0.06 |
| Pre-Monsoon | −0.14 | −0.14 | −0.1 | −0.06 | −0.27 | −0.07 | |
| Monsoon | −0.66 *** | −0.81 *** | 0.01 | −0.06 | −1.8 ** | −2.03 *** | |
| Post-Monsoon | 0.15 | 0.17 | 0.33 | 0.44 | −0.85 ** | −0.77 * | |
| Annual | −0.74 ** | −0.9 ** | 0.31 | 0.06 | −3 *** | −3.17 *** | |
| Assam and Meghalaya | Winter | −0.08 * | −0.09 * | 0.05 | 0.06 | −0.1 | −0.09 |
| Pre-Monsoon | −0.23 | −0.26 | 0.05 | −0.19 | −1.19 * | −1.32 * | |
| Monsoon | −0.74 ** | −0.73 ** | 0.05 | −0.25 | −2.66 ** | −2.84 ** | |
| Post-Monsoon | 0.21 | 0.17 | 0.44 | 0.55 | −1.16 ** | −1.11 ** | |
| Annual | −0.85 * | −0.97 * | 0.59 | 0.24 | −5.11 *** | −4.98 *** | |
| Nagaland, Manipur, Mizoram, and Tripura | Winter | −0.13 ** | −0.11 ** | 0.02 | 0.03 | −0.13 | −0.11 |
| Pre-Monsoon | −0.23 | −0.26 | −0.19 | −0.2 | 0 | −0.06 | |
| Monsoon | −1.64 *** | −1.54 *** | −1.57 * | −1.06 | −3.93 *** | −3.6 *** | |
| Post-Monsoon | 0.08 | 0.03 | 0.2 | 0.26 | −0.87 * | −0.9 | |
| Annual | −1.92 *** | −1.89 *** | −1.54 | −1.51 | −4.94 *** | −5.3 *** | |
| Sub-Himalayan West Bengal and Sikkim | Winter | −0.04 | −0.03 | 0.07 | 0.07 | −0.03 | 0.01 |
| Pre-Monsoon | 0.06 | 0.12 | 0.52 | 0.53 | 0.08 | 0.37 | |
| Monsoon | −0.37 | −0.62 | 0.94 | 0.45 | 0.48 | 0.3 | |
| Post-Monsoon | 0.21 | 0.23 | 0.72 | 0.53 | −0.3 | −0.2 | |
| Annual | −0.14 | −0.37 | 2.26 | 1.47 | 0.23 | −0.32 | |
| Pettit | SNHT | BHRT | ||
|---|---|---|---|---|
| All India | Winter | 1948 *** | 1948 | 1949 *** |
| Pre-Monsoon | 1935 ** | 2014 | 1936 | |
| Monsoon | 1964 * | 1964 | 1965 | |
| Post-Monsoon | 1914 *** | 1876 | 1915 | |
| Annual | 1964 *** | 1964 | 1965 | |
| Northeastern India | Winter | 1945 *** | 2008 | 1946 |
| Pre-Monsoon | 1956 *** | 1956 | 1957 | |
| Monsoon | 1956 *** | 2000 *** | 1957 ** | |
| Post-Monsoon | 1908 *** | 2005 | 1945 | |
| Annual | 1956 *** | 2007 *** | 1957 ** | |
| Assam and Meghalaya | Winter | 1945 *** | 2008 *** | 1946 |
| Pre-Monsoon | 1959 *** | 1959 | 1960 | |
| Monsoon | 1956 *** | 2000 *** | 1957 | |
| Post-Monsoon | 1908 *** | 1908 | 1945 | |
| Annual | 1956 *** | 2005 *** | 1957 | |
| Nagaland, Manipur, Mizoram, and Tripura | Winter | 1945 *** | 1945 | 1946 |
| Pre-Monsoon | 1895 ** | 1895 | 1896 | |
| Monsoon | 1969 ** | 1969 *** | 1969 *** | |
| Post-Monsoon | 1891 | 2010 | 1946 | |
| Annual | 1956 *** | 2004 *** | 1957 *** | |
| Sub-Himalayan West Bengal and Sikkim | Winter | 1945 *** | 1962 | 1963 |
| Pre-Monsoon | 1997 | 1876 | 1957 | |
| Monsoon | 1939 *** | 2000 | 1940 | |
| Post-Monsoon | 1908 *** | 1908 | 1909 | |
| Annual | 1956 | 1873 | 1957 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chakraborty, D.; Roy, A.; Singh, N.U.; Saha, S.; Das, S.K.; Mridha, N.; Yumnam, A.; Paul, P.; Gowda, C.; Biam, K.P.; et al. Assessing Climate Change Impact on Rainfall Patterns in Northeastern India and Its Consequences on Water Resources and Rainfed Agriculture. Earth 2025, 6, 2. https://doi.org/10.3390/earth6010002
Chakraborty D, Roy A, Singh NU, Saha S, Das SK, Mridha N, Yumnam A, Paul P, Gowda C, Biam KP, et al. Assessing Climate Change Impact on Rainfall Patterns in Northeastern India and Its Consequences on Water Resources and Rainfed Agriculture. Earth. 2025; 6(1):2. https://doi.org/10.3390/earth6010002
Chicago/Turabian StyleChakraborty, Debasish, Aniruddha Roy, Nongmaithem Uttam Singh, Saurav Saha, Shaon Kumar Das, Nilimesh Mridha, Anjoo Yumnam, Pampi Paul, Chikkathimme Gowda, Kamni Paia Biam, and et al. 2025. "Assessing Climate Change Impact on Rainfall Patterns in Northeastern India and Its Consequences on Water Resources and Rainfed Agriculture" Earth 6, no. 1: 2. https://doi.org/10.3390/earth6010002
APA StyleChakraborty, D., Roy, A., Singh, N. U., Saha, S., Das, S. K., Mridha, N., Yumnam, A., Paul, P., Gowda, C., Biam, K. P., Patra, S., Amrutha, T., Singh, B. P., & Mishra, V. K. (2025). Assessing Climate Change Impact on Rainfall Patterns in Northeastern India and Its Consequences on Water Resources and Rainfed Agriculture. Earth, 6(1), 2. https://doi.org/10.3390/earth6010002







