Selection of Appropriate Coastal Protection Structure Using AHP Method †
Abstract
:1. Introduction
2. Materials and Methods
2.1. AHP Method
- Defining the problem (the goal, the criteria, the alternatives) and defining the hierarchy;
- Performing a pair-wise comparison of criteria in respect to the goal or defining the weight/importance of each criterion (this must be done also for sub-criteria with respect to criteria);
- Performing a pair-wise comparison of the alternatives with respect to each criterion or evaluating the alternatives against each criterion;
- Applying the AHP method to estimate the overall priority vector of the alternatives with respect to the goal;
- Forming the rank-list of alternatives;
- Performing the sensitivity analysis;
- Making the final decision.
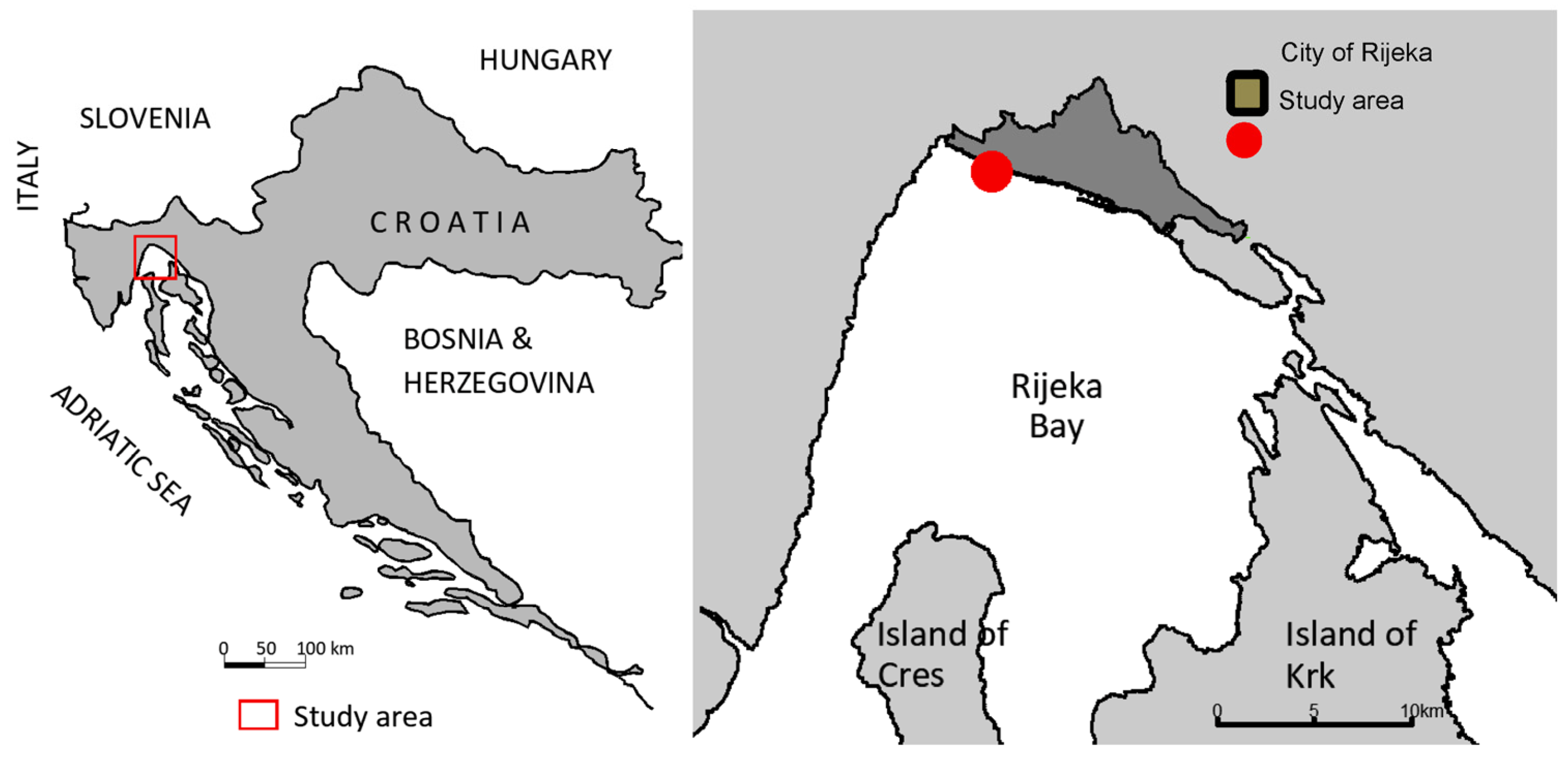
2.2. Case Study
3. Results
3.1. Definition of Criteria
- the decrease in the significant wave height along the new and existing coastal structure (T1)—this is directly related to the wave forces acting on the structure (stronger reduction of the wave heights suggests lower wave forces and less potential damages to the structure);
- the dissipation of the wave energy (T2)—the wave energy should be dissipated as much as possible and as far as possible from the structure to ensure that no breaking waves reach the beach structure; and
- the effect on the protection of the newly built coastal structure (T3)—coastal structures, such as the concrete walls, can be vulnerable to the scouring at the toe, which may have a negative impact on the structure stability, therefore a rubble protection placed in front of the concrete wall has an additional positive effect.
- the complexity of the structure of the breakwater (EC1)—if the breakwater is placed close to (in front of) the coastal wall, it can be built directly from the beach, which is more practical and less expensive than building a detached breakwater from a floating equipment; and
- the volume of the breakwater (how much material is needed) (EC2)—the volume of the breakwater is directly related to the volume of rubble mound material and the price of the construction.
3.2. Pairwise Comparison of Alternatives
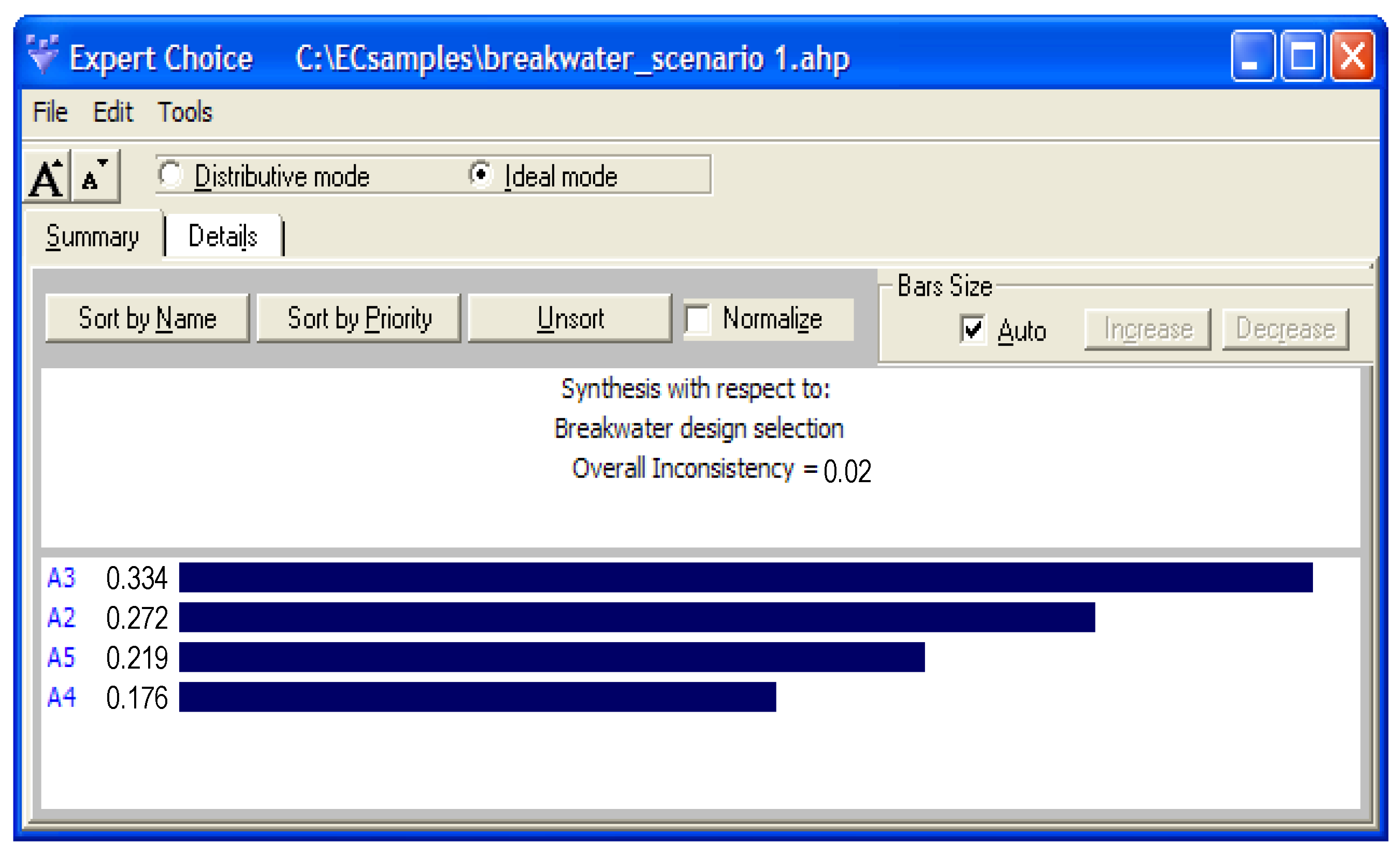
3.3. Results from AHP
- Scenario S2: T 25%, EC 35%, EN 30% and S 10%—more importance is given to the environmental criterion; technical, economic and social criteria are given less importance in comparison to S1;
- Scenario S3: T 45%, EC 35%, EN 10% and S 10%—more importance is given to the technical criterion; economic, environmental and social criteria are given less importance in comparison to S1;
- Scenario S4: T 40%, EC 30%, EN 15% and S 15%—more importance is given to the technical criterion, less to economic one, with no change in the environmental and social criteria importance in comparison to S1; and
- Scenario S5: T 30%, EC 50%, EN 10% and S 10%—more importance is given to the economic criterion, less to the technical, environmental and social criteria in comparison to S1.
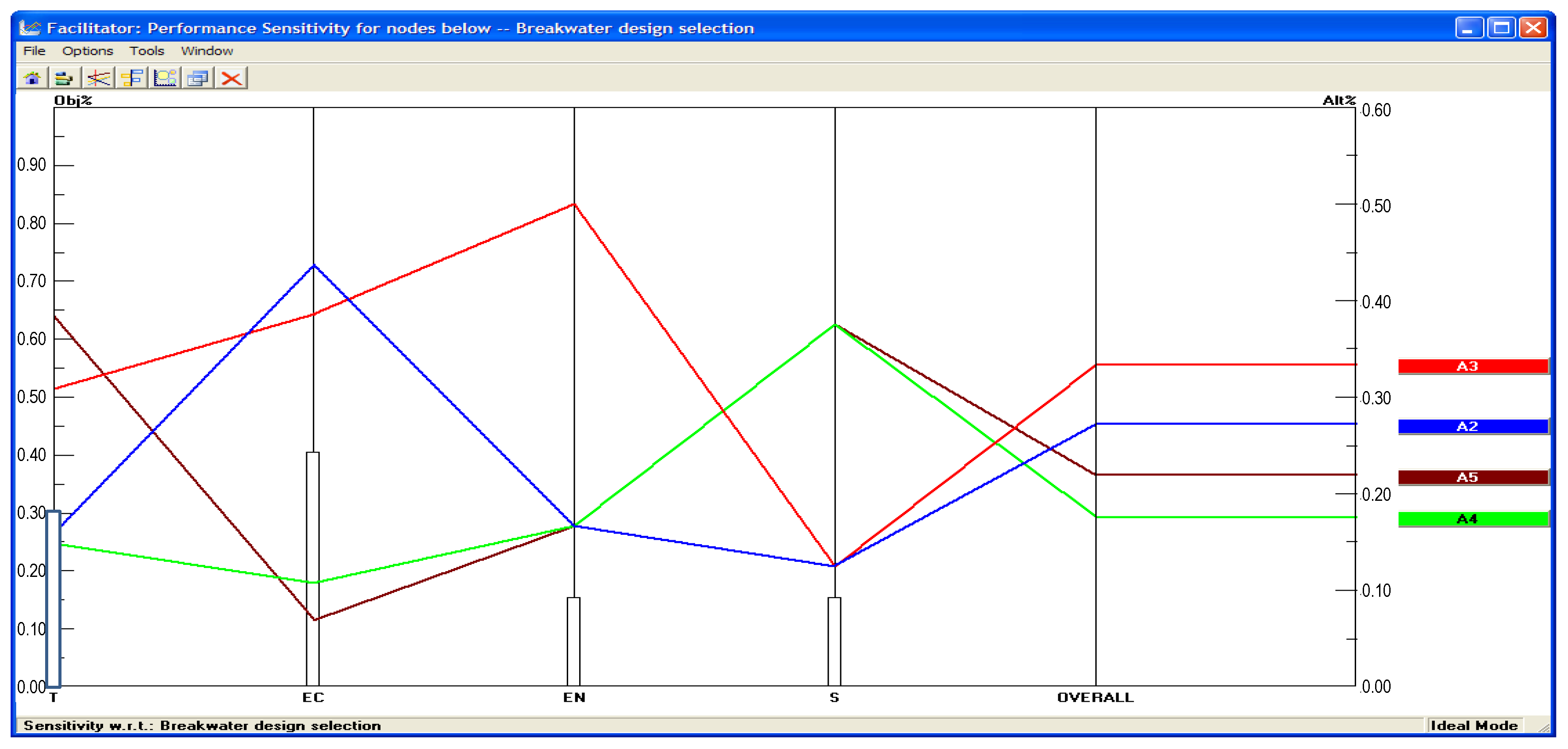
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Triantaphyllou, E. Multi-Criteria Decision Making Methods: A Comparative Study; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2000; ISBN 978-0-7923-6607-2. [Google Scholar] [CrossRef]
- Figueira, J.; Greco, S.; Ehrogott, M. Multiple Criteria Decision Analysis: State of the Art Surveys. In International Series in Operations Research & Management Science; Springer: New York, NY, USA, 2005; Volume 78, ISBN 978-0-387-23081-8. [Google Scholar] [CrossRef]
- Huang, I.B.; Keisler, J.; Linkov, I. Multi-criteria decision analysis in environmental sciences: Ten years of applications and trends. Sci. Total Environ. 2011, 409, 3578–3794. [Google Scholar] [CrossRef] [PubMed]
- Hajkowicz, S.; Collins, K. A Review of Multiple Criteria Analysis for Water Resource Planning and Management. Water Resour. Manag. 2007, 21, 1553–1566. [Google Scholar] [CrossRef]
- Serafim, M.B.; Siegle, E.; Corsi, A.C.; Bonetti, J. Coastal vulnerability to wave impacts using a multi-criteria index: Santa Catarina (Brazil). J. Environ. Manag. 2019, 230, 21–32. [Google Scholar] [CrossRef] [PubMed]
- Papatheochari, T.; Coccossis, H. Development of a waterfront regeneration tool to support local decision making in the context of integrated coastal zone management. Ocean Coast. Manag. 2019, 169, 284–295. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Bagočius, V. Multi-criteria selection of a deep-water port in the Eastern Baltic Sea. Appl. Soft Comput. 2015, 26, 180–192. [Google Scholar] [CrossRef]
- Johnston, A.; Slovinsky, P.; Yates, K.L. Assessing the vulnerability of coastal infrastructure to sea level rise using multi-criteria analysis in Scarborough, Maine (USA). Ocean Coast. Manag. 2014, 95, 176–188. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process, 2nd ed.; RWS Publications: Pittsburg, CA, USA, 1996. [Google Scholar]
- Grahovac, A.; Krvavica, N.; Ružić, I. Seawall construction impact on wave dynamics of natural coast. Zbornik Radova Građevinskog Fakulteta u Rijeci 2018, 21, 179–191. (In Croatian) [Google Scholar] [CrossRef]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions, Part I: Model description and validation. J. Geophys. Res. 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- Pizzolon, M.; Cenci, E.; Mazzoldi, C. The onset of fish colonization in a coastal defence structure (Chioggia, Northern Adriatic Sea). Estuar. Coast. Shelf Sci. 2008, 78, 166–178. [Google Scholar] [CrossRef]
- Postacchini, M.; Lalli, F.; Memmola, F.; Bruschi, A.; Bellafiore, D.; Lisi, I.; Zitti, G.; Brocchini, M. Model chain approach for coastal inundation: Application to the bay of Alghero. Est. Coast. Shelf Sci. 2019, 219, 56–70. [Google Scholar] [CrossRef]
| Intensity of Weight, Importance, Preference | Definition |
|---|---|
| 1 | Equal importance (no preference) |
| 3 | Moderate importance (moderate preference) |
| 5 | Strong importance (strong preference) |
| 7 | Very strong importance (very strong preference) |
| 9 | Extreme importance (extreme preference) |
| 2, 4, 6, 8 | Intermediate values |
| Alternatives | Characteristics of the Breakwater | Complexity of the Construction | Decrease in Wave Height | Wave Energy Dissipation | Protection of Coastal Structure | Environmental Impacts | Social Impacts |
|---|---|---|---|---|---|---|---|
| A1 | no breakwater | no breakwater construction | none | none | none | n/a | n/a |
| A2 | made of large stone elements, connected to the shore (length 100 m, crest height −2.0 m and width 6.0 m, the crest altitude on the beach side is higher −1.5 m for beach protection, max. depth is—6.5 m, volume 2150 m3) | simpler and cheaper than the construction of the breakwater in alternative A4 and A5 because it is possible to construct it by filling the material from the shore—without offshore construction equipment | av. by 17%, max. by 23% | high, energy is dissipated very close to the structure | provides protection for natural beach material, protects the structure from scouring | provides a significant area near the coastline for new bio habitat | some negative impacts during extreme ebb phases, due to reduced water depth and unappealing sea bed where swimmers enter the water |
| A3 | made of large stone elements, connected to the shore (4.0 m wider than A2, length 110 m, crest height −2.0 m, the crest altitude on the beach side is higher −1.5 m for beach protection, max. depth is—7.5 m, volume 2870 m3) | simpler and cheaper than the construction of the breakwater in alternative A4 and A5 because it is possible to construct it by filling the material from the shore—without offshore construction equipment, more material is needed than in A2 | av. by 18%, max. by 28% | high, energy is dissipated close to the structure | provides protection for natural beach material, protects the structure from scouring, slightly better than A2 | provides a significant area near the coastline for new bio habitat, better than A2, A4, A5 | some negative impacts during extreme ebb phases, due to reduced water depth and unappealing sea bed where swimmers enter the water (similar to A2) |
| A4 | made of large stone elements, with a trapezoidal cross-section detached from shore (length 110 m, crest height −2.0 m and width 6.0 m, the axis is at an average depth of −5.0 m, volume 3200 m3) | complex and more expensive than A2 and A3 because of the distance of the breakwater from shore and need for offshore construction equipment | av. by 15%, max. by 28% | high, energy is dissipated far from the structure | provides protection for natural beach material, does not protect the structure from scouring, similar to A5, worse than A2 | provides a significant area far from the coastline for new bio habitat, similar to A2, A5 | insignificant impact during extreme ebb phases for potential boat approach |
| A5 | made of large stone elements, with trapezoidal cross-section detached from shore (length 125 m, crest height −2.0 m and width 6.0 m, the breakwater axis is at an average depth of −6.0 m, volume of material 4100 m3) | complex and more expensive than A2 and A3 because of the distance of the breakwater from shore and need for offshore construction equipment, more material is needed than in A4 | av. by 17%, max. by 33% | high, energy is dissipated very far from the structure | provides protection for natural beach material, does not protect the structure from scouring similar to A4 and worse than A2 | provides a significant area far from the coastline for new bio habitat, similar to A2 and A4 | insignificant impact during extreme ebb phases for potential boat approach |
| T1 | A2 | A3 | A4 | A5 | T2 | A2 | A3 | A4 | A5 | T3 | A2 | A3 | A4 | A5 |
| A2 | −4 | −3 | −6 | A2 | −3 | −5 | −7 | A2 | −2 | 7 | 7 | |||
| A3 | 3 | −3 | A3 | −3 | −5 | A3 | 8 | 8 | ||||||
| A4 | −4 | A4 | −3 | A4 | 1 | |||||||||
| A5 | A5 | A5 | ||||||||||||
| EC1 | A2 | A3 | A4 | A5 | EC2 | A2 | A3 | A4 | A5 | |||||
| A2 | 1 | 5 | 5 | A2 | 3 | 5 | 7 | |||||||
| A3 | 5 | 5 | A3 | 3 | 5 | |||||||||
| A4 | 1 | A4 | 3 | |||||||||||
| A5 | A5 | |||||||||||||
| EN | A2 | A3 | A4 | A5 | ||||||||||
| A2 | −3 | 1 | 1 | |||||||||||
| A3 | 3 | 3 | ||||||||||||
| A4 | 1 | |||||||||||||
| A5 | ||||||||||||||
| S | A2 | A3 | A4 | A5 | ||||||||||
| A2 | 1 | −3 | −3 | |||||||||||
| A3 | −3 | −3 | ||||||||||||
| A4 | 1 | |||||||||||||
| A5 |
| Rank | Scenario | ||||
|---|---|---|---|---|---|
| S1 | S2 | S3 | S4 | S5 | |
| 1 | A3 (0.334) | A3 (0.369) | A3 (0.333) | A3 (0.326) | A3 (0.345) |
| 2 | A2 (0.272) | A2 (0.262) | A2 (0.262) | A5 (0.249) | A2 (0.303) |
| 3 | A5 (0.219) | A5 (0.203) | A5 (0.241) | A2 (0.244) | A5 (0.196) |
| 4 | A4 (0.175) | A4 (0.167) | A4 (0.163) | A4 (0.181) | A4 (0.157) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karleuša, B.; Krvavica, N.; Ružić, I. Selection of Appropriate Coastal Protection Structure Using AHP Method. Environ. Sci. Proc. 2020, 2, 4. https://doi.org/10.3390/environsciproc2020002004
Karleuša B, Krvavica N, Ružić I. Selection of Appropriate Coastal Protection Structure Using AHP Method. Environmental Sciences Proceedings. 2020; 2(1):4. https://doi.org/10.3390/environsciproc2020002004
Chicago/Turabian StyleKarleuša, Barbara, Nino Krvavica, and Igor Ružić. 2020. "Selection of Appropriate Coastal Protection Structure Using AHP Method" Environmental Sciences Proceedings 2, no. 1: 4. https://doi.org/10.3390/environsciproc2020002004
APA StyleKarleuša, B., Krvavica, N., & Ružić, I. (2020). Selection of Appropriate Coastal Protection Structure Using AHP Method. Environmental Sciences Proceedings, 2(1), 4. https://doi.org/10.3390/environsciproc2020002004







