Forecasting Monthly Rainfall of Karyes, Chios Island, Greece, Central-Eastern Mediterranean Basin Using the ARIMA Method †
Abstract
:1. Introduction
2. Methodology
2.1. Study Area
2.2. The Box–Jenkins Model-Building Procedure
2.2.1. Model Identification and Selection
2.2.2. Model Parameters Estimation
2.2.3. Model Checking and Forecasting
2.3. Types of ARIMA Models
2.3.1. Autoregressive (AR) and Moving Average (MA) Models
2.3.2. Autoregressive Moving Average (ARMA) Models
2.3.3. Seasonal ARIMA (SARIMA) Models
3. Results
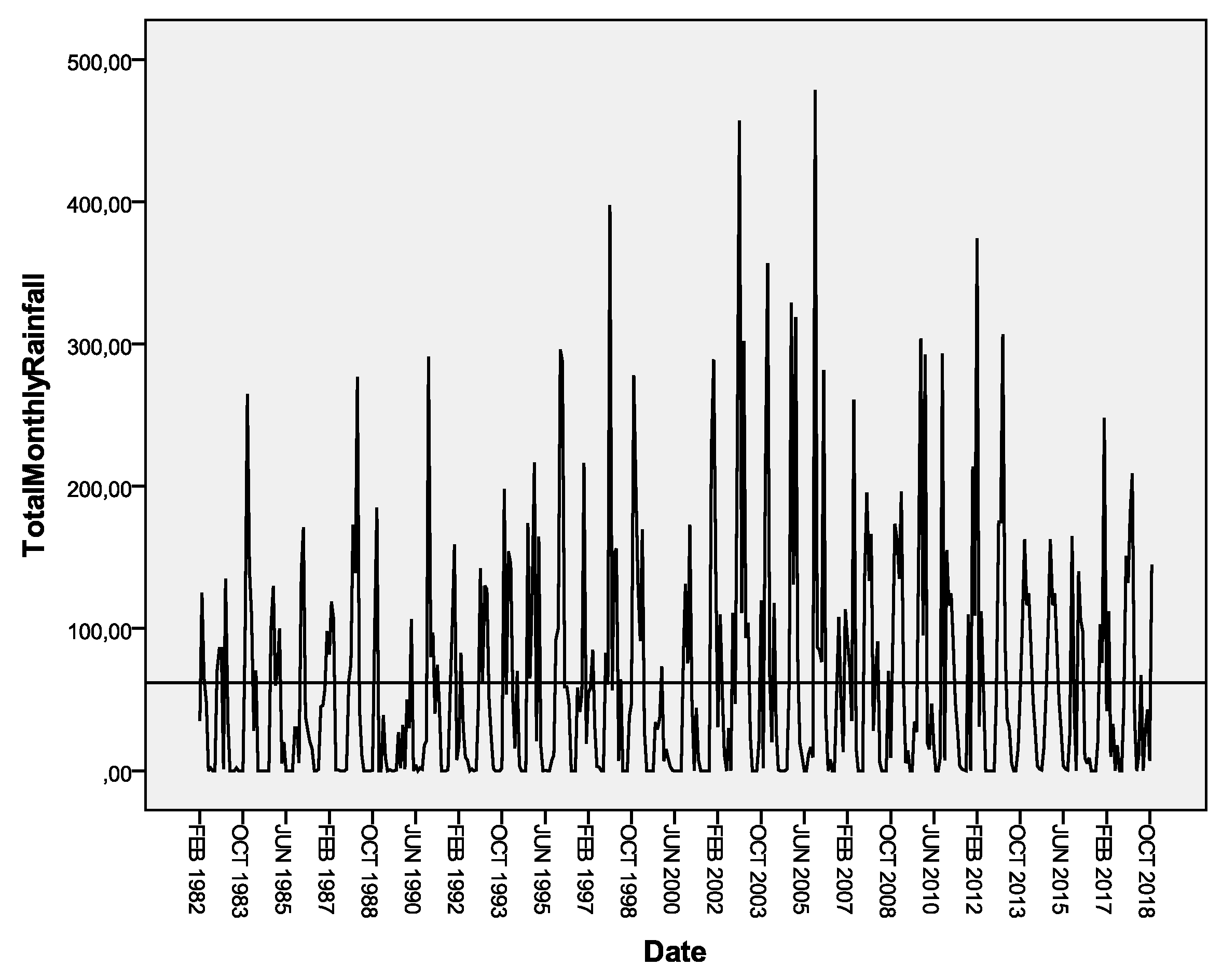
3.1. Primordial Data Analysis
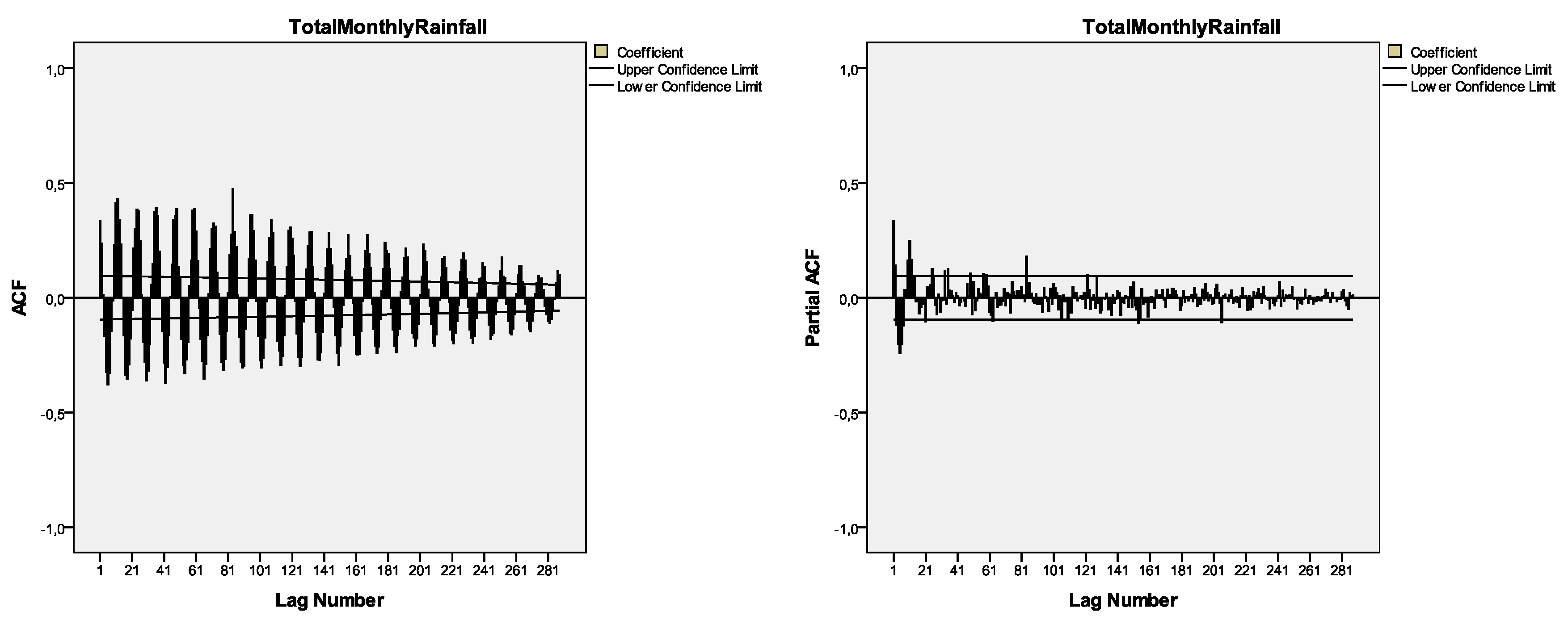
3.2. Data Stationarity Check
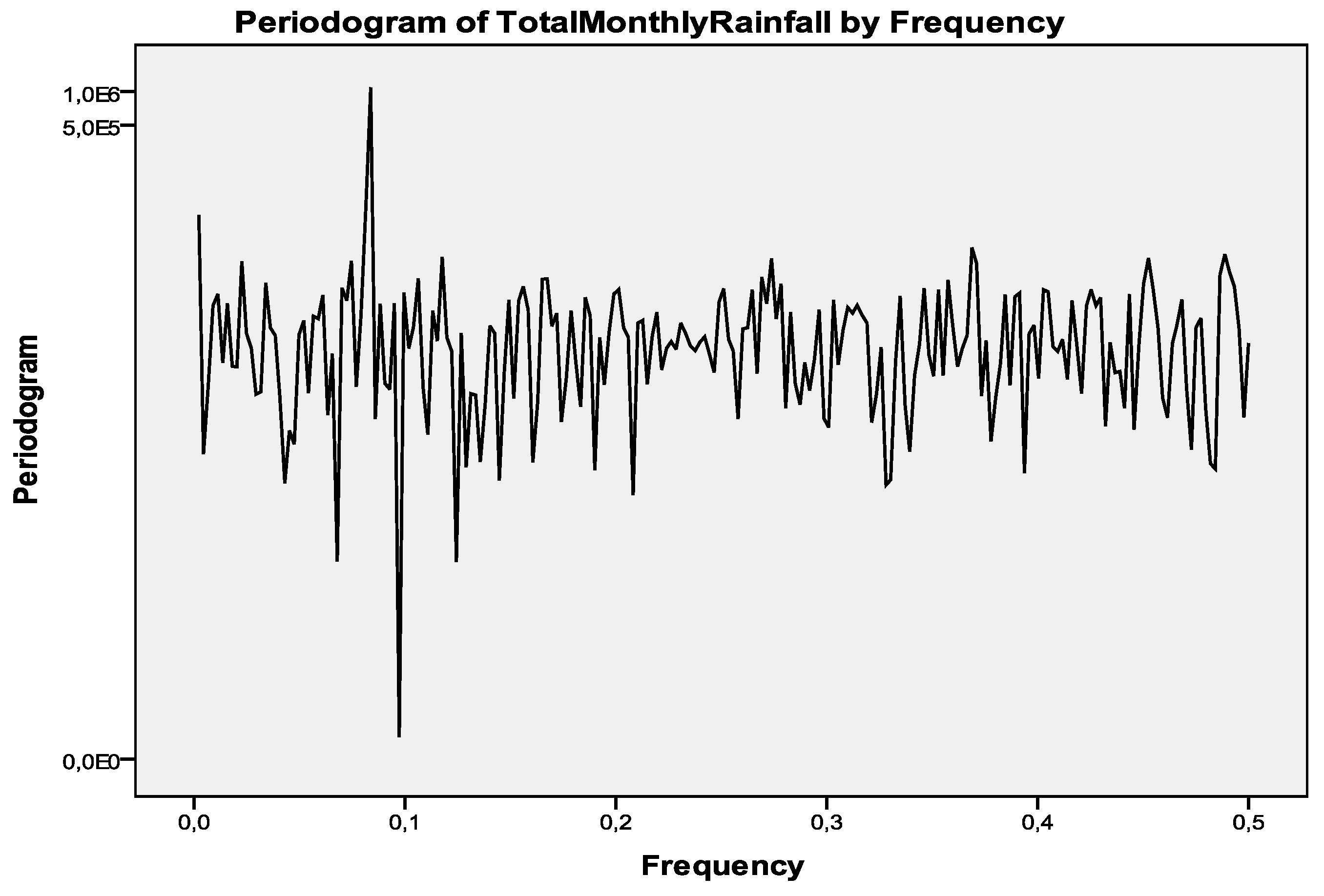
3.3. Data Differencing (Seasonality)
3.4. Model Identification
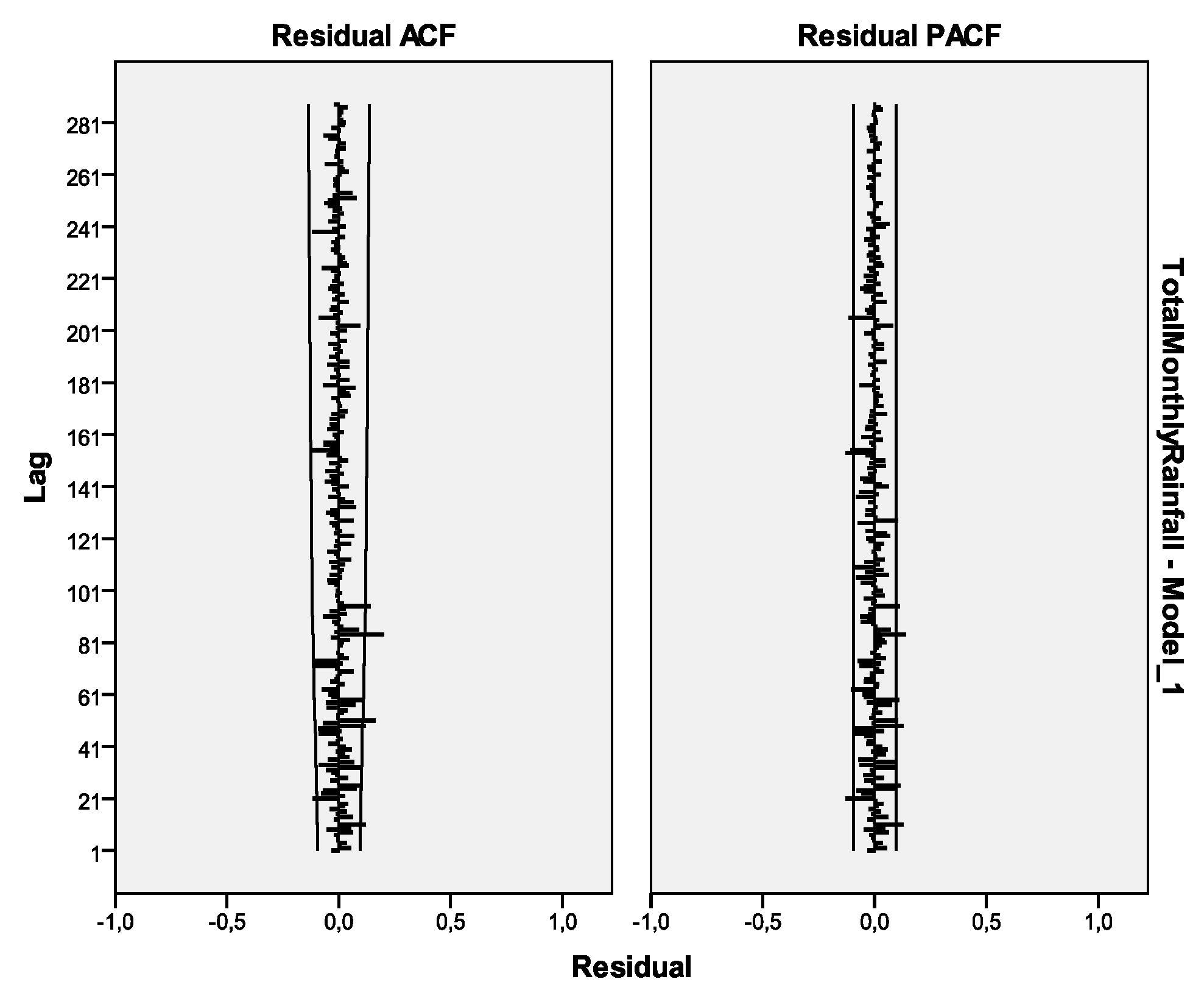
3.5. Model Adequacy and Diagnostic Tests
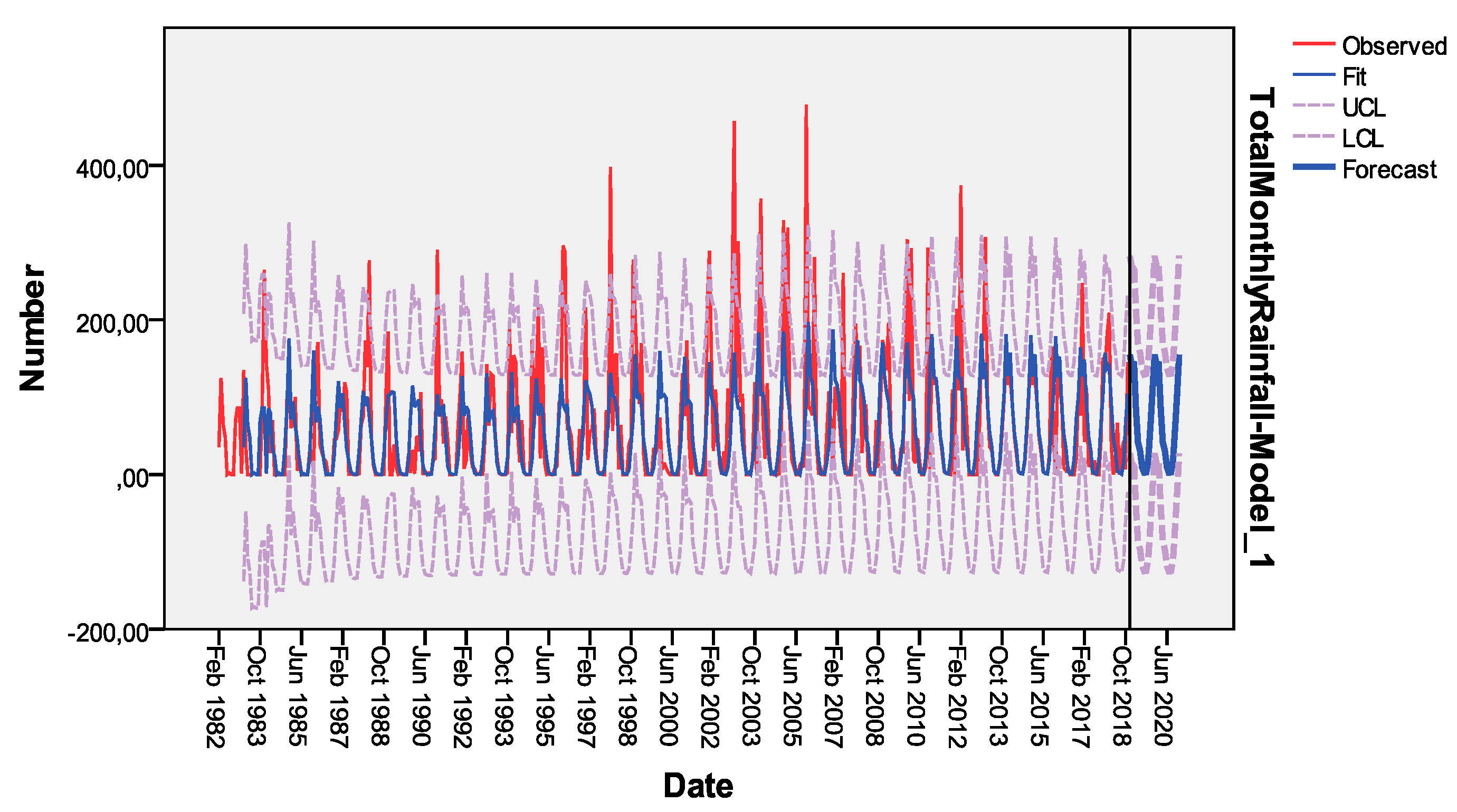
3.6. Forecasting Future Values
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Abdul-Aziz, A.R.; Anokye, M.; Kwame, A.; Munyakazi, L.; Nsowah-Nuamah, N.N.N. Modeling and forecasting rainfall pattern in ghana as a seasonal arima process: The case of ashanti region. Int. J. Humanit. Soc. Sci. 2013, 3, 224–233. Available online: https://www.researchgate.net/publication/306940437_Modeling_and_forecasting_rainfall_pattern_in_Ghana_as_a_seasonal_ARIMA_process_The_case_of_Ashanti_region (accessed on 3 March 2020).
- Bari, S.H.; Rahman, M.T.; Hussain, M.M.; Ray, S. Forecasting monthly precipitation in sylhet city using ARIMA model. Civ. Environ. Res. 2015, 7, 69–77. Available online: https://www.researchgate.net/publication/272744442_Forecasting_Monthly_Precipitation_in_Sylhet_City_Using_ARIMA_Model (accessed on 3 March 2020).
- Papalaskaris, T.; Panagiotidis, T.; Pantrakis, A. Stochastic monthly rainfall time series analysis, modeling and forecasting in Kavala city, Greece, North-Eastern Mediterranean basin. In Proceedings of the 2nd Efficient & Sustainable Water Systems Management toward Worth Living Development 2016 (2nd “E.W.a.S.” 2016), Platanias-Chania-Crete Island, Greece, 1–4 June 2016; Kanakoudis, V., Karatzas, G.P., Keramaris, E., Eds.; University of Thessaly: Volos, Greece; Technical University of Crete: Crete, Greece, 2016. [Google Scholar]
- Papalaskaris, T.; Panagiotidis, T.; Pantrakis, A. Stochastic monthly rainfall time series analysis, modeling and forecasting in Kavala city, Greece, North-Eastern Mediterranean basin. Procedia Eng. 2016, 162, 254–263. [Google Scholar] [CrossRef]
- Papalaskaris, T.; Panagiotidis, T. Stochastic monthly rainfall time series analysis, modeling and forecasting in Metaxades area, Evros, Greece, North-Eastern Mediterranean basin. In Proceedings of the 3rd Greek Conference of Civil Protection (“Employing New Technologies for Civil Protection Purposes”) 2016 (3rd “Safe Evros” 2016), Alexandroupoli (Evros prefecture), Greece, 22–25 June 2016; Maris, F.P., Ed.; Prefecture of Eastern Macedonia & Thrace, Democritus University of Thrace: Alexandroupolis, Greece, 2016; pp. 443–452. [Google Scholar]
- Papalaskaris, T.; Kampas, G. Time series analysis of water characteristics of streams in Eastern Macedonia-Thrace, Greece. Eur. Water 2017, 57, 93–100. Available online: https://www.ewra.net/ew/pdf/EW_2017_57_13.pdf (accessed on 3 March 2020).
- Papalaskaris, T.; Panagiotidis, T. Stochastic monthly rainfall time series analysis, modeling and forecasting in Karyes, Chios Island, Greece, Central-Eastern Mediterranean Basin. In Proceedings of the 15th International Conference on Environmental Sscience & Technology 2017 (15th “C.E.S.T.” 2017), Rhodes Island, Greece, 31 August–2 September 2017; Lekkas, D.F., Klontza, E., Vrentzou, K., Eds.; University of the Aegean: Mytilene Island, Greece ID 01008. [Google Scholar]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting & Control, Revised 5th ed.; John Wiley & Sons, Inc.: Hoboken, New Jersey, USA, 2015. [Google Scholar]

| ADF Unit Root Test | Number of Observations | Test Statistic | Interpolated Dickey-Fuller | Coefficients | |||
|---|---|---|---|---|---|---|---|
| Test Statistic (1% Critical Value) | Test Statistic (5% Critical Value) | Test Statistic (10% Critical Value) | L1 | _cons | |||
| Values | 444 | −14.754 | −3.445 | −2.872 | −2.570 | −0.6640124 | 41.09186 |
| SARIMA Model | Dec 2018 | Jan 2019 | Feb 2019 | Mar 2019 | Apr 2019 | May 2019 | Jun 2019 | Jul 2019 | Aug 2019 | Sep 2019 | Oct 2019 | Nov 2019 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Forecast | 155.02 | 140.41 | 145.67 | 87.15 | 41.61 | 30.31 | 9.24 | 2.26 | 2.80 | 18.07 | 61.07 | 107.78 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papalaskaris, T. Forecasting Monthly Rainfall of Karyes, Chios Island, Greece, Central-Eastern Mediterranean Basin Using the ARIMA Method. Environ. Sci. Proc. 2020, 2, 68. https://doi.org/10.3390/environsciproc2020002068
Papalaskaris T. Forecasting Monthly Rainfall of Karyes, Chios Island, Greece, Central-Eastern Mediterranean Basin Using the ARIMA Method. Environmental Sciences Proceedings. 2020; 2(1):68. https://doi.org/10.3390/environsciproc2020002068
Chicago/Turabian StylePapalaskaris, Thomas. 2020. "Forecasting Monthly Rainfall of Karyes, Chios Island, Greece, Central-Eastern Mediterranean Basin Using the ARIMA Method" Environmental Sciences Proceedings 2, no. 1: 68. https://doi.org/10.3390/environsciproc2020002068
APA StylePapalaskaris, T. (2020). Forecasting Monthly Rainfall of Karyes, Chios Island, Greece, Central-Eastern Mediterranean Basin Using the ARIMA Method. Environmental Sciences Proceedings, 2(1), 68. https://doi.org/10.3390/environsciproc2020002068




