Hydraulic Behavior Assessment of Type A and Type B Piano Key Weirs from Experimental and Numerical Results †
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Setup
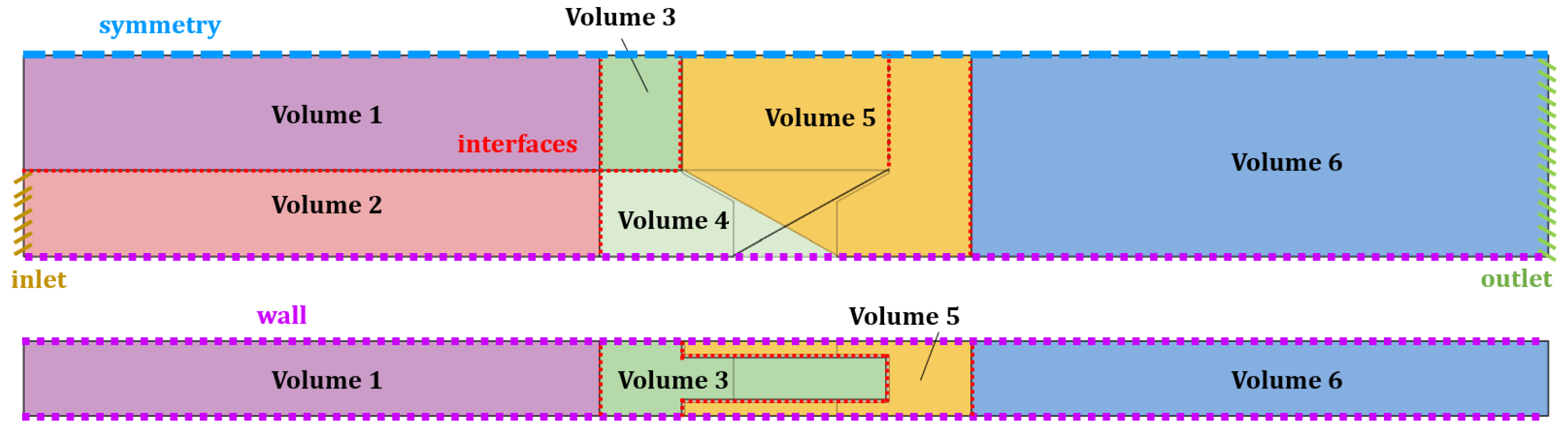
2.2. Numerical Model
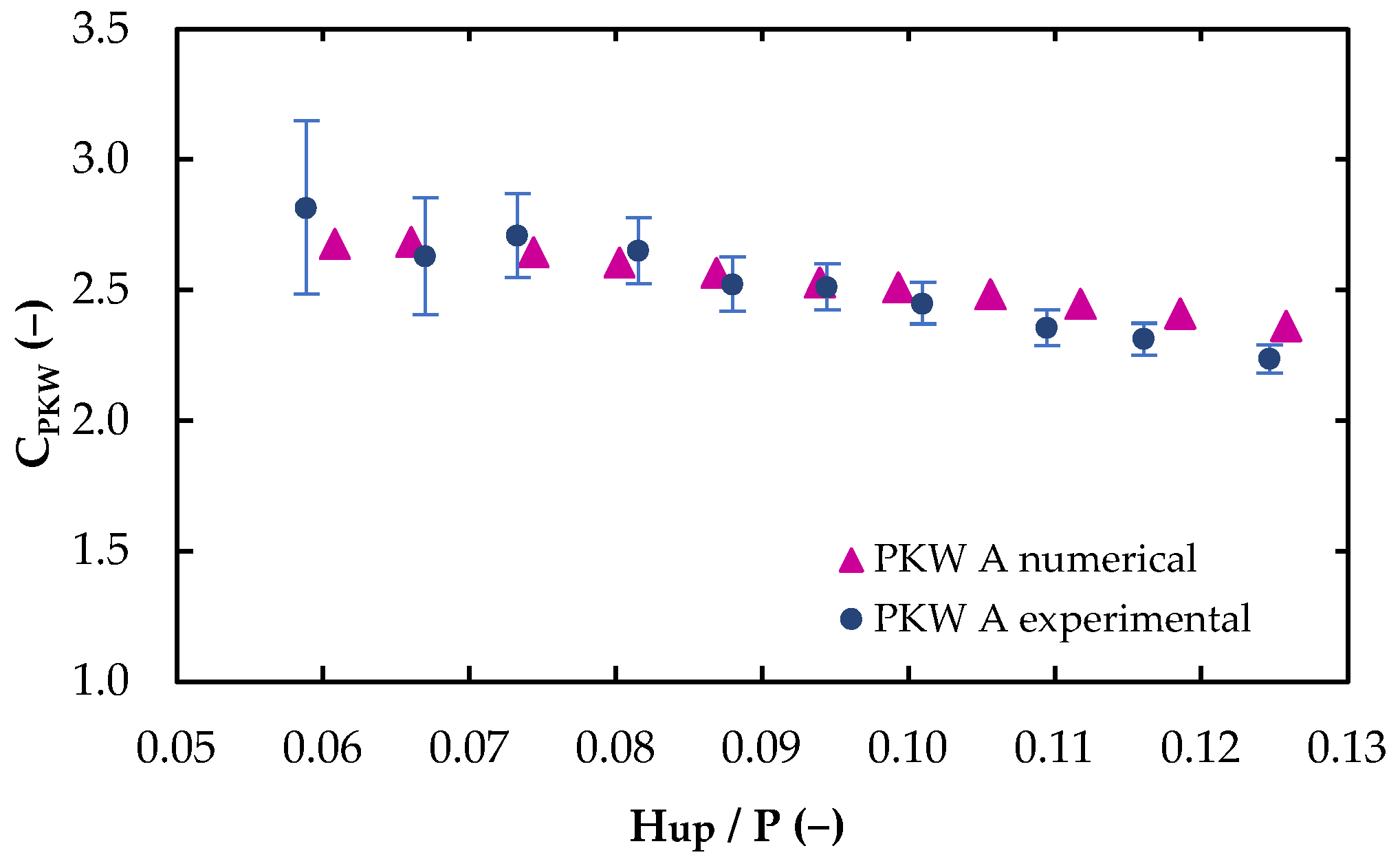
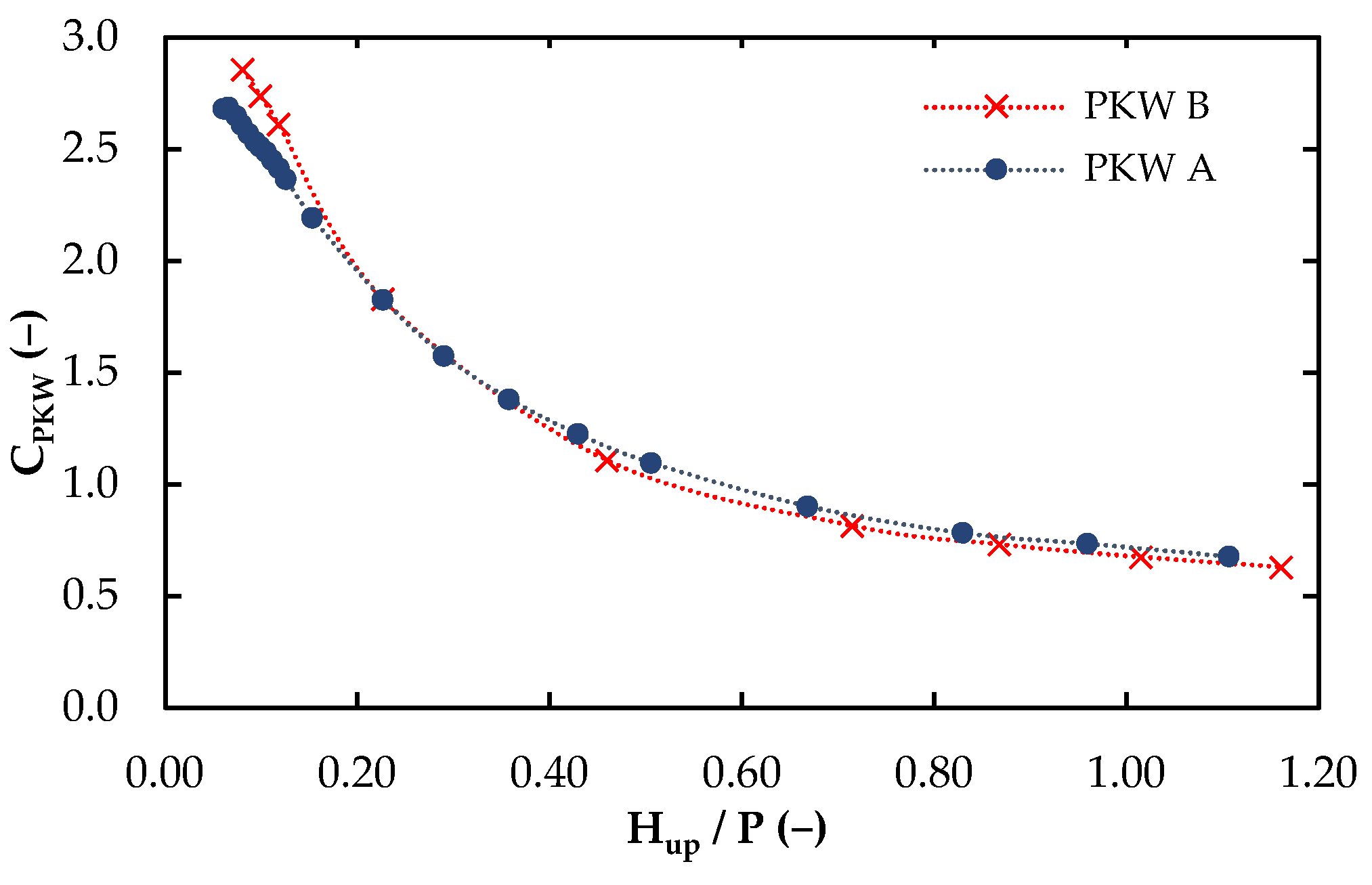
3. Results
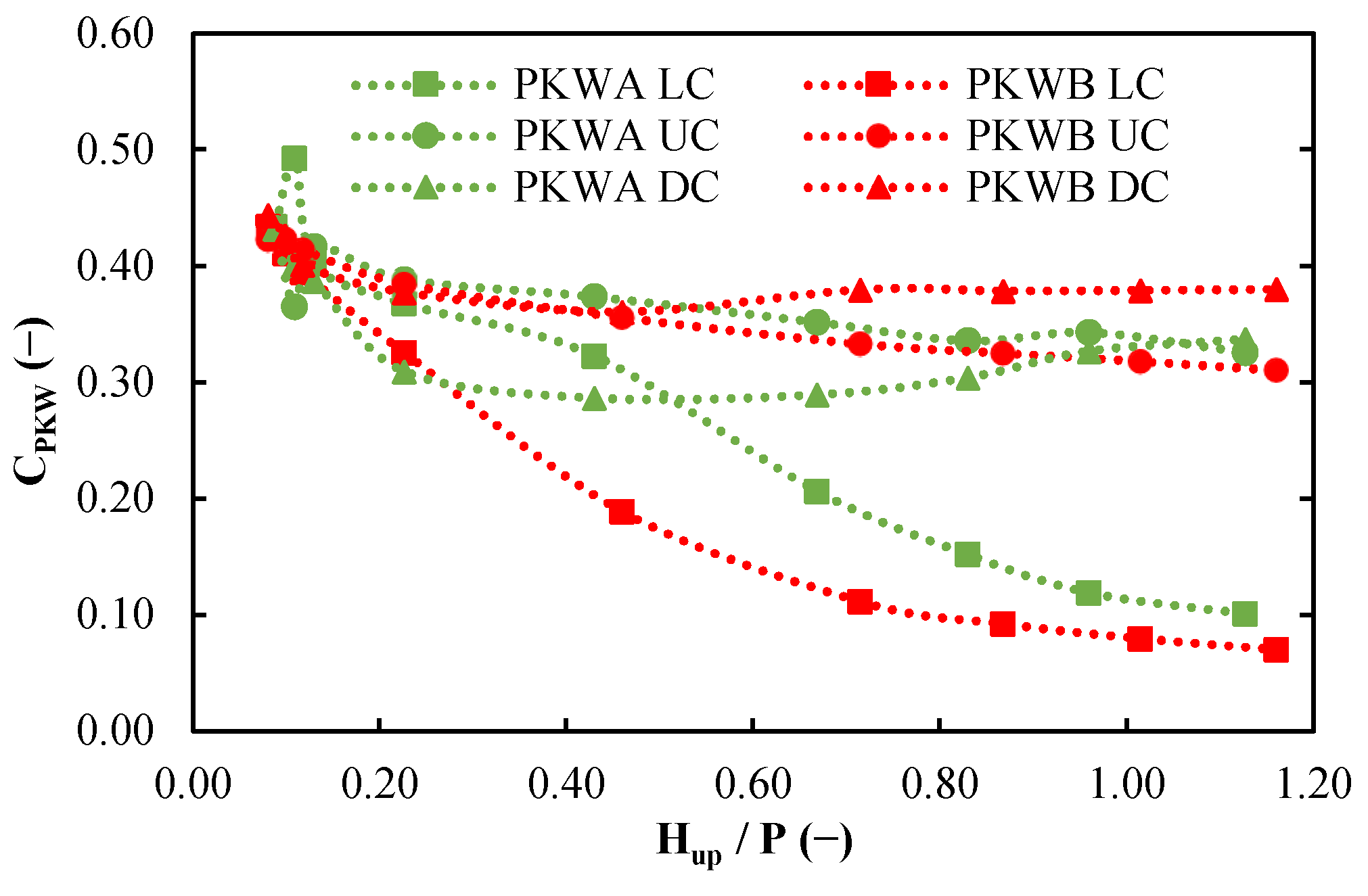
4. Discussion
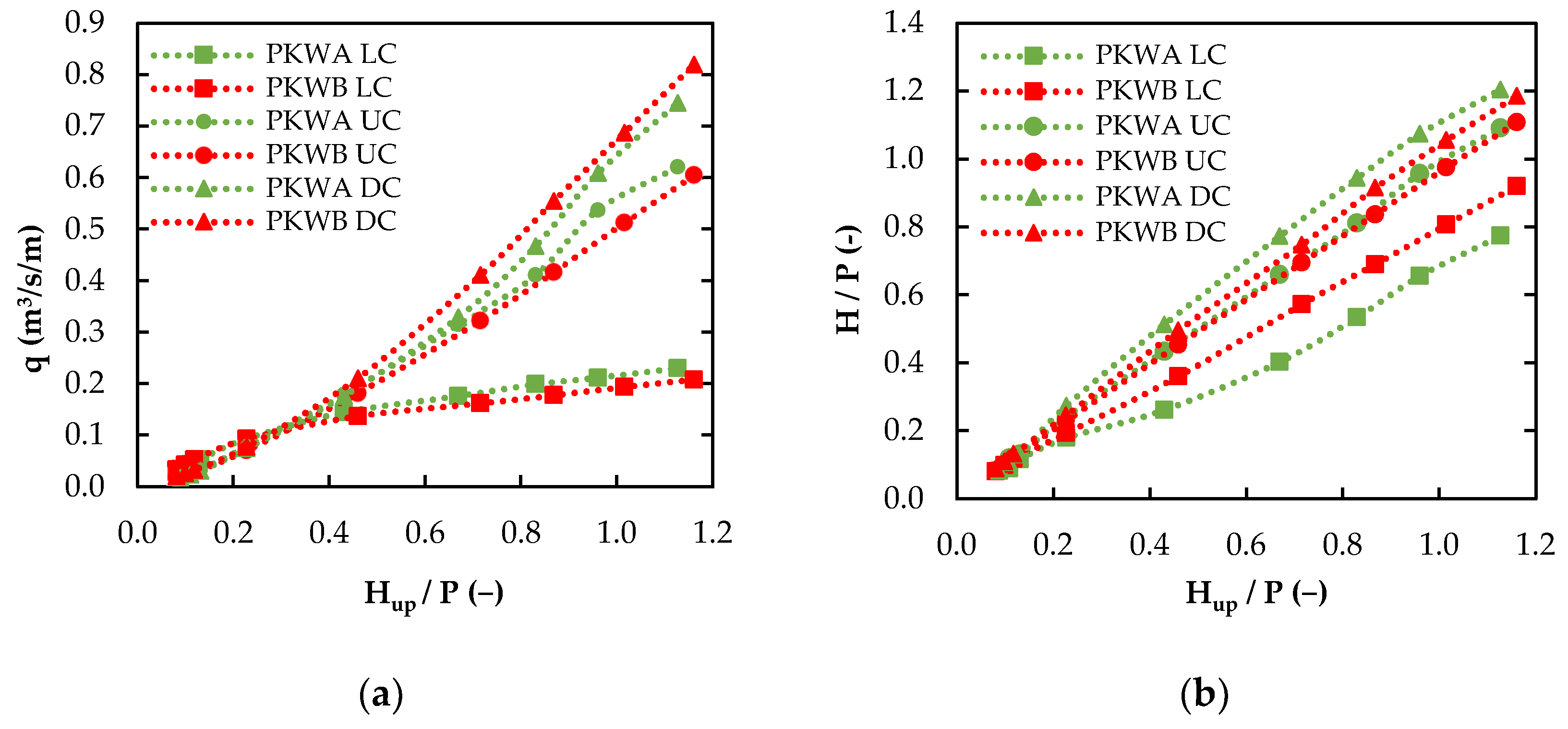
Discharge and Head Distribution over the Upstream, Downstream, and Lateral Crests
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lempérière, F.; Ouamane, A. The Piano Keys weir: A new cost-effective solution for spillways. Int. J. Hydropower Dams 2003, 10, 144–149. [Google Scholar]
- Pralong, J.; Vermeulen, J.; Blancher, B.; Laugier, F.; Erpicum, S.; Machiels, O.; Pirotton, M.; Boillat, J.; Ribeiro, M.; Schleiss, A. A naming convention for the Piano Key Weirs geometrical parameters. In Proceedings of the International Conference Labyrinth and Piano Key Weirs, Liège, Belgium, 9–11 February 2011; pp. 271–278. [Google Scholar] [CrossRef]
- Noui, A.; Ouamane, A. Study of optimization of the Piano key weir. In Proceedings of the International Conference Labyrinth and Piano Key Weirs–PKW, Liège, Belgium, 9–11 February 2011; pp. 175–182. [Google Scholar] [CrossRef]
- Pralong, J.; Montarros, F.; Blancher, B.; Laugier, F. A sensitivity analysis of Piano Key Weirs geometrical parameters based on 3D numerical modeling. In Proceedings of the International Conference Labyrinth and Piano Key Weirs–PKW, Liège, Belgium, 9–11 February 2011; pp. 133–139. [Google Scholar] [CrossRef]
- Ribeiro, M.; Boillat, J.; Schleiss, A.; Doucen, O.; Laugier, F. Experimental parametric study for hydraulic design of PKWs. In Proceedings of the International Conference on Labyrinth and Piano Key Weirs (PKW 2011), Liège, Belgium, 9–11 February 2011; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2011; pp. 183–190. [Google Scholar] [CrossRef]
- Machiels, O.; Erpicum, S.; Pirotton, M. Experimental analysis of PKW hydraulic performance and geometric parameters optimum. In Proceedings of the International workshop on Piano Key Weir for In-stream Storage and Dam Safety—PKWISD-2012, New Delhi, India, 30 May–1 June 2012. [Google Scholar]
- Anderson, R.M.; Tullis, B.P. Influence of Piano Key Weir geometry on discharge. In Proceedings of the Labyrinth and Piano Key Weirs—PKW 2011, Liège, Belgium, 9–11 February 2011; pp. 75–80. [Google Scholar]
- Lefebvre, V.; Vermeulen, J.; Blancher, B. Influence of geometrical parameters on pk-weirs discharge with 3d numerical analysis. In Proceedings of the 2nd International Workshop on Labyrinth and Piano Key Weirs 2013, Paris, France, 20–22 November 2013. [Google Scholar] [CrossRef]
- Machiels, O.; Pirotton, M.; Pierre, A.; Dewals, B.; Erpicum, S. Experimental parametric study and design of Piano Key Weirs. J. Hydraul. Res. 2014, 52, 326–335. [Google Scholar] [CrossRef]
- Bremer, F.; Oertel, M. Numerical investigation of wall thickness influence on Piano Key Weir discharge coefficients: A preliminary study. In Proceedings of the 3rd International Workshop on Labyrinth and Piano Key Weirs (PKW 2017), Qui Nhon, Vietnam, 22–24 February 2017; pp. 101–108. [Google Scholar] [CrossRef]
- Laugier, F.; Pralong, J.; Blancher, B. Influence of structural thickness of sidewalls on PKW spillway discharge capacity. In Proceedings of the International Conference on Labyrinth and Piano Key Weirs (PKW 2011), Liège, Belgium, 9–11 February 2011; pp. 159–165. [Google Scholar] [CrossRef]
- Erpicum, S.; Archambeau, P.; Dewals, B.; Pirotton, M. Hydraulics of Piano Key Weirs: A review. In Proceedings of the 3rd International Workshop on Labyrinth and Piano Key Weirs (PKW 2017), Qui Nhon, Vietnam, 22–24 February 2017; pp. 27–36. [Google Scholar]
- Cicero, G.; Delisle, J. Discharge characteristics of Piano Key weirs under submerged flow. In Proceedings of the second International Workshop on Labyrinth and Piano Key Weirs 2013, Paris, France, 20–22 November 2013; pp. 101–109. [Google Scholar]
- Machiels, O. Experimental Study of the Hydraulic Behaviour of Piano Key Weirs. Ph.D. Thesis, University of Liège, Liège, Belgium, 2012. [Google Scholar]
- Erpicum, S.; Tullis, B.P.; Lodomez, M.; Archambeau, P.; Dewals, B.J.; Pirotton, M. Scale effects in physical piano key weirs models. J. Hydraul. Res. 2016, 54, 692–698. [Google Scholar] [CrossRef]
- Abernethy, R.; Thompson, J.J. Uandbook, Uncertainty in Gas Turbine Measurements. In Proceedings of the 9th Propulsion Conference, Las Vegas, NV, USA, 5–7 November 1973. [Google Scholar]
- ANSYS Fluent 12.0 User’s Guide; Ansys Inc.: Washington County, PA, USA, 2019.
- Crookston, B.; Anderson, R.; Tullis, B. Free-flow discharge estimation method for Piano Key weir geometries. J. Hydro-Environ. Res. 2018, 19, 160–167. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J.; Coleman, H.; Raad, P.E. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluids Eng. Trans. ASME 2008, 130, 0780011–0780014. [Google Scholar] [CrossRef]
| PKW Parameter | Symbol | PKW Parameter | Symbol |
|---|---|---|---|
| Inlet Height | Pi | Inlet Width | Wi |
| Outlet Height | Po | Outlet Width | Wo |
| Height of the base | Pb | Wall thickness | Ts |
| Crest height | P | Inlet Slope | Si |
| Total Lateral Length | B | Outlet Slope | So |
| Outlet Length | Bo | Unit Width | Wu = Wi + Wo + 2·Ts |
| Inlet Length | Bi | Unit Length | Lu = 2·Bh + Wu |
| Length of the base | Bb | Total developed length | L = Nu·Lu |
| Number of units | Nu | Total width of the PKW | W = Nu·Wu |
| P | 0.522 m | Wi | 0.255 m |
| B | 1.254 m | Wo | 0.170 m |
| Bo | 0.628 m | Wu | 0.455 m |
| Bi | 0 m | Lu | 2.963 m |
| Bb | 0.626 m | Ts | 0.15 m |
| PKWA | Bo = 0.314 m; Bi = 0.314 m | ||
| PKWB | Bo = 0.628 m; Bi = 0 m | ||
| Mesh | Volume | Number of Cells | Computational Time | |||
|---|---|---|---|---|---|---|
| 3 | 4 | 5 | 6 | |||
| h1 | 2.0 cm | 3.0 cm | 2.0 cm | inflation of 2.0 cm | 696,799 | ∼4 days |
| h2 | 1.5 cm | 2.0 cm | 1.5 cm | inflation of 1.5 cm | 1,521,601 | ∼10 days |
| h3 | 1.15 cm | 1.3 cm | 1.15 cm | inflation of 1.15 cm | 3,569,820 | ∼25 days |
| h4 | 0.8 cm | 1.0 cm | 0.8 cm | inflation of 0.8 cm | 9,503,531 | ∼40 days |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torre-Gómez, G.; Erpicum, S.; Pugliese, F.; Giugni, M. Hydraulic Behavior Assessment of Type A and Type B Piano Key Weirs from Experimental and Numerical Results. Environ. Sci. Proc. 2022, 21, 84. https://doi.org/10.3390/environsciproc2022021084
Torre-Gómez G, Erpicum S, Pugliese F, Giugni M. Hydraulic Behavior Assessment of Type A and Type B Piano Key Weirs from Experimental and Numerical Results. Environmental Sciences Proceedings. 2022; 21(1):84. https://doi.org/10.3390/environsciproc2022021084
Chicago/Turabian StyleTorre-Gómez, Guadalupe, Sebastien Erpicum, Francesco Pugliese, and Maurizio Giugni. 2022. "Hydraulic Behavior Assessment of Type A and Type B Piano Key Weirs from Experimental and Numerical Results" Environmental Sciences Proceedings 21, no. 1: 84. https://doi.org/10.3390/environsciproc2022021084
APA StyleTorre-Gómez, G., Erpicum, S., Pugliese, F., & Giugni, M. (2022). Hydraulic Behavior Assessment of Type A and Type B Piano Key Weirs from Experimental and Numerical Results. Environmental Sciences Proceedings, 21(1), 84. https://doi.org/10.3390/environsciproc2022021084










