A Background Error Statistics Analysis over the Mediterranean: The Impact on 3DVAR Data Assimilation †
Abstract
:1. Introduction
2. Materials and Methods
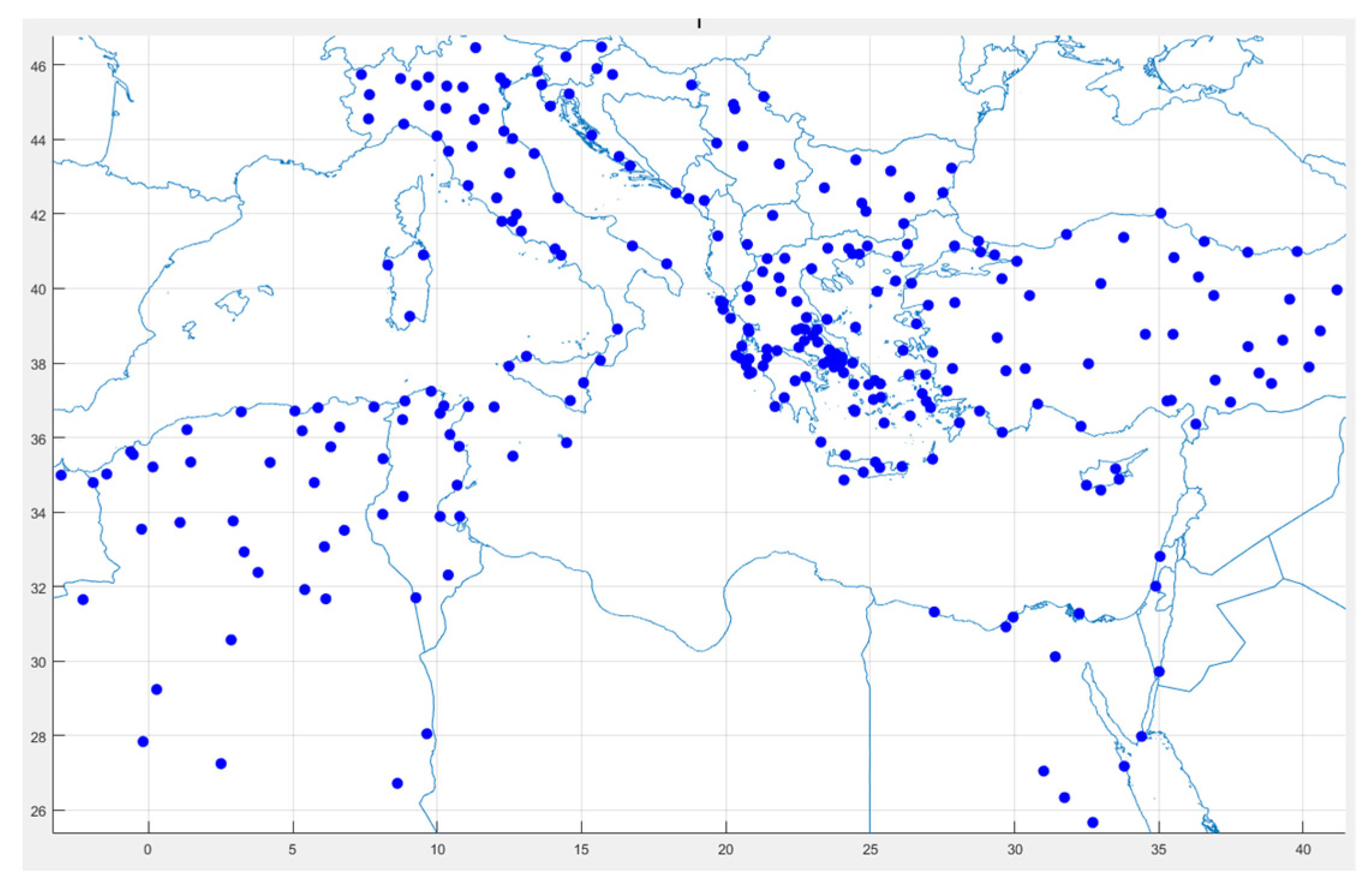
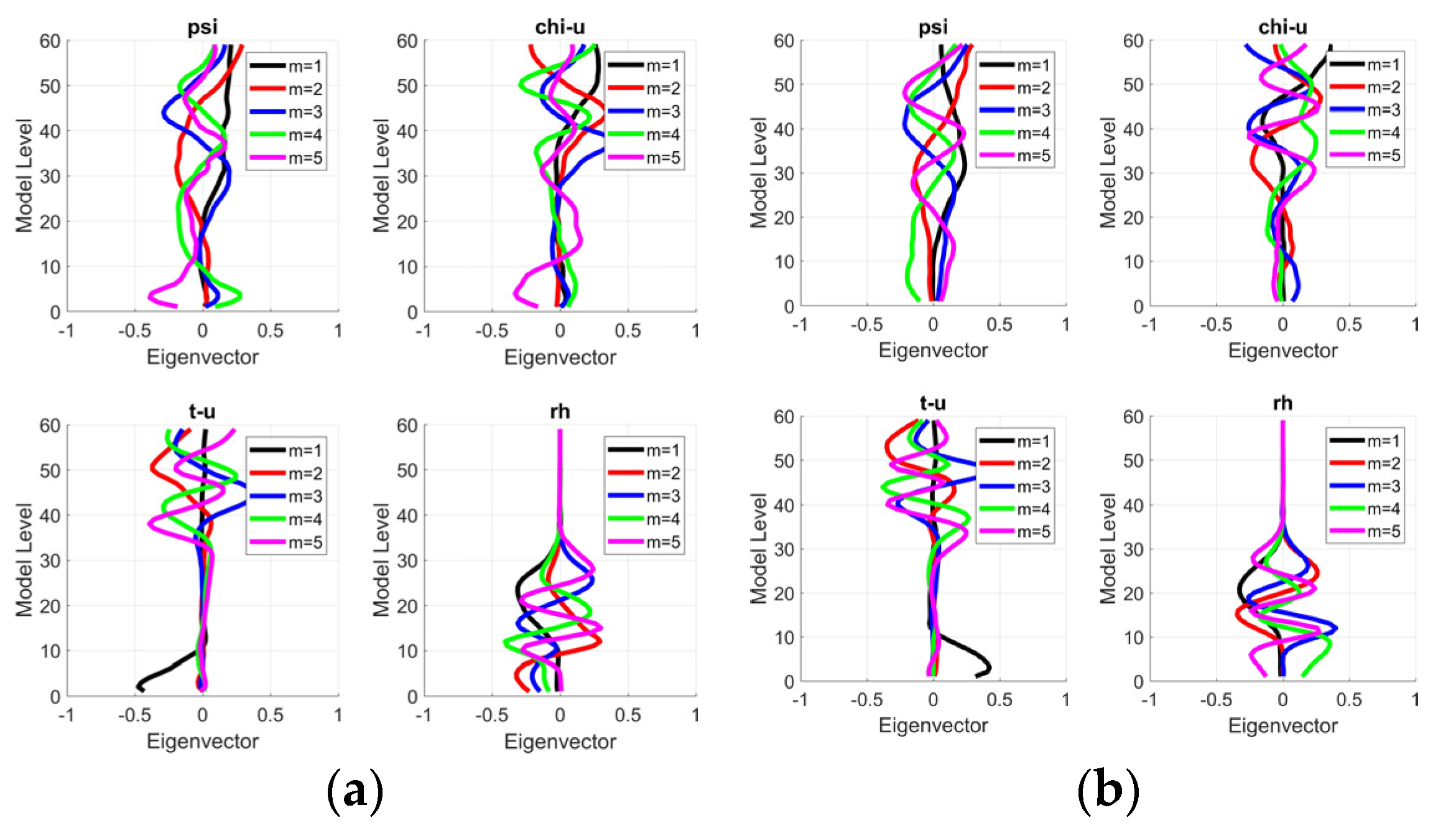
2.1. BE Estimates
2.2. Data Assimilation
2.3. WRF Configuration and Runs
3. Results
3.1. BE Results
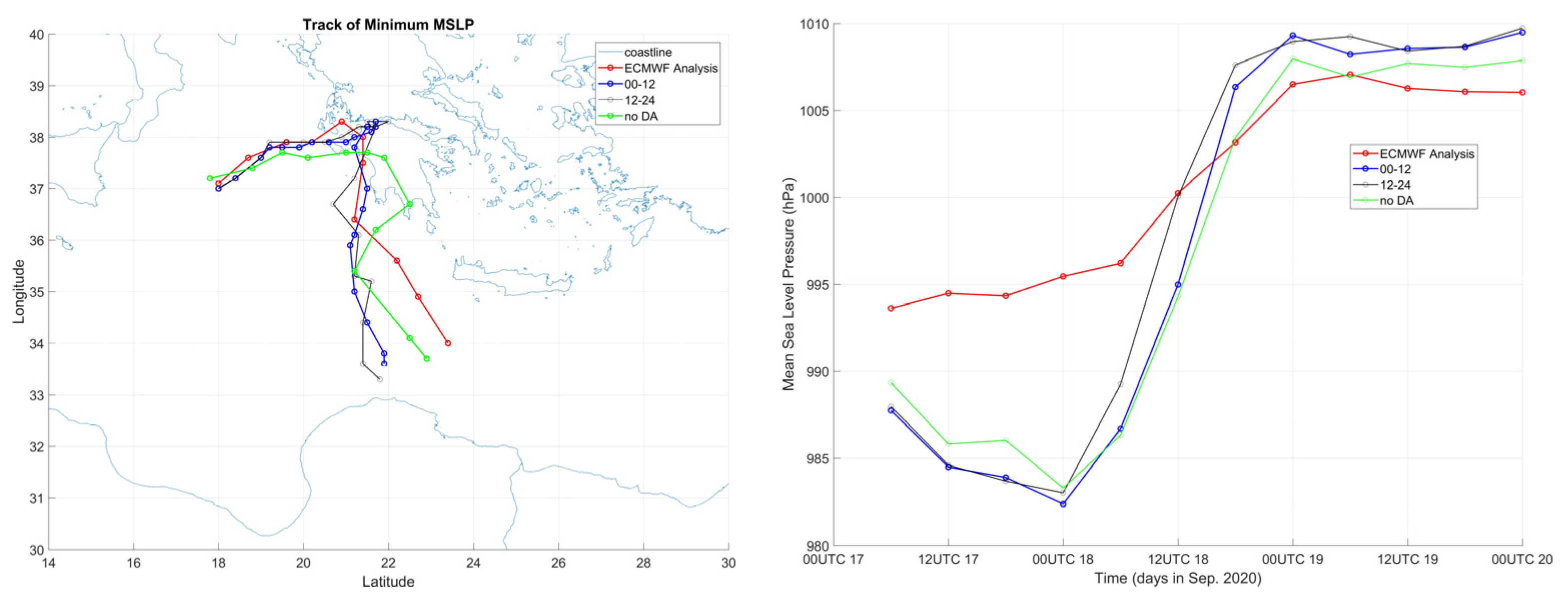
3.2. Temperature Difference of BE1 and BE2 Runs
3.3. Track and Intensity of BE1 and BE2 Runs
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, J.; Bray, M.; Han, D. Exploring the effect of data assimilation by WRF-3DVar for numerical rainfall prediction with different types of storm events. Hydrol. Process. 2013, 27, 3627–3640. [Google Scholar] [CrossRef]
- Xiong, C.-H.; Zhang, L.-F.; Guan, J.-P.; Peng, J.; Zhang, B. Analysis and numerical study of a hybrid BGM-3DVAR data assimilation scheme using satellite radiance data for heavy rain forecasts. J. Hydrodyn. 2013, 25, 430–439. [Google Scholar] [CrossRef]
- Barker, D.M.; Huang, W.; Guo, Y.-R.; Bourgeois, A.J.; Xiao, Q.N. A Three-Dimensional Variational Data Assimilation System for MM5: Implementation and Initial Results. Mon. Weather Rev. 2004, 132, 897–914. [Google Scholar] [CrossRef]
- Xiao, Q.; Sun, J. Multiple-Radar Data Assimilation and Short-Range Quantitative Precipitation Forecasting of a Squall Line Observed during IHOP_2002. Mon. Weather Rev. 2007, 135, 3381–3404. [Google Scholar] [CrossRef]
- Lindskog, M.; Gustafsson, N.; Mogensen, K.S. Representation of background error standard deviations in a limited area model data assimilation system. Tellus A Dyn. Meteorol. Oceanogr. 2006, 58, 430–444. [Google Scholar] [CrossRef]
- Hacker, J.P.; Rostkier-Edelstein, D. PBL state estimation with surface observations, a column model, and an ensemble filter. Mon. Weather Rev. 2007, 135, 2958–2972. [Google Scholar] [CrossRef]
- Stensrud, D.J.; Yussouf, N.; Dowell, D.C.; Coniglio, M.C. Assimilating surface data into a mesoscale model ensemble: Cold pool analyses from spring 2007. Atmos. Res. 2009, 93, 207–220. [Google Scholar] [CrossRef]
- Ruggiero, F.H.; Modica, G.D.; Lipton, A.E. Assimilation of Satellite Imager Data and Surface Observations to Improve Analysis of Circulations Forced by Cloud Shading Contrasts. Mon. Weather Rev. 2000, 128, 434. [Google Scholar] [CrossRef]
- Parrish, D.F.; Derber, J.C. The National Meteorological Center’s Statistical Spectral Interpolation Analysis System. Mon. Weather Rev. 1992, 109, 1747–1763. [Google Scholar] [CrossRef]
- Kutaladze, N.; Mikuchadze, G. Background Error in WRF Model. WSEAS Trans. Environ. Dev. 2020, 16, 619–624. [Google Scholar] [CrossRef]
- Gustafsson, N.; Janjić, T.; Schraff, C.; Leuenberger, D.; Weissmann, M.; Reich, H.; Brousseau, P.; Montmerle, T.; Wattrelot, E.; Bučánek, A.; et al. Survey of data assimilation methods for convective-scale numerical weather prediction at operational centres. Q. J. R. Meteorol. Soc. 2018, 144, 1218–1256. [Google Scholar] [CrossRef]
- Lee, J.C.K.; Huang, X.-Y. Background error statistics in the Tropics: Structures and impact in a convective-scale numerical weather prediction system. Q. J. R. Meteorol. Soc. 2020, 146, 2154–2173. [Google Scholar] [CrossRef]
- Wang, H.; Huang, X.-Y.; Xu, D.; Liu, J. A scale-dependent blending scheme for WRFDA: Impact on regional weather forecasting. Geosci. Model Dev. 2014, 7, 1819–1828. [Google Scholar] [CrossRef]
- Lorenc, A.C. Analysis methods for numerical weather prediction. Q. J. R. Meteorol. Soc. 1966, 112, 1177–1194. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samos, I.; Flocas, H.; Louka, P. A Background Error Statistics Analysis over the Mediterranean: The Impact on 3DVAR Data Assimilation. Environ. Sci. Proc. 2023, 26, 158. https://doi.org/10.3390/environsciproc2023026158
Samos I, Flocas H, Louka P. A Background Error Statistics Analysis over the Mediterranean: The Impact on 3DVAR Data Assimilation. Environmental Sciences Proceedings. 2023; 26(1):158. https://doi.org/10.3390/environsciproc2023026158
Chicago/Turabian StyleSamos, Ioannis, Helena Flocas, and Petroula Louka. 2023. "A Background Error Statistics Analysis over the Mediterranean: The Impact on 3DVAR Data Assimilation" Environmental Sciences Proceedings 26, no. 1: 158. https://doi.org/10.3390/environsciproc2023026158
APA StyleSamos, I., Flocas, H., & Louka, P. (2023). A Background Error Statistics Analysis over the Mediterranean: The Impact on 3DVAR Data Assimilation. Environmental Sciences Proceedings, 26(1), 158. https://doi.org/10.3390/environsciproc2023026158







