Aerodynamics of Flight Formations in Birds: A Quest for Energy Efficiency
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Geometric Setup and Computational Framework
2.2. Boundary Conditions
2.3. Computational Mesh
2.4. Methods for Real-Time Mesh Adaptation
2.5. Computational Approaches
3. Results
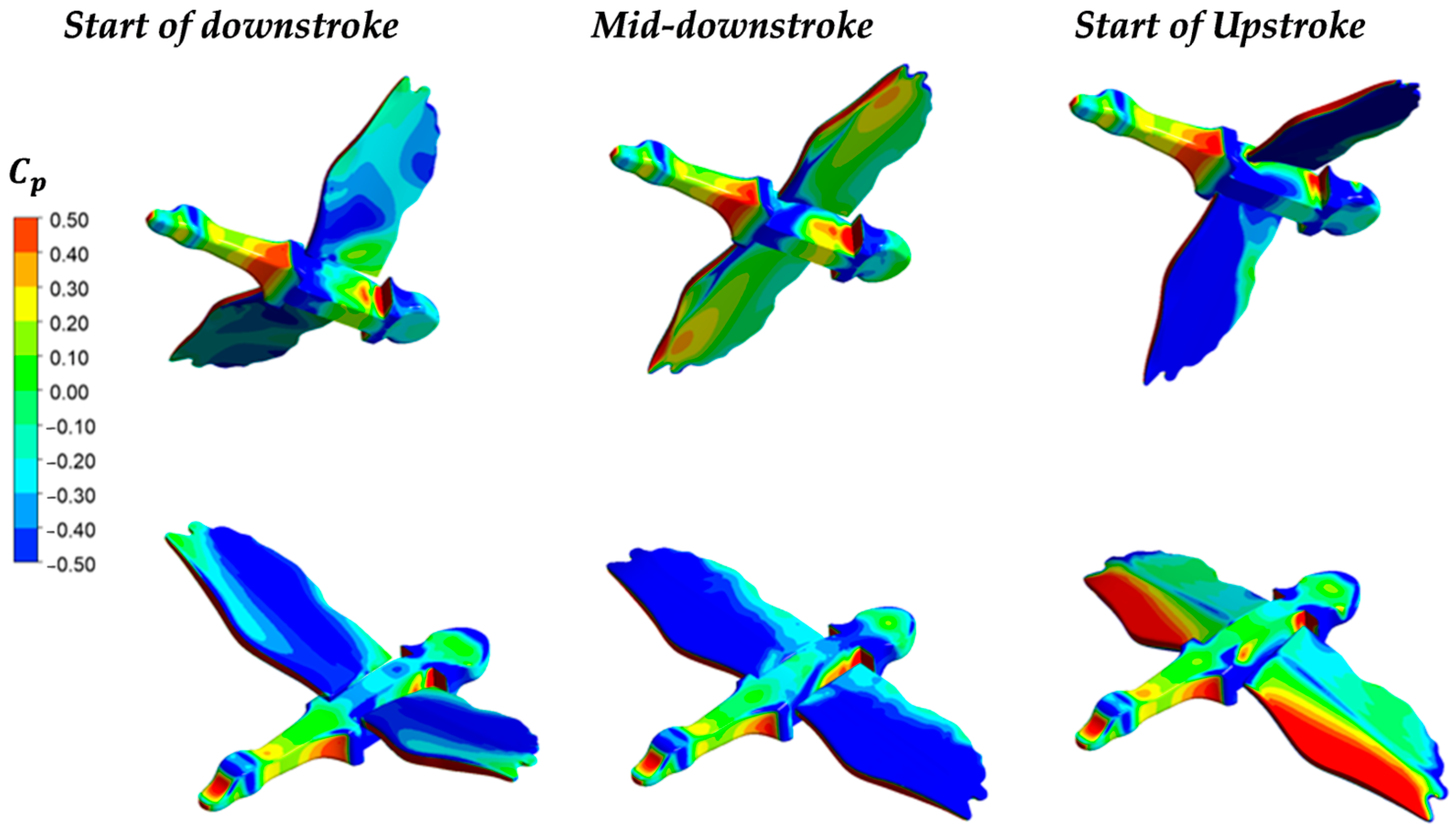
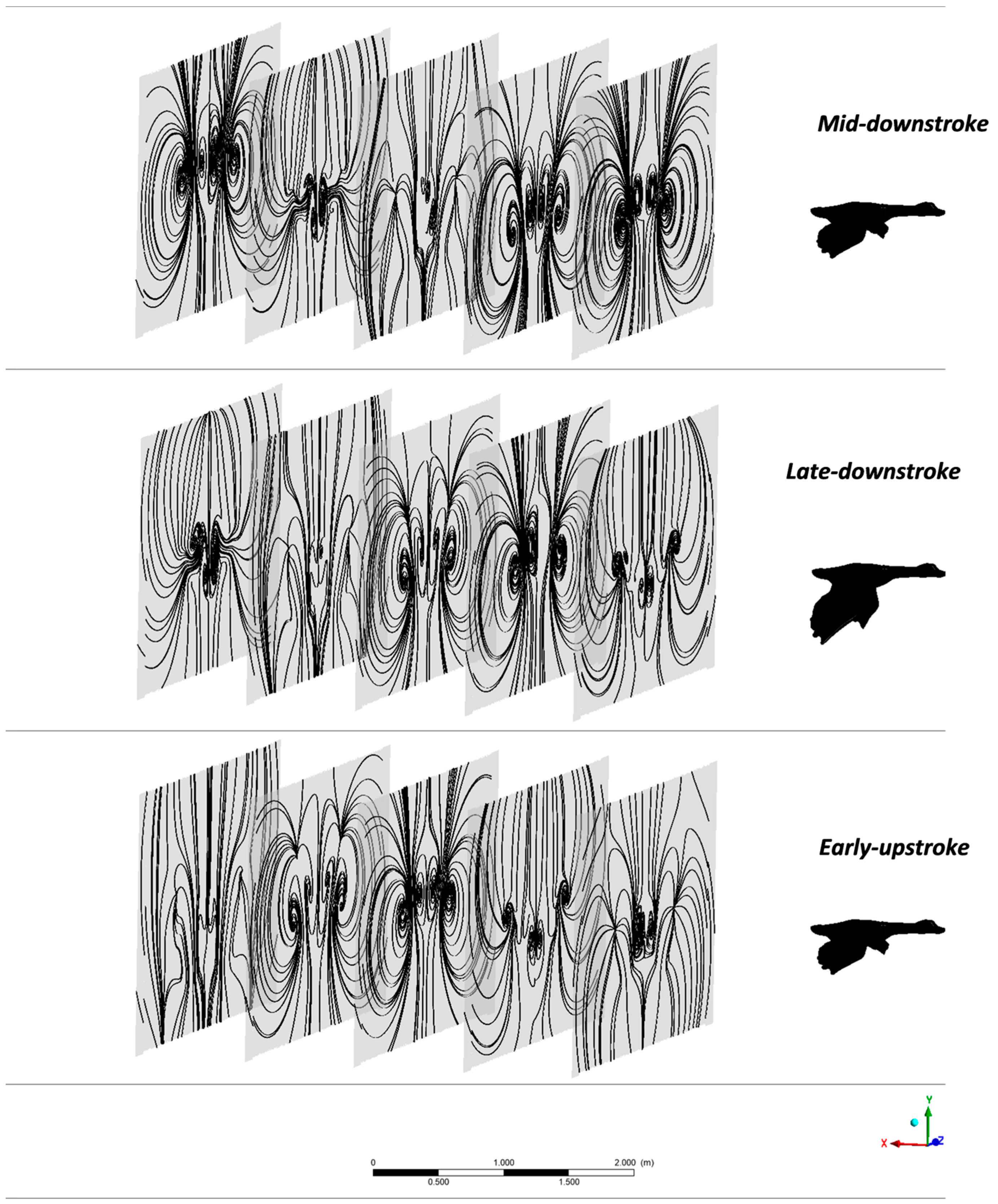
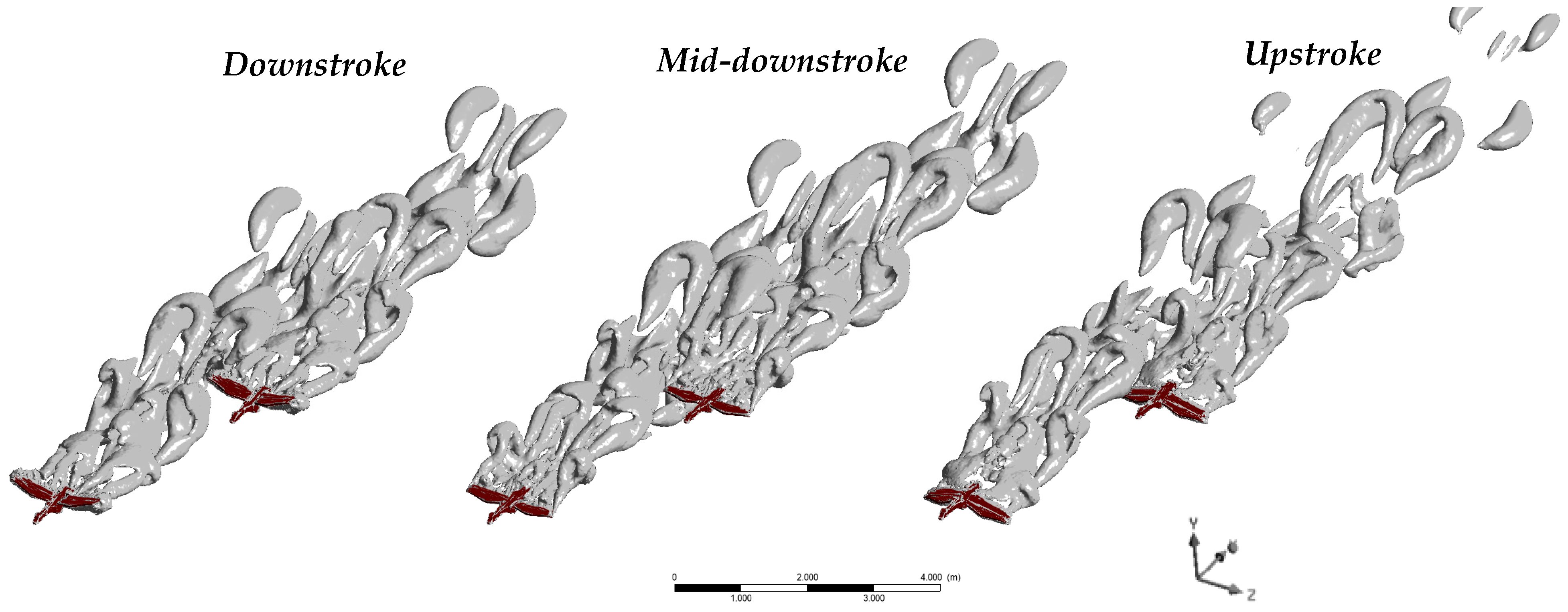
3.1. Aerodynamic Performance of a Lone Bird in Flight
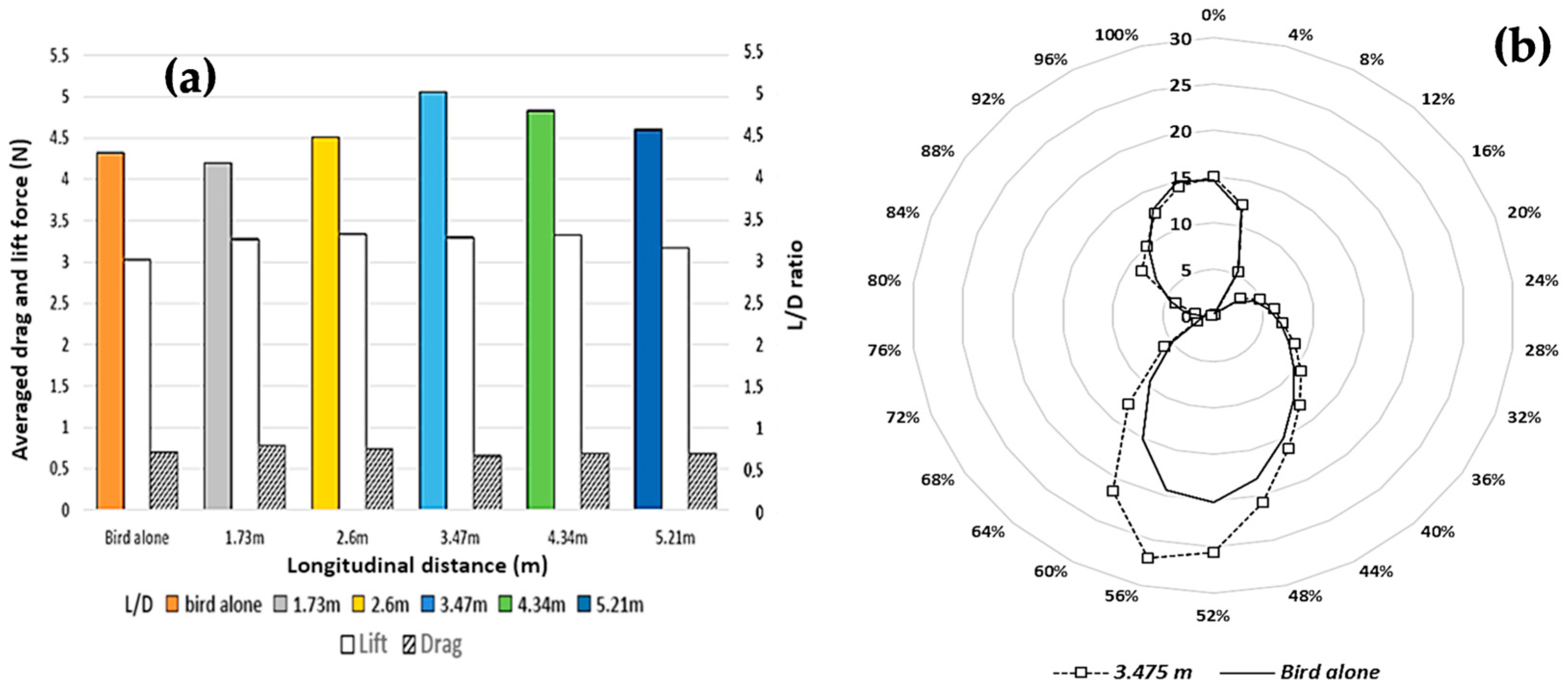
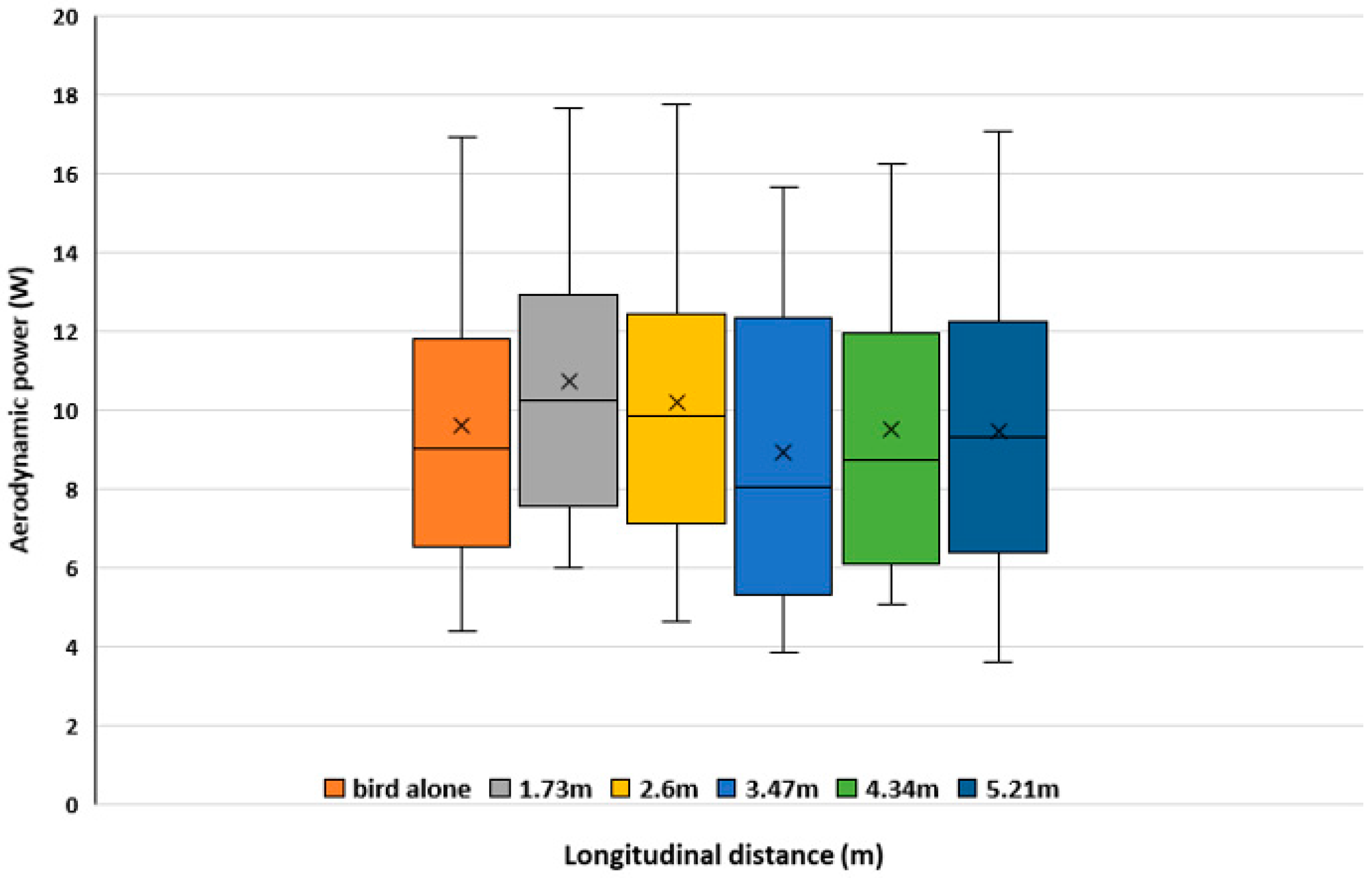
3.2. Aerodynamic Interactions Between Two Birds Flying in Formation
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Beaumont, F.; Murer, S.; Bogard, F.; Polidori, G. The Aerodynamic Mechanisms of the Formation Flight of Migratory Birds: A Narrative Review. Appl. Sci. 2024, 14, 5402. [Google Scholar] [CrossRef]
- Couzin, I.D.; Krause, J.; Franks, N.R.; Levin, S.A. Effective Leadership and Decision Making in Animal Groups on the Move. Nature 2004, 433, 513–516. [Google Scholar]
- Nagy, M.; Akos, Z.; Biro, D.; Vicsek, T. Hierarchical group dynamics in pigeon flocks. Nature 2010, 464, 890–894. [Google Scholar]
- May, R.M. Flight formations in Geese and other birds. Nature 1979, 282, 778–780. [Google Scholar]
- Lissaman, P.B.; Schollenberger, C.A. Formation flight of birds. Science 1970, 168, 1003–1005. [Google Scholar] [PubMed]
- Badgerow, J.P.; Hainsworth, F.R. Energy Savings through Formation Flight? A Reexamination of the Vee Formation. J. Theor. Biol. 1981, 93, 41–52. [Google Scholar]
- Cutts, C.J.; Speakman, J.R. Energy Savings in Formation Flight of Pink-Footed Geese. J. Exp. Biol. 1994, 189, 251–261. [Google Scholar]
- Hummel, D. Aerodynamic aspects of formation flight in birds. J. Theor. Biol. 1983, 104, 321–347. [Google Scholar]
- Liao, J.C.; Beal, D.N.; Lauder, G.V.; Triantafyllou, M.S. Fish exploiting vortices decrease muscle activity. Science 2003, 302, 1566–1569. [Google Scholar]
- Bill, R.G.; Hernnkind, W.F. Drag Reduction by Formation Movement in Spiny Lobsters. Science 1976, 193, 1146–1148. [Google Scholar]
- Weimerskirch, H.; Martin, J.; Clerquin, Y.; Alexandre, P.; Jiraskova, S. Energy saving in flight formation. Nature 2001, 413, 697–698. [Google Scholar] [PubMed]
- Fish, F.E. Kinematics of ducklings swimming in formation: Consequence of position. J. Exp. Zool. 1995, 273, 1–11. [Google Scholar] [CrossRef]
- Speakman, J.R.; Banks, D. The function of flight formation in Greylag geese (Anser anser): Energy saving or orientation? Ibis 1998, 140, 280–287. [Google Scholar]
- Chichka, D.F.; Speyer, J.L.; Park, C.G. Peek-Seeking Control with Application to Formation Flight. In Proceedings of the 38th IEEE Conference on Decision and Control (Cat. No. 99CH36304), Phoenix, AZ, USA, 7–10 December 1999; pp. 2463–2470. [Google Scholar]
- Andersson, M.; Wallander, J. Kin Selection and Reciprocity in Flight Formation? Behav. Ecol. 2004, 15, 158–162. [Google Scholar]
- Higdon, J.; Corrsin, S. Induced drag of a bird flock. Am. Nat. 1978, 112, 727–744. [Google Scholar]
- Badgerow, J. An Analysis of Function in the Formation Flight of Canada Geese. Auk 1988, 93, 41–52. [Google Scholar]
- Gould, L.L.; Heppner, F. The vee formation of Canada Geese. Auk 1974, 91, 494–506. [Google Scholar]
- Heppner, F.; Convissar, J.; Moonan, D.E., Jr.; Anderson, J. Visual angle and formation flight in Canada geese (Branta canadensis). Auk 1985, 102, 195–198. [Google Scholar] [CrossRef]
- Biewener, A.A. Biomechanics of Avian Flight. Curr. Biol. 2022, 32, R1110–R1114. [Google Scholar] [CrossRef]
- Rayner, J. A vortex theory of animal flight. Part 2. The forward flight of birds. J. Fluid. Mech. 1979, 91, 731–763. [Google Scholar] [CrossRef]
- Magnan, A.; Perrilliat-Botonet, C.; Girerd, H. Essais d’enregistrements cinématographiques simultanées dans trois directions perpendiculaires deux à deux de l’écoulement de l’air autour d’un oiseau en vol. C. R. Acad. Sci. Paris 1938, 206, 462–464. [Google Scholar]
- Chizhikova, S.; Mendez, L.X.; Hedrick, T.L. Behavior and Biomechanics: Flapping Frequency during Tandem and Solo Flights of Cliff Swallows. J. Exp. Biol. 2025, 228, jeb249393. [Google Scholar] [CrossRef]
- Spedding, G.R.; Rosén, M.; Hedenström, A. A family of vortex wakes generated by a thrush nightingale in free flight in a wind tunnel over its entire natural range of flight speeds. J. Exp. Biol. 2003, 206, 2313–2344. [Google Scholar] [CrossRef]
- Nafi, A.S.; Ben-Gida, H.; Guglielmo, C.G.; Gurka, R. Aerodynamic forces acting on birds during flight: A comparative study of a shorebird, songbird, and a strigiform. Exp. Therm. Fluid Sci. 2020, 113, 110018. [Google Scholar] [CrossRef]
- Michael, D. Animal locomotion: A new spin on bat flight. Curr. Biol. 2008, 18, 468–470. [Google Scholar]
- Maeng, J.S.; Park, J.H.; Min Jang, S.; Han, S.Y. A modeling approach to energy savings of flying Canada Geese using computational fluid dynamics. J. Theor. Biol. 2013, 320, 76–85. [Google Scholar] [PubMed]
- Song, J.; Tobalske, B.W.; Powers, D.R.; Hedrick, T.L.; Luo, H. Three-dimensional simulation for fast forward flight of a calliope hummingbird. R. Soc. Open Sci. 2016, 3, 160230. [Google Scholar]
- Beaumont, F.; Murer, S.; Bogard, F.; Polidori, G. Aerodynamic Interaction of Migratory Birds in Gliding Flight. Fluids 2023, 8, 50. [Google Scholar] [CrossRef]
- Liu, T.; Kuykendoll, K.; Rhew, R.D.; Jones, S. Avian Wings. In Proceedings of the 24th AIAA Aerodynamic Measurement Technology and Ground Testing Conference, Portland, OR, USA, 28 June–1 July 2004; AIAA Paper: Reston, VA, USA, 2004; pp. 2004–2186. [Google Scholar]
- Dimitriadis, G.; Gardiner, J.D.; Tickle, P.G.; Codd, J.; Nudds, R.L. Experimental and Numerical Study of the Flight of Geese. Aeronaut. J. 2015, 119, 803–832. [Google Scholar] [CrossRef]
- Mirzaeinia, A.; Heppner, F.; Hassanalian, M. An Analytical Study on Leader and Follower Switching in V-Shaped Canada Goose Flocks for Energy Management Purposes. Swarm Intell. 2020, 14, 117–141. [Google Scholar] [CrossRef]
- Withers, P.C. An Aerodynamic Analysis of Bird Wings as Fixed Aerofoils. J. Exp. Biol. 1981, 90, 143–162. [Google Scholar] [CrossRef]
- Blocken, B. Computational Fluid Dynamics for Urban Physics: Importance, Scales, Possibilities, Limitations, and Ten Tips and Tricks Towards Accurate and Reliable Simulations. Build. Environ. 2015, 91, 219–245. [Google Scholar] [CrossRef]
- Tucker, V.A.; Schmidt-Koenig, K. Flight speeds of birds in relation to energetics and wind directions. Auk 1971, 88, 97–107. [Google Scholar] [CrossRef]
- Fergus, C. Canada Goose. In Wildlife Notes-20, LDR0103; Pennsylvania Game Commission: Harrisburg, PA, USA, 2010. [Google Scholar]
- Funk, G.D.; Milsom, W.K.; Steeves, J.D. Coordination of Wingbeat and Respiration in the Canada Goose. I. Passive Wing Flapping. J. Appl. Physiol. 1985, 73, 1014–1024. [Google Scholar] [CrossRef]
- Beaumont, F.; Murer, S.; Bogard, F.; Polidori, G. Aerodynamics of a Flapping Wing as a Function of Altitude: New Insights into the Flight Strategy of Migratory Birds. Phys. Fluids 2021, 33, 127118. [Google Scholar] [CrossRef]
- Su, J.-Y.; Tang, J.-H.; Wang, C.-H.; Yang, J.-T. A Numerical Investigation on the Ground Effect of a Flapping-Flying Bird. Phys. Fluids 2013, 25, 093101. [Google Scholar] [CrossRef]
- Menter, F.R. Zonal two-equation k-ω turbulence model for aerodynamic flows. In Proceedings of the 23rd Fluid Dynamics, Plasmadynamics, and Lasers Conference, Orlando, FL, USA, 6–9 July 1993; AIAA Paper: Reston, VA, USA, 1993; pp. 1993–2906. [Google Scholar]
- Liu, T.; Wang, S.; Liu, H.; He, G. Engineering Perspective on Bird Flight: Scaling, Geometry, Kinematics and Aerodynamics. Prog. Aerosp. Sci. 2023, 142, 100933. [Google Scholar] [CrossRef]
- Beaumont, F.; Murer, S.; Bogard, F.; Polidori, G. Aerodynamic Mechanisms behind Energy Efficiency in Migratory Bird Formations. Phys. Fluids 2025, 37, 025202. [Google Scholar] [CrossRef]
- Tobalske, B.W. Aerodynamics of Avian Flight. Curr. Biol. 2022, 32, R1105–R1109. [Google Scholar] [CrossRef]
- Usherwood, J.R.; Hedrick, T.L.; Biewener, A.A. The aerodynamics of avian take-off from direct pressure measurements in Canada geese (Branta canadensis). J. Exp. Biol. 2003, 206, 4051–4066. [Google Scholar] [CrossRef]
- Green, S.I. Wing Tip Vortices. In Fluid Vortices; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1995; pp. 1–40. [Google Scholar]
- Voelkl, B.; Portugal, S.J.; Unsöld, M.; Usherwood, J.R.; Wilson, A.M.; Fritz, J. Matching Times of Leading and Following Suggest Cooperation through Direct Reciprocity during V-Formation Flight in Ibis. Proc. Natl. Acad. Sci. USA 2015, 112, 2115–2120. [Google Scholar] [CrossRef] [PubMed]
- Muijres, F.T.; Johansson, L.C.; Winter, Y.; Hedenström, A. Comparative aerodynamic performance of flapping flight in two bat species using time-resolved wake visualization. J. R. Soc. Interface 2011, 8, 1418–1428. [Google Scholar] [CrossRef] [PubMed]
- Hubel, T.Y.; Hristov, N.I.; Swartz, S.M.; Breuer, K.S. Changes in kinematics and aerodynamics over a range of speeds in Tadarida brasiliensis, the Brazilian free-tailed bat. J. R. Soc. Interface 2012, 9, 1120–1130. [Google Scholar] [CrossRef] [PubMed]
- Hedenström, A.; Muijres, F.; von Busse, R.; Johansson, L.; Winter, Y.; Spedding, G. High-speed stereo DPIV measurement of wakes of two bat species flying freely in a wind tunnel. Exp. Fluids 2009, 46, 923–932. [Google Scholar] [CrossRef]
- Hubel, T.Y.; Riskin, D.K.; Swartz, S.M.; Breuer, K.S. Wake structure and wing kinematics: The flight of the Lesser Dog-faced Fruit Bat, Cynopterus brachyotis. J. Exp. Biol. 2010, 213, 3427–3440. [Google Scholar] [CrossRef]
- Thielicke, W.; Stamhuis, E. The influence of wing morphology on the three-dimensional flow patterns of a flapping wing at bird scale. J. Fluid Mech. 2015, 768, 240–260. [Google Scholar] [CrossRef]
- Portugal, S.J.; Hubel, T.Y.; Fritz, J.; Heese, S.; Trobe, D.; Voelkl, B.; Hailes, S.; Wilson, A.M.; Usherwood, J.R. Upwash exploitation and downwash avoidance by flap phasing in Ibis formation flight. Nature 2014, 505, 399–402. [Google Scholar] [CrossRef]




| Variable | Description | Value |
|---|---|---|
| Chord length (c) | Distance between the front and rear edges of the wing | 0.3 m |
| Wing size | Total length of one wing | 0.72 m |
| Flight speed () | Average airspeed during flight | 13.9 m/s |
| Wingspan | Distance from wingtip to wingtip | 1.66 m |
| Flapping amplitude (k) | Maximum vertical movement of the wingtip | 69 cm |
| Wingbeat frequency (f) | Number of wingbeats per second | 4 Hz |
| Wavelength (λ) | Distance covered in one wingbeat | 3.475 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beaumont, F.; Murer, S.; Bogard, F.; Polidori, G. Aerodynamics of Flight Formations in Birds: A Quest for Energy Efficiency. Birds 2025, 6, 15. https://doi.org/10.3390/birds6020015
Beaumont F, Murer S, Bogard F, Polidori G. Aerodynamics of Flight Formations in Birds: A Quest for Energy Efficiency. Birds. 2025; 6(2):15. https://doi.org/10.3390/birds6020015
Chicago/Turabian StyleBeaumont, Fabien, Sébastien Murer, Fabien Bogard, and Guillaume Polidori. 2025. "Aerodynamics of Flight Formations in Birds: A Quest for Energy Efficiency" Birds 6, no. 2: 15. https://doi.org/10.3390/birds6020015
APA StyleBeaumont, F., Murer, S., Bogard, F., & Polidori, G. (2025). Aerodynamics of Flight Formations in Birds: A Quest for Energy Efficiency. Birds, 6(2), 15. https://doi.org/10.3390/birds6020015






