Ultraviolet, Did the Cell See It from the Side or the Bottom? Assessment and Modeling of UV Effects on Cultured Cells Using the CL-1000 UV-Crosslinker
Abstract
1. Introduction
2. Materials and Methods
2.1. Cells and Cell Culture
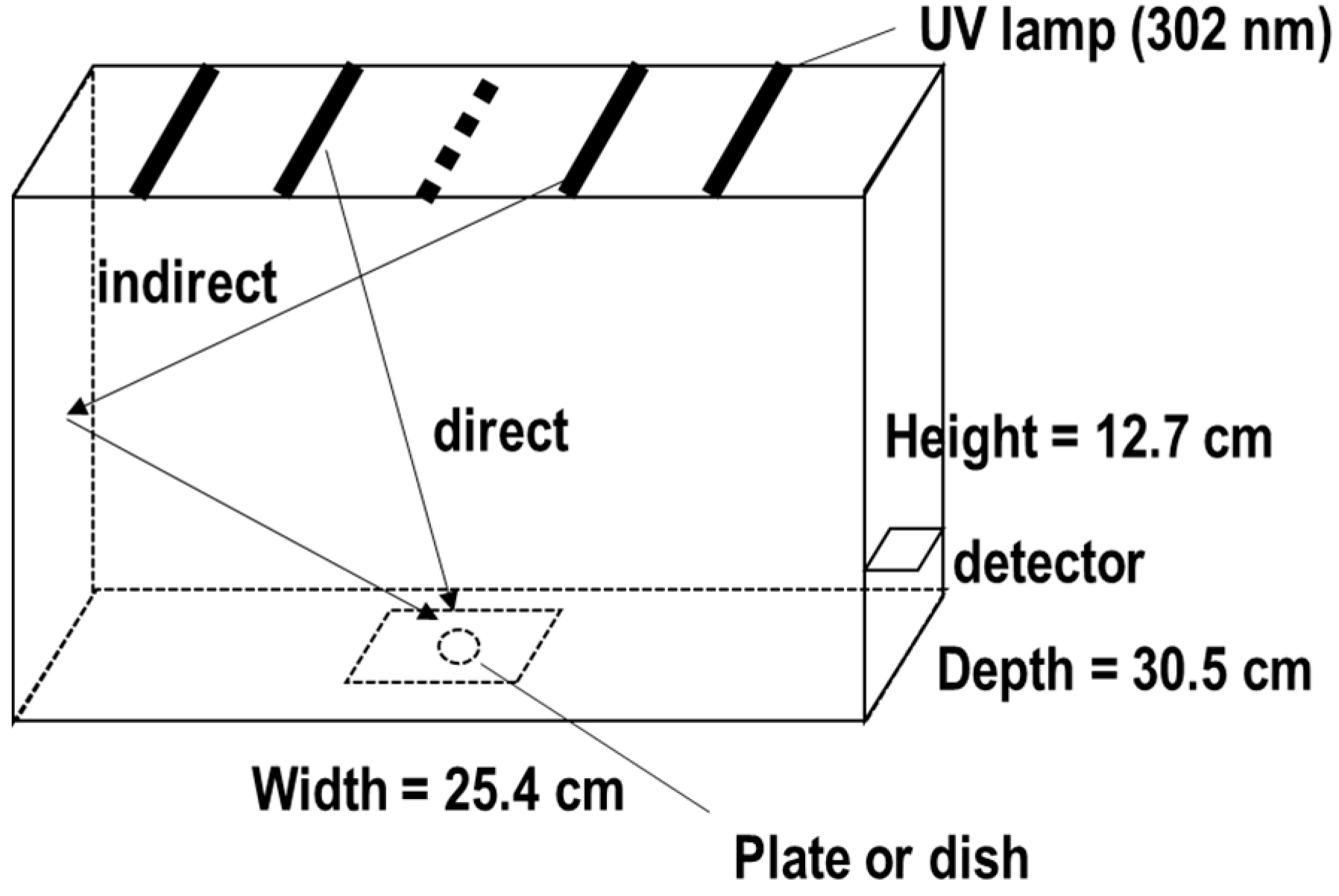
2.2. UV Exposure
2.3. Trypan Blue Dye Exclusion Assay
2.4. Hoechst 33342 Staining
2.5. WST-8 Assay
2.6. ELISA
2.7. Curve Fitting
2.8. Measurement of Transmittance (%T)
2.9. Statistical Analyses
2.10. Declarations of Generative AI in Scientific Writing
3. Results
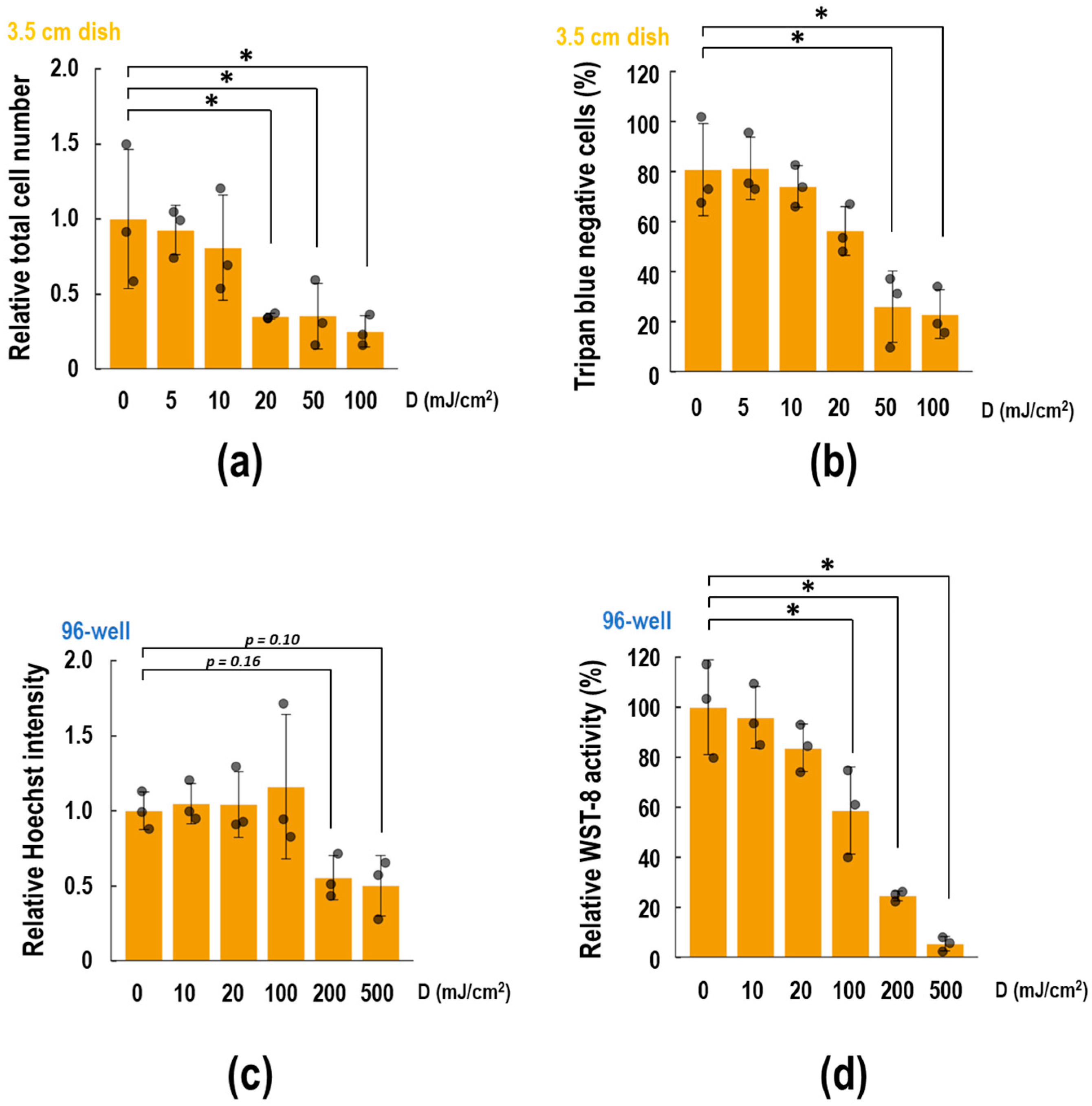
3.1. Analysis of Cytotoxic Effects Against UVB Exposure on Different Plate Formats
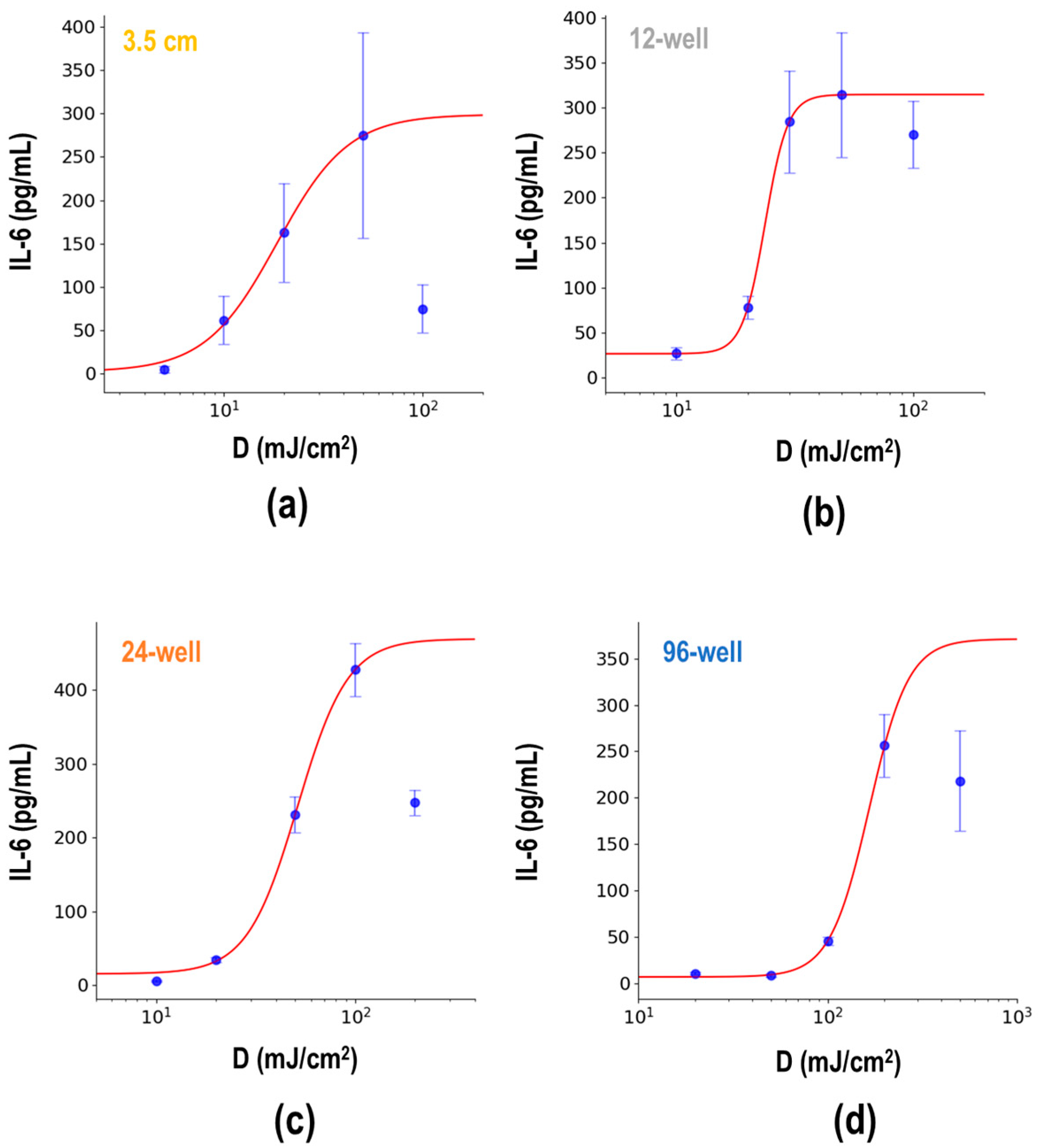
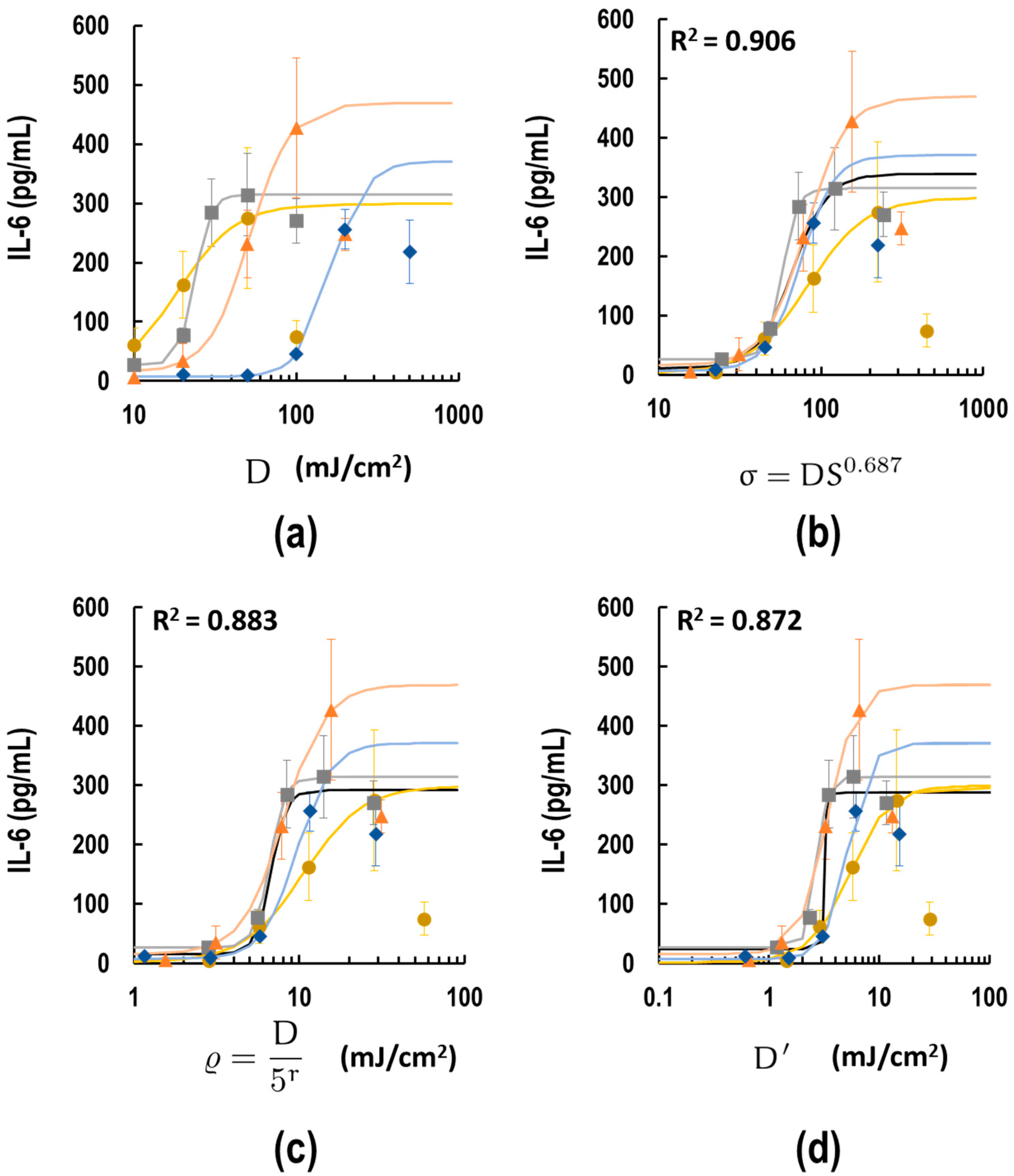
3.2. Analysis of IL-6 Release Against UVB Exposure across Different Plate Formats
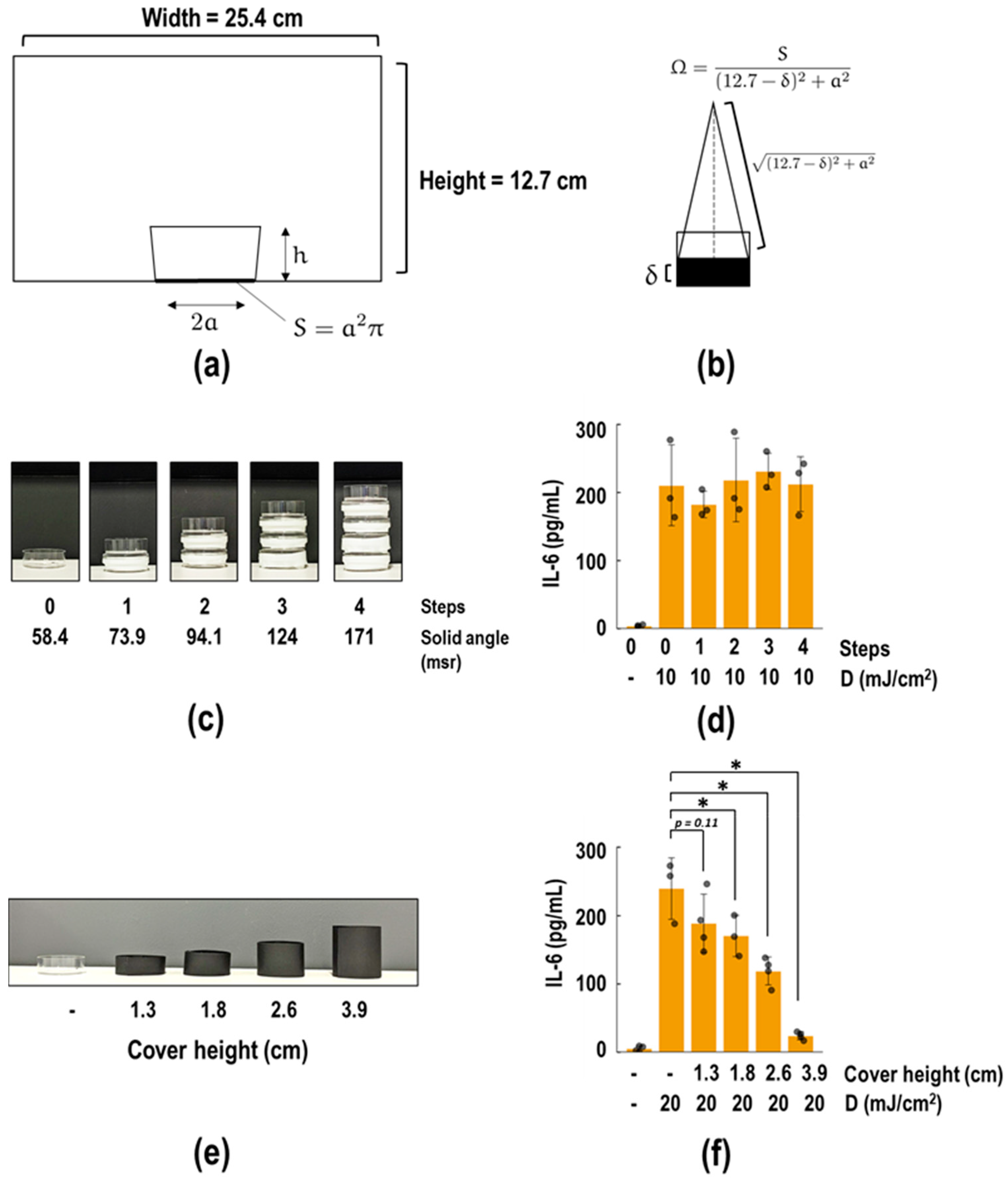
3.3. Effect of Equipment Configuration on the IL-6 Release
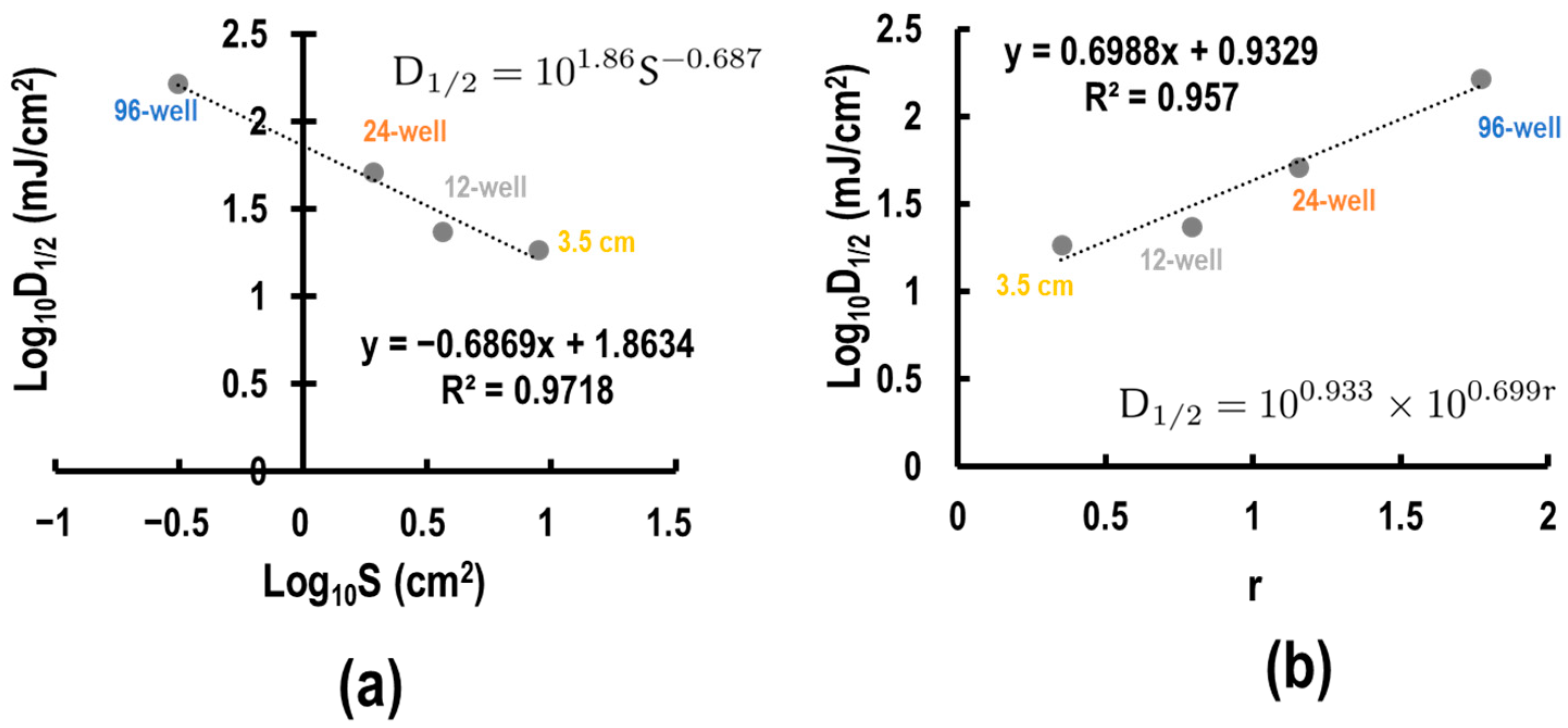
3.4. Development of Empirical Formula
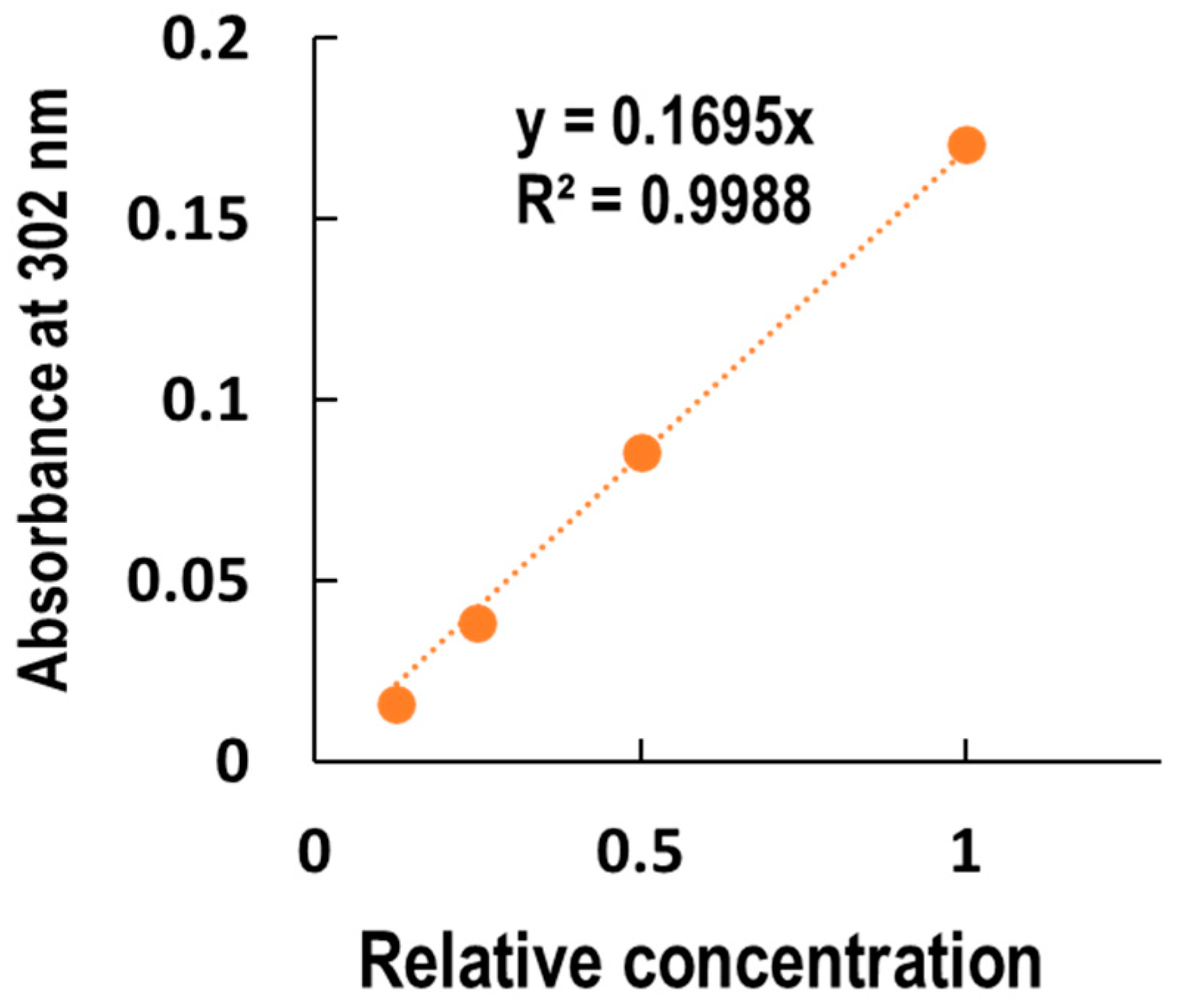
3.5. Calculation of the Absorptivity and Transmittance Rate
3.6. Comparison of the Adjustment of UV Dose by Indices σ, ρ and Model D′
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
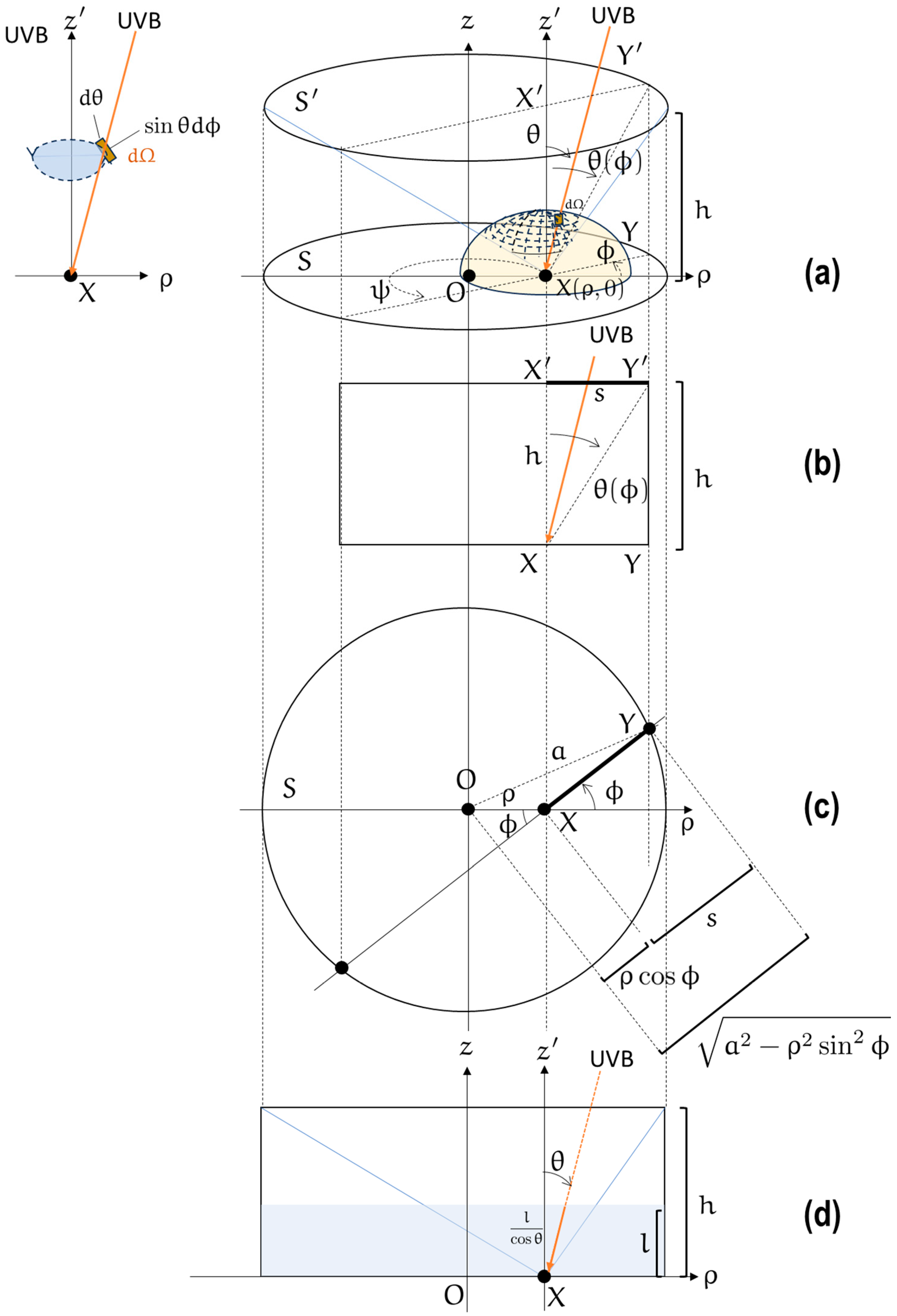
Appendix A. Model Development
References
- Matsumura, Y.; Ananthaswamy, H.N. Toxic Effects of Ultraviolet Radiation on the Skin. Toxicol. Appl. Pharmacol. 2004, 195, 298–308. [Google Scholar] [CrossRef] [PubMed]
- Berry, K.; Hallock, K.; Lam, C. Photoaging and Topical Rejuvenation. Clin. Plast. Surg. 2023, 50, 381–390. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Ke, J.; Wu, X.; Yan, Y. Astragaloside Prevents UV-Induced Keratinocyte Injury by Regulating TLR4/NF-κB Pathway. J. Cosmet. Dermatol. 2022, 21, 1163–1170. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Rybchyn, M.S.; De Silva, W.G.M.; Matthews, J.; Holland, A.J.A.; Conigrave, A.D.; Mason, R.S. UV-Induced DNA Damage in Skin Is Reduced by CaSR Inhibition. Photochem. Photobiol. 2022, 98, 1157–1166. [Google Scholar] [CrossRef]
- Takasawa, R.; Nakamura, H.; Mori, T.; Tanuma, S. Differential Apoptotic Pathways in Human Keratinocyte HaCaT Cells Exposed to UVB and UVC. Apoptosis 2005, 10, 1121–1130. [Google Scholar] [CrossRef]
- Watson, R.E.B.; Gibbs, N.K.; Griffiths, C.E.M.; Sherratt, M.J. Damage to Skin Extracellular Matrix Induced by UV Exposure. Antioxid. Redox Signal. 2014, 21, 1063–1077. [Google Scholar] [CrossRef]
- Ansary, T.M.; Hossain, M.R.; Kamiya, K.; Komine, M.; Ohtsuki, M. Inflammatory Molecules Associated with Ultraviolet Radiation-Mediated Skin Aging. Int. J. Mol. Sci. 2021, 22, 3974. [Google Scholar] [CrossRef]
- Salminen, A.; Kaarniranta, K.; Kauppinen, A. Photoaging: UV Radiation-Induced Inflammation and Immunosuppression Accelerate the Aging Process in the Skin. Inflamm. Res. 2022, 71, 817–831. [Google Scholar] [CrossRef]
- Fernandes, A.; Rodrigues, P.M.; Pintado, M.; Tavaria, F.K. A Systematic Review of Natural Products for Skin Applications: Targeting Inflammation, Wound Healing, and Photo-Aging. Phytomedicine 2023, 115, 154824. [Google Scholar] [CrossRef]
- Saewan, N.; Jimtaisong, A. Natural Products as Photoprotection. J. Cosmet. Dermatol. 2015, 14, 47–63. [Google Scholar] [CrossRef]
- He, H.; Li, A.; Li, S.; Tang, J.; Li, L.; Xiong, L. Natural Components in Sunscreens: Topical Formulations with Sun Protection Factor (SPF). Biomed. Pharmacother. 2021, 134, 111161. [Google Scholar] [CrossRef] [PubMed]
- Silva, M.R.F.; Alves, M.F.R.P.; Cunha, J.P.G.Q.; Costa, J.L.; Silva, C.A.; Fernandes, M.H.V.; Vilarinho, P.M.; Ferreira, P. Nanostructured Transparent Solutions for UV-Shielding: Recent Developments and Future Challenges. Mater. Today Phys. 2023, 35, 101131. [Google Scholar] [CrossRef]
- Kowalski, W. Mathematical Modeling of UV Disinfection. In Ultraviolet Germicidal Irradiation Handbook; Springer: Berlin/Heidelberg, Germany, 2009; pp. 51–72. ISBN 978-3-642-01998-2. [Google Scholar]
- Luangpraditkun, K.; Charoensit, P.; Grandmottet, F.; Viennet, C.; Viyoch, J. Photoprotective Potential of the Natural Artocarpin against In Vitro UVB-Induced Apoptosis. Oxidative Med. Cell. Longev. 2020, 2020, 1042451. [Google Scholar] [CrossRef] [PubMed]
- Song, J.H.; Piao, M.J.; Han, X.; Kang, K.A.; Kang, H.K.; Yoon, W.J.; Ko, M.H.; Lee, N.H.; Lee, M.Y.; Chae, S.; et al. Anti-Wrinkle Effects of Sargassum Muticum Ethyl Acetate Fraction on Ultraviolet B-Irradiated Hairless Mouse Skin and Mechanistic Evaluation in the Human HaCaT Keratinocyte Cell Line. Mol. Med. Rep. 2016, 14, 2937–2944. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Kim, K.C.; Kim, D.; Kim, S.C.; Jung, E.; Park, D.; Hyun, J.W. Empetrum Nigrum Var. Japonicum Extract Suppresses Ultraviolet B-Induced Cell Damage via Absorption of Radiation and Inhibition of Oxidative Stress. Evid. -Based Complement. Altern. Med. 2013, 2013, 983609. [Google Scholar] [CrossRef]
- Lin, S.M.; Baek, C.Y.; Jung, J.-H.; Kim, W.S.; Song, H.-Y.; Lee, J.H.; Ji, H.J.; Zhi, Y.; Kang, B.S.; Bahn, Y.-S.; et al. Antioxidant Activities of an Exopolysaccharide (DeinoPol) Produced by the Extreme Radiation-Resistant Bacterium Deinococcus Radiodurans. Sci. Rep. 2020, 10, 55. [Google Scholar] [CrossRef]
- Ohnishi, T.; Hisadome, M.; Joji, K.; Chiba, N.; Amir, M.S.; Kanekura, T.; Matsuguchi, T. Ultraviolet B Irradiation Decreases CXCL10 Expression in Keratinocytes through Endoplasmic Reticulum Stress. J. Cell Biochem. 2021. [Google Scholar] [CrossRef]
- Xuan, S.H.; Park, Y.M.; Ha, J.H.; Jeong, Y.J.; Park, S.N. The Effect of Dehydroglyasperin C on UVB–Mediated MMPs Expression in Human HaCaT Cells. Pharmacol. Rep. 2017, 69, 1224–1231. [Google Scholar] [CrossRef]
- Chiang, H.-M.; Chen, H.-C.; Chiu, H.-H.; Chen, C.-W.; Wang, S.-M.; Wen, K.-C. Neonauclea Reticulata (Havil.) Merr Stimulates Skin Regeneration after UVB Exposure via ROS Scavenging and Modulation of the MAPK/MMPs/Collagen Pathway. Evid. -Based Complement. Altern. Med. 2013, 2013, 324864. [Google Scholar] [CrossRef]
- Jaisin, Y.; Ratanachamnong, P.; Wongsawatkul, O.; Watthammawut, A.; Malaniyom, K.; Natewong, S. Antioxidant and Anti-Inflammatory Effects of Piperine on UV-B-Irradiated Human HaCaT Keratinocyte Cells. Life Sci. 2020, 263, 118607. [Google Scholar] [CrossRef]
- Sebaugh, J.L. Guidelines for Accurate EC50/IC50 Estimation. Pharm. Stat. 2011, 10, 128–134. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Wang, Y. Growth Models in Aquaculture for Hybrid and Natural Groupers Based on Early Development Stage. Aquaculture 2024, 578, 740026. [Google Scholar] [CrossRef]
- Ruijter, J.M.; Thygesen, H.H.; Schoneveld, O.J.L.M.; Das, A.T.; Berkhout, B.; Lamers, W.H. Factor Correction as a Tool to Eliminate between-Session Variation in Replicate Experiments: Application to Molecular Biology and Retrovirology. Retrovirology 2006, 3, 2. [Google Scholar] [CrossRef] [PubMed]
- Ruijter, J.M.; Ruiz Villalba, A.; Hellemans, J.; Untergasser, A.; van den Hoff, M.J.B. Removal of between-Run Variation in a Multi-Plate qPCR Experiment. Biomol. Detect. Quantif. 2015, 5, 10–14. [Google Scholar] [CrossRef] [PubMed]
- Mansuri, R.; Diwan, A.; Kumar, H.; Dangwal, K.; Yadav, D. Potential of Natural Compounds as Sunscreen Agents. Pharmacogn. Rev. 2021, 15, 47. [Google Scholar] [CrossRef]
- Berridge, M.V.; Herst, P.M.; Tan, A.S. Tetrazolium Dyes as Tools in Cell Biology: New Insights into Their Cellular Reduction. Biotechnol. Annu. Rev. 2005, 11, 127–152. [Google Scholar] [CrossRef]
- Hu, X.-M.; Li, Z.-X.; Lin, R.-H.; Shan, J.-Q.; Yu, Q.-W.; Wang, R.-X.; Liao, L.-S.; Yan, W.-T.; Wang, Z.; Shang, L.; et al. Guidelines for Regulated Cell Death Assays: A Systematic Summary, A Categorical Comparison, A Prospective. Front. Cell Dev. Biol. 2021, 9, 634690. [Google Scholar] [CrossRef]
- Stepanenko, A.A.; Dmitrenko, V.V. Pitfalls of the MTT Assay: Direct and off-Target Effects of Inhibitors Can Result in over/Underestimation of Cell Viability. Gene 2015, 574, 193–203. [Google Scholar] [CrossRef]
- Aslantürk, Ö.S. In Vitro Cytotoxicity and Cell Viability Assays: Principles, Advantages, and Disadvantages. In Genotoxicity—A Predictable Risk to Our Actual. World; IntechOpen: London, UK, 2017; ISBN 978-1-78923-419-0. [Google Scholar]
| Cells | UV Dose (mJ/cm2) | Biological Events | Culture Plate | Author | Ref. |
|---|---|---|---|---|---|
| HaCaT | 150 | 44% of cell viability | 24-well | Kim et al. | [16] |
| NHEK | 120 | Intracellular ROS generation | 96-well plate | Lin et al. | [17] |
| NHEK/ HaCaT | <100 | Confirmation of not showing decrease in cell viability | 96-well plate | Ohnishi et al. | [18] |
| HaCaT | 80 | No effect on cell survival | 6 cm dish | Xuan et al. | [19] |
| MMP-1 expression | |||||
| NHEK/ HaCaT | 50 | Reduction in CXCL10 expression | N. D. 1 | Ohnishi et al. | [18] |
| Hs68 | 40 | MMP-1 expression | 10 cm dish | Chiang et al. | [20] |
| HaCaT | 30 | MMP-1 expression | N. D. 1 | Song et al. | [15] |
| 96-Well | 24-Well | 12-Well | 3.5 cm | |
|---|---|---|---|---|
| Supplier | BM Bio | Falcon | Sumitomo Bakelite Co., Ltd. | Sumitomo Bakelite Co., Ltd. |
| Catalog No. | 215,006 | 353,047 | MS-80120 | MS-10530 |
| Well diameter 2a (cm) | 0.63 | 1.557 | 2.15 | 3.36 |
| Surface area S = πa2 (cm2) | 0.31 | 1.90 | 3.63 | 8.87 |
| Well height h (cm) | 1.115 | 1.798 | 1.700 | 1.180 |
| r = h/2a | 1.770 | 1.155 | 0.791 | 0.351 |
| Number of cells N0 (cells/well) | 0.25 × 104 | 1.25 × 104 | 2.5 × 104 | 5.0 × 104 |
| Initial cell density N0/S (cells/cm2) | 8.0 × 104 | 6.6 × 104 | 6.9 × 104 | 5.6 × 104 |
| Culture medium v (mL) | 0.1 | 0.5 | 1.0 | 2.0 |
| Medium height l = v/S (cm) | 0.321 | 0.263 | 0.275 | 0.226 |
| Container | a | b | c (D1/2) | d | R2 |
|---|---|---|---|---|---|
| 3.5 cm dish | 2.0 | 2.4 | 18.5 | 298.9 | 0.997 |
| 12-well plate | 26.5 | 9.1 | 23.7 | 314.6 | 1.000 |
| 24-well plate | 15.5 | 3.4 | 51.4 | 469.2 | 0.998 |
| 96-well plate | 7.3 | 4.2 | 166.2 | 370.9 | 0.999 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oyama, T.; Yanagihara, K.; Arai, A.; Kamiya, T.; Oyama, M.; Tanikawa, T.; Abe, T.; Hatanaka, T. Ultraviolet, Did the Cell See It from the Side or the Bottom? Assessment and Modeling of UV Effects on Cultured Cells Using the CL-1000 UV-Crosslinker. BioTech 2024, 13, 44. https://doi.org/10.3390/biotech13040044
Oyama T, Yanagihara K, Arai A, Kamiya T, Oyama M, Tanikawa T, Abe T, Hatanaka T. Ultraviolet, Did the Cell See It from the Side or the Bottom? Assessment and Modeling of UV Effects on Cultured Cells Using the CL-1000 UV-Crosslinker. BioTech. 2024; 13(4):44. https://doi.org/10.3390/biotech13040044
Chicago/Turabian StyleOyama, Takahiro, Kai Yanagihara, Anna Arai, Takanori Kamiya, Midori Oyama, Takashi Tanikawa, Takehiko Abe, and Tomomi Hatanaka. 2024. "Ultraviolet, Did the Cell See It from the Side or the Bottom? Assessment and Modeling of UV Effects on Cultured Cells Using the CL-1000 UV-Crosslinker" BioTech 13, no. 4: 44. https://doi.org/10.3390/biotech13040044
APA StyleOyama, T., Yanagihara, K., Arai, A., Kamiya, T., Oyama, M., Tanikawa, T., Abe, T., & Hatanaka, T. (2024). Ultraviolet, Did the Cell See It from the Side or the Bottom? Assessment and Modeling of UV Effects on Cultured Cells Using the CL-1000 UV-Crosslinker. BioTech, 13(4), 44. https://doi.org/10.3390/biotech13040044








