Influence of Implant-Abutment Contact Surfaces and Prosthetic Screw Tightening on the Stress Concentration, Fatigue Life and Microgap Formation: A Finite Element Analysis
Abstract
:1. Introduction
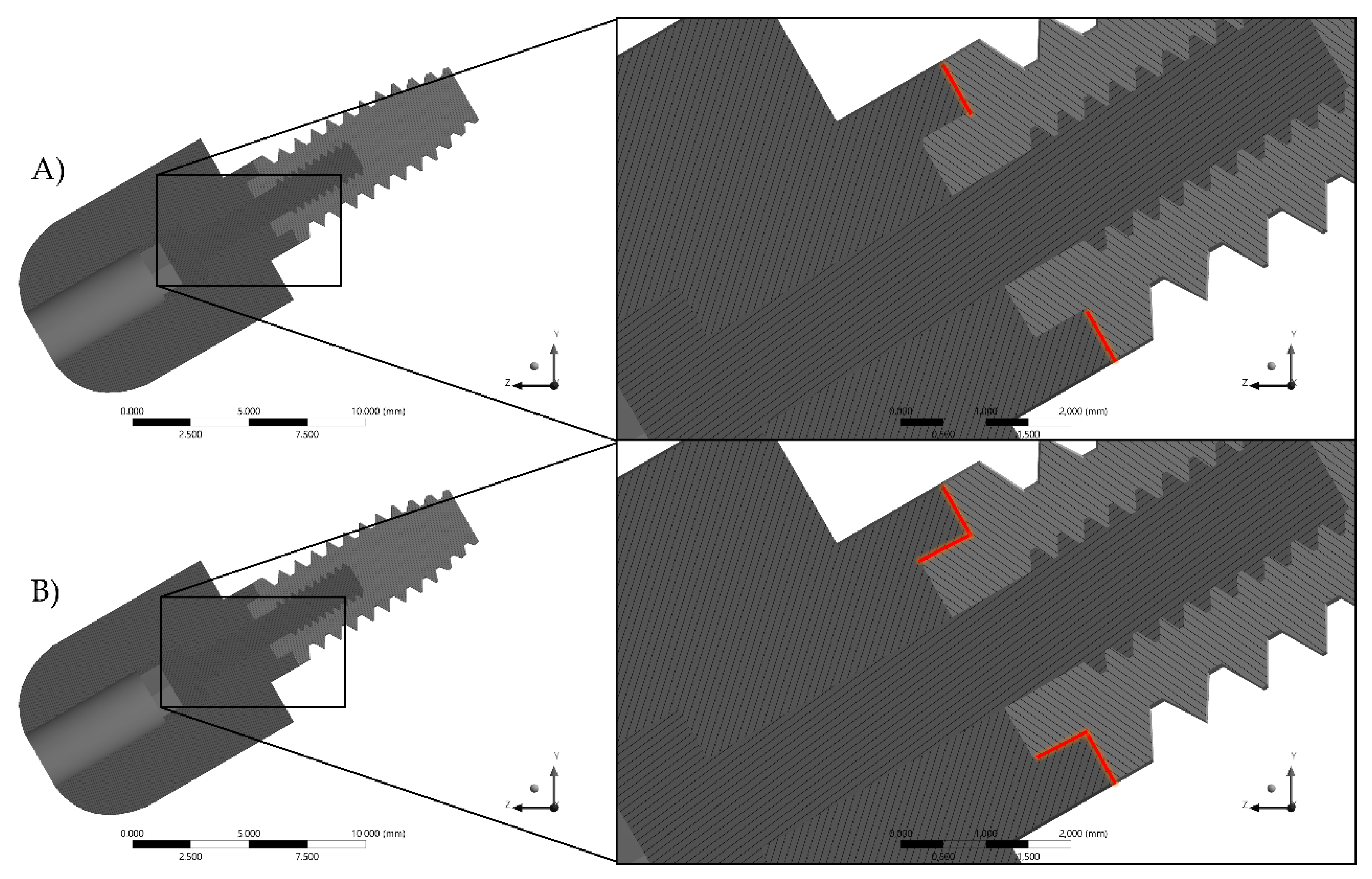
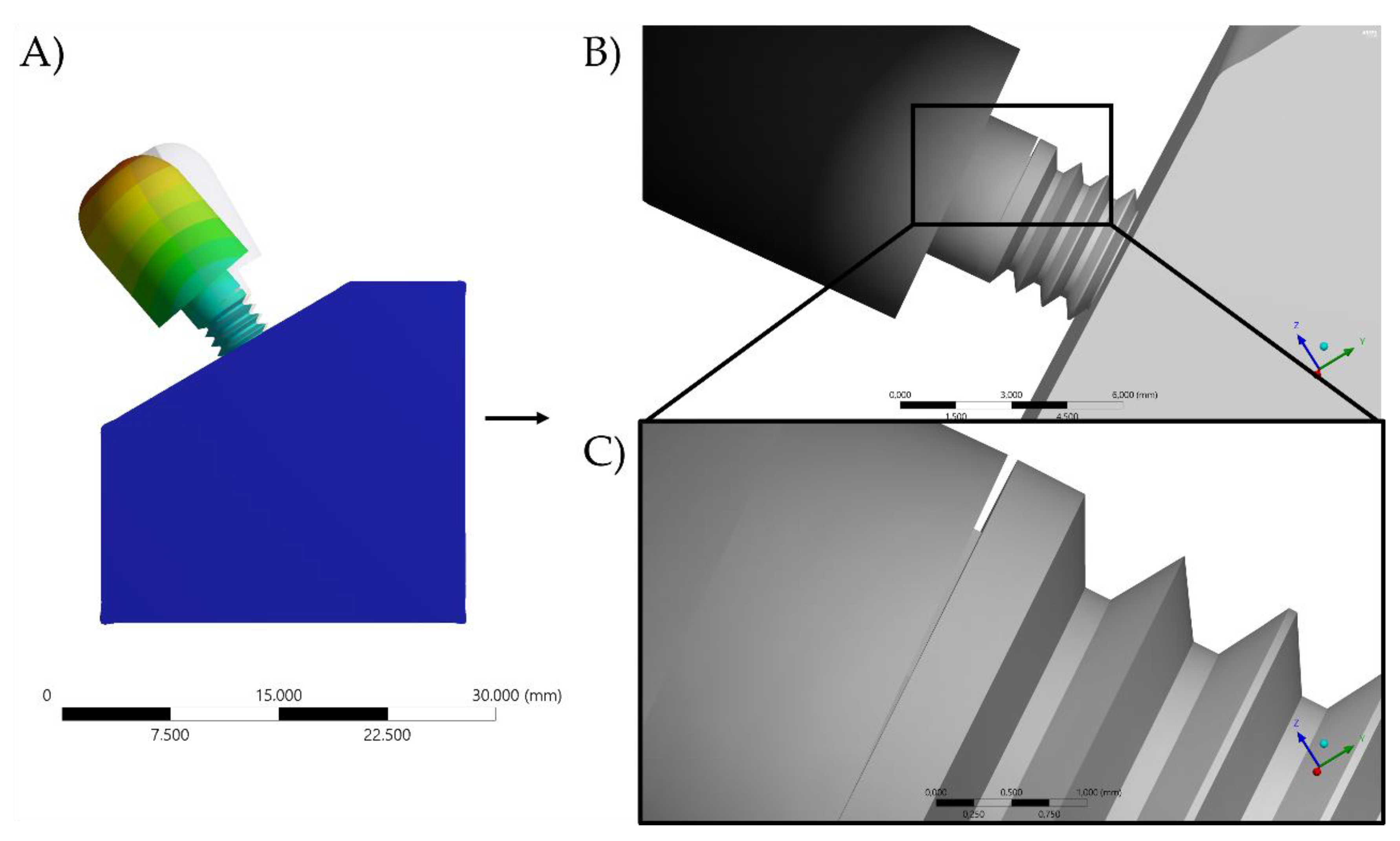
2. Materials and Methods
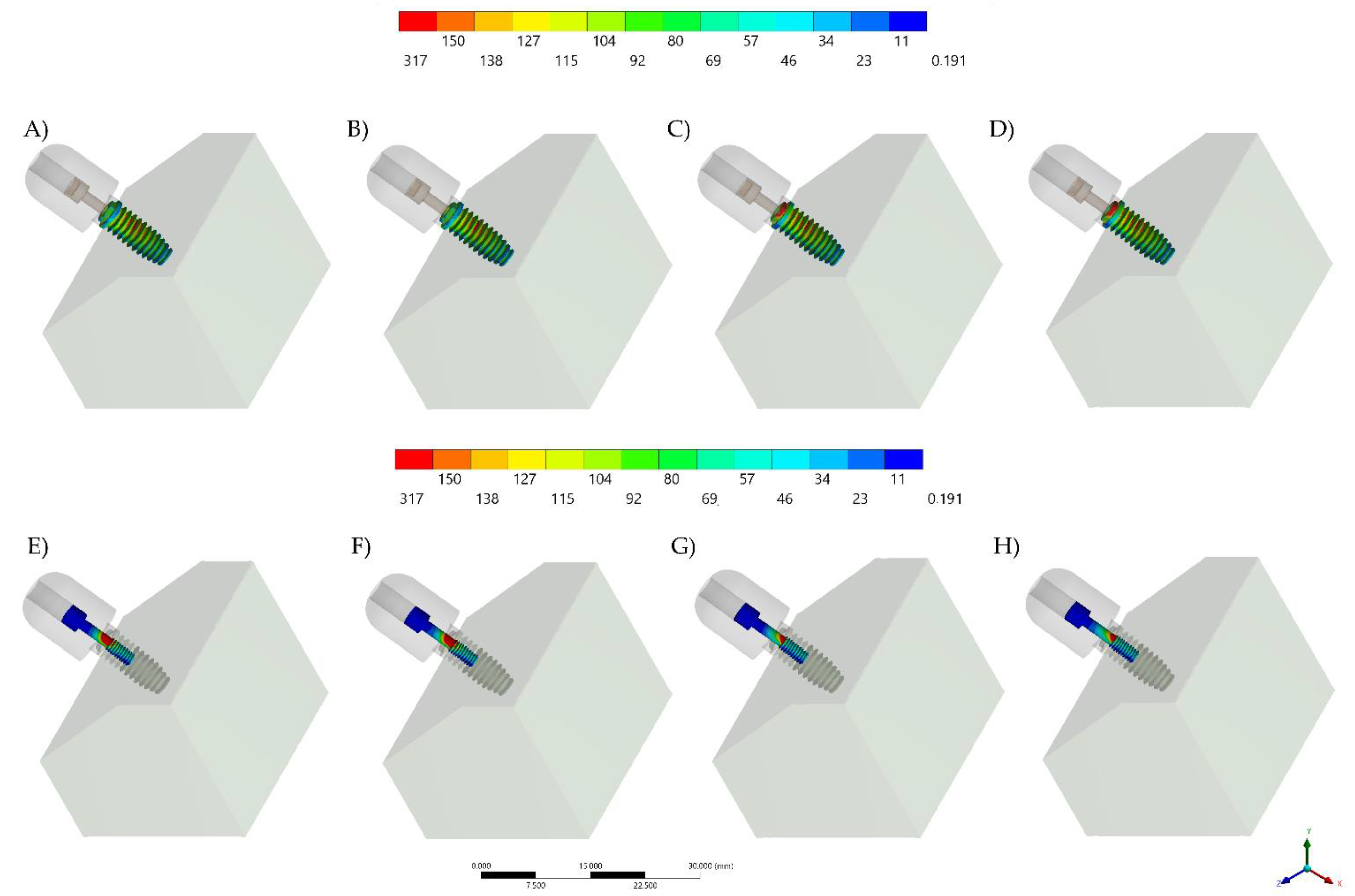
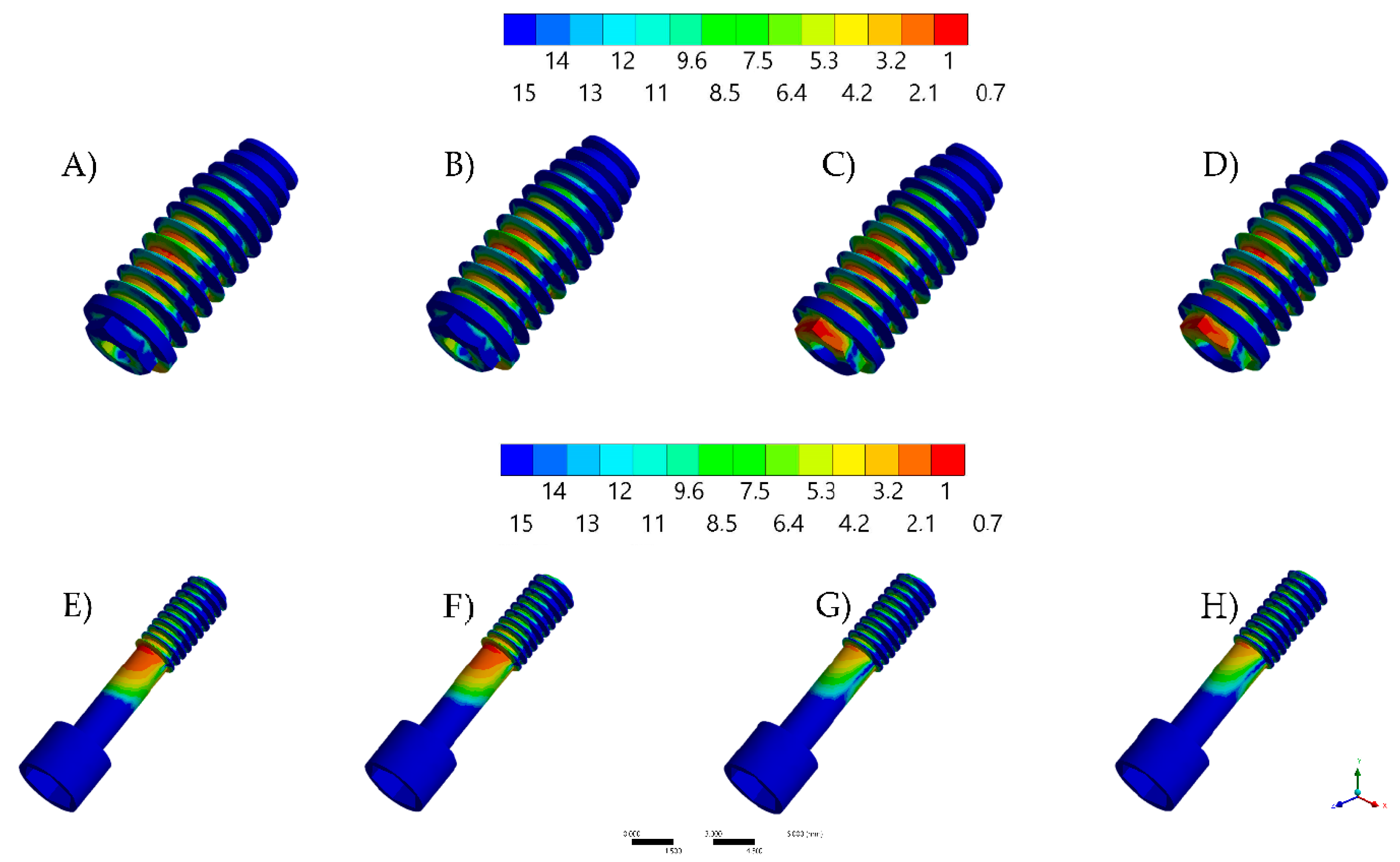
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tricio, J.; Laohapand, P.; van Steenberghe, D.; Quirynen, M.; Naert, I. Mechanical state assessment of the implant-bone continuum: A better understanding of the Periotest method. Int. J. Oral Maxillofac. Implant. 1995, 10, 43–49. [Google Scholar]
- Lauritano, D.; Moreo, G.; Lucchese, A.; Viganoni, C.; Limongelli, L.; Carinci, F. The Impact of Implant–Abutment Connection on Clinical Outcomes and Microbial Colonization: A Narrative Review. Materials 2020, 13, 1131. [Google Scholar] [CrossRef] [Green Version]
- Roccuzzo, A.; Stähli, A.; Monje, A.; Sculean, A.; Salvi, G.E. Peri-Implantitis: A Clinical Update on Prevalence and Surgical Treatment Outcomes. J. Clin. Med. 2021, 10, 1107. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Fok, A.; Aparicio, C.; Teng, W. Contact analysis of gap formation at dental implant-abutment interface under oblique loading: A numerical-experimental study. Clin. Implant Dent. Relat. Res. 2019, 21, 741–752. [Google Scholar] [CrossRef]
- Bassi, M.A.; Lopez, M.A.; Confalone, L.; Gaudio, R.M.; Lombardo, L.; Lauritano, D. A prospective evaluation of outcomes of two tapered implant systems. J. Biol. Regul. Homeost. Agents 2016, 30, 1–6. [Google Scholar]
- Scarano, A.; Valbonetti, L.; Degidi, M.; Pecci, R.; Piattelli, A.; de Oliveira, P.S.; Perrotti, V. Implant-Abutment Contact Surfaces and Microgap Measurements of Different Implant Connections Under 3-Dimensional X-Ray Microtomography. Implant. Dent. 2016, 25, 656–662. [Google Scholar] [CrossRef]
- Kim, J.H.; Noh, G.; Hong, S.J.; Lee, H. Biomechanical stress and microgap analysis of bone-level and tissue-level implant abutment structure according to the five different directions of occlusal loads. J. Adv. Prosthodont. 2020, 12, 316–321. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.-S.; Lim, Y.-J. Axial Displacements and Removal Torque Changes of Five Different Implant-Abutment Connections under Static Vertical Loading. Materials 2020, 13, 699. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tribst, J.P.M.; Dal Piva, A.M.D.O.; Lo Giudice, R.; Borges, A.L.S.; Bottino, M.A.; Epifania, E.; Ausiello, P. The Influence of Custom-Milled Framework Design for an Implant-Supported Full-Arch Fixed Dental Prosthesis: 3D-FEA Study. Int. J. Environ. Res. Public Health 2020, 17, 4040. [Google Scholar] [CrossRef] [PubMed]
- Vinhas, A.S.; Aroso, C.; Salazar, F.; López-Jarana, P.; Ríos-Santos, J.V.; Herrero-Climent, M. Review of the Mechanical Behavior of Different Implant–Abutment Connections. Int. J. Environ. Res. Public Health 2020, 17, 8685. [Google Scholar] [CrossRef]
- Bisognin, E.D.C.; Harari, N.D.; Machado, S.J.; da Silva, C.P.; de Almeida Soares, G.D.; Vidigal, G.M., Jr. Evaluation of implant-abutment microgap and bacterial leakage in five external-hex implant systems: An in vitro study. Int. J. Oral Maxillofac. Implant. 2012, 27, 346–351. [Google Scholar]
- Gigandet, M.; Bigolin, G.; Faoro, F.; Bürgin, W.; Brägger, U. Implants with original and non-original abutment connections. Clin. Implant Dent. Relat. Res. 2014, 16, 303–311. [Google Scholar] [CrossRef] [PubMed]
- Fernández-Asián, I.; Martínez-González, Á.; Torres-Lagares, D.; Serrera-Figallo, M.-Á.; Gutiérrez-Pérez, J.-L. External Connection versus Internal Connection in Dental Implantology. A Mechanical in vitro Study. Metals 2019, 9, 1106. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.; Jo, M.; Noh, G. Biomechanical effects of dental implant diameter, connection type, and bone density on microgap formation and fatigue failure: A finite element analysis. Comput. Methods Programs Biomed. 2021, 200, 105863. [Google Scholar] [CrossRef]
- Tonin, B.S.H.; He, Y.; Ye, N.; Chew, H.P.; Fok, A. Effects of tightening torque on screw stress and formation of implant-abutment microgaps: A finite element analysis. J. Prosthet. Dent. 2021, 17, S0022–S3913. [Google Scholar]
- Wiest, W.; Rack, A.; Zabler, S.; Schaer, A.; Swain, M.; Nelson, K. Validation of finite-element simulations with synchrotron radiography—A descriptive study of micromechanics in two-piece dental implants. Heliyon 2018, 4, e00524. [Google Scholar] [CrossRef] [Green Version]
- Shemtov-Yona, K.; Rittel, D. Fatigue of Dental Implants: Facts and Fallacies. Dent. J. 2016, 4, 16. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Prados-Privado, M.; Ivorra, C.; Martínez-Martínez, C.; Gehrke, S.A.; Calvo-Guirado, J.L.; Prados-Frutos, J.C. A Finite Element Analysis of the Fatigue Behavior and Risk of Failure of Immediate Provisional Implants. Metals 2019, 9, 535. [Google Scholar] [CrossRef] [Green Version]
- Armentia, M.; Abasolo, M.; Coria, I.; Albizuri, J. Fatigue Design of Dental Implant Assemblies: A Nominal Stress Approach. Metals 2020, 10, 744. [Google Scholar] [CrossRef]
- UNE-EN ISO 14801:2016. Dentistry—Implants—Dynamic Loading Test for Endosseous Dental Implants; International Organozation for Standardization: Geneva, Switzerland, 2017. [Google Scholar]
- Tribst, J.P.M.; Piva, A.M.D.O.D.; Anami, L.C.; Borges, A.L.S.; Bottino, M. A Influence of implant connection on the stress distribution in restorations performed with hybrid abutments. J. Osseointegration 2019, 11, 507–512. [Google Scholar]
- Sahoo, P.; Das, S.K.; Davim, J.P. Tribology of materials for biomedical applications. Mech. Behav. Biomater. 2019, 1–45. [Google Scholar] [CrossRef]
- Osman, R.B.; Swain, M.V. A Critical Review of Dental Implant Materials with an Emphasis on Titanium versus Zirconia. Materials 2015, 8, 932–958. [Google Scholar] [CrossRef] [Green Version]
- Janeček, M.; Nový, F.; Harcuba, P.; Stráský, J.; Trško, L.; Mhaede, M.; Wagner, L. The Very High Cycle Fatigue Behavior of Ti-6Al-4V Alloy. Acta Phys. Pol. A 2015, 128, 497–502. [Google Scholar] [CrossRef]
- Jörn, D.; Kohorst, P.; Besdo, S.; Borchers, L.; Stiesch, M. Three-Dimensional Nonlinear Finite Element Analysis and Microcomputed Tomography Evaluation of Microgap Formation in a Dental Implant under Oblique Loading. Int. J. Oral Maxillofac. Implant. 2016, 31, 32–42. [Google Scholar] [CrossRef]
- Tsai, Y.T.; Wang, K.S.; Woo, J.C. Fatigue life and reliability evaluation for dental implants based on computer simulation and limited test data. J. Mech. Eng. Sci. 2013, 227, 554–564. [Google Scholar] [CrossRef]
- Prados-Privado, M.; Prados-Frutos, J.C.; Manchón, Á.; Rojo, R.; Felice, P.; Bea, J.A. Dental implants fatigue as a possible failure of implantologic treatment: The importance of randomness in fatigue behaviour. BioMed Res. Int. 2015, 2015, 825402. [Google Scholar] [CrossRef] [Green Version]
- Prabhudesai, A.; Dhatrak, P.N.; Padmanabhan, D. Fatigue Life Prediction of Dental Implants. Int. J. Eng. Technol. Comput. Res. 2017, 5, 153–160. [Google Scholar]
- Tribst, J.P.M.; Dal Piva, A.M.O.; Borges, A.L.S.; Anami, L.C.; Kleverlaan, C.J.; Bottino, M.A. Survival Probability, Weibull Characteristics, Stress Distribution, and Fractographic Analysis of Polymer-Infiltrated Ceramic Network Restorations Cemented on a Chairside Titanium Base: An In Vitro and In Silico Study. Materials 2020, 13, 1879. [Google Scholar] [CrossRef] [PubMed]
- García-González, M.; Blasón-González, S.; García-García, I.; Lamela-Rey, M.J.; Fernández-Canteli, A.; Álvarez-Arenal, Á. Optimized Planning and Evaluation of Dental Implant Fatigue Testing: A Specific Software Application. Biology 2020, 9, 372. [Google Scholar] [CrossRef] [PubMed]
- Tribst, J.P.M.; Dal Piva, A.M.D.O.; Borges, A.L.S.; Bottino, M.A. Different combinations of CAD/CAM materials on the biomechanical behavior of a two-piece prosthetic solution. Int. J. Comput. Dent. 2019, 22, 171–176. [Google Scholar] [PubMed]
- Tribst, J.P.M.; Dal Piva, A.M.O.; Shibli, J.A.; Borges, A.L.S.; Tango, R.N. Influence of implantoplasty on stress distribution of exposed implants at different bone insertion levels. Braz. Oral Res. 2017, 7, 96. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Datte, C.E.; Tribst, J.P.; Dal Piva, A.O.; Nishioka, R.S.; Bottino, M.A.; Evangelhista, A.M.; Monteiro, F.M.M.; Borges, A.L. Influence of different restorative materials on the stress distribution in dental implants. J. Clin. Exp. Dent. 2018, 10, 439–444. [Google Scholar] [CrossRef]
- Adolfi, D.; Mendes Tribst, J.P.; Souto Borges, A.L.; Bottino, M.A. Torque Maintenance Capacity, Vertical Misfit, Load to Failure, and Stress Concentration of Zirconia Restorations Cemented or Notched to Titanium Bases. Int. J. Oral Maxillofac. Implant. 2020, 35, 357–365. [Google Scholar] [CrossRef]
- Melo Filho, A.B.D.; Tribst, J.P.M.; Ramos, N.D.C.; Luz, J.N.; Jardini, M.A.N.; Borges, A.L.S.; Santamaria, M.P.; Melo, R.M.D. Failure probability, stress distribution and fracture analysis of experimental screw for micro conical abutment. Braz. Dent. J. 2019, 30, 157–163. [Google Scholar] [CrossRef] [Green Version]
- Torres-Alemany, A.; Fernández-Estevan, L.; Agustín-Panadero, R.; Montiel-Company, J.M.; Labaig-Rueda, C.; Mañes-Ferrer, J.F. Clinical Behavior of Short Dental Implants: Systematic Review and Meta-Analysis. J. Clin. Med. 2020, 9, 3271. [Google Scholar] [CrossRef]
- Ausiello, P.; Dal Piva, A.M.d.O.; Borges, A.L.S.; Lanzotti, A.; Zamparini, F.; Epifania, E.; Mendes Tribst, J.P. Effect of Shrinking and No Shrinking Dentine and Enamel Replacing Materials in Posterior Restoration: A 3D-FEA Study. Appl. Sci. 2021, 11, 2215. [Google Scholar] [CrossRef]
- Martorelli, M.; Ausiello, P. A novel approach for a complete 3D tooth reconstruction using only 3D crown data. Int. J. Interact. Des. Manuf. 2013, 7, 125–133. [Google Scholar] [CrossRef]
- Prati, C.; Tribst, J.P.M.; Dal Piva, A.M.d.O.; Borges, A.L.S.; Ventre, M.; Zamparini, F.; Ausiello, P. 3D Finite Element Analysis of Rotary Instruments in Root Canal Dentine with Different Elastic Moduli. Appl. Sci. 2021, 11, 2547. [Google Scholar] [CrossRef]





| Material | Elastic Modulus (GPa) | Poisson Ratio | Ultimate Tensile Strength (MPa) | Yield Strength (MPa) |
|---|---|---|---|---|
| Fixation base | 3.6 | 0.3 | - | - |
| Titanium | 110 | 0.3 | 930 | 860 |
| Torque of Screw | Contacting Surfaces | Stress (MPa) | |
|---|---|---|---|
| Implant | Screw | ||
| 20 Ncm | Axials and surrounding | 279 | 283 |
| Surrounding only | 256 | 374 | |
| 30 Ncm | Axials and surrounding | 268 | 287 |
| Surrounding only | 253 | 419 | |
| Torque of Screw | Contacting Surfaces | Safety Factor | |
|---|---|---|---|
| Implant | Screw | ||
| 20 Ncm | Axials and surrounding | 1.60 | 1.51 |
| Surrounding only | 1.49 | 0.76 | |
| 30 Ncm | Axials and surrounding | 1.61 | 1.44 |
| Surrounding only | 1.50 | 0.72 | |
| Torque of Screw | Contacting Surfaces | Life (Cycles) | |
|---|---|---|---|
| Implant | Screw | ||
| 20 Ncm | Axials and surrounding | 1 × 1010 | 1 × 1010 |
| Surrounding only | 1 × 1010 | 63,567 | |
| 30 Ncm | Axials and surrounding | 1 × 1010 | 1 × 1010 |
| Surrounding only | 1 × 1010 | 57,389 | |
| Torque of Screw | Contacting Surfaces | Microgap (mm) |
|---|---|---|
| Interface Implant-Abutment | ||
| 20 Ncm | Axials and surrounding | 0.000861 |
| Surrounding only | 0.001817 | |
| 30 Ncm | Axials and surrounding | 0.000820 |
| Surrounding only | 0.001751 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tribst, J.P.M.; Dal Piva, A.M.d.O.; da Silva-Concílio, L.R.; Ausiello, P.; Kalman, L. Influence of Implant-Abutment Contact Surfaces and Prosthetic Screw Tightening on the Stress Concentration, Fatigue Life and Microgap Formation: A Finite Element Analysis. Oral 2021, 1, 88-101. https://doi.org/10.3390/oral1020009
Tribst JPM, Dal Piva AMdO, da Silva-Concílio LR, Ausiello P, Kalman L. Influence of Implant-Abutment Contact Surfaces and Prosthetic Screw Tightening on the Stress Concentration, Fatigue Life and Microgap Formation: A Finite Element Analysis. Oral. 2021; 1(2):88-101. https://doi.org/10.3390/oral1020009
Chicago/Turabian StyleTribst, João Paulo Mendes, Amanda Maria de Oliveira Dal Piva, Laís Regiane da Silva-Concílio, Pietro Ausiello, and Les Kalman. 2021. "Influence of Implant-Abutment Contact Surfaces and Prosthetic Screw Tightening on the Stress Concentration, Fatigue Life and Microgap Formation: A Finite Element Analysis" Oral 1, no. 2: 88-101. https://doi.org/10.3390/oral1020009
APA StyleTribst, J. P. M., Dal Piva, A. M. d. O., da Silva-Concílio, L. R., Ausiello, P., & Kalman, L. (2021). Influence of Implant-Abutment Contact Surfaces and Prosthetic Screw Tightening on the Stress Concentration, Fatigue Life and Microgap Formation: A Finite Element Analysis. Oral, 1(2), 88-101. https://doi.org/10.3390/oral1020009








