Interpreting Bar Charts: Effects of 3D Depth Cues on Human Gaze and User Understanding
Abstract
1. Introduction
2. Materials and Methods
2.1. Online Survey Design (Experiment 1)
2.2. Eye Tracking Methodology (Experiment 2)
3. Results
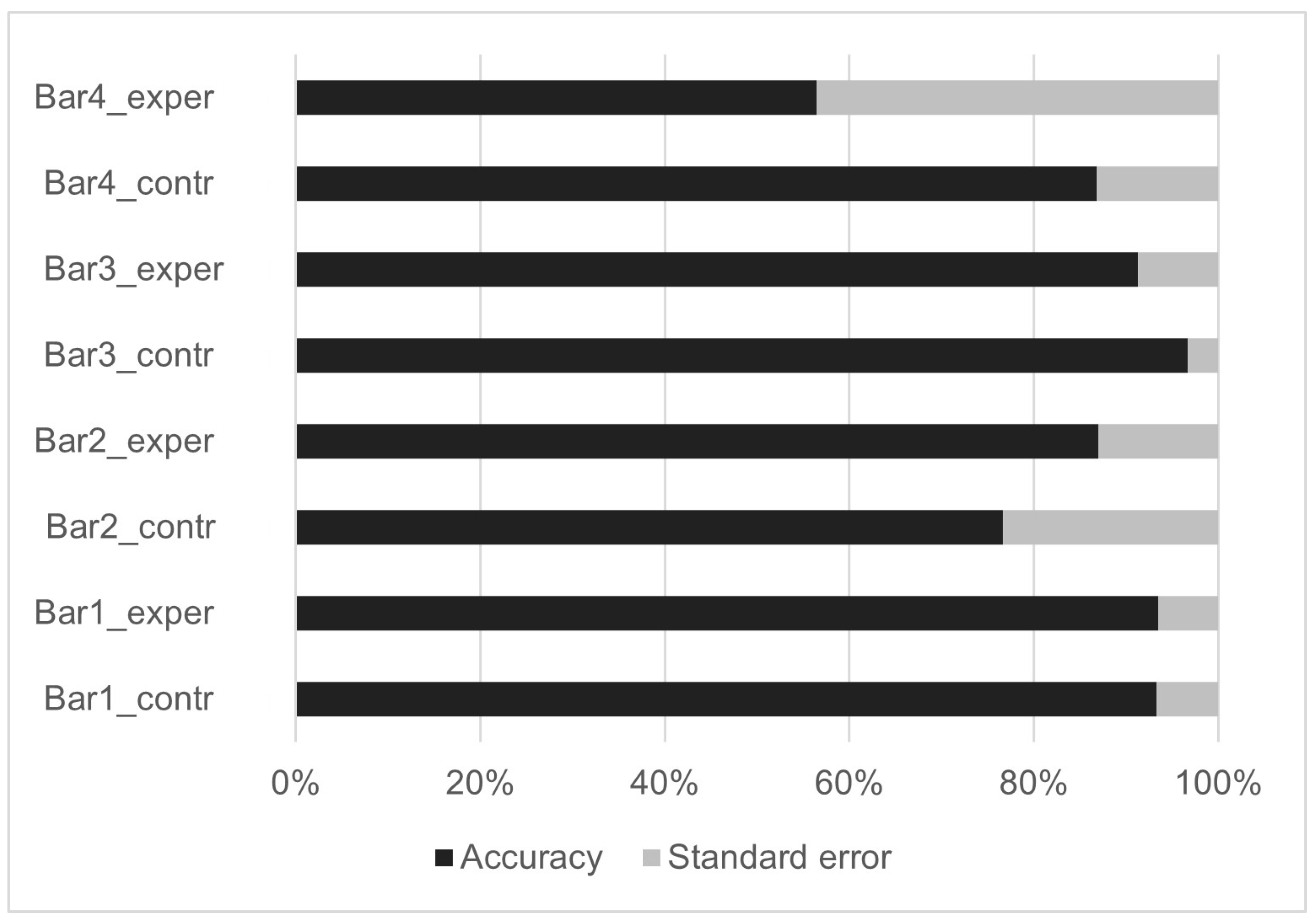
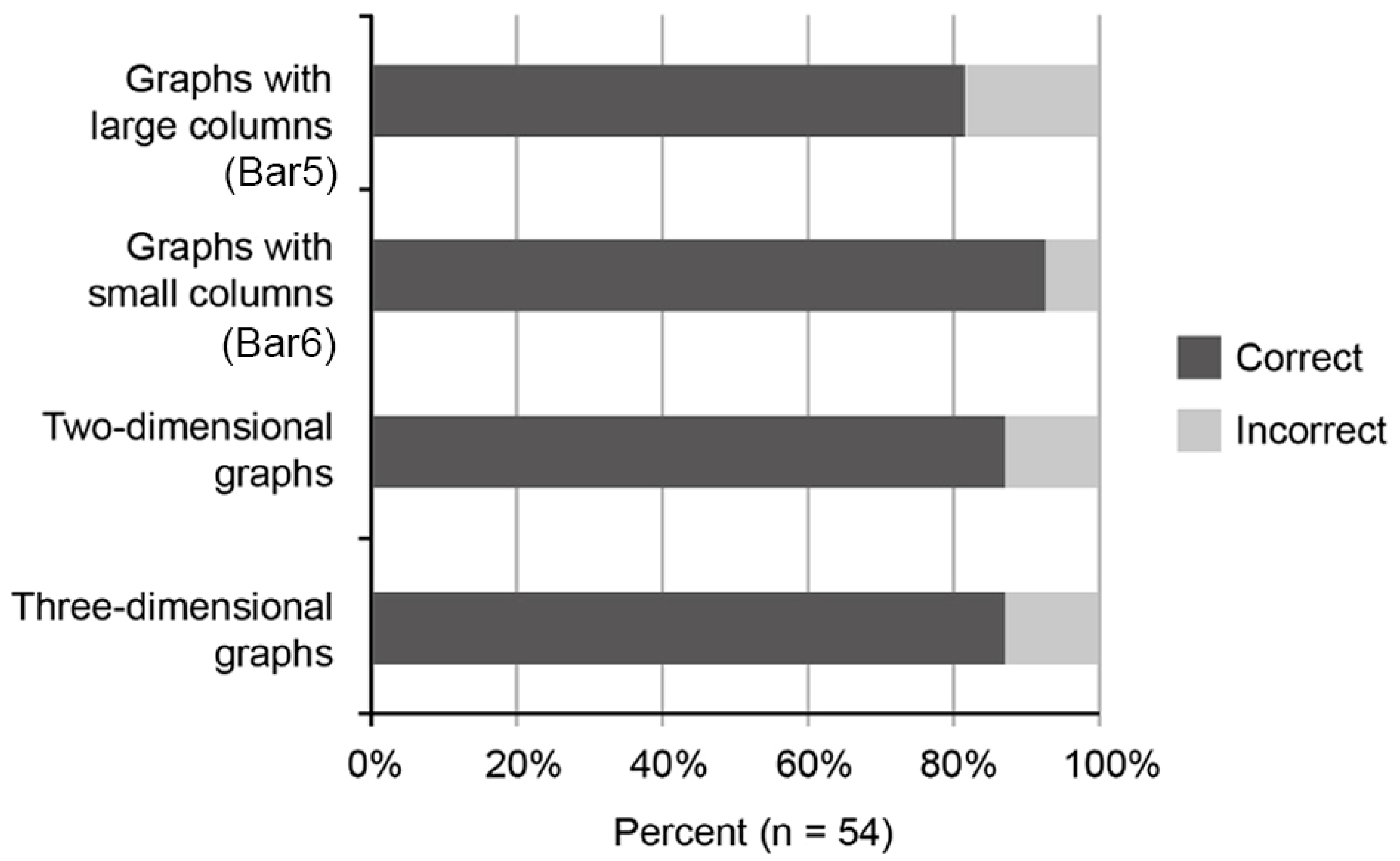
3.1. Results of the Online Survey (Experiment 1)
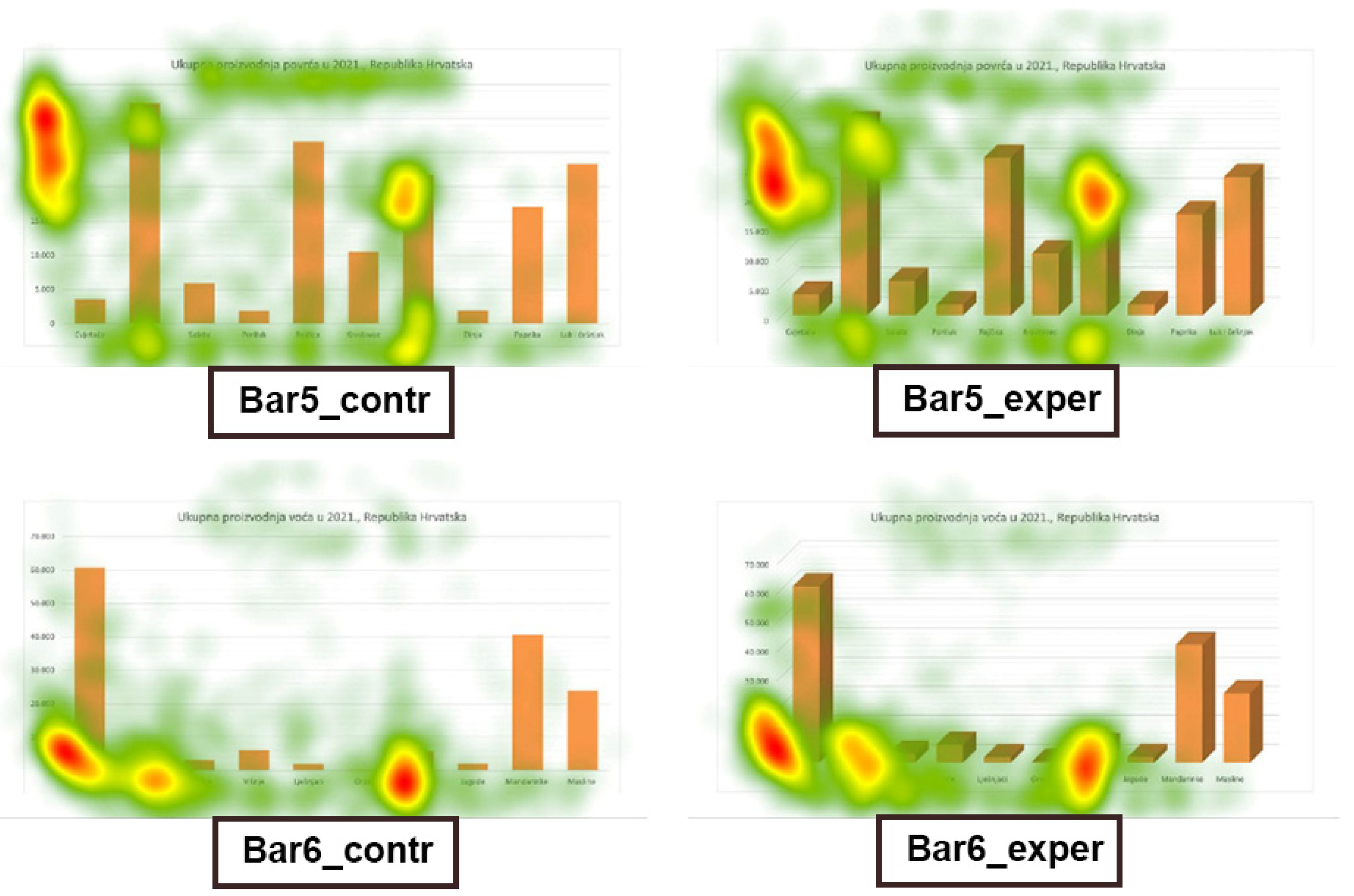
3.2. Results of the Eye Tracking (Experiment 2)
4. Discussion
- There is no association between the type of graph (2D or 3D) and the accuracy of responses for bar charts, refuting our first hypothesis (H1).
- Our results indicate that there is no difference in visual information processing between 2D and 3D bar charts that impacts the perception of the size relationships represented in the visualizations, refuting our second hypothesis (H2).
- While users expressed a preference for the 2D bar chart display when reading values, they demonstrated a high level of accuracy in interpreting values from the 3D bar chart displays as well.
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cairo, A. How Charts Lie; W. W. Norton & Company: New York, NY, USA, 2019. [Google Scholar]
- Szafir, D.A. The Good, the Bad, and the Biased: Five Ways Visualizations Can Mislead (and How to Fix Them). Interactions 2018, 25, 26–33. [Google Scholar] [CrossRef]
- Brath, R. 3D InfoVis is here to stay: Deal with it. In Proceedings of the 2014 IEEE VIS International Workshop on 3DVis (3DVis), Paris, France, 9 November 2014; pp. 25–31. [Google Scholar] [CrossRef]
- Brinton, W.C. Graphic Methods for Presenting Facts; The Engineering Magazine Company: Delhi, India, 1914. [Google Scholar]
- Cleveland, W.S.; McGill, R. An experiment in graphical perception. Int. J. Man-Mach. Stud. 1986, 25, 491–500. [Google Scholar] [CrossRef]
- McNabb, L.; Laramee, R.S. Survey of Surveys (SoS)—Mapping the Landscape of Survey Papers in Information Visualization. Comput. Graph. Forum 2017, 36, 589–617. [Google Scholar] [CrossRef]
- Juřík, V.; Herman, L.; Šašinka, Č.; Stachoň, Z.; Chmelík, J. When the display matters: A multifaceted perspective on 3D geovisualizations. Open Geosci. 2017, 1, 89–100. [Google Scholar] [CrossRef]
- Sieber, R.; Schnürer, R.; Eichenberger, R.; Hurni, L. The Power of 3D Real-Time Visualization in Atlases—Concepts, Techniques, and Implementation. In Proceedings of the International Cartographic Conference, Dresden, Germany, 25–30 August 2013. [Google Scholar]
- Watson, D.; Fitzmaurice, G.; Matejka, J. How Tall is that Bar Chart? Virtual Reality, Distance Compression and Visualizations. In Proceedings of the Graphics Interface, Virtual Event, 27–28 May 2021; pp. 256–264. [Google Scholar] [CrossRef]
- Seipel, S.; Carvalho, L. Solving Combined Geospatial Tasks Using 2D and 3D Bar Charts. In Proceedings of the 16th International Conference on Information Visualisation, Montpellier, France, 11–13 July 2012; pp. 157–163. [Google Scholar] [CrossRef]
- Bedjaoui, M.; Elouali, N.; Benslimane, S.M.; Şengel, E. Suggestion pattern on online social networks: Between intensity, effectiveness and user’s satisfaction. Vis. Comput. 2022, 38, 1331–1343. [Google Scholar] [CrossRef]
- Hughes, B.M. Just noticeable differences in 2D and 3D bar charts: A psychophysical analysis of chart readability. Percept. Mot. Ski. 2001, 92, 495–503. [Google Scholar] [CrossRef] [PubMed]
- Burch, M. The Aesthetics of Diagrams. In Proceedings of the 6th International Conference on Information Visualization Theory and Applications (VISIGRAPP 2015)—IVAPP, Berlin, Germany, 11–14 March 2015; SciTePress: Setubal, Portugal, 2015; pp. 262–267. [Google Scholar] [CrossRef]
- Schnürer, R.; Ritzi, M.; Çöltekin, A.; Sieber, R. An empirical evaluation of three-dimensional pie charts with individually extruded sectors in a geovisualization context. Inf. Vis. 2020, 19, 183–206. [Google Scholar] [CrossRef]
- Fischer, M.H. Do irrelevant depth cues affect the comprehension of bar graphs? Appl. Cogn. Psych. 2000, 14, 151–162. [Google Scholar] [CrossRef]
- Zacks, J.; Levy, E.; Tversky, B.; Schiano, D.J. Reading bar graphs: Effects of extraneous depth cues and graphical context. J. Exp. Psychol. Appl. 1998, 4, 119–138. [Google Scholar] [CrossRef]
- Bleisch, S.; Dykes, J.; Nebiker, S. Evaluating the Effectiveness of Representing Numeric Information Through Abstract Graphics in 3D Desktop Virtual Environments. J. Cartogr. 2008, 45, 216–226. [Google Scholar] [CrossRef]
- Ware, C. Visual Thinking for Design; Morgan Kaufmann: Cambridge, UK, 2008. [Google Scholar]
- Munzner, T. Visualization Analysis and Design; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Ware, C. Information Visualization: Perception for Design; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Büschel, W.; Reipschläger, P.; Langner, R.; Dachselt, R. Investigating the Use of Spatial Interaction for 3D Data Visualization on Mobile Devices. In Proceedings of the 2017 ACM International Conference on Interactive Surfaces and Spaces, Brighton, UK, 17–20 October 2017; Association for Computing Machinery: New York, NY, USA, 2017; pp. 62–71. [Google Scholar] [CrossRef]
- Saket, B.; Endert, A. Demonstrational Interaction for Data Visualization. IEEE Comput. Graph. Appl. 2019, 39, 67–72. [Google Scholar] [CrossRef] [PubMed]
- St. John, M.; Cowen, M.B.; Smallman, H.S.; Oonk, H.M. The Use of 2D and 3D Displays for Shape-Understanding versus Relative-Position Tasks. Hum. Factors 2001, 43, 79–98. [Google Scholar] [CrossRef] [PubMed]
- Wilke, C.O. Fundamentals of Data Visualization: A Primer on Making Informative and Compelling Figures; O’Reilly Media: Sebastopol, CA, USA, 2019. [Google Scholar]
- McKenna, S.; Mazur, D.; Agutter, J.; Meyer, M. Design Activity Framework for Visualization Design. IEEE Trans. Vis. Comput. Graph. 2014, 20, 2191–2200. [Google Scholar] [CrossRef] [PubMed]
- Cairo, A. The Truthful Art; New Riders: Indianapolis, IN, USA, 2016. [Google Scholar]
- An, H.; Kim, J.; Sheng, B.; Li, P.; Jung, Y. A transfer function optimization using visual saliency for region of interest-based direct volume rendering. Displays 2023, 80, 102531. [Google Scholar] [CrossRef]
- Norman, D. The Design of Everyday Things: Revised and Expanded; Basic Books: New York, NY, USA, 2013. [Google Scholar]
- Norman, D. Some Observations on Mental Models. In Mental Models; Gentner, D., Stevens, A.L., Eds.; Psychology Press: New York, NY, USA, 1983; pp. 7–14. [Google Scholar] [CrossRef]
- Vila, J.; Gomez, Y. Extracting business information from graphs: An eye tracking experiment. J. Bus. Res. 2016, 69, 1741–1746. [Google Scholar] [CrossRef]
- Okan, Y.; Galesic, M.; Garcia-Retamero, R. How People with Low and High Graph Literacy Process Health Graphs: Evidence from Eye-tracking. J. Behav. Decis. Mak. 2015, 29, 271–294. [Google Scholar] [CrossRef]
- Poirier, M.W.; Decker, C.; Spertus, J.A.; McDowd, J.M. What eye-tracking methods can reveal about the role of information format in decision-aid processing: An exploratory study. Patient. Educ. Couns. 2019, 102, 1977–1984. [Google Scholar] [CrossRef] [PubMed]
- Bylinskii, Z.; Borkin, M.A.; Kim, N.W.; Pfister, H.; Oliva, A. Eye Fixation Metrics for Large Scale Evaluation and Comparison of Information Visualizations. In Eye Tracking and Visualization; Burch, M., Chuang, L., Fisher, B., Schmidt, A., Weiskopf, D., Eds.; Springer: Cham, Switzerland, 2017; pp. 235–255. [Google Scholar] [CrossRef]
- Woller-Carter, M.M.; Okan, Y.; Cokely, E.T.; Garcia-Retamero, R. Communicating and Distorting Risks with Graphs: An Eye-Tracking Study. In Proceedings of the Human Factors and Ergonomics Society Annual Meeting, Canberra, Australia, 11–14 November 2012; pp. 1723–1727. [Google Scholar] [CrossRef]
- Goldberg, J.; Helfman, J. Eye tracking for visualization evaluation: Reading values on linear versus radial graphs. Inf. Vis. 2011, 10, 182–195. [Google Scholar] [CrossRef]
- Goldberg, J.H.; Helfman, J.I. Comparing information graphics: A critical look at eye tracking. In Proceedings of the 3rd BELIV’10 Workshop: BEyond Time and Errors: Novel Evaluation Methods for Information Visualization, Atlanta, Georgia, 10–11 April 2010; Association for Computing Machinery: New York, NY, USA, 2010; pp. 71–78. [Google Scholar] [CrossRef]
- Strobel, B.; Saß, S.; Lindner, M.A.; Köller, O. Do Graph Readers Prefer the Graph Type Most Suited to a Given Task? Insights from Eye Tracking. J. Eye Mov. Res. 2016, 9, 1–15. [Google Scholar] [CrossRef]
- Brehmer, M.; Munzner, T. A multi-level typology of abstract visualization tasks. IEEE Trans. Vis. Comput. Graph. 2013, 19, 2376–2385. [Google Scholar] [CrossRef] [PubMed]
- Barry, C.; Hogan, M.; Lang, M. Heat Maps from Decision Flaps—What We See and What We Think. In Advances in Information Systems Development; Insfran, E., Gonzales, F., Abrahao, S., Fernandez, M., Barry, C., Lang, M., Linger, H., Schneider, C., Eds.; Springer: Cham, Switzerland, 2022; pp. 127–142. [Google Scholar] [CrossRef]



| Bar1 | Bar2 | Bar3 | Bar4 | |
|---|---|---|---|---|
| Control variant | ||||
| Bar1_contr | Bar2_contr | Bar3_contr | Bar4_contr | |
| N | 30 | 30 | 30 | 30 |
| SE (%) | 6.70% | 23.30% | 3.30% | 13.30% |
| ACC (%) | 93.30% | 76.70% | 96.70% | 87.70% |
| Experimental variant | ||||
| Bar1_exper | Bar2_exper | Bar3_exper | Bar4_exper | |
| N | 46 | 46 | 46 | 46 |
| SE (%) | 6.50% | 13.00% | 8.70% | 43.50% |
| ACC (%) | 93.50% | 87.00% | 91.30% | 56.50% |
| What Visualization Did You Use? | Compare the Two Visualizations and Answer. | ||
|---|---|---|---|
| 2D (Group_contr) | 3D (Group_exper) | Pie | |
| N | 62 | 5 | 76 |
| SE (%) | 19.40% | 20.00% | 11.80% |
| ACC (%) | 80.60% | 80.00% | 88.20% |
| Bar1 | Bar2 | Bar3 | Bar4 | |||||
|---|---|---|---|---|---|---|---|---|
| Control variant | ||||||||
| incorrect | correct | incorrect | correct | incorrect | correct | incorrect | correct | |
| N | 2 | 28 | 7 | 23 | 1 | 29 | 4 | 26 |
| E | 2.0 | 28.0 | 5.1 | 24.9 | 2.0 | 28.0 | 9.5 | 20.5 |
| Experimental variant | ||||||||
| N | 3 | 43 | 6 | 40 | 4 | 42 | 20 | 26 |
| E | 3.0 | 43.0 | 7.9 | 38.1 | 3.0 | 43.0 | 14.5 | 31.5 |
| χ2 | 0.001 | 1.356 | 0.850 | 7.637 | ||||
| 2 cells (50.0%) have an expected count of less than 5. The minimum expected count is 1.97. | 0 cells (0.0%) have an expected count of less than 5. The minimum expected count is 5.13. | 2 cells (50.0%) have an expected count of less than 5. The minimum expected count is 1.97. | 0 cells (0.0%) have an expected count of less than 5. The minimum expected count is 9.47. | |||||
| df | 1 | 1 | 1 | 1 | ||||
| p | 1.000 | 0.351 | 0.351 | 0.351 | ||||
| Fisher’s exact test | 1.000 | 0.351 | 0.351 | 0.351 | ||||
| φ | 0.351 | |||||||
| Bar1 | Bar2 | Bar3 | Bar4 | |
|---|---|---|---|---|
| ρ | 0.003 | 0.134 | −0.106 | −0.317 |
| p | 0.980 | 0.250 | 0.363 | 0.005 |
| N | 76 | 76 | 76 | 76 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Svalina, A.; Banić, D.; Kovačević, D. Interpreting Bar Charts: Effects of 3D Depth Cues on Human Gaze and User Understanding. Digital 2024, 4, 932-946. https://doi.org/10.3390/digital4040046
Svalina A, Banić D, Kovačević D. Interpreting Bar Charts: Effects of 3D Depth Cues on Human Gaze and User Understanding. Digital. 2024; 4(4):932-946. https://doi.org/10.3390/digital4040046
Chicago/Turabian StyleSvalina, Ana, Dubravko Banić, and Dorotea Kovačević. 2024. "Interpreting Bar Charts: Effects of 3D Depth Cues on Human Gaze and User Understanding" Digital 4, no. 4: 932-946. https://doi.org/10.3390/digital4040046
APA StyleSvalina, A., Banić, D., & Kovačević, D. (2024). Interpreting Bar Charts: Effects of 3D Depth Cues on Human Gaze and User Understanding. Digital, 4(4), 932-946. https://doi.org/10.3390/digital4040046







