Abstract
Drill bit failure is a prominent concern in the drilling process of any mine, as it can lead to increased mining costs. Over the years, the detection of drill bit failure has been based on the operator’s skills and experience, which are subjective and susceptible to errors. To enhance the efficiency of mining operations, it is necessary to implement applications of artificial intelligence to produce a superior method for drill bit monitoring. This research proposes a new and reliable method to detect drill bit failure in rotary percussion drills using deep learning: a one-dimensional convolutional neural network (1D CNN) with time-acceleration as input data. 18 m3 of granite rock were drilled horizontally using a rock drill and intact tungsten carbide drill bits. The time acceleration of drill vibrations was measured using acceleration sensors mounted on the guide cell of the rock drill. The drill bit failure detection model was evaluated on five drilling conditions: normal, defective, abrasion, high pressure, and misdirection. The model achieved a classification accuracy of 88.7%. The proposed model was compared to three state-of-the-art (SOTA) deep learning neural networks. The model outperformed SOTA methods in terms of classification accuracy. Our method provides an automatic and reliable way to detect drill bit failure in rotary percussion drills.
1. Introduction
Drilling is of the utmost importance in underground mining and surface mining, since minerals are extracted from the earth’s surface by drilling blast holes in hard rock using rotary percussion drilling methods. Often, a button bit is used in rotary percussion drilling. The bit consists of a flushing hole to remove cuttings, and buttons which interact with the drilling surface. Rock failure is facilitated via the employment of a piston which delivers rapid impacts to the drill stems, thereby transferring energy to the drill bit. The downhole blows to the rock are delivered by the bit while a rotational device ensures that the bit impacts a new rock surface with each blow. This drilling method can be employed in both hard and soft rocks [1]. Because of its good drilling depth and diameter, the method is most suitable for underground mining. Abnormalities often occur during drilling, such as wear and abrasion of the drill bit buttons due to excessive feed force and deviation of the drill hole trajectory. These abnormalities decrease drilling efficiency and increase drilling costs; for instance, cracks in the drill bit can cause thermal complications leading to loosening of the bit and rod, which often results in other parts such as the rod and shank failing [2]. These abnormalities are often detected by operators based on their sensory judgment and experience, which is an unreliable method of detecting drill bit failure. Hence, the operating costs of this drilling method are likely to vary depending on the operator’s skill and experience, making continuous failure monitoring of drill bits an important requirement in the quest to reduce operating costs.
Drill wear monitoring in the mining industry is well established. A study by Gradl et al. [3] proved that bit characterization during drilling can be determined by the noise produced from drill bits. Data were collected using a standard microphone and frequency analysis was performed to determine the condition of the bit. Karakus & Perez [4] also established that acoustic emission monitoring techniques are a feasible option to optimize diamond core drilling performance and changes in drilling conditions. Acoustic emission sensors were attached to both the drill and the rocks to record acoustic signals being emitted during drilling. Acoustic emission waveforms were analyzed, and the results revealed that acoustic emission amplitudes decrease as wear begins to accelerate. Kawamura et al. [5] used a GoPro camera to capture the sounds generated during drilling. Signal processing techniques such as time series analysis, Fast Fourier transform, and Wavelet transform were used to find the failure of button bits. The results proved that sounds produced during drilling can be used to detect the condition of drill bits. However, the use of microphones and other acoustic emission sensors have limitations such as directional consideration and environmental sensitivity. Acoustic signals are very sensitive to noise ingress. Sound measurements are more vulnerable to noise ingress than vibration measurements [6]. Due to the nature of vibration signals, they are considered to contain reliable features for monitoring drill wear, as the vibrating drill length in the transverse and axial modes does not change during drilling, thus maintaining a constant mode of frequency [7]. For these reasons, vibration measurement was considered for this research. The study aimed to build a cost-effective and easy-to-implement system that could be easily adopted and reproduced by mines and other researchers, hence the use of accelerometers to measure drill vibrations. In a recent study done by Uğurlu [8], he proposed a statistical analysis and model for drill bit management in open pit mining operations. The model was formulated by collecting operational parameters such as rotational speed, drilling time, and drilling energy. The results showed that the proposed system could be used for drill bit monitoring. Across these studies, it is evident that drill bit monitoring is of utmost importance; nevertheless, the methods are lagging, laborious, and non-automatic. In mining engineering, the adoption of machine learning has been uneven. Jung & Choi [9] conducted a study to review research papers published over the last decade that discuss machine learning techniques for mineral exploration, exploitation, and mine reclamation. The results showed that machine learning studies have been actively conducted in the mining industry since 2018 and that most were for mineral exploration. Support vector machines were utilized the most, followed by deep learning models. Only 7% of the studies employed convolutional neural network (CNNs). This only proves that when it comes to artificial intelligence, the mining field, especially in exploitation, is lagging compared to other fields such as the petroleum exploration and production (P&E) field, as well as the medical field. Most studies that utilize machine learning to monitor the condition of drill bits during drilling have been conducted in the manufacturing and P&E industry [10,11,12,13,14]. Although the drilling techniques in these industries are different from those of the mining industry, this study believes that some concepts should be adopted and mirrored to enhance the efficiency of drilling operations in the mining industry.
Recently, many studies have been dedicated to working on automatic solutions to accurately detect and identify any damage to various machine parts. Among the available approaches, vibration-based and machine learning techniques have proven to be the most effective and reliable in revealing and quantifying damage in rotating machinery [15]. Eren [16] proposed an adaptive implementation of one-dimensional (1D) CNN for bearing health monitoring. The proposed system combines feature extraction and classification into a single learning body. The convolutional layers of the proposed 1D CNN learn to extract optimized features from raw data. Since the raw bearing vibration data is directly fed into the proposed system, the computational burden due to feature extraction is eliminated. The 1D CNN fault detection model had an accuracy of over 97%. In another study, Ince et al. [17] proposed a method based on a compact 1D CNN to detect a potential motor anomaly due to bearing faults. The 1D CNN was able to detect anomalies in real-time at approximately 100% accuracy. Due to the success of these studies, this study proposes a novel and reliable method to detect drill bit failure in rotary percussion drills using 1D CNN due to its robustness, unique abilities to optimize both feature extraction and classification in a single learning body, minimal data pre-processing abilities, and low computational complexity that allows real-time monitoring.
Figure 1 shows the proposed drill bit failure detection system design. The system comprises accelerometers installed on the guide cell of the rock drifter to capture vibration signals from drilling. Vibration signals are then used as input to a 1D CNN network. After training and evaluating different models, the best model is then selected as the drill bit failure detection system. The application of this proposed system in the mining site can help drill rig operators and mining engineers identify possible drill bit failures, thereby minimizing mining costs and increasing the productivity of the mine.
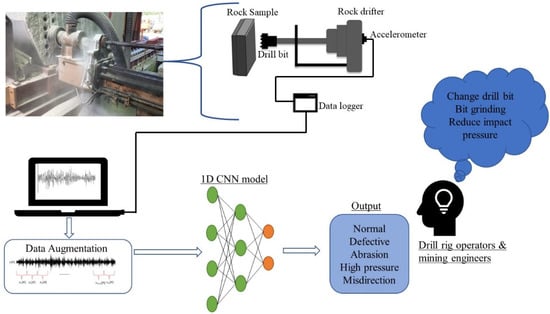
Figure 1.
Overview of the proposed drill bit failure detection system. Accelerometers are used to collect drill vibration data, after which data augmentation is done to increase the data samples. The 1D CNN network is then trained and evaluated to obtain the best model for drill bit failure detection.
In summary, the main contributions of this paper are as follows:
- A reliable, automatic, and cost-effective method to monitor drill bit failures using machine learning. The use of accelerometers allows for easy installation and removal. Accelerometers can be used with any drilling machine, thereby making the system easy to adopt and implement. 1D CNN has the advantage of processing and analyzing complex tasks in a short time, which allows the automation of decision making, therefore eliminating the unreliable method used by drill rig operators.
- Compared to other fault diagnosis studies which are based on heavy data pre-processing and are limited to two classifications, normal and failure, this paper presents a system that requires minimal data pre-processing, making it easy to implement in real-time. The system also classifies five conditions: normal, defective, abrasion, high impact pressure, and misdirection.
- The application of a longer kernel size that is approximately ¼ the size of the input signal effectively improves the accuracy of the drill bit failure detection model.
The chapters of this paper are arranged as follows. In Section 2, the one-dimensional convolutional neural network for time series classification is briefly described. Section 3 explains data acquisition and state-of-the-art (SOTA) models used in time series classification. Section 4 describes the proposed 1D CNN architecture and the selection of model hyperparameters. Section 5 shows the generalization abilities of the proposed model and the comparison with SOTA models. Finally, Section 6 presents the conclusion.
2. 1D CNN for Time Series Classification
CNNs were developed with the idea of local connectivity. Each node is connected only to a local region in the input. The local connectivity is achieved by replacing the weighted sums from the neural network with convolutions [18]. A convolution applies and slides a filter over the time series. Unlike images, the filters exhibit only one dimension (time) instead of two dimensions (width and height). The result of a convolution (one filter) on an input time series can be considered as another univariate time series that underwent a filtering process. Thus, applying several filters on a time series will result in a multivariate time series whose dimensions are equal to the number of filters used. Applying several filters on an input time series helps the network learn multiple discriminative features useful for the classification task. Instead of manually setting the values of the filter, the values are learned automatically, since they highly depend on the targeted dataset. To automatically learn a discriminative filter, the convolution should be followed by a discriminative classifier, which is usually preceded by a pooling operation that can either be local or global. Local pooling, such as average or max pooling, takes an input time series and reduces its length by aggregating over a sliding window of the time series. With a global pooling operation, the time series will be aggregated over the whole-time dimension resulting in a single real value. Some deep learning architectures include normalization layers to help the network converge quickly. For time-series data, the batch normalization operation is performed over each channel, therefore preventing internal covariate shift across one mini-batch training of time series. The final discriminative layer takes the representation of the input time series (the result of the convolutions) and gives a probability distribution over the class variables in the dataset. Usually, this layer is comprised of a softmax operation. In some approaches, an additional non-linear fully connected layer is added before the final softmax layer. Finally, to train and learn the parameters of a deep CNN: a feed-forward pass followed by backpropagation is done [19].
3. Materials and Methods
3.1. Data Description
During drilling, drill buttons are in contact with the rock surface under intense pressures, which can lead to wear of the buttons. Vertical thrust force has a large impact on the rate of penetration and the wearing of bits [20]. The wearing of drill bit buttons significantly affects their service lives and machine operating costs. Therefore, continuous failure analysis is required to reduce operating costs [2]. Most research on machine fault diagnosis is limited to two conditions: the healthy state and the faulty state. The classification problem is limited to only two classes. Because there are numerous failures associated with drill bits, we aimed to detect two types of failures and two drilling conditions that lead to drill bit failure. We divided the categories into 5 conditions: normal, defective, abrasion, high impact pressure, and misdirection.
Under the normal condition, a healthy drill bit was used: a normal bit that had undamaged buttons with a high protrusion height. Figure 2a shows a normal bit used in this study. Under the defective condition, some of the buttons in the bit were completely broken, off as indicated by Figure 2b. This type of failure is often caused by the free hammering of the bit in the air and improper soldering of the buttons in a bit base steel [2]. Under the abrasion condition, the drill buttons were completely worn out as shown in Figure 2c. This type of failure is caused by overused drill bits. If the diameter of the flat face of the bit button is larger than one-third of the original button diameter, then the bit is classified as overused. The continued use of an overused bit can lead to adverse effects on tool efficiency and trigger drill hole deviations [2]. If excessive impact pressure is applied to the bit, it is likely to cause failure to the bit. Excessive bit load can affect the constancy of drill rotation, which can cause drill hole deviation leading to poor rock fragmentation, which can damage drill bits. It is important for drill rig operators to identify excessive impact pressure and drill hole deviation (misdirection) to avoid further damage to the bit. Normal bits were used to measure drill vibrations for high impact pressure and misdirection.

Figure 2.
Tungsten carbide drill bits used for drilling: (a) normal bit, (b) chipped button bit (defective), (c) worn-out bit (abrasion).
3.2. Data Acquisition
An acceleration sensor was mounted on the guide cell of the rock drill to detect vibration signals in the longitudinal direction. It was mounted such that the desired measuring direction coincided with its main sensitivity axis. The sensor could detect the vibration behavior of the drill bit, as the vibrations from the bit propagated through the drill string to the body of the drill machine. The outline and schematic diagram of the experiment are shown in Figure 3. Drilling was performed on a granite rock and drill vibrations were measured. The drilling conditions are shown in Table 1: normal, defective, abrasion, high impact pressure, and misdirection. 10 holes were drilled for each condition, in total 50 holes were drilled. The length of one drill hole was approximately 1 m. The number of hits per minute was set at 3120 for all holes. Table 2 illustrates the data acquisition parameters used for the experiment. The impact pressure for each hole was set at 13.5-7 MPa. The striking frequency, the number of revolutions, and the drilling speed were determined by the striking pressure, the rotating pressure, and the feed pressure. The rotation pressure was 4–6 MPa and the feed pressure was 4 MPa. The sampling frequency was set at 50 kHz. The accelerometer (TEAC’s piezoelectric acceleration transducer 600 series) was a charge capacity type that measured time acceleration in the longitudinal direction. The maximum acceleration used by the sensor was ±10,000 m/s². The acceleration sensor output a voltage that was then transmitted to the data logger (GRAPHTEC Data Platform DM3300). The data logger had a built-in amplifier; the acceleration was written out as CSV data on the PC by inputting the calibration coefficient of the acceleration sensor into the data logger.

Figure 3.
Experimental setup. 18 m3 of granite rock was horizontally drilled using a stationary rock drifter with accelerometers mounted on the guide cell of the rock drifter. Acceleration data was transmitted from the accelerometers to the data logger and then stored in the PC as CSV data.

Table 1.
Experimental conditions.

Table 2.
Parameters of the experiment.
3.3. Data Preprocessing
CNNs require a large amount of data for training and testing; hence, data augmentation was performed to increase the number of data sets to improve the accuracy of the CNN model. Sampling frequency, sampling time, and sampling number were taken into consideration for data augmentation. The sampling frequency was set at 50 kHz with a sampling time of 60 s; using Equation (1), each drill hole had approximately 3,000,000 sampling numbers (data points). Each test drill hole signal was divided into approximately 1000 segments each with 3000 data points with no overlapping. Figure 4 depicts the data augmentation process. Each segmentation had a fixed length of 0.06 s, which guaranteed that at least 3 drill bit hits were represented within one segment. Each drill condition had 9000 test samples to be used for training, validating, and testing the 1D CNN model.
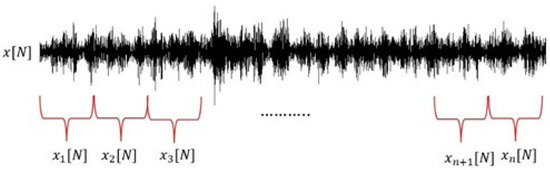
Figure 4.
Data augmentation: the original waveform was sectioned into 0.06 s segments to increase the amount of data for 1D CNN training, validating, and testing.
3.4. State of the Art Deep Learning Neural Networks
Three fundamental deep learning neural networks (DNNs) for time series classification as described by Fawaz et al. [19] were selected to compare with the proposed drill bit failure detection model (DBFD). Figure 4 shows the network structure of the three neural networks [21].
3.4.1. Multilayer Perceptron (MLP)
MLPs are the most traditional form of DNNs. They were described as a baseline architecture for time series classification by Wang et al. [21]. The network has four layers; each is fully connected to the output of its previous layer. The three fully connected layers have 500 neurons followed by dropout at each layer’s input, to improve the generalization capability. The rectified linear unit (ReLU) is used as an activation function to prevent saturation of the gradient when the network is deep. The network ends with a softmax layer. The dropout rates at the input layer, hidden layers, and the softmax layer are 0.1, 0.2, and 0.3, respectively, as shown in Figure 5a.
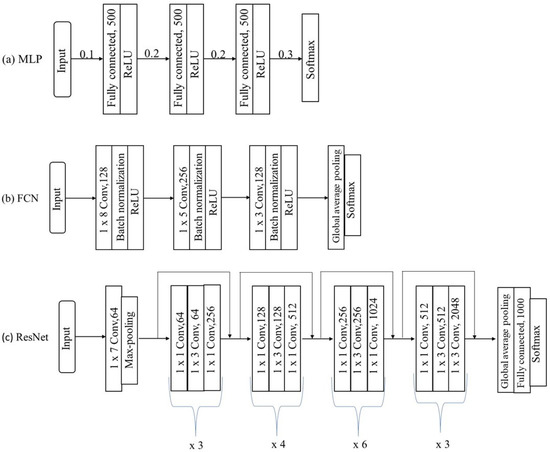
Figure 5.
The architecture of three SOTA DNNs: (a) MLP; (b) FCN; (c) ResNet 50.
3.4.2. Fully Connected Layers (FCN)
FCNs are mainly convolutional networks that do not contain any local pooling layers, which means that the length of the time series is kept unchanged throughout the convolutions. The basic block is a convolutional layer followed by a batch normalization layer and a ReLU activation layer. The convolution operation is fulfilled by three 1-D kernels with the sizes 8, 5, and 3, with no striding operator. Three convolution blocks are stacked with the filter sizes of 128, 256, and 128 in each block. Local pooling operation is not applied to prevent overfitting. Batch normalization is applied to speed up the convergence speed and to help improve generalization. After the convolution blocks, the features are fed into a global average pooling (GAP) layer instead of a fully connected layer, which largely reduces the number of weights [21]. The final label is produced by a softmax layer. The architecture of FCN is shown in Figure 5b.
3.4.3. Residual Network (ResNet 50)
The main characteristic of ResNet is the shortcut residual connection between consecutive convolutional layers. The architecture of ResNet is depicted in Figure 5c. The difference with the usual convolutions, such as in FCNs, is that a linear shortcut is added to link the output of a residual block to its input, thus enabling the flow of the gradient directly through these connections, which makes training a DNN much easier by reducing the vanishing gradient effect [22]. The network is composed of 16 residual blocks followed by a GAP layer and a final softmax classifier, whose number of neurons is equal to the number of classes in a dataset. Each residual block is composed of three convolutions whose output is added to the residual block’s input and then fed to the next layer. The number of filters for each residual block differs as shown in Figure 5c. In each residual block, the filter’s length is set to 1, 3, and 1, respectively. The final residual block is followed by a global average pooling layer and a softmax layer [21].
3.5. Experiment Implementation Details
To run all experiments, five classes were used: normal, defective, abrasion, high pressure, and misdirection. Under each condition, 9000 data were prepared. The data was split into 70% training (6300), 15% Validation (1350), and 15% testing (1350). All models were trained with Adam as an optimizer and a learning rate of 0.001. A batch size of 128 and 25 epochs were selected. The training process was conducted by MATLAB R2020b with a deep learning toolbox. The machine specifications are summarized in Table 3.

Table 3.
Machine specifications.
3.6. Evaluation Metrics
The models were evaluated by analyzing how well they perform on test data. Confusion matrices were used to show the summary of the prediction results made by the models on test data. The confusion matrix indicates the true label and the false label made by the model for each class. In the confusion matrix, true positives (TP) are positive cases, and the prediction is correct. False positives (FP) are negative cases that are misclassified as positive. True negative (TN) are negative cases that are correctly classified as negative. False negatives (FN) are positive cases that are misclassified as negative. Due to class-balanced confusion matrices, accuracy was used as the main performance metric to evaluate the models. Accuracy summarizes the performance of a classification model as the number of correct predictions divided by the total number of predictions, as indicated by Equation (2). Other measurement metrics used to explain the confusion matrix were sensitivity or recall, which correspond to the accuracy of positive examples, as can be calculated with Equation (3). Precision measures the correctness of the model; it is defined as the number of true positives divided by the number of true positives plus the number of false positives as shown by Equation (4).
where TP refers to the true positives, TN refers to the true negatives, FP refers to the false positives, and FN refers to the false negatives.
4. Proposed Drill Bit Failure Detection (DBFD) Model 1D CNN Architecture
Recent studies show that time series classification 1D CNNs with relatively shallow architectures can learn challenging tasks involving 1D signals [15]; therefore, a simple and compact CNN architecture was constructed. The proposed 1D CNN model was inspired by Time Le-Net (t-LeNet) model, which was originally made famous by Guennec et al. [23]. The t-LeNet model has two convolutional layers, followed by a fully connected layer and a softmax classifier. The model utilizes a local max pooling operation as a way of achieving translation invariance. A similar CNN architecture was adopted, but hyperparameter alterations were made to suit our dataset. The proposed CNN architecture shown in Figure 6 comprises two pairs of convolutional and max pooling layers, two fully connected layers, and a softmax layer. The last fully connected layer combines features to classify signals; therefore, the output size argument of the last fully connected layer is equal to the number of classes of the data set. As shown in Table 4, the first convolutional layer has a kernel size of 751 with 128 filters and a stride of 2. The second convolutional layer has a kernel size of 281 with 128 filters and a stride of 2. Batch normalization and leaky ReLU were applied after each convolutional layer, before max pooling to speed up the convergence and to help improve generalization. The proposed model had a total of 31,515,805 learnable parameters.
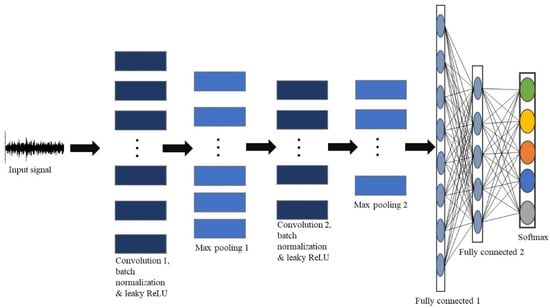
Figure 6.
A simple and compact 1D CNN architecture for the DBFD model.

Table 4.
Proposed DBFD model’s parameters.
The performance of a CNN model is highly dependent on its hyperparameters. Hyperparameter optimization is not a simple task, as it is problem specific. According to Zhao et al. [24], the kernel size, pooling method, pooling size, and the number of convolution filters are important hyperparameters in time series classification. In this study, hyperparameters were tuned manually by trial and error. A set of experiments were conducted to determine the optimum hyperparameters for the DBFD model before selecting the proposed model’s parameters, shown in Table 4.
4.1. Kernel Size
The convolutional kernels (filters) represent the local features of the input time series. If the kernel size is too small, it cannot represent the typical features of waveforms well. It will have difficulty reflecting local features concisely, and an over-length kernel size will bring extra noise into the representation, therefore reducing the quality of feature representation [24]. There are unresolved challenges with kernel size selection; different approaches have been proposed but no agreement on which is best [25]. It is common practice to use kernel sizes of 1 × 3 or 1 × 5. If a narrow kernel size of 1 × 3 is adopted, each output feature value can obtain only the feature relationship among the adjacent three values of the input signal, which will greatly limit the network’s ability to learn low-frequency signal features. However, the introduction of a wide convolutional kernel allows one convolution operation to obtain the feature relationship in a longer sequence [26]. We propose a kernel size of 1 × 751 and 1 × 281 for the first and second convolutional layers. For the first convolution layer, an odd number that was greater than or equal to K in Equation (5) was used as kernel size. Equation (6) was then used to calculate the output shape of the first convolutional and pooling layer. The shape from the first pooling layer was used as an input shape to the second convolutional layer. Equation (5) was then used to obtain the kernel size for the second convolutional layer. We believe that using a kernel size that is at least ¼ the size of the input waveform allows for the receptive field to be long enough to catch positional information within the signal.
where X is the output shape, N is input (data length), K is the kernel size, P is padding, and S is the stride.
A set of experiments were conducted to prove that the proposed kernel size had a better abstraction of features compared to commonly used kernel sizes. Table 5 shows the training and validation accuracy of different kernel sizes. The proposed kernel size performs better than the commonly used filter sizes in terms of training accuracy and validation accuracy. Figure 7 shows the learning curve of training accuracy for all kernel sizes. The training learning curves were evaluated to understand how well the models were learning. The proposed kernel size curve had a steadier curve compared to the other kernel sizes. This proves that the use of a longer kernel size offers better feature learning abilities for our data.

Table 5.
Training and validation loss of commonly used kernel sizes and the proposed kernel size.
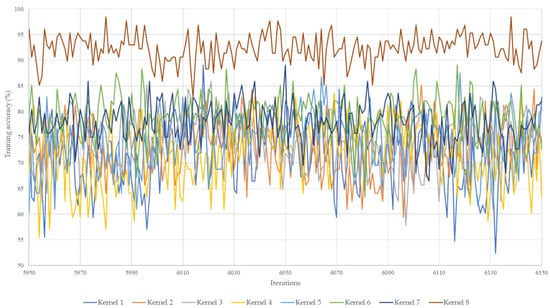
Figure 7.
Training accuracy learning curve for all kernel sizes. The Y-axis shows the training accuracy in percentage and the X-axis indicates the iterations from iteration 5950 to 6150.
4.2. Pooling Method and Size
The purpose of the pooling operation is to achieve dimension reduction of feature maps while preserving important information. Max pooling and Mean pooling are commonly used pooling methods in CNN. Mean pooling calculates the mean value of the parameter within the range following the predetermined pooling window size, while max pooling selects the largest parameter within the predetermined window range as the output value [27]. Local max pooling was selected for local translation invariance purposes. The pooling size is also an important parameter to be decided beforehand. The larger the pooling size is, the better the performance it obtains in dimension reduction, but the more information it loses [24]. Experiments were carried out to determine the suitable pooling size for the DBFD model. From the results of these experiments shown in Table 6, a filter size of 3 and 5 offered a better validation accuracy compared to the other filter sizes. A filter size of 3 was selected as it had a slightly better validation accuracy than a filter size of 5.

Table 6.
Training and validation accuracy for different pooling sizes.
4.3. Number of Convolution Filters
The filters represent the local features of a time series. A few filters cannot extract discriminative features from the input data to achieve a higher generalization accuracy, but having more filters is computationally expensive [24]. In general, the number of filters increases as a CNN network grows [28]. Experiments were conducted to select the best possible number of filters to adopt. Table 7 indicates the training accuracy, validation accuracy, and computation time for three different models with different filter numbers. Using 128 filters in the first and second convolutional layer produced a higher validation accuracy of 89.02%. It was observed that with the increase of filters the computational time also increased. A filter size of 128 in both convolutional layers was adopted, as it offered a better validation accuracy.

Table 7.
Training and validation accuracy of different convolution filter numbers.
4.4. Evaluation of Network Depth on the Performance of the DBFD Model
The representational capacity of a CNN usually depends on its depth; an enriched feature set ranging from simple to complex abstractions can help in learning complex problems. However, the main challenge faced by deep architectures is that of the diminishing gradient [29]. Numerous studies on 1D CNN time series classification have proposed and proved that a simple configuration 1D CNN with two or three layers is capable of achieving higher learning, and that sometimes a deep and complex CNN architecture is not necessary to achieve high detection rates for time series classification [16]. The effects of network depth on the performance of the model were studied: DBFD 2 which had two layers, DBFD 3 which had three layers, and DBFD 4 which had four layers. Table 8 shows the training and validation accuracy of the three models. The performance of the DBFD model is relatively the same as the network depth increases. DBFD 2 had a 0.53% and 0.08% higher validation accuracy than DBFD 3 and DBFD 4. DBFD 2 was selected as it offered a slightly better validation accuracy than other models.

Table 8.
Performance of the DBFD model under different network depth.
To gain insight into the classification abilities of the DBFD 2 model, the t-distributed stochastic neighbor embedding method (t-SNE) was used to visualize the network’s activations on the validation data set. t-SNE is one of the dimension compression algorithms used for the visualization of high-dimensional data. t-SNE works by creating a probability distribution that dictates the relationship between various neighboring points. It then recreates a low dimensional space that follows the probability distribution of the data as much as possible [30]. Visualization allows the finding of points that appear in the wrong cluster, indicating an observation that the network misclassified. 1350 data from each condition were compressed into a two-dimensional map and visualized. Tight clusters in the t-SNE plot indicate classes that the model classifies correctly, and outliers show misclassified data. From Figure 8, the early layer conv1 and maxpool1 activations do not exhibit any clustering by class because the layers were operating on low-level features. At conv2 and maxpool2 activations, the normal condition had already started to form clusters, which indicates the model was able to extract important features from the waveform early on. At these layers, the clustering of classes began to form, but not vividly, as there were overlapping data. At FC1 activations, normal, defective, high pressure, and misdirection had formed tight clusters, but the abrasion cluster was not well defined, as there were many overlaps between abrasion–high pressure and abrasion–defective. In the softmax layer, high-level features were extracted from the data. At this layer, the normal, defective, and misdirection classes were well defined, but the normal and high-pressure classes were not as tight, and were circular compared to the previous layer, FC1, because t-SNE tends to expand dense clusters and contracts sparse ones as a way of evening out cluster sizes. The results indicate that a shallow and compact 1D CNN model is capable of high-level feature learning.
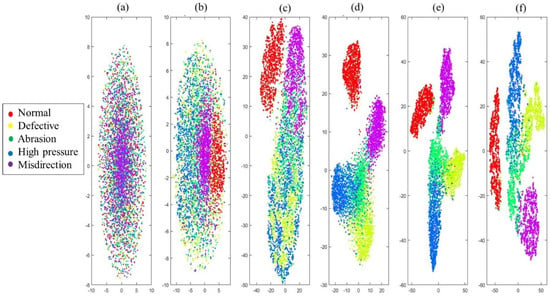
Figure 8.
Visualization of the DBFD model’s activations using the t-distributed stochastic neighbor embedding (t-SNE) method. t-SNE was used to visualize clustering as training occurred in (a) convolution 1, (b) max pooling 1, (c) convolution 2, (d) max pooling 2, (e) fully connected layer 1, and (f) the softmax layer of the DBFD 2 model.
5. Results and Discussions
1D CNN presents an opportunity to predict drill bit failure in rotary percussion drilling with minimum effort. Accurate and efficient models are sought after. First, the proposed DBFD model was evaluated on test data, then a comparison analysis was conducted with SOTA models.
5.1. DBFD Model Evaluation
From the confusion matrix in Figure 9, it can be noted that the normal condition had the highest recall of 99.0%; out of 1350 examples, the model was correct for 1337. Misdirection also had a high recall of 98.4%. Defective and high pressure had a recall of 88.1% and 85.3%, respectively. The model had the lowest recall of 72.5% for abrasion; out of 13,500 examples, it predicted 979 correctly and misclassified 371. In terms of precision, normal and misdirection had the highest precisions, of 96.6% and 92.7%. The results indicate that the model was less precise with the abrasion condition, in which a precision of 80% was attained. The model had a good precision rate of ≥80% in all classes. Overall classification accuracy of 88.7% was achieved, which was satisfactory. Figure 10 shows the false negatives for each target class. It shows the number of misclassified examples between classes. The highest rate of misclassification occurred between the pairs of abrasion–high pressure and abrasion–defective; the model could not differentiate between the acceleration waveforms of these pairs. Another pair that had the most misclassification was defective–high pressure. These three class pairs accounted for more than 70% of all mistakes made by the model. t-SNE was used to visualize the performance of the model on unseen test data. As seen in Figure 11, there was a huge overlap between abrasion–high pressure and abrasion–defective, which implies that the model could not extract valuable features from the abrasion vibration signals to distinguish it from high pressure and defective. We believe that because defective and abrasion both represent a faulty state of the drill bit, they are likely to produce similar vibration signatures, and that is why there was a huge misclassification between defective–abrasion and abrasion–high pressure.
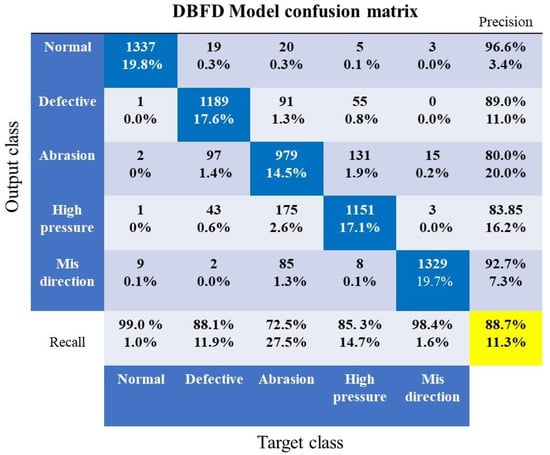
Figure 9.
A confusion matrix used to evaluate the prediction abilities of the drill bit failure detection model on test data.
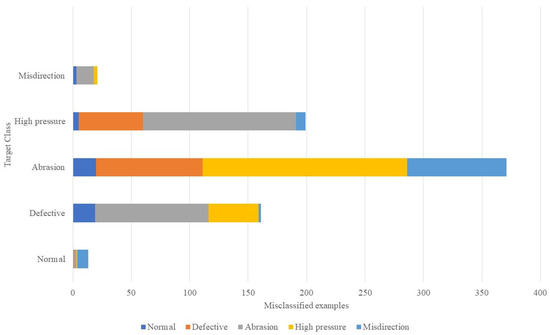
Figure 10.
The number of misclassified examples between classes.
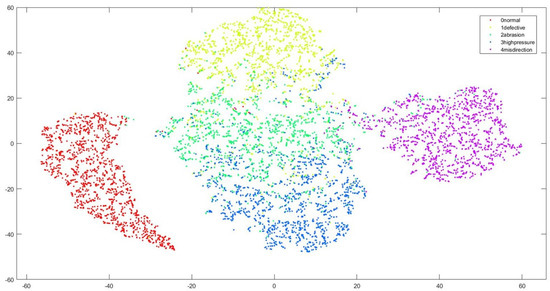
Figure 11.
t-SNE was used to visualize the performance of the DBFD model on test data.
5.2. Comparison with SOTA Models
We selected three deep neural networks that are considered baselines for time series classification, published by Wang et al. [19] and Fawaz et al. [21]: MLP, FCN, and ResNet. The aim was to compare the proposed DBFD model to the SOTA models by evaluating the models using classification accuracy and processing time. There is a significant difference between the architectures of the four models. The proposed model utilizes a longer kernel size and local max pooling, while FCN and ResNet 50 use a shorter kernel size and global average pooling and MLPs employ fully connected layers throughout their architecture. ResNet 50, which is 50 layers deep, was employed to assess if the model’s accuracy will improve when utilizing a deeper network. The training and testing process for all models was carried out using similar experimental conditions, for example, data splitting, number of epochs, and batch size.
Table 9 summarizes the accuracy and processing time of all four models. Processing time was used to evaluate the computational complexity and processing efficiency of the models. The results demonstrate that in terms of classification accuracy, the proposed model performed better than all three SOTA models. The DBFD model had an overall classification accuracy of 88.7%. ResNet model ranked second with a classification accuracy of 81.6%. FCN ranked third with an accuracy of 76.7%. MLP had the lowest classification accuracy of 54.0%, which indicates that the model could not learn distinct patterns to differentiate the five drilling conditions. Based on the computation time it took each model to make classifications, MLP showed the best performance, by taking the shortest time of 170.52 min for 6150 iterations; this is because it has three fully connected layers, each with 500 neurons; therefore, forward and backpropagation can be carried out swiftly. The proposed DBFD model had the shortest processing time of 428.50 min compared to FCN (476.57 min) and Resnet50 (1805.29 min), which implies a better processing efficiency. Resnet had the longest training time because it is 50 layers deep. Figure 12 shows the confusion matrix of the SOTA models. From Figure 12, it can be noted that normal and misdirection had the highest recall and precision in all models compared to other classes. Across all SOTA models, the most misclassifications occurred between the class pairs of abrasion–high pressure and abrasion–defective. The proposed DBFD model outperforms the SOTA models in terms of classification accuracy and processing efficiency, which makes it superior in predicting drill bit failure in rotary percussion drills.

Table 9.
Summary of performance metrics for the proposed model and SOTA models.
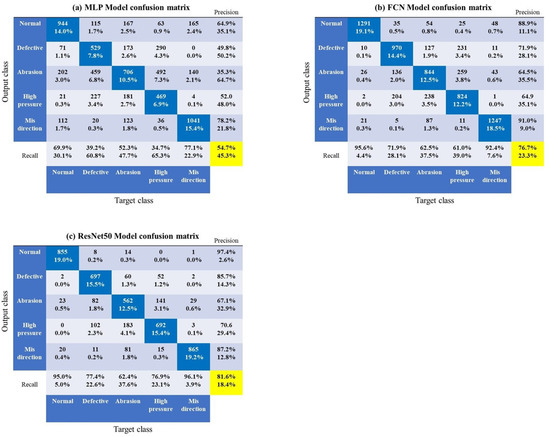
Figure 12.
Confusion matrix showing the classification results from the three SOTA models; (a) MLP model’s confusion matrix, (b) FCN model’s confusion matrix, (c) ResNet50 model’s confusion matrix.
6. Conclusions
Over the years, the detection of drill bit failure has been done by drill rig operators based on the experience and skills they gain over years of drilling. This method is susceptible to human error; hence, a reliable method to detect drill bit failure is needed. This research utilizes drill vibrations and a 1D CNN to build a reliable drill bit failure detection model. Vibration measurement using accelerometers was considered, as we aimed to build a cost-effective and easy-to-implement system. 1D CNN was employed because of its unique abilities to optimize both feature extraction and classification in a single learning body, minimal data pre-processing abilities, and low computational complexity. A two-layered CNN model with 128 filters, a stride of 2, and kernel sizes of 751 and 281 was utilized to classify five drilling conditions: normal, defective, abrasion, high pressure, and misdirection. The model had an overall classification accuracy of 88.7%. The model was able to successfully classify drill conditions with few incorrect predictions. Most of the misclassification errors occurred between the pairs of abrasion–high pressure and abrasion–defective. We showed that the proposed model can achieve better classification accuracy and processing time compared to SOTA models. Our work demonstrates that a simple and compact 1D CNN model which utilizes a longer kernel size than most studies and local pooling is effective in predicting drill bit failure in rotary percussion drilling. In application, the drill bit failure detection model could be used simultaneously with the expertise of drill rig operators. In this study, only one type of rock was considered; in the future, more experiments with different types of rocks need to be conducted.
Author Contributions
Conceptualization, L.S. and Y.K. (Youhei Kawamura); Methodology, L.S., J.S. and Y.K. (Yoshino Kosugi); Software, L.S. and J.S.; Validation, H.T.; Formal Analysis, L.S.; Investigation, L.S.; Resources, M.H.; Data Curation, M.H.; Writing—Original Draft Preparation, L.S.; Writing—Review and Editing, H.T. and Y.K. (Youhei Kawamura); Visualization, Y.K. (Youhei Kawamura); Supervision, Y.K. (Youhei Kawamura); Project Administration, Y.K. (Youhei Kawamura); Funding Acquisition, Y.K. (Youhei Kawamura). All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors would like to show gratitude to the Mitsubishi Materials Corporation for data collection assistance.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sandvik Tamrock Corp. Rock Excavation Handbook; Sandvik Tamrock Corp: Stockholm, Sweden, 1999. [Google Scholar]
- Jang, H. Effects of Overused Top-hammer Drilling Bits. IMST 2019, 1, 555558. [Google Scholar] [CrossRef]
- Gradl, C.; Eustes, A.W.; Thonhauser, G. An Analysis of Noise Characteristics of Drill Bits; ASME: Estoril, Portugal, 2008; p. 7. [Google Scholar]
- Karakus, M.; Perez, S. Acoustic emission analysis for rock–bit interactions in impregnated diamond core drilling. Int. J. Rock Mech. Min. Sci. 2014, 68, 36–43. [Google Scholar] [CrossRef]
- Kawamura, Y.; Jang, H.; Hettiarachchi, D.; Takarada, Y.; Okawa, H.; Shibuya, T. A Case Study of Assessing Button Bits Failure through Wavelet Transform Using Rock Drilling Induced Noise Signals. J. Powder Metall. Min. 2017, 6, 1–6. [Google Scholar] [CrossRef]
- Sikorska, J.Z.; Mba, D. Challenges and obstacles in the application of acoustic emission to process machinery. Proc. Inst. Mech. Eng. Part E J. Process. Mech. Eng. 2008, 222, 1–19. [Google Scholar] [CrossRef]
- Jantunen, E. A summary of methods applied to tool condition monitoring in drilling. Int. J. Mach. Tools Manuf. 2002, 42, 997–1010. [Google Scholar] [CrossRef]
- Uğurlu, Ö.F. Drill Bit Monitoring and Replacement Optimization in Open-Pit Mines. Bilimsel Madencilik Derg. 2021, 60, 83–87. [Google Scholar] [CrossRef]
- Jung, D.; Choi, Y. Systematic Review of Machine Learning Applications in Mining: Exploration, Exploitation, and Reclamation. Minerals 2021, 11, 148. [Google Scholar] [CrossRef]
- Vununu, C.; Moon, K.-S.; Lee, S.-H.; Kwon, K.-R. A Deep Feature Learning Method for Drill Bits Monitoring Using the Spectral Analysis of the Acoustic Signals. Sensors 2018, 18, 2634. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rai, B. A Study of Classification Models to Predict Drill-Bit Breakage Using Degradation Signals. Int. J. Econ. Manag. Eng. 2014, 8, 4. [Google Scholar]
- Gómez, M.P.; Hey, A.M.; Ruzzante, J.E.; D’Attellis, C.E. Tool wear evaluation in drilling by acoustic emission. Phys. Procedia 2010, 3, 819–825. [Google Scholar] [CrossRef] [Green Version]
- Bello, O.; Teodoriu, C.; Yaqoob, T.; Oppelt, J.; Holzmann, J.; Obiwanne, A. Application of Artificial Intelligence Techniques in Drilling System Design and Operations: A State of the Art Review and Future Research Pathways. In Proceedings of the SPE Nigeria Annual International Conference and Exhibition, Lagos, Nigeria, 2–4 August 2016. [Google Scholar] [CrossRef]
- Lashari, S.E.Z.; Takbiri-Borujeni, A.; Fathi, E.; Sun, T.; Rahmani, R.; Khazaeli, M. Drilling performance monitoring and optimization: A data-driven approach. J. Petrol. Explor. Prod. Technol. 2019, 9, 2747–2756. [Google Scholar] [CrossRef] [Green Version]
- Kiranyaz, S.; Avci, O.; Abdeljaber, O.; Ince, T.; Gabbouj, M.; Inman, D.J. 1D convolutional neural networks and applications: A survey. Mech. Syst. Signal Process. 2021, 151, 107398. [Google Scholar] [CrossRef]
- Eren, L. Bearing Fault Detection by One-Dimensional Convolutional Neural Networks. Math. Probl. Eng. 2017, 2017, 8617315. [Google Scholar] [CrossRef] [Green Version]
- Ince, T.; Kiranyaz, S.; Eren, L.; Askar, M.; Gabbouj, M. Real-Time Motor Fault Detection by 1-D Convolutional Neural Networks. IEEE Trans. Ind. Electron. 2016, 63, 7067–7075. [Google Scholar] [CrossRef]
- Sadouk, L. CNN Approaches for Time Series Classification. In Time Series Analysis—Data, Methods, and Applications; Ngan, C.-K., Ed.; IntechOpen: London, UK, 2019. [Google Scholar] [CrossRef] [Green Version]
- Fawaz, H.I.; Forestier, G.; Weber, J.; Idoumghar, L.; Muller, P.-A. Deep learning for time series classification: A review. Data Min. Knowl. Dis. 2019, 33, 917–963. [Google Scholar] [CrossRef] [Green Version]
- Guttenkunst, E. Study of the Wear Mechanisms for Drill Bits Used in Core Drilling; Uppsala Universitet: Uppsala, Sweden, 2018. [Google Scholar]
- Wang, Z.; Yan, W.; Oates, T. Time Series Classification from Scratch with Deep Neural Networks: A Strong Baseline. arXiv 2016, arXiv:1611.06455. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef] [Green Version]
- Guennec, A.L.; Malinowski, S.; Tavenard, R. Data Augmentation for Time Series Classification Using Convolutional Neural Networks; Halshs-01357973; ECML/PKDD Workshop on Advanced Analytics and Learning on Temporal Data: Riva Del Garda, Italy, 2016. [Google Scholar]
- Zhao, B.; Lu, H.; Chen, S.; Liu, J.; Wu, D. Convolutional neural networks for time series classification. J. Syst. Eng. Electron. JSEE 2017, 28, 162–169. [Google Scholar] [CrossRef]
- Tang, W.; Long, G.; Liu, L.; Zhou, T.; Jiang, J.; Blumenstein, M. Rethinking 1D-CNN for Time Series Classification: A Stronger Baseline. arXiv 2021, arXiv:2002.10061. [Google Scholar]
- Peng, D.; Liu, Z.; Wang, H.; Qin, Y.; Jia, L. A Novel Deeper One-Dimensional CNN with Residual Learning for Fault Diagnosis of Wheelset Bearings in High-Speed Trains. IEEE Access 2019, 7, 10278–10293. [Google Scholar] [CrossRef]
- Ghosh, A.; Sufian, A.; Sultana, F.; Chakrabarti, A.; De, D. Fundamental Concepts of Convolutional Neural Network. In Recent Trends and Advances in Artificial Intelligence and Internet of Things; Balas, V.E., Kumar, R., Srivastava, R., Eds.; Springer International Publishing: Cham, Switzerland, 2020; Volume 172, pp. 519–567. [Google Scholar] [CrossRef]
- Ahmed, W.S.; Karim, A.A.A. The Impact of Filter Size and Number of Filters on Classification Accuracy in CNN. In Proceedings of the 2020 International Conference on Computer Science and Software Engineering (CSASE), Duhok, Iraq, 16–18 April 2020; pp. 88–93. [Google Scholar] [CrossRef]
- Khan, A.; Sohail, A.; Zahoora, U.; Qureshi, A.S. A Survey of the Recent Architectures of Deep Convolutional Neural Networks. Artif. Intell. Rev. 2020, 53, 5455–5516. [Google Scholar] [CrossRef] [Green Version]
- Maaten, L.V.D.; Geoffrey, H. Visualizing Data Using t-SNE. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).