Abstract
Pathfinding algorithms allow for the numerical determination of optimal paths of travel across many applications. These algorithms remain poorly defined for additional consideration of outside parameters, such as fluid flow, while considering contaminant transport problems. We have developed a pathfinding algorithm based on the A* search algorithm which considers the effect of fluid flow behaviors in two dimensions. This search algorithm returns the optimal path between two points in a setting containing impermeable boundaries, allowing for a computational approach to the determination of the most likely path of travel for contaminants or hazards of concern due to fluid flow. This modified A* search algorithm has applications in the statistical modeling of airborne contamination distributions, providing a relative estimate of the statistical relationship between two points in an underground mine’s ventilation system. This method provides a significant improvement to the spatial resolution of minimum-cost path methods currently in use in mine ventilation network software.
1. Introduction
The A* (A-star) search algorithm has an established history as a competent pathfinding algorithm, especially in its ability to return optimal or near-optimal minimum cost paths via a heuristic approach. Since early publications of works involving the A* algorithm and its applications, many versions and derivatives have been developed and successfully implemented in pathfinding and path planning objectives. With the original goal to reduce the space complexity of Dijkstra’s algorithm, the A* algorithm has been repeatedly adopted across multiple disciplines. The most common disciplines to continually utilize the A* search algorithm and its many derivatives are robotics and automation, inspired by the Stanford Research Institute’s Shakey project from 1966 to 1972 [1]. This project aimed to develop an autonomous robot, Shakey, that could navigate around obstacles in a two-dimensional space without collision and in the most efficient manner. With the use of the A* search algorithm informed by visibility graph representations of the space Shakey was designed to traverse, Shakey could move freely around the space while avoiding any obstacles. It was able do so in a manner that while in motion, Shakey would plan and execute a path that considered all possible obstacles at once. This feat was considered a massive advance in path planning for automation, as robots could now move, not only in an entirely automated fashion through any environment but could also do so with near-perfect efficiency [2].
The original A* algorithm is informed by the sum of a cost function and a heuristic function. The cost function traditionally employed by the A* algorithm is the linear distance between a current position and a potential next position. This cost is minimized with smaller step sizes between a current position and a potential position. The heuristic function employed by the A* algorithm is generally some distance function between a potential position and the goal position. The sum of these two functions governs the pathfinding ability of the A* algorithm to return an optimal or near-optimal path between two points. The optimal path occurs where steps between adjacent points move predominantly towards the goal, and where the total number of steps is minimized. The combination of these goals allows the A* algorithm to navigate around boundaries, making it effective in the determination of shortest paths in environments where straight-line travel may not be possible [3].
The cost and heuristic functions that can be employed in the A* search algorithm are not wholly limited to measures of distance. This is evidenced, for example, in applications of wireless sensor network design and optimization in which the cost function is determined by a linear combination of residual and initial energy in the node, number of packets transmitted and received, and the number of free and initial buffers of the node [4]. With changes to the cost or heuristic function in the A* search algorithm, it is possible to tailor the algorithm to serve very specific use cases where high-confidence pathfinding may be necessary [5]. Based on the ability to adjust the A* search algorithm’s cost and heuristic functions, we have developed an additional method for the determination of shortest paths when constrained by the flow of air in closed environments.
On its own, the A* search algorithm has great utility in path planning, even 55 years after Hart, Nilsson, and Raphael’s 1968 paper that first introduced the algorithm to the robotics and automation communities. As evidenced by many adaptations of the A* search algorithm available in the scientific literature, however, the A* algorithm on its own often fails to account for external variables that influence minimum cost paths as outlined in the original 1968 paper. Because of this, it is often necessary to modify components of the A* algorithm to account for these external variables. In 2021, Zhang et al. modified the A* algorithm for unmanned aerial vehicles to include information on network radar systems to construct a dynamic pathfinding algorithm to increase stealth abilities of the vehicles [6]. In 2019, Liu et al. used the A* algorithm as a basis for a new pathfinding algorithm for the planning of ship routes by including considerations for water current, traffic, and maneuverability [7]. Similarly, Zheng, Luo, and Xiao modified the A* algorithm in their 2024 publication, which considered a new heuristic method to reduce unnecessary detours in traditional A* path planning [8]. Marzieh Bagheri et al. developed a modified A* algorithm for the use of cranes in modular construction which considered the cost to lift heavy items in 2020 [9]. In more safety-guided approaches, Veisi et al. developed a modified A* algorithm for path planning after earthquakes that considered the risk of damage to infrastructure in 2023, and Yu, Hou and Chen created a pathfinding algorithm in 2020 based on A* that improved dynamic obstacle avoidance by including that information in the algorithm’s heuristic function [10,11].
Pathfinding algorithms in the mine ventilation network (MVN) software are well established [12]. These algorithms are vital in the assessment of minimum distances between points in the mine, such as distance to a refuge chamber or distance from a known contaminant emitter. At their core, pathfinding algorithms seek to achieve some optimal connection between nodes of a graph [5,13]. These graphs are seen in MVNs and can be used to provide vital insight into the behaviors of air, contaminants, equipment, and individuals. Most vitally, however, is the stipulation that the graph used in MVN software has much lower spatial resolution than that proposed for use here with a modified A* pathfinding algorithm. Graphs in MVN software typically use the mine entry and ventilation ducting as edges of the graph and the intersection of these mine entries and ventilation ducts as vertices. These graphs may be directed and weighted as necessary to reflect in-mine conditions. Ultimately, these graphs have multiple uses, especially in the design of ventilation systems in MVN software which allow for system simulation using the Hardy Cross or similar methods [14,15,16].
A minimum cost pathfinding algorithm for underground mine contaminant transport analysis should be capable of accounting for dynamic and kinematic relationships between the surface roughness of an excavation, mine geometry, and airflow direction. Using current approaches, MVN software can consider these items without issue, albeit with one-dimensional resolution. Because graphs are one-dimensional structures and MVN software relies on a graph realization of the underground space, MVN software is unable to use the existing graph framework to estimate minimum cost paths between locations within mine entries. Instead, minimum cost paths and their corresponding algorithms for MVN software must rely on the relationship between intersections. Ultimately, this poses an issue of resolution for the task at hand. For the large-scale design and planning of ventilation systems, one-dimensional MVN approaches are the logical choice. This begins to break down, however, when considering more granular relationships within the mine and its air. As an example, the spread time metric offered by Ventsim allows for the estimation of the duration required for a contaminant released in one portion of a mine to be detected in another portion of the mine. Because of the one-dimensional nature of MVN approaches, there is no way to determine the spread time at different positions within the same mine entry. This poses a significant barrier to increasing the spatial resolution of estimated contamination distributions within underground ventilation systems.
Outside of an MVN approach, computational fluid dynamics (CFD) approaches have become somewhat popular for questions of contaminant transport in underground mines. In 2020, Huang et al. used CFD to model the transport of carbon monoxide after roadway blasting in underground environments [17]. In 2018, Ren and Wang used CFD modeling to construct realizations of dust and gas flow dispersion across longwall faces in underground coal mines [18]. In 2022, Xie, Xiong, and Chen used CFD to model the movement of gases along roadways of non-metallic mines in an attempt to derive migration laws [19]. The body of work involving CFD for questions of mine ventilation, especially for mining health and safety is expansive. In 2021, Brodny and Tutak compiled a literature review encompassing the use of CFD for underground hard coal mining [20]. It is well known, of course, that CFD methods are incredibly computationally- and time-intensive, even when considering the addition of techniques like machine learning and high-performance computing to accelerate modeling [21,22,23], and while the use of CFD methods allows for increased spatial resolution when compared to MVN methods, they cannot compare to the speeds with which MVN methods can simulate conditions. An intermediate method to begin to assess questions of contamination transport and distribution in underground mines with higher spatial resolution than MVN methods yet faster processing times than CFD methods should be feasible, but there has been very little work conducted in this regard [24].
The modified A* algorithm presented here uses a departure from the typical graph representation of mine ventilation networks used in MVN software. Rather than representing mine entries and ducting as edges and entry intersections as vertices of a directed graph, this modified A* algorithm represents discrete regions within mine entries as vertices. This allows for a higher resolution of data and improved modeling of contaminant transport outside of the typical MVN software or CFD approaches. The development of this modified A* algorithm seeks to create a method for the estimation of spatial relationships between areas in an underground mine for processes that are dependent on the movement of air. This algorithm estimates a possible upper bound for the retained volume of air when moving from an initial location to a target location and prioritizes a path between locations where the retained volume of air is highest. This then represents the most likely path of travel for contaminants through the mine.
This modified pathfinding algorithm is intended to serve as an indicator of relative effective distance between regions within an underground mine’s ventilation system. The outputs of this algorithm have wide-ranging applications, from the determination of the most likely path of travel for contaminants through the mine to the use of the total cost of the path for estimation of contaminant concentration levels using spatial methods like inverse distance weighting or kriging. Work is ongoing that utilizes the modified A* total cost as a substitute distance metric to krige airborne contamination in underground mines, largely inspired by the work of Boisvert and Deutsch (2008) and Boisvert, Manchuk, and Deutsch (2009) wherein Dijkstra’s algorithm was used for kriging in the presence of locally varying anisotropy [25,26]. Rather than returning a shortest path length in terms of a distance, the path length can instead be considered as the sum of costs through the path. This allows for the construction of effective distances on the same relative scale that can then be used for spatial statistics in a manner that can better account for the movement of air without the use of a network representation of the mine ventilation system.
When considering the construction of a minimum cost path in an environment in which fluid flow is the primary agent of movement between points, characteristics of the fluid flow within the space such as flow direction, surface roughness, and pressure losses play a large role. The inclusion of these variables is necessary to produce a minimum cost path with any degree of accuracy. Our method uses a two-dimensional mean flow direction field alongside dynamic and kinematic phenomena to inform the cost function of the search algorithm rather than a traditional, distance-based metric employed in the A* search algorithm as constructed in Hart, Nilsson, and Raphael’s original paper. This allows the pathfinding algorithm to return an optimal path through air within a bounded environment, such as an underground mine, while initially designed for the purpose of pathfinding within an underground coal mine, the modified A* search algorithm can be applied to any environment in which a fluid flow constitutes the primary mechanism of motion. This modified pathfinding algorithm provides a significant improvement in ability to reflect the rank of spread time in underground ventilation systems when compared to the least resistance distance metric available in Ventsim, with the length of path outperforming the least resistance metric in simulations where contamination that does not reach airways are excluded from the rank comparison (p < 0.0005), and the total cost of the path outperforming the metric in simulations where contamination that does not reach airways are included in the rank comparison (p < 0.0005).
2. Materials and Methods
The traditional A* search algorithm comprises two functions, the sum of which is used to determine the fitness of moving from a current position to a neighboring position on the path from some starting point to some ending point. For each set of starting and ending points, the sum of these two functions can be iteratively minimized to return an optimal path of travel. The two functions are referred to as the heuristic function and the cost function [3].
The heuristic function acts as a measure of the distance between a potential neighboring position and the end target, while many potentially admissible heuristic functions exist, the most utilized function is the Manhattan distance function, as shown in Equation (1) [5]. The use of this heuristic is important, as it helps to ensure that the pathfinding algorithm preferentially explores paths that move closer to the goal rather than further away. The heuristic provides an estimate of the minimum possible distance from the starting or current location to the goal location. Other functions, like Euclidean distance, can be used as well, but traversing a fixed grid of points typically requires that search directions remain along the four cardinal directions (up, down, left, right). For this reason, the Manhattan distance function is generally preferred and remains the heuristic function used in the modified algorithm.
where is the Manhattan distance heuristic, calculated as the sum of the absolute difference of the x and y coordinates of the target and neighboring positions. It should be noted that the Manhattan distance heuristic can be likewise adapted to any n-dimensional space, provided that the absolute differences are likewise summed for each corresponding dimension above two-dimensional space.
The A* algorithm is distinguished from Dijkstra’s algorithm by its heuristic function, which reduces space complexity while computing a minimum cost path solution. The use of a distance-based metric enforces a requirement for the A* algorithm to preferentially search for a position that is closer to the target position than the current position . Because of the preferential search, fewer locations must be stored in memory, reducing the space complexity of the algorithm when compared to Dijkstra’s algorithm [3].
The cost function traditionally acts as a measure of the distance between a potential neighboring position and the current position. This function can be recognized as the characteristic function of Dijkstra’s algorithm [13], while Dijkstra’s algorithm is generally applied to the traversal of weighted graphs, the representation of any enclosed space can be likewise represented as a weighted graph of discrete points (vertices) connected by some known or unknown distance between points (weighted edges). When the distances between points are unknown, the graph representation of the space is initially unweighted, and weights must be measured. Weights within a weighted graph may have various representations. The most common weighting in the solution of minimum cost paths for spatial applications is some distance that separates two vertices. As such, for use in the A* algorithm for spatial pathfinding, the Manhattan distance serves as a strong metric to assign weights to the previously unweighted graph. This function holds well where the search directions of the algorithm when selecting potential next steps in the path from the current node to the target node are separated by 90-degree increments, such as up, down, left, and right in 2-dimensional space, or additional directions for forward and backward in 3-dimensional space [5].
The Manhattan distance function serves well as the cost function to calculate edge weights for the A* search algorithm, as in Equation (2).
where is the cost function realized as the Manhattan distance between a neighboring position and a current position.
When the distance between adjacent points within the study space is identical, Equation (2) can be simplified as in Equation (3),
where is the simplified cost function and s is the uniform distance between adjacent, non-diagonal points; while this may reduce the time complexity to return a minimum cost path, the addition of points to create a study space in which points are equally spaced may increase the space complexity required to return the path. To use a simplified cost function, the even spacing of points must be an intrinsic construction of the graph representation of the space prior to implementation of the A* algorithm. Equal spacing allows the cost function of the A* algorithm to perform as a constant value, increasing the speed with which a minimum cost path can be determined. In essence, the assignment of the cost function as a constant value removes distance-based weighting between vertices because the distance between adjacent points is identical. This can be used to simplify the construction of additional weight relationships that determine cost beyond spatial distance because the measurement of distances between adjacent points is no longer necessary.
In doing so, the heuristic function should likewise be normalized as in Equation (4),
where is the simplified heuristic function that has been normalized by dividing by the step size, s. This normalization of the heuristic function ensures that the measure of distance from a candidate position and target position is considered in terms of number of steps between the candidate position and target position, rather than in terms of some original coordinate system prior to simplification of the cost function.
The minimum cost path generated by the A* search algorithm operates as an iterative optimization of the sum of the heuristic and cost functions such that the resulting sum is minimized, as in Equations (5) and (6).
where is the sum of the cost and heuristic values defined by functions and .
This sum is minimized for each location on the path between the start and end points, such that the resulting path can be represented as an ordered set of optimal steps between the start and end points:
where is the set of two-dimensional column vectors or coordinates within the study space that returns the minimum aggregate value of all points p within some set of points along the path.
In application as a computer program, this yields a general approach as in Algorithm 1.
| Algorithm 1 A* Search Algorithm Pseudocode |
|
2.1. Cost Function Determination for Flow-Constrained Paths
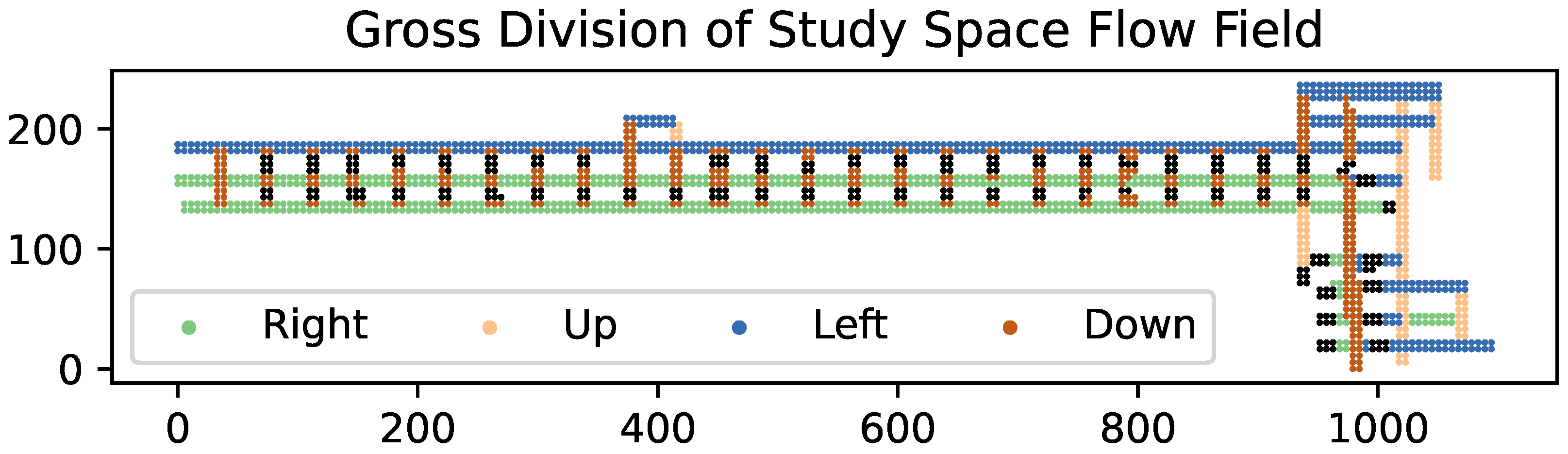
In order to consider minimum cost paths as bound by fluid flow, the flow field must be realized in the same dimensionality as the study space. This field is best displayed as a group of points representing a series of unit vectors indicating direction of fluid flow, as in Figure 1 below. The magnitude of these vectors is irrelevant for the determination of minimum cost paths in this construction of the modified A* algorithm, as direction of flow is assumed to be the primary determinant of the flow path between two locations. Additional consideration of the magnitude of vectors within the flow field is possible for the determination of time of travel and calculations of effective distance between points but provides no meaningful effect on the path of travel, nor is it particularly important to the improved estimation of rank and therefore lies outside the scope of this paper.
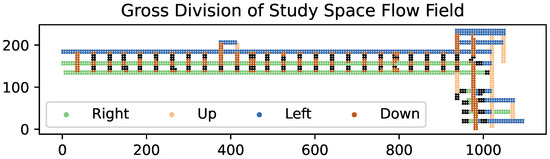
Figure 1.
Gross division of the flow field in the study space. All flow directions are spaced at 90-degree intervals, representing the general trend of fluid flow within the study space. The space pictured is a portion of an underground room-and-pillar coal mine in Emery, UT, USA. Each point represents an approximate area of 15 m2 and the axes indicate transformed mine coordinates in meters.
The modified pathfinding algorithm retains the same heuristic function construction as in the A* search algorithm, as the overall goal of both algorithms is to continually move towards the end target. The cost function, however, is significantly different from the A* search algorithm, as distances between points alone do not provide enough information to inform the algorithm of the fluid flow field. To inform the modified algorithm of the flow field, the cost function is used in a manner similar to Equation (3), where all adjacent, non-diagonal points within the study space are considered equidistant. Using this method, the distance value is some constant and is effectively negligible. Only interactions between movement direction and fluid flow angle need to be considered. Further, the simplified heuristic function in Equation (4) is retained entirely.
By considering the relationship between the angle of fluid flow within the field at the current location as described by the accompanying unit vector and the angle between the current location and neighboring location, the cost function can be constructed as a function of these differences, as in Equations (7) and (8).
where is the criterion angle as defined by the absolute difference between the relative angle of fluid flow, , and the angle of movement (search direction) between the current location and the neighboring location, , when both angles are measured with respect to the positive horizontal axis in a two-dimensional study space.
This criterion angle can be applied to the cost function,
where is the cost function for the modified A* search algorithm dependent on the neighboring position and the criterion angle; and are some small positive values not exceeding 1, tied to volumetric flow reduction due to pressure losses; and s is the step size between adjacent points within the study space. By multiplying the step size by some additional factor, the modified pathfinding algorithm prioritizes motion within 45° of the flow direction over any other movement. Because motion is assumed to be dictated overwhelmingly by fluid flow direction, movement beyond 45 degrees, and especially movement beyond perpendicular to the flow direction is highly penalized to encourage the algorithm’s adherence to the flow field wherever possible.
The motion of contamination, of course, can be perpendicular to or against the direction of general fluid flow and should not be inherently discounted as an allowable movement direction for the algorithm. This movement against or perpendicular to the direction of general fluid flow may arise in regions of the study space where there may be turbulence that can move portions of the fluid body in opposition to the general direction of fluid flow, or in cases where the enclosed study area may branch, allowing some fluid to move into the branched area. In the case of underground coal mining, the movement of air against the direction of general fluid flow can occur when considering friction losses due to surface roughness of shafts, drifts, and crosscuts. The cost function of the modified algorithm seeks to provide an upper bound to the retained volume of air when moving from one location to another, and the total cost of the path should not overestimate the relative spread time from one location to another when comparing the rank of spread time to the rank of total cost.
Right-angle pressure loss, tied to the coefficient in Equation (8), can be generalized across the study space based on the pressure loss due to right-angle movement. This is based on the ratio of curvature radius to hydraulic diameter, , within a section of the study space. A solution for this case is only possible via numerical solutions to the Navier–Stokes equations that require a level of input data pertaining to the boundary and initial conditions that are impractical if not impossible to ascertain across a large, highly variable study space [27,28,29]. As such, several assumptions can be made to estimate an appropriate value of . Primarily, Kirchhoff’s Current Law dictates that all flows into a node must be equal to those leaving a node [14]. In a highly idealized setting in which resistance and geometry are constant, this means that any situation in which flow must move either in line with or perpendicular to general flow direction due to a right-angled branching yields an even division of the original entry flow into two discrete exit flows as per Equation (9).
where and represent the volumetric flows into and out of branches connected by a node, respectively. Volumetric flow can be otherwise generalized according to the square law as a relationship between velocity pressure and resistance per Equation (10) [30].
where P is the frictional pressure loss, and R is the path resistance. Assuming an arbitrary value between 1 and 0.5 yields a pressure loss of approximately 50%. Considering the case requiring movement perpendicular to the direction of general fluid flow, a 50% reduction in velocity pressure with no change in resistance yields a 29.3% reduction in volumetric flow along the perpendicular path as per Equation (11).
The retained fraction of volumetric flow is dependent on the pressure loss encountered. Here, a 50% loss in pressure corresponds to a 70.7% () retention in the section that moves perpendicular to the direction of general fluid flow. Based on Equation (9), the maximum theoretical amount of volumetric flow perpendicular to the direction of general fluid flow is one-half the input flow magnitude. Modified by the 70.7% retention of volumetric flow, this yields a maximum volumetric flow perpendicular to the general flow direction in the form , or approximately 35.4% of the original flow into the node. Based on this number, the coefficient can be estimated as the estimated average fractional pressure drop, , due to right-angle shock loss. Following the structure of Equation (8), yields a movement cost that is inversely proportional to the amount of retained volumetric flow.
Reversed motion in the movement of fluid flow is generally characterized by the thickness of the turbulent boundary layer formed between a region of otherwise more cohesive fluid flow and a solid contact surface [31,32,33]. The thickness of the turbulent boundary layer is highly variable, depending on the Navier–Stokes equations to arrive at a numerical solution or experimentation to reach an experimental result [34,35]. Similarly, the level of input data required severely outweighs any ability to collect said data for use in the modified algorithm. For the purposes of analysis, the coefficient can be estimated as the ratio between the roughness height and the hydraulic diameter, . This is reflected in the cost function for the modified pathfinding algorithm by the ratio of cross-sectional areas defined by , and while this construction of the coefficient () fails to account for numerous other variables that would otherwise be used in solving the boundary layer equations governing reversed flow, it provides an upper limit of reversed volumetric flow because of surface roughness within the study space.
The final cost function for the modified pathfinding algorithm is thereby dependent on the criterion angle, average fractional pressure loss due to perpendicular motion, and the surface roughness as a ratio of roughness height to the hydraulic diameter. This yields a cost function as shown in Equation (12).
With further implementation, values for and can be included in the algorithm inputs directly, albeit with increased time complexity. An average value for may be estimated via network simulation in a ventilation simulation software or via computational fluid dynamics, and can likewise be estimated via methods outlined in Watson and Marshall’s 2015 paper discussing methods for determining absolute surface roughness, e [36]. Estimation of shock loss can be computed using CFD methods, as described by Zhang, Falk, and Allen (2024), or derived numerically as described by Levin and Semin (2019) [37,38]. More modern approaches to the estimation of surface roughness have similarly included the use of photogrammetry and point clouds, as outlined in Li et al. (2023) and Gao et al. (2022) [39,40]. For the sake of analysis in this paper, we have elected a value of 0.5 for and a value of 0.025 for . These values represent a rather typical shock loss through a 90-degree turn between two identically sized cross sections as would be encountered in an underground mine, and a reasonable expectation of surface roughness during well-controlled blasting or excavation during the mining process. These values are easily obtained from values listed in Chapter 5 of McPherson’s Subsurface Ventilation and Environmental Engineering for shock loss, and the United States Bureau of Mines friction factor tables or McPherson’s Subsurface Ventilation and Environmental Engineering to estimate absolute roughness via the Von Kármán Equation [30,41]. As estimated values, and have been chosen in a manner that likely understates the effect on volumetric loss when moving between two points. This understatement is important for the sake of admissibility. Admissibility seeks to ensure that any more efficient paths are not excluded from consideration while solving a minimum cost path problem [5].
This admissibility feature is a requirement for the successful implementation of pathfinding algorithms [42]. To ensure an optimal or near-optimal path is found, the cost and heuristic functions must return values that do not overestimate the true cost along the most optimal path. The cost function as implemented in the modified pathfinding algorithm is inversely proportional to the change in volume between two points. This change in volume cannot overestimate the true change in retained volume observed in the space. To ensure an admissible cost function, the values selected for and are optimistic. These values yield an overestimation of the volume change, which underestimates the cost to move between two points. This leads to an optimized path between two points. Because of this admissibility requirement, the equations bridging the two notations of the cost function as presented in Equations (8) and (12) do not seek to perfectly estimate the behavior of fluid flow by considering all factors that impact the movement of fluids. If that were the case, a computational fluid dynamics approach that uses the Navier–Stokes equations would be overwhelmingly more favorable. Instead, these equations attempt to provide a simple means for predicting behavior on a scale that is intermediate to MVN and CFD methods without the intense computational load associated with CFD. This behavior can likewise be validated using MVN software to assess that the modified A* algorithm is generally capable of making these estimations.
2.2. Validation of the Modified A* Algorithm
Because the modified pathfinding algorithm returns shortest paths with respect to airflow direction, numerous applications of the algorithm are feasible. By considering the calculated cost between discrete locations in a mine’s ventilation system, the modified A* algorithm can estimate the shortest possible path of travel of a contaminant in an underground mining environment without the use of a network solver typical of MVN software. With the coal of using the total path cost calculated by the modified A* algorithm as an indicator of the statistical relationship between two points in a mine’s ventilation system, spread time can be used as a helpful MVN-based starting point from which to measure the performance of the modified algorithm.
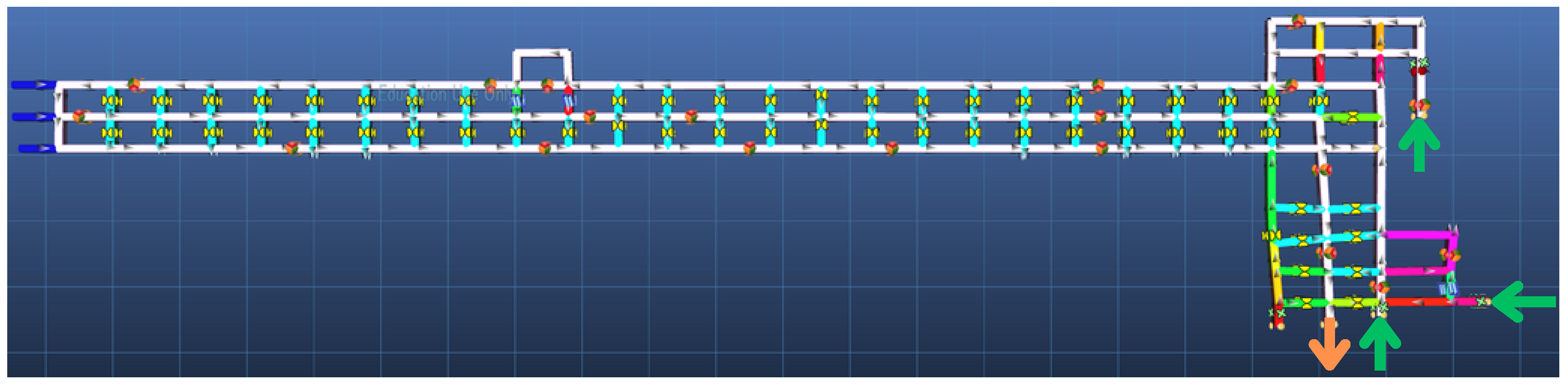
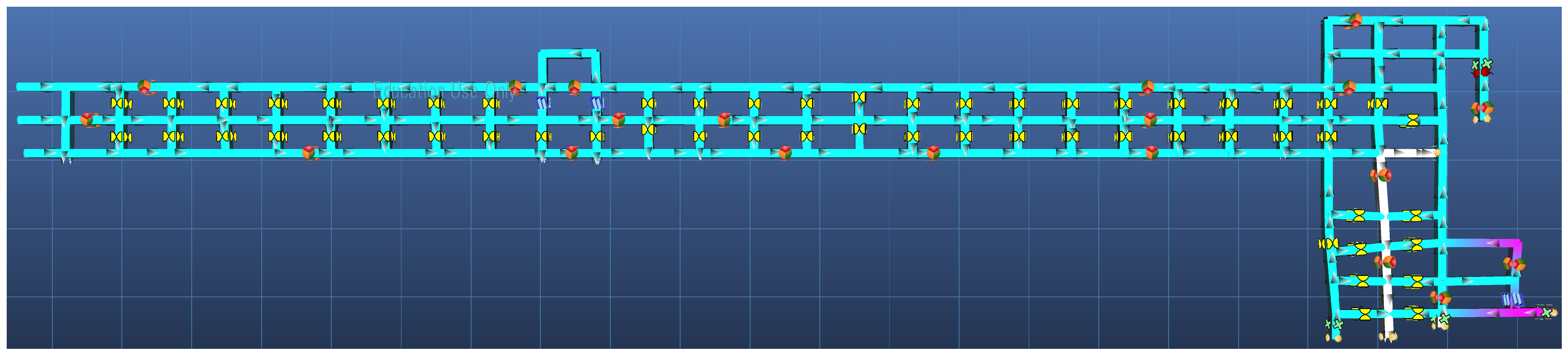
Using Ventsim 5.4, a section of the underground mine can be constructed as in Figure 2. The section has two intakes with volumetric flow rates of 19 m3/s, indicated with the upwards green arrows in the figure, and an additional intake with a volumetric flow rate of 6 m3/s to provide a minimum air velocity of 0.3 m/s throughout the entire section. Air is exhausted from one major outlet indicated in the figure, with an additional minor outlet from the section via an overpass not indicated in the figure for the sake of visual clarity. The simulation of a steady-state contaminant release at 100 ppm in the mining environment can return a set of spread times calculated by Ventsim.
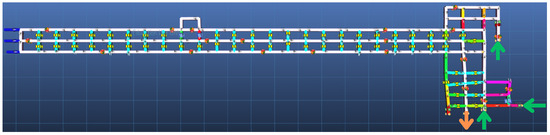
Figure 2.
MVN representation of underground mine section in Ventsim 5.4. Section intakes are indicated with green arrows and exhaust with an orange arrow.
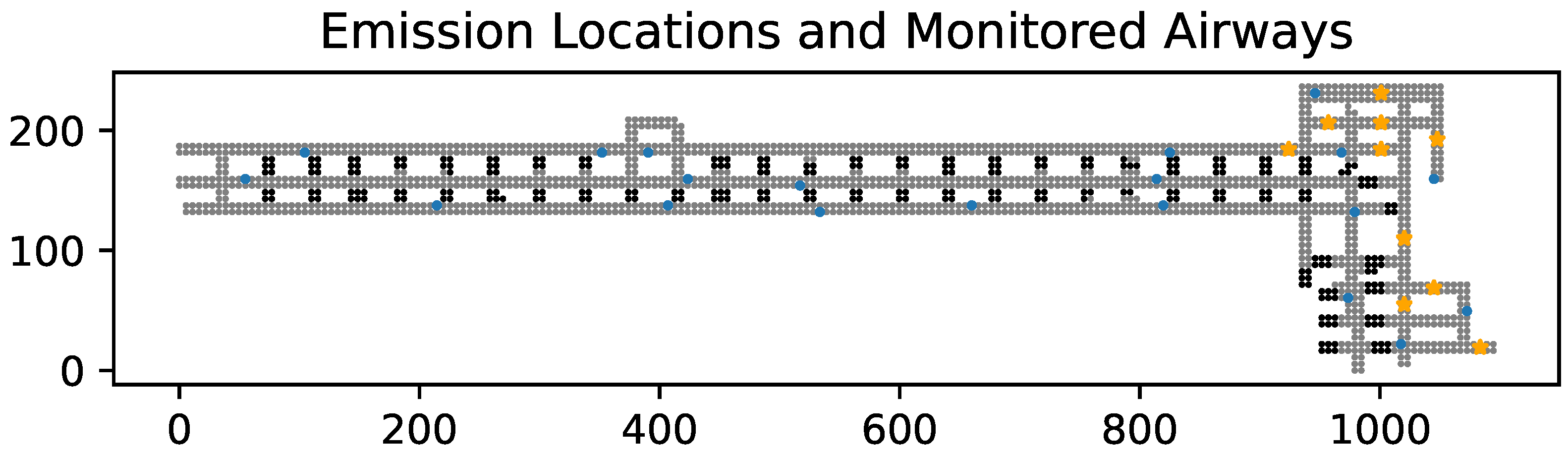
To verify the pathfinding algorithm, results of the modified A* pathfinding algorithm can be used to estimate the order in which contamination would reach the airway, while this estimation is possible in Ventsim and similar MVN software, estimation of spread time requires a network representation of the ventilation system. With the use of a pathfinding algorithm, the modified A* algorithm stands to remove the need for a network representation of the system while improving spatial resolution of the space. This method still relies on a graph representation of the space, but by representing discrete regions of the ventilation system as nodes rather than mine entries as branches. In other words, the space can be represented as a bidirected graph where each node represents a point in the ventilation system rather than an intersection of airways. As a result, the modified A* algorithm will be able to predict behavior within mine entries, which is not otherwise feasible in Ventsim. By varying the placement of contaminant sources in Ventsim 5.4, multiple observations of path of travel are possible. The selected locations are indicated in Figure 3, with airways containing emitters marked in orange. Only one location contains the contamination source at a time, for a total of ten scenarios. A set of 20 airways were selected for analysis, with care taken to distribute the monitored airways somewhat evenly within the space. Because the modeled portion of the underground coal mine is composed of 182 discrete airways, an analysis of 10% of the airways in the simulation provides a large enough sample to generalize the behavior across the portion of the mine. When combining this with ten locations for emitters, this represents approximately 15% of the portion of the mine that is considered in-depth in analysis. The selected airways are likewise indicated in Figure 3. By comparing the least resistance path calculated by Ventsim and the modified A* pathfinding algorithm’s total cost and path length with the calculated spread time generated by the network solver, the two pathfinding methods can be used to gauge their fitness as a surrogate for spread time.
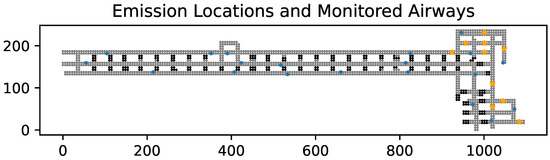
Figure 3.
Locations of contaminant sources during simulation in Ventsim (orange) and airways monitored for spread time analysis (blue).
To judge the fitness of the pathfinding algorithm, pathfinding cost results can be ranked and compared to the rank of spread time. A pathfinding method serving as a perfect surrogate for spread time would return costs whose rank match the rank of spread time for all airways. For building a statistical relationship between locations in the mine’s ventilation system, an acceptable metric from the modified A* algorithm should provide a rank that matches or underestimates the rank of spread time while providing higher spatial resolution and improved accuracy than other minimum-cost pathfinding methods currently available in MVN software. To assess the performance of the modified A* algorithm, the ranks of path length and total cost can be compared to the least resistance measurement in Ventsim as a surrogate for spread time. Naturally, the flow of airborne contamination should follow a path of least resistance, providing some relation to spread time that could potentially be used to krige airborne contamination distributions, but the adoption of the modified A* algorithm’s path length or total cost should ideally outperform the least resistance metric.
3. Results and Discussion
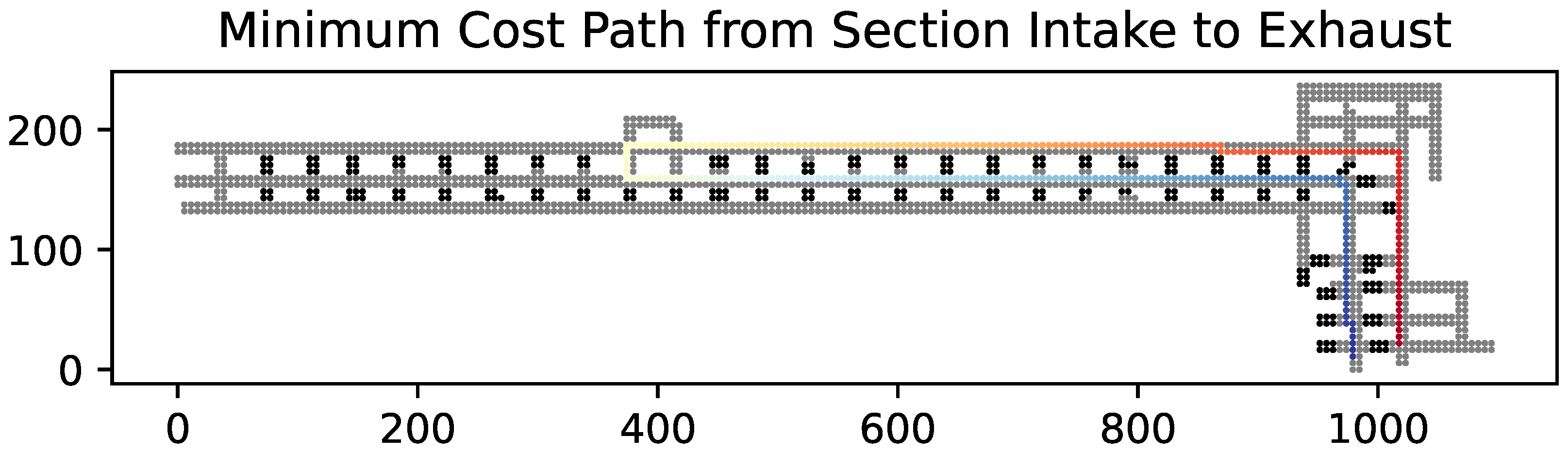
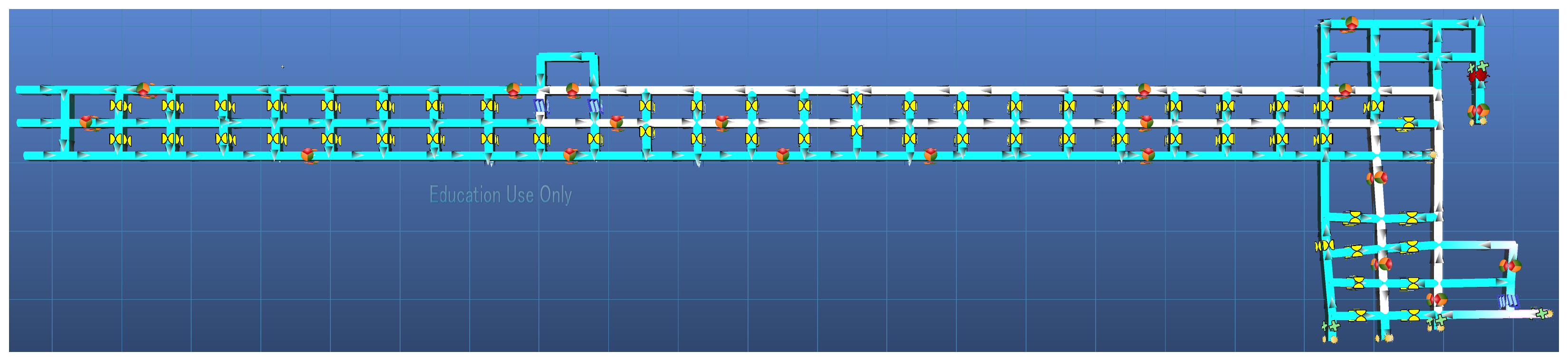
Qualitatively, the modified A* algorithm performs as expected, returning a path between two locations within the mine that follows the direction of airflow. Figure 4 indicates the minimum-cost modified A* path between one of the section’s intakes and the section’s exhaust. Comparing this with the least resistance path as measured in Ventsim (Figure 5), this shows strong agreement with an MVN approach.
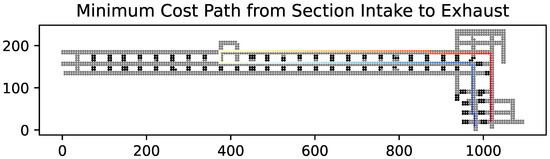
Figure 4.
Minimum cost path from one of the section’s intakes to its exhaust. The path starts indicated in red and ends in blue.
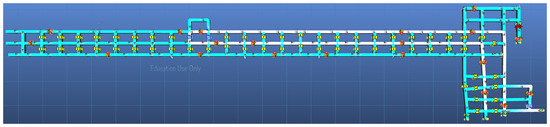
Figure 5.
Least resistance path as calculated by Ventsim. Note that the paths returned are identical in terms of airways used.
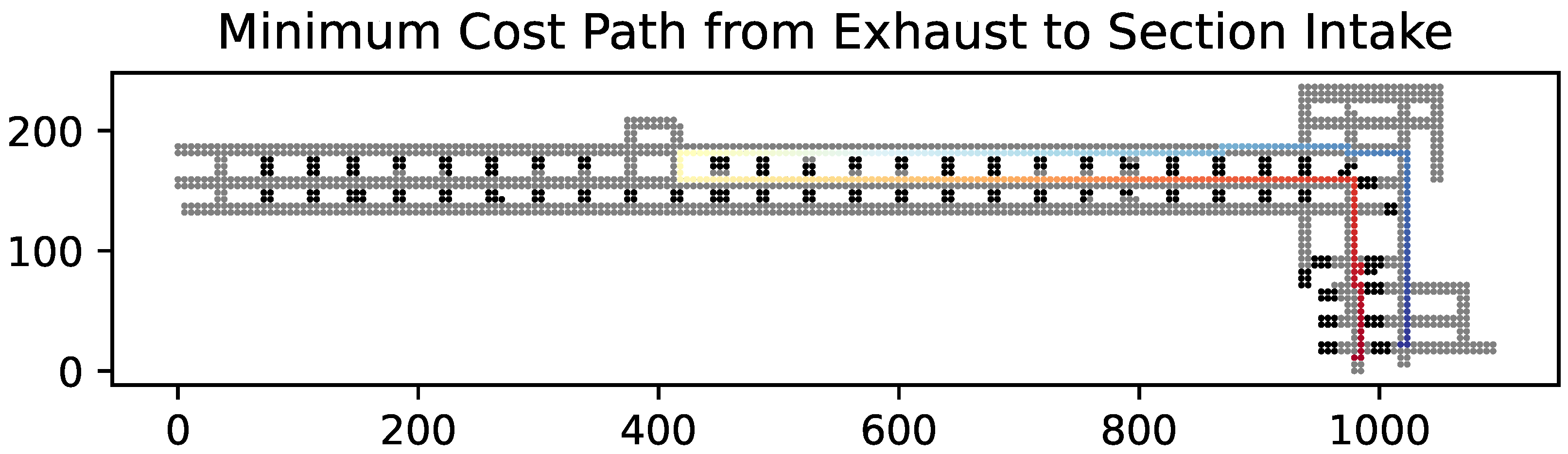
Most notably, the modified A* algorithm can return a minimum cost path in the reverse direction (Figure 6) as well, which Ventsim is not always capable of. This is a consequence of representing the space as a network. Naturally, it would not be appropriate to assume that the shortest path of contaminant travel between two points in this reverse case would be to exit the section entirely and re-enter, as suggested by Ventsim in Figure 7. This limitation of MVN approaches is especially visible in this case, where only a portion of the ventilation system is modeled in Ventsim. For the eventual use case in the kriging of air contamination distributions, it is vital to construct measures of statistical relation that reflect the anisotropic nature of a mine’s ventilation system. In this reverse case, it is clearly much more likely that contamination could reach a location despite adverse flow conditions because of mixing and reversal within the turbulent boundary layer at the ribs, back, and floor of the excavation than considering the complete exhausting of the contaminant and re-entry of the still-entrained contaminant in the section supply. As such, any metric that is to be used to measure the statistical relation between points in the mine’s ventilation system should return paths that are entirely constrained to the ventilation system, without assuming exhausted contamination will remain entrained in intake air; while this is not a possibility for MVN software like Ventsim, the modified A* algorithm is capable of enforcing this requirement.
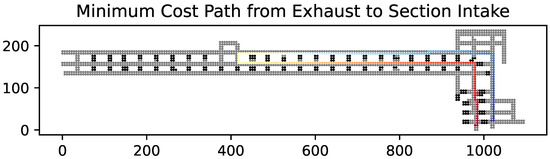
Figure 6.
Minimum cost path from the section’s exhaust to one of its intakes. The path starts indicated in red and ends in blue. Note that the path has changes slightly but remains entirely constrained to the section of the mine.
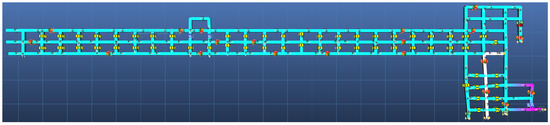
Figure 7.
Least resistance path as calculated by Ventsim from the section’s exhaust to one of its intakes. Note the nonsensical route suggested by the software due to the use of an MVN approach.
The modified A* algorithm was compared to the least resistance metric within Ventsim to assess the appropriateness of the algorithm for use as a surrogate for spread time that improves the spatial resolution. Spread time, as calculated in Ventsim, cannot account for conditions under which contamination is unlikely to reach an entry. Within Ventsim, the spread time is indicated as 99,999 when this occurs. Two sets of t-tests can be performed to determine whether the modified A* algorithm path length or total cost values outperform the least resistance measurement.
First, the cases where spread time in an entry is reported at 99,999 can be excluded from analysis. This has various implications, especially as it pertains to capturing short-scale and long-scale statistical relationships. By excluding values of 99,999 from analysis, the reverse cases that Ventsim cannot address as discussed above are ignored. Spread times, path lengths, total costs, and least resistance path lengths can all be ranked, and a success rate can be determines as the percentage of observations for which the ranks of various surrogate metrics do not overestimate the rank of spread time. Table 1 displays the success rates of these various surrogate metrics when spread time values of 99,999 are excluded.

Table 1.
Success rates for various surrogate metrics with spread time = 99,999 excluded from analysis.
The total path length as computed using the modified A* algorithm significantly outperforms the last resistance metric in Ventsim (p < 0.0005), and the total cost likewise provides an improvement over the least resistance metric, albeit with a slightly higher p-value (p < 0.001). By extension, when excluding spread times of 99,999, the path length from the modified A* algorithm significantly outperforms the total cost (p < 0.005), but less drastically than improvements seen over the least resistance measurements.
Alternatively, spread times of 99,999 can be included in analysis. This inclusion can provide an insight into the modified A* algorithm’s ability to handle these reverse cases as mentioned above. Obviously, success rates should be lower than when values of 99,999 are excluded from analysis, but their inclusion can highlight the dramatic improvement over using the least resistance measurement in Ventsim as a method for determining statistical relationships between locations in underground ventilation systems. Table 2 displays the success rates for least resistance measurements, total path cost, and the modified A* path length when values of 99,999 are included in the analysis.

Table 2.
Success rates for various surrogate metrics with spread time = 99,999 included in analysis.
Here, the total cost of the modified A* algorithm’s returned path dramatically outperforms the least resistance metric with p < 0.0005. Interestingly, the modified A* algorithm’s path length significantly under-performs when compared to the least resistance measurement in Ventsim (p < 0.01). By extension, the total cost provides a significant improvement (p < 0.000005) in success rate over the path length when spread times of 99,999 are considered.
For the use as a potential distance metric for the statistical estimation of airborne contamination distributions, the modified A* algorithm’s total cost of path is a very promising candidate. Without the need for a graph representation like those used in MVN approaches, this distance metric can be used to provide a much higher spatial resolution than otherwise available. Additionally, compared to a least resistance metric that is possible to calculate in MVN software, the modified A* algorithm’s total cost significantly outperforms any other method to reflect relative statistical relationships more accurately between points in the mine. The modified A* algorithm shows superior adherence to spread time, which is ultimately one of the best currently available ways of gleaning information pertaining to the path of travel of airborne contamination in underground mines. Because the modified A* method can use a significantly smaller cell size than the entire-entry representation of the mine’s ventilation system, distribution estimation using statistical method could stand to have much improved spatial resolution while retaining model accuracy. Preliminary, in silico assessment of the use of the modified A* method’s total cost of path for ordinary kriging of airborne contamination distributions has shown promising results, with further testing planned.
Naturally, testing the modified A* algorithm against a MVN realization of a mine’s ventilation system will only serve to validate large-scale behaviors of the algorithm. Just as MVN approaches are limited in their ability to consider behaviors within different parts of the same airway, this analysis is limited to behaviors between airways. Notably, the above results continue to hold when the monitored locations as indicated in Figure 3 are moved to any other place within the same airway. Regardless, further analysis with a method capable of providing improved spatial resolution may be worthwhile, but care should be taken when using methods like computational fluid dynamics or fast fluid dynamics, as the determination of initial and boundary conditions as well as simplifications to the model for the sake of processing time can have an outsized impact on actual behaviors within the mine entry [43,44,45]. Ultimately, this harms the reliability of the use of the CFD method for analysis and can be evident when comparing CFD results with experimental data. Additionally, computational fluid dynamics, including fast fluid dynamics methods are incredibly computationally intensive; it may not be possible to accurately model a portion of the mine large enough to perform any adequate analysis while using a grid size that is small enough to avoid grid dependency [46]. As such, we suggest that further validation of this method would be best achieved using tracer gases in actual underground mines, or via post hoc analysis of model and algorithm performance when using the modified A* algorithm in the estimation of contamination distributions in actual underground mines.
The modified A* algorithm, as presented, is still limited in its ability to construct meaningful relationships with the same resolution as computational fluid dynamics methods and is especially limited by its nature as a two-dimensional method. Additional work is required to assess the function of the modified A* algorithm as a three- or n-dimensional method. Any future work seeking to expand the modified A* algorithm’s capabilities by considering cases in three dimensions should take great care to assess the feasibility of determining the general three-dimensional behavior of airflow within the ventilation system. Additionally, while the “pure” A* algorithm (and by extension, the modified A* algorithm) does provide a significant reduction in space complexity when compared to Dijkstra’s algorithm, time and space complexities for the modified A* algorithm should reasonably be expected to worsen with each additional search direction added to the space. In the two-dimensional case presented, there is a maximum of four cardinal directions the algorithm must consider when identifying the minimum cost path. For a three-dimensional case, this would be a maximum of six cardinal directions, with each additional dimension adding two cardinal directions to the maximum number of directions the algorithm must consider.
4. Conclusions
This modified A* algorithm seeks to describe minimum cost paths based on a fluid flow field within a two-dimensional study space of any arbitrary geometry that can be realized as a continuous space consisting of a single region. As an extension of the A* search algorithm, the modified algorithm provides a reliable estimation of the shortest path between points with respect to additional dynamic and kinematic factors that the traditional A* algorithm cannot directly account for by including information on the direction of airflow. Despite the obvious exclusion of other endogenous factors that impact the transport of contamination, this pared-down model continues to provide a suitable means of estimating path-of-travel of contamination in underground mines. This behavior is verified in Ventsim by comparing the spread time to the total cost of the path. The modified A* algorithm consistently outperforms other pathfinding methods available in Ventsim, especially the least resistance measurement, which should theoretically provide similar performance. This method proves promising in its ability to estimate paths of travel for airborne contamination. Its superiority to other pathfinding methods in MVN software, both in accuracy and spatial resolution, suggest that the total cost of path as calculated by the modified A* algorithm could function well as a measure of statistical relation between discrete locations within underground ventilation systems.
While more work is indicated in the validation of short-scale behaviors and the implementation of the modified algorithm in three- and n-dimensional cases, the initial validation presented shows the promising nature of the modified A* algorithm. To proceed with spatial interpolation in a highly anisotropic space, the determination of statistical relationships within a mine’s ventilation system is crucial to model performance; while other distance metrics, like the least resistance measurement in Ventsim, are available for use with MVN representations of ventilation systems, they are inherently limited by the one-dimensional nature of MVN representations. This modified pathfinding algorithm presents an opportunity to increase spatial resolution of contamination distribution and transport models by taking a step away from the traditional graph representation of underground ventilation systems. As discussed above, future work should focus on the validation of this pathfinding algorithm through experimental means; while the initial results via simulation are promising, the use of tracer gases and real-time gas monitoring would allow for an additional layer of validation to show that the algorithm functions as intended. Additionally, verification through simulation using more expansive underground ventilation models and models for other underground mines will help to evaluate the robustness of this approach.
The A* algorithm and similar pathfinding algorithms are incredibly applicable to questions in engineering and science, as highlighted by the explosion of derivative pathfinding methods presented in the past several decades [6,7,8,9,10,11]. With the modifications to the original A* algorithm we have presented, this modified algorithm can begin to account for the effects of airflow direction and excavation roughness as a means of determining the path of travel of contamination in underground ventilation systems. This is highly applicable for future work to estimate contamination distributions without the use of computational fluid dynamics or mine ventilation network methods, which can stand to provide estimates with less time and space complexity than CFD method by higher spatial resolution than MVN methods. By using the modified A* algorithm as a measure of statistical relation between locations in a mine’s ventilation system, these models could stand to better account for locally varying anisotropy in the ventilation system. At current, the other alternative would be to use Euclidean distances, which would be wholly incapable of accounting for this anisotropy. Large-scale validation in Ventsim 5.4 shows a stronger correlation between spread time and the modified A* algorithm’s total cost of path than Ventsim’s least resistance pathfinding distance, further showing the capabilities of the A* algorithm and its derivatives, especially when considering the impact of factors that guide physical phenomena.
Author Contributions
Conceptualization, K.B.R.; methodology, K.B.R.; software, K.B.R.; validation, K.B.R. and M.M.; data curation, K.B.R.; writing—original draft preparation, K.B.R.; writing—review and editing, K.B.R. and M.M.; visualization, K.B.R.; supervision, M.M.; funding acquisition, M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Institute of Occupational Safety and Health (NIOSH) under award number U60OH012351.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
The mine geometry utilized in this publication was provided by Bronco Utah Operations, LLC’s Emery underground coal mine in Emery, UT, USA. We would like to give special thanks to the Emery mine and its health and safety and tech services teams for continuing access to their data.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kuipers, B.; Feigenbaum, E.A.; Hart, P.E.; Nilsson, N.J. Shakey: From conception to history. AI Mag. 2017, 38, 88–103. [Google Scholar] [CrossRef]
- Lozano-Pérez, T.; Wesley, M.A. An algorithm for planning collision-free paths among polyhedral obstacles. Commun. ACM 1979, 22, 560–570. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Ghaffari, A. An energy efficient routing protocol for wireless sensor networks using A-star algorithm. J. Appl. Res. Technol. 2014, 12, 815–822. [Google Scholar] [CrossRef]
- Nosrati, M.; Karimi, R.; Hasanvand, H.A. Investigation of the *(star) search algorithms: Characteristics, method and approaches. World Appl. Program. 2012, 2, 251–256. [Google Scholar]
- Zhang, Z.; Wu, J.; Dai, J.; He, C. Optimal path planning with modified A-Star algorithm for stealth unmanned aerial vehicles in 3D network radar environment. Proc. Inst. Mechancial Eng. Part G J. Aerosp. Eng. 2022, 236, 72–81. [Google Scholar] [CrossRef]
- Liu, C.; Mao, Q.; Chu, X.; Xie, S. An Improved A-Star Algorithm Considering Water Current, Traffic Separation and Berthing for Vessel Path Planning. Appl. Sci. 2019, 9, 1057. [Google Scholar] [CrossRef]
- Zheng, S.; Luo, L.; Xiao, Y. Global Path Planning for USV Using A-Star Algorithm with Modified Heuristic Function. In Proceedings of the 2024 IEEE 4th International Conference on Power, Eelctronics and Computer Applications (ICPECA), Shenyang, China, 26–28 January 2024. [Google Scholar] [CrossRef]
- Marzieh Bagheri, S.; Taghaddos, H.; Mousaie, A.; Shahnavaz, F.; Hermann, U. An A-Star algorithm for semi-optimization of crane location and configuration in modular construction. Autom. Constr. 2020, 121, 103447. [Google Scholar] [CrossRef]
- Veisei, O.; Du, D.; Moradi, M.A.; Guasselli, F.G.; Athanasoulias, S.; Syed, H.A.; Müller, C.; Stevens, G. Desiging SafeMap Based on City Infrastructure and Empirical Approach: Modified A-star Algorithm for Earthquake Navigation Application. In Proceedings of the 1st ACM SIGSPATIAL International Workshop on Advances in Urban-AI, Hamburg, Germany, 13 November 2023; pp. 61–70. [Google Scholar] [CrossRef]
- Yu, J.; Hou, J.; Chen, G. Improved Safety-First A-Star Algorithm for Autonomous Vehicles. In Proceedings of the 5th International Conference on Advanced Robotics and Mechatronics (ICARM), Shenzhen, China, 18–21 December 2020. [Google Scholar] [CrossRef]
- Stewart, C.; Aminossadati, S.M.; Kizil, M.S. Emergency egress pathway prediction using ventilaiton models. In Proceedings of the 4th Austrialian Mine Ventilation Conference, Brisbane, Australia, 28–30 August 2017; pp. 57–62. [Google Scholar]
- Dijkstra, E.W. A note on two problems in connexion with graphs. In Edsger Wybe Dijkstra: His Life, Work, and Legacy; Apt, K.R., Hoare, T., Eds.; Morgan & Claypool: San Raphael, CA, USA, 2022; pp. 287–290. [Google Scholar]
- McPherson, M.J. Ventilation network analysis. In Subsurface Ventilation and Environmental Engineering; Springer: New York, NY, USA, 1993; pp. 209–240. [Google Scholar]
- Wei, L.J. Topology theory of mine ventilation network. Procedia Earth Planet. Sci. 2009, 1, 354–360. [Google Scholar] [CrossRef]
- Jha, A.K. Ventilation Network Analysis. In Selection of Main Mechanical Ventilators for Coal Mines; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Huang, R.; Shen, X.; Wang, B.; Liao, X. Migration characteristics of CO under forced ventilation after excavation roadway blasting: A case study in a plateau mine. J. Clean. Prod. 2020, 267, 122094. [Google Scholar] [CrossRef]
- Ren, T.; Wang, Z. CFD Modelling of Ventilation, Dust and Gas Flow Dispersion Patterns on a Longwall Face. In Proceedings of the 11th International Mine Ventilation Congress, Xi’an, China, 14–20 September 2018; pp. 198–208. [Google Scholar] [CrossRef]
- Xie, C.; Xiong, G.; Chen, Z. Using CFD to Simulate Concentration of Polluting and Harmful Gases in the Roadway of Non-Metallic Mines Reveals Its Migration Law. Sustainability 2022, 14, 13349. [Google Scholar] [CrossRef]
- Brodny, J.; Tutak, M. Applying computational fluid dynamics in research on ventilation safety during underground hard coal mining: A systematic literature review. Process Saf. Environ. Prot. 2021, 151, 373–400. [Google Scholar] [CrossRef]
- Kavuri, C.; Kokjohn, S.L. Exploring the potential of machine learning in reducing the computational time/expense and improving the reliability of engine optimization studies. Int. J. Engine Res. 2020, 21, 1251–1270. [Google Scholar] [CrossRef]
- Mirzaei, P. CFD modeling of micro and urban climates: Problems to be solved in the new decade. Sustain. Cities Soc. 2021, 69, 102839. [Google Scholar] [CrossRef]
- Lange, C.; Barthelmäs, P.; Rosnitschek, T.; Tremmel, S.; Rieg, F. Impact of HPC and Automated CFD Simulation Processes on Virtual Product Development—A Case Study. Appl. Sci. 2021, 11, 6552. [Google Scholar] [CrossRef]
- Brown Requist, K.W.; Lutz, E.; Momayez, M. Near real-time interpolative algorithm for modelling air quality in underground mines. J. South. Afr. Inst. Min. Metall. 2024, 124, 153–162. [Google Scholar]
- Boisvert, J.B.; Deutsch, C.V. Kriging in the Presence of LVA Using Dijkstra’s Algorithm. 2008. Available online: https://www.ccgalberta.com/ccgresources/report10/2008-110_lva_kriging_dijkstra.pdf (accessed on 24 April 2024).
- Boisvert, J.B.; Manchuk, J.G.; Deutsch, C.V. Kriging in the Presence of Locally Varying Anisotropy Using Non-Euclidean Distances. Math. Geosci. 2009, 41, 585–601. [Google Scholar]
- Umeda, S.; Yang, W.J. Interaction of von Karman vortices and intersecting main streams in staggered tube bundles. Exp. Fluids 1999, 26, 389–396. [Google Scholar] [CrossRef]
- Karode, S.K.; Kumar, A. Flow visualization through spacer filled channels by computational fluid dynamics I: Pressure drop and shear rate calculations for flat sheet geometry. J. Membr. Sci. 2001, 193, 90–95. [Google Scholar] [CrossRef]
- Prasad, R.K. Pressure transient analysis in the presence of two intersecting boundaries. J. Pet. Technol. 1975, 27, 89–96. [Google Scholar] [CrossRef]
- McPherson, M.J. Incompressible flow relationships. 1993. In Subsurface Ventilation and Environmental Engineering; Springer: New York, NY, USA, 1993; pp. 134–174. [Google Scholar]
- Andreopoulos, J.; Wood, D. The response of a turbulent boundary layer to a short length of surface roughness. J. Fluid Mech. 1982, 118, 143–164. [Google Scholar] [CrossRef]
- Krogstadt, P.Å.; Antonia, R.A. Surface roughness effects in turbulent boundary layers. Exp. Fluids 1999, 27, 450–460. [Google Scholar] [CrossRef]
- Tuck, E.; Kouzoubov, A. A laminar roughness boundary condition. J. Fluid Mech. 1995, 300, 59–70. [Google Scholar] [CrossRef]
- Antonia, R.A.; Luxton, R.E. The response of a turbulent boundary layer to a step change in surface roughness. Part 2. Rough-to-smooth. J. Fluid Mech. 1972, 53, 737–757. [Google Scholar] [CrossRef]
- Raupach, M.R. Conditional statistics of Reynolds stress in rough-wall and smooth-wall turburlent boundary layers. J. Fluid Mech. 1981, 108, 363–382. [Google Scholar] [CrossRef]
- Watson, C.; Marshall, J.A. Towards Extracting Absolute Roughness from Underground Mine Drift Profile Data. 2015. Available online: https://qspace.library.queensu.ca/handle/1974/14116 (accessed on 22 June 2023).
- Zhang, H.; Falk, L.; Allen, C. An Application of Computational Fluid Dynamics to Predict Schock Loss Factors at Raise Junctions in Underground Mine Ventilation Systems. Min. Metall. Explor. 2024, 41, 1155–1170. [Google Scholar] [CrossRef]
- Levin, L.Y.; Semin, M.A. Influence of Schock Losses on Air Distribution in Underground Mines. J. Min. Sci. 2019, 55, 287–296. [Google Scholar] [CrossRef]
- Li, K.; Ramandi, H.L.; Zhang, C.; Saydam, S.; Oh, J.; Saydam, S. Exploring the capabilities of portable device photogrammetry for 3D surface roughness evaluation. Int. J. Min. Reclam. Environ. 2023, 37, 630–647. [Google Scholar] [CrossRef]
- Gao, K.; Qi, Z.; Liu, Y.; Zhang, J. Calculation model for ventilation friction resistance coefficient by surrounding rock roughness distribution characteristics of mine tunnel. Sci. Rep. 2022, 12, 3193. [Google Scholar] [CrossRef]
- McElroy, G.E. Engineering Factors in the Ventilation of Metal Mines; US Government Printing Office: Washington, DC, USA, 1935; p. 43. [Google Scholar]
- Korf, R.E. Recent progress in the design and analysis of admissible heuristic functions. In Proceedings of the Abstraction, Reformulation, and Approximation: 4th International Symposium, SARA 2000, Horseshoe Bay, TX, USA, 26–29 July 2000; pp. 45–55. [Google Scholar]
- Yuan, L.; Zhou, L.; Smith, A.C. Modeling carbon monoxide spread in underground mine fires. Appl. Therm. Eng. 2016, 100, 1319–1326. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Goodman, G.; Martikainen, A. Computational fluid dynamics (CFD) investigation of impacts of an obstruction on airflow in underground mines. Trans. Soc. Min. Met. Explor. Inc. 2013, 332, 505–513. [Google Scholar] [PubMed]
- Chang, P.; Xu, G.; Huang, J. Numerical study on DPM dispersion and distribution in an underground development face based on dynamic mesh. Int. J. Min. Sci. Technol. 2020, 30, 471–475. [Google Scholar] [CrossRef]
- Mora, L.; Gadgil, A.J.; Wurtz, E.; Inard, C. Comparing Zonal and CFD Model Predictions of Indoor Airflows under Mixed Convection Conditions to Experimental Data. In Proceedings of the 3rd European Conference on Energy Performance and Indoor Climate in Buildings, Lyon, France, 23–26 October 2002. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).