TLS in Sustainable Mining Engineering: 3D Convergence and Surface Changes in Chamber Excavation in CH Salt Mine “Wieliczka”
Abstract
1. Introduction
2. Traditional Convergence Measurement Methods
- dV′ is the excavation volume after deformation, and
- dV is the initial excavation volume.
3. Materials and Methods
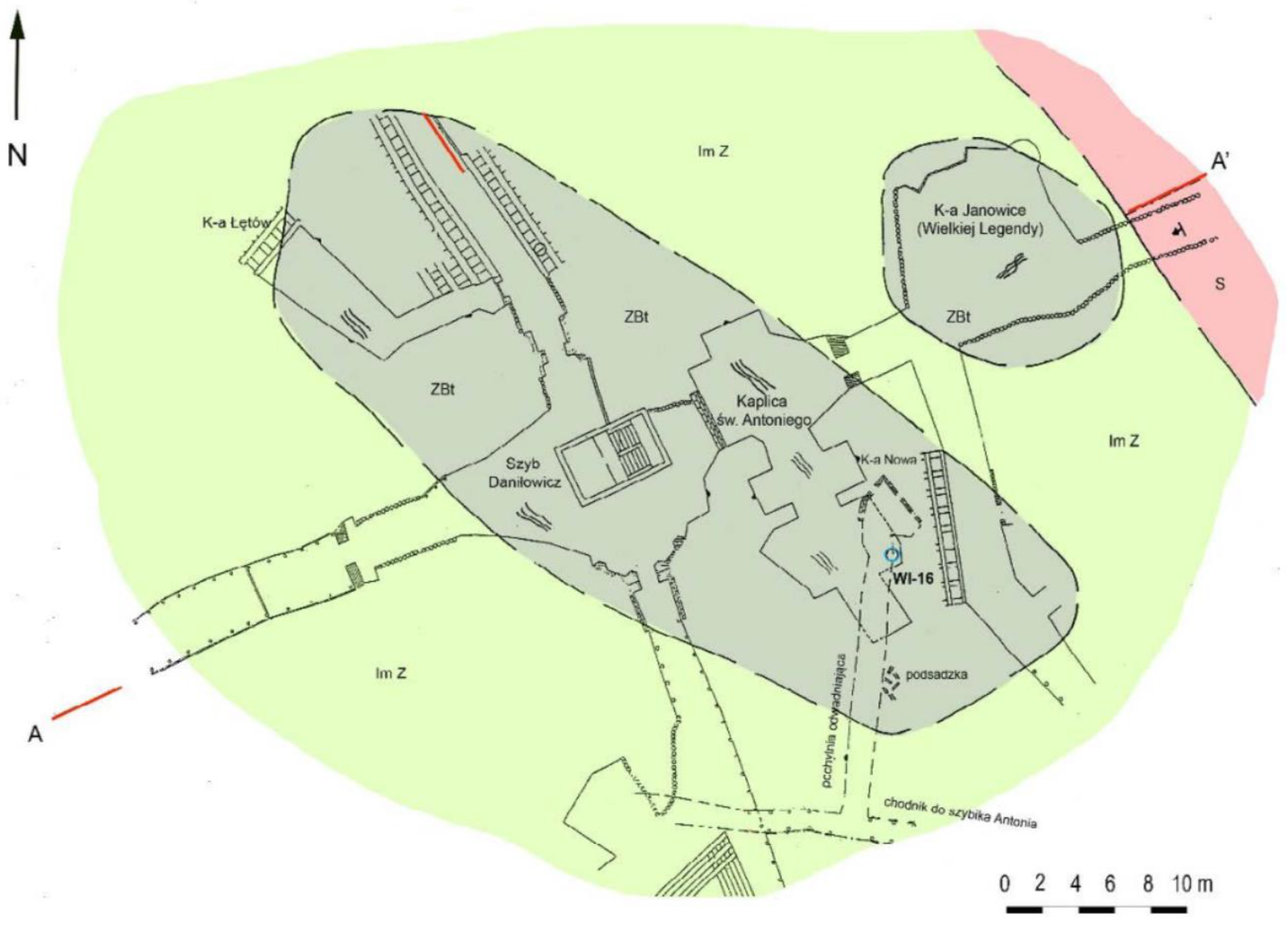
3.1. Study Sites
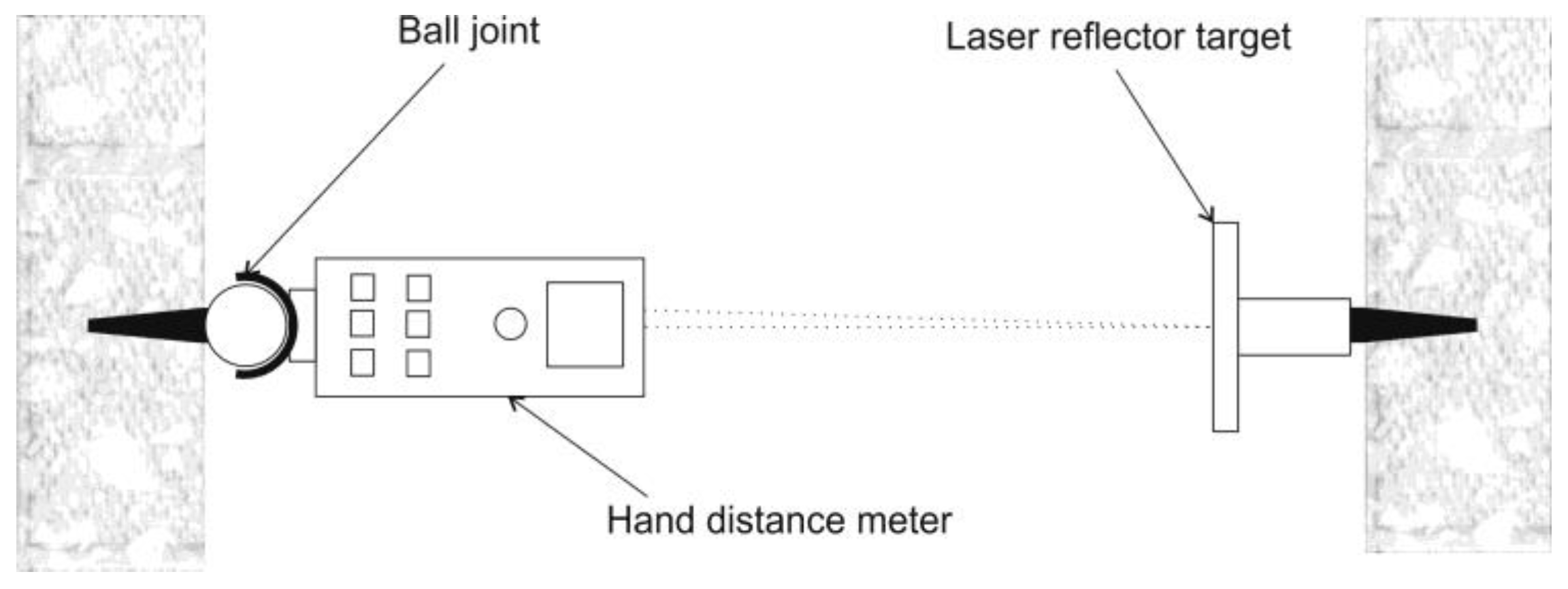
3.2. Convergence Measurement Methods of Mining Workings
3.3. Methods
4. Results
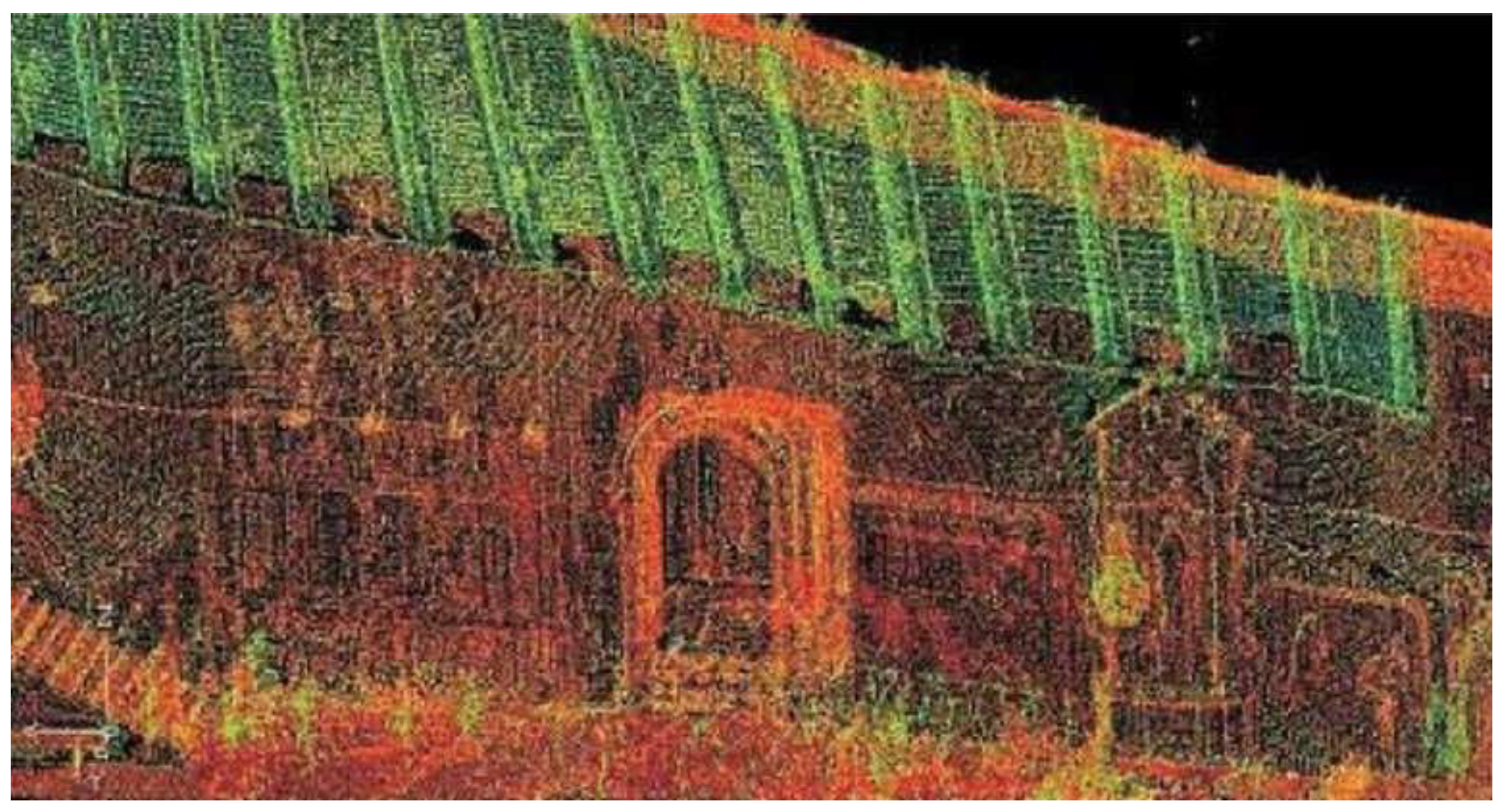
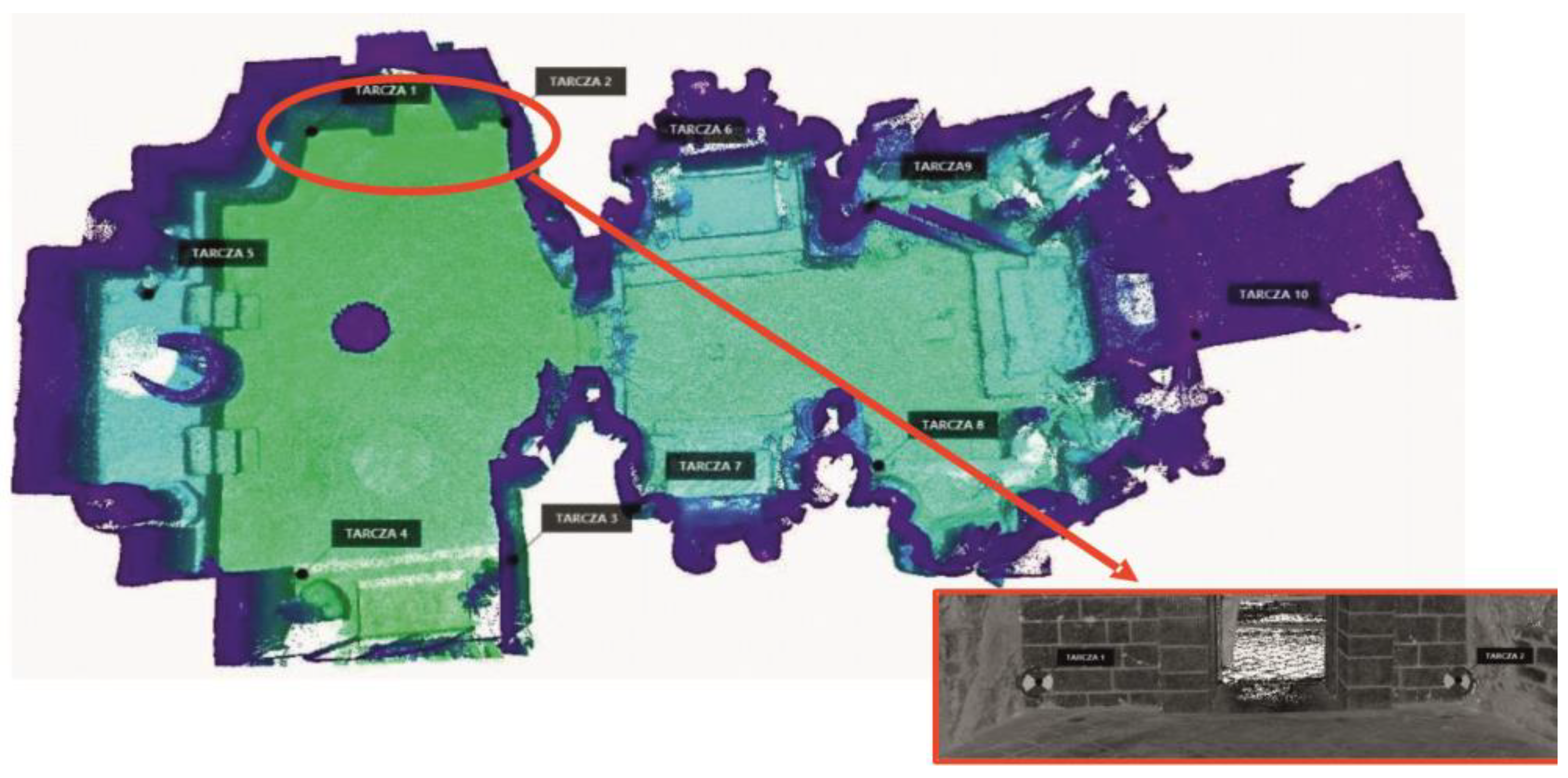
4.1. Quality of TLS Datasets and Direct Linear Station Measurement
4.2. Differential Models from Point Clouds With and Without Georeferencing
- Differential model 2012–2021, no georeferencing
- 2.
- Differential model 2012–2022. Cloud-to-cloud registration
- 3.
- Differential model 2012–2023. Cloud-to-cloud registration
- 4.
- Differential model 2012–2024. Cloud-to-cloud registration
- 5.
- Differential model 2022–2023, georeferenced
- 6.
- Differential model 2022–2024, georeferenced
5. Conclusions
- It is impossible to completely replace the traditional measurements with TLS if the same convergence monitoring method is used. The main reasons are the relatively poor repeatability and accuracy of indications from point clouds despite a high scanning resolution.
- The differential models demonstrated that registration based on an entity’s geometry yields less accurate values, even though it is a much faster method of adjusting point clouds to a common coordinate system.
- The differential models for the two registration methods can be used in mining engineering. The specific choice of method should hinge on the expected accuracy and degree of changes.
- The variant selected for the investigated excavation in the Wieliczka Salt Mine, where convergence is approximately one millimeter, was point cloud registration based on common georeferencing. The observed changes were minute, similar to the results of traditional observations, which confirms the process was completed correctly and the method selection was effective.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gawronek, P.; Kumosiński, W.; Kwinta, A.; Patykowski, G.; Zygmunt, M. Zastosowanie naziemnego skaningu laserowego w badaniu górniczych obiektów inżynierskich. Mies. Bezp. Pr. Ochr. Sr. Gór. 2016, 2, 14–22. (In Polish) [Google Scholar]
- Sălăgean, T.; Rusu, T.; Onose, D.; Farcaș, R.; Duda, B.; Sestraș, P. The use of laser scanning technology in land monitoring of mining areas. Carpathian J. Earth Environ. Sci. 2016, 11, 565–573. [Google Scholar]
- Kekeç, B.; Bilim, N.; Karakaya, E.; Ghiloufi, D. Applications of Terrestrial Laser Scanning (TLS) in Mining: A Review. Türk. Lidar Derg. 2021, 3, 31–38. [Google Scholar] [CrossRef]
- Salvini, R.; Francioni, M.; Riccucci, S.; Bonciani, F.; Callegari, I. Photogrammetry and laser scanning for analyzing slope stability and rock fall runout along the Domodossola?Iselle railway, the Italian Alps. Geomorphology 2013, 185, 110–122. [Google Scholar] [CrossRef]
- Zhang, J.-Y.; Li, H.-B.; Yang, X.-G.; Jiang, N.; Zhou, J.-W. Quantitative assessment of rockfall hazard in post-landslide high rock slope through terrestrial laser scanning. Bull. Eng. Geol. Environ. 2021, 80, 7315–7331. [Google Scholar] [CrossRef]
- Jones, E.; Beck, D. The use of three-dimensional laser scanning for deformation monitoring in underground mines. In Proceedings of the 13th AusIMM Underground Operators Conference: Paper No. 066, Gold Coast, Australia, 16–18 October 2017; pp. 267–270. [Google Scholar]
- Xu, J.; Wang, E.; Zhou, R. Real-time measuring and warning of surrounding rock dynamic deformation and failure in deep roadway based on machine vision method. Measurement 2020, 149, 107028. [Google Scholar] [CrossRef]
- Singh, S.K.; Banerjee, B.P.; Raval, S. Three-dimensional unique-identifier-based automated georeferencing and coregistration of point clouds in underground mines. Remote Sens. 2021, 13, 3145. [Google Scholar] [CrossRef]
- Wong, U.; Morris, A.; Lea, C.; Lee, J.; Whittaker, C.; Garney, B.; Whittaker, R. Comparative evaluation of range sensing technologies for underground void modeling. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 3816–3823. [Google Scholar]
- Mukupa, W.; Roberts, G.W.; Hancock, C.M.; Al-Manasir, K. A review of the use of terrestrial laser scanning application for change detection and deformation monitoring of structures. Surv. Rev. 2017, 49, 99–116. [Google Scholar] [CrossRef]
- Singh, S.K.; Banerjee, B.P.; Raval, S. A review of laser scanning for geological and geotechnical applications in underground mining. Int. J. Min. Sci. Technol. 2023, 33, 133–154. [Google Scholar] [CrossRef]
- Matwij, W.; Gruszczyński, W.; Puniach, E.; Ćwiąkała, P. Determination of underground mining-induced displacement field using multi-temporal TLS point cloud registration. Measurement 2021, 180, 109482. [Google Scholar] [CrossRef]
- Wang, L.; Li, J.; Jiang, C.; Huang, J. Automatic deformation extraction method of buildings in mining areas based on TLS point clouds. IEEE Access 2021, 10, 127817–127824. [Google Scholar] [CrossRef]
- Szwarkowski, D.; Moskal, M. Assessment of deformations in mining areas using the Riegl VZ-400 terrestrial laser scanner. In E3S Web of Conferences; EDP Sciences: Les Ulis, France, 2018; Volume 36, p. 02009. [Google Scholar]
- Li, J.; Wang, L. Mining subsidence monitoring model based on BPM-EKTF and TLS and its application in building mining damage assessment. Environ. Earth Sci. 2021, 80, 396. [Google Scholar] [CrossRef]
- Janus, J.; Ostrogórski, P. Underground mine tunnel modelling using laser scan data in relation to manual geometry measurements. Energies 2022, 15, 2537. [Google Scholar] [CrossRef]
- Archives of the Survey and Geology Department of Kopalnia Soli Wieliczka SA. (In Polish)
- Malinowska, A.; Hejmanowski, R.; Guzy, A.; Kwinta, A.; Ulmaniec, P. The Sinkhole Occurrence Risk Mitigation in Urban Areas for the Historic Salt Mine. Int. J. Environ. Sci. Sustain. Dev. 2019, 4, 85–94. [Google Scholar] [CrossRef]
- Hejmanowski, R.; Malinowska, A.; Kwinta, A.; Ulmaniec, P. Rock-mass stability in salt mines—Risk factors. In 12 Geokinematischer Tag; Freiberg, Germany, 2011; pp. 296–302. [Google Scholar]
- Karasev, M.A.; Protosenya, A.G.; Katerov, A.M.; Petrushin, V.V. Analysis of shaft lining stress state in anhydrite-rock salt transition zone. Rud.-Geol.-Naft. Zb. 2022, 37, 151–162. [Google Scholar] [CrossRef]
- Rzyczniak, M.; Solecki, M.; Zeljaś, D.; Dubiel, S. The effect of pressure depression on the water inflow volume to wells which cover carbonate rocks in the Carpathian Foredeep basement, SE Poland. Rud.-Geol.-Naft. Zb. 2021, 36, 33–42. [Google Scholar] [CrossRef]
- Teodorescu, P.P. Treatise on Classical Elasticity. Theory and Related Problems; Springer: Dordrecht, The Netherlands, 2013; p. 802. [Google Scholar]
- Sadd, M.H. Elasticity: Theory, Applications, and Numerics, Chantilly; Elsevier: Amsterdam, The Netherlands, 2009; p. 533. [Google Scholar]
- Bieniasz, J.; Wojnar, W. Zarys historii pomiarów i wybrane wyniki obserwacji zjawiska konwergencji wyrobisk w pokładowych złożach soli. Gospod. Surowcami Miner. 2007, 23, 133–142. (In Polish) [Google Scholar]
- Poborska-Młynarska, K. Water disasters in salt mining worldwide—Causes, counter, measures, consequences. Prz. Gór. 2018, 6, 33–40. (In Polish) [Google Scholar]
- Kortas, G.; Maj, A. Circumstances and consequences of catastrophic water inflow into the Wapno salt mine. Notes to the events of August 1977. Salt Rev. 2014, 34, 101–106. (In Polish) [Google Scholar]
- Bieniasz, J.; Pietras, J. Wykonanie pomiarów konwergencji wyrobisk górniczych w strefie ochrony konserwatorskiej w Kopalni Soli „Wieliczka”. In Ośrodek Badawczo-Rozwojowy Górnictwa Surowców Chemicznych „CHEMKOP” Sp. Z o.o. na Zlecenie Kopalni Soli „Wieliczka”; 2020. (In Polish) [Google Scholar]
- Gawronek, P.; Noszczyk, T. Does more mean better? Remote-sensing data for monitoring sustainable redevelopment of a historical granary in Mydlniki, Kraków. Herit. Sci. 2023, 11, 23. [Google Scholar] [CrossRef]






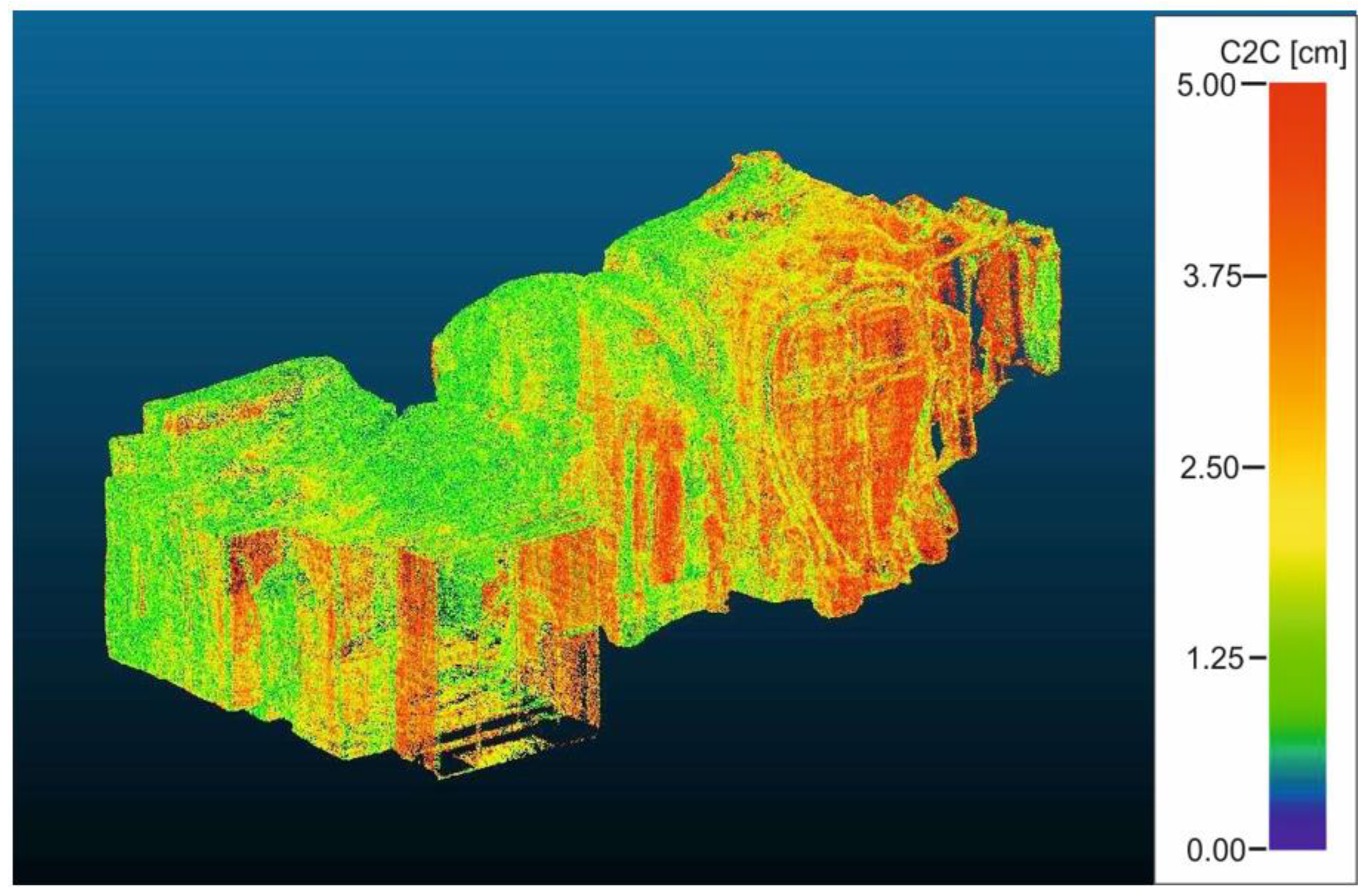



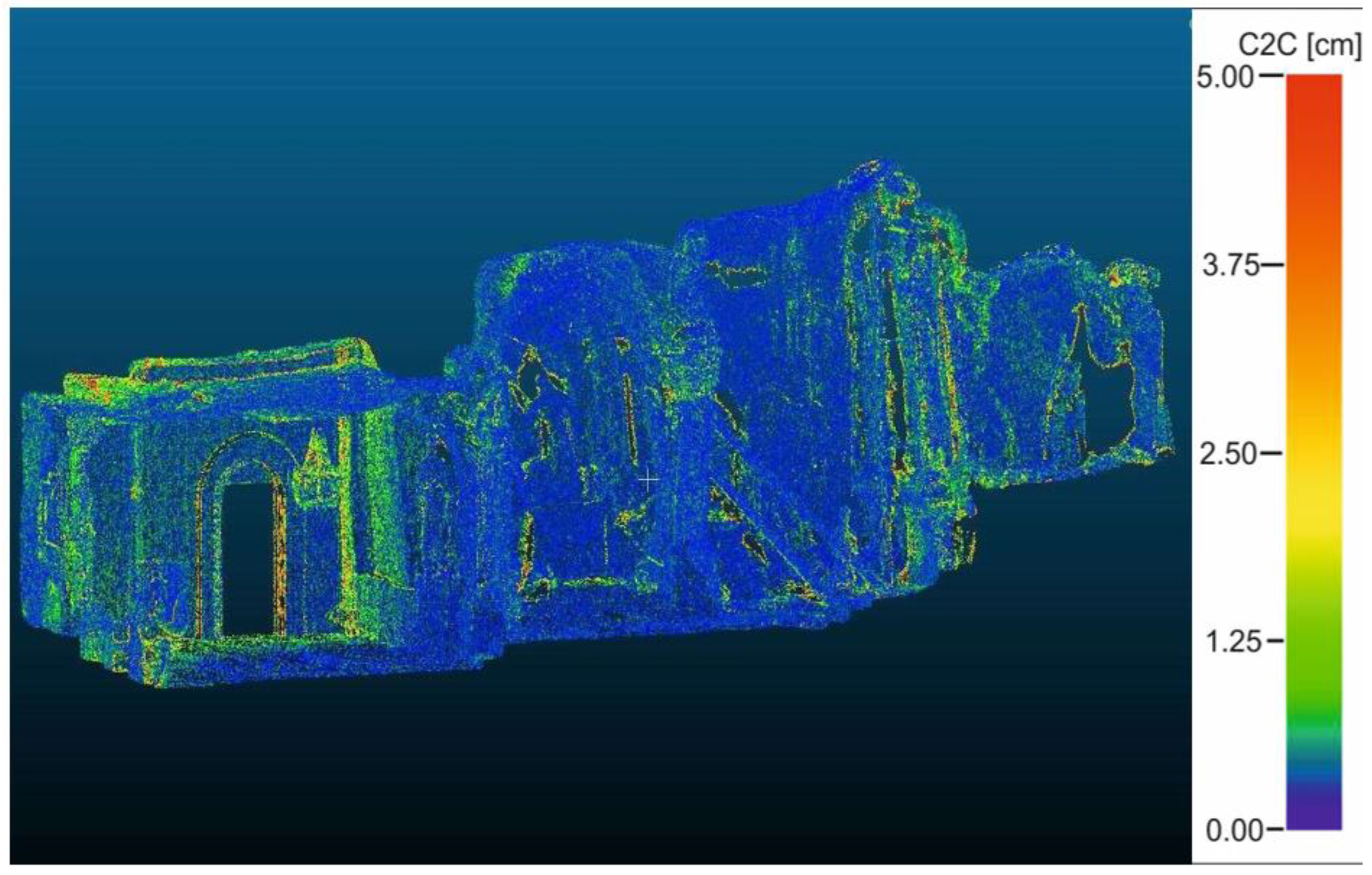

| Year | Base | Classical Measurement Length [m] | TLS Length [m] | Δd [mm] |
|---|---|---|---|---|
| 2012 | H1 | 7.444 | 7.439 | 5 |
| H2 | 15.491 | 15.495 | −4 | |
| V1 | 2.955 | 2.962 | −7 | |
| 2021 | H1 | 7.432 | 7.44 | −8 |
| H2 | 15.483 | 15.463 | 20 | |
| V1 | 2.938 | 2.926 | 12 | |
| 2022 | H1 | 7.436 | 7.438 | −2 |
| H2 | 15.484 | 15.485 | −1 | |
| V1 | 2.937 | 2.94 | −3 | |
| 2023 | H1 | 7.437 | 7.442 | −5 |
| H2 | 15.484 | 15.479 | 5 | |
| V1 | 2.934 | 2.94 | −6 | |
| 2024 | H1 | 7.436 | 7.439 | −3 |
| H2 | 15.482 | 15.486 | −4 | |
| V1 | 2.936 | 2.934 | 2 |
| Traditional Convergence Measurement | TLS Convergence Measurement | |
|---|---|---|
| measurement range | punctual | holistic |
| cost | low | high |
| time efficiency | measurement—long post-processing—fast | measurement—fast post-processing—long |
| required expertise | High | high |
| practical usability | Average | high, additionally, documentation of mining excavations |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gawronek, P.; Kwinta, A.; Sajdak, K.; Koczwara, P. TLS in Sustainable Mining Engineering: 3D Convergence and Surface Changes in Chamber Excavation in CH Salt Mine “Wieliczka”. Mining 2025, 5, 15. https://doi.org/10.3390/mining5010015
Gawronek P, Kwinta A, Sajdak K, Koczwara P. TLS in Sustainable Mining Engineering: 3D Convergence and Surface Changes in Chamber Excavation in CH Salt Mine “Wieliczka”. Mining. 2025; 5(1):15. https://doi.org/10.3390/mining5010015
Chicago/Turabian StyleGawronek, Pelagia, Andrzej Kwinta, Kamil Sajdak, and Piotr Koczwara. 2025. "TLS in Sustainable Mining Engineering: 3D Convergence and Surface Changes in Chamber Excavation in CH Salt Mine “Wieliczka”" Mining 5, no. 1: 15. https://doi.org/10.3390/mining5010015
APA StyleGawronek, P., Kwinta, A., Sajdak, K., & Koczwara, P. (2025). TLS in Sustainable Mining Engineering: 3D Convergence and Surface Changes in Chamber Excavation in CH Salt Mine “Wieliczka”. Mining, 5(1), 15. https://doi.org/10.3390/mining5010015








