Taxifolin Adsorption on Nitrogenated Graphenes: Theoretical Insights

Abstract

Solid-state drug delivery systems for the drug substances transport are of great importance nowadays. In the present work, the non-covalent interactions between taxifolin (Tax) and graphene as well as nitrogenated (N-doped) graphenes were systematically studied by using a wide set of theoretical techniques. Symmetry-adapted perturbation theory (SAPT0) calculations confirmed more favorable adsorption of Tax on N-doped graphenes compared to pristine graphene. It was established that dispersion interactions play the main role in the attractive interactions (>60%), whereas electrostatic and induction forces contribute only moderately to the attraction (~25% and 7–8%, respectively). Independent gradient model (IGM) analysis visually demonstrated the existence of dispersion interactions and hydrogen bonding in the studied Tax complexes. Ab initio molecular dynamics calculations indicated stability of these complexes at different temperatures. Our results show that N-doped graphenes with the enhanced interaction energy (E_int) toward Tax are promising candidates for the technical realization of the targeted drug delivery systems.

1. Introduction

In the last decade, scientific efforts have focused on the development of novel drug delivery systems (DDSs) for the transport of drug substances with marginal negative effects on the human organism. The need for highly efficient, flexible and controlled loading/release systems is driven by significant advances in patient compliance, clinical efficacy, and extended drug shelf life through controlled drug release. For these reasons, new DDSs have the potential to become one of the fastest growing segments of the pharmaceutical industry. It is believed that such systems can help one to overcome the limitation of bioavailability of different drugs and increase their efficiency for the introduction of novel therapies and theranostics. Current DDSs are based on nanostructural materials, and have been shown to offer substantial advantages, such as solubility, bioavailability, pharmacological activity, targeted delivery, and degradation [1,2,3].

Various available nanocarriers (e.g., carbon nanomaterials, metal and polymeric nanoparticles) have been widely used for drug delivery in cancer treatment [4,5,6]. Among them we may select graphene [7], graphene oxide [8], N-doped graphene [9], carbon nanotubes [10], and carbon nano-onions [11] as systems for drug delivery and release. Graphene-related materials have attracted much attention due to their biocompatibility [12] and valuable properties such as high specific surface area, ability for non-covalent π-π stacking, favorable interactions with various biomolecules, and high mechanical strength [8,13].

Taxifolin (Tax, dihydroquercetin) is a natural compound that belongs to the class of flavonoids. Much attention has been paid to Tax owing to its important pharmacological properties [14]. It is a powerful antioxidant with a pronounced effect in the prevention of several forms of cancer. Recently, it has shown promising suppressive activity against inflammation, malignancies, microbial infections, and cardiovascular and liver diseases. In present time, the protective role of Tax as a COVID-19 recovery is being evaluated (see, e.g., the recent review and the references therein [14]).

Different works reported a successful Tax release performance by zinc oxide nanoparticles [15], collagen-acrylic hydrogels [16], zein-caseinate nanoparticles [17], and cyclodextrine [18]. However, the papers dealing with interactions between Tax molecules and graphene derivatives are rather scarce. The bright examples are the work of Zhao et al. on quercetin, luteolin, and kaempferol adsorption on graphene oxide (GO) [19] and the paper of Tiwari et al. on quercetin adsorption on GO [20], and the report of Garcia et al. on a family of selected flavonoids and pristine graphene [21].

This work investigates adsorption properties of nanostructured platforms consisting of nitrogenated (N-doped) graphenes as nanocarriers loaded with the Tax molecule. N-doped carbon materials are among the most efficient metal-free catalysts [22]. It was found earlier that N-doping of graphene can slightly increase the activity of the oxygen reduction reaction, but N-doping at the graphene interface does not contribute significantly to the activity enhancement [23]. Also, N-doped graphenes have been studied for electrochemical sensing applications owing to their ability to enhance conductivity [24]. In addition to various catalytic applications, other applications can be found in medicine as N-doped graphene materials exhibit reduced cytotoxicity and antioxidant effects in a nitrogen content-dependent manner [25]. Moreover, N-doped graphene materials show less toxicity compared to GO [26].

More specifically, our aim is to perform a thorough comparative analysis of adsorption properties of graphene (G) and N-graphenes (pyrrolic (Npyrr-G), pyridinic (Npyrid-G) and quaternary graphene (2N-G)) toward Tax by using density functional theory (DFT), symmetry adapted perturbation theory (SAPT0) [27,28], the quantum theory of atoms-in-molecules (QTAIM) [29], and the independent gradient model (IGM) method [30,31]. Ab initio molecular dynamics (AIMD) simulations reveal the behavior of all complexes at room and liquid nitrogen temperatures. We suggest that the present theoretical study reveals the features of Tax/adsorbent interactions, indicating a promising future for nanoscale DDSs.

2. Computational Details

Geometries of the studied Tax complexes were optimized at the BLYP-D3/def2-SVP [32,33,34] level using the Orca 5.0.3 package [35]. Grimme’s dispersion correction (D3) was employed to properly treat van der Waals interactions [36]. The BLYP-D3 functional has been shown to provide reliable results on non-covalent complexes [37,38]. For each of these complexes, the total interaction energy (E_int) was calculated using the 0th-order symmetry-adapted perturbation theory (SAPT0) method [27] with the jun-cc-pVDZ basis set [39,40], which allows decomposing E_int to the exchange (E_ex), electrostatic (E_el), dispersion (E_disp), and induction (E_ind) components. It was established that such a combination of methods accurately predicts adsorption energies. SAPT0 calculations were carried out using the Psi4 code (v.1.4) [41]. It should be noticed that the more negative E_int value for a given complex denotes the stronger adsorption. The simplest SAPT0 method is defined in the following equation [28]:

$$E_{SAPT0}=E_{elst}^{\left(10\right)}+E_{exch}^{\left(10\right)}+E_{ind,resp }^{\left(20\right)}+E_{exch-ind,resp }^{\left(20\right)}+E_{disp}^{\left(20\right)}+E_{exch-disp }^{\left(20\right)}+{\delta }_{HF}^{\left(2\right)}$$

In this notation, $E^{\left(vw\right)}$ defines the order in V and in W_A + W_B in the Hamiltonian (H):

$$\mathrm{H}={\mathrm{F}}_{\mathrm{A}}+{\mathrm{W}}_{\mathrm{A}}+{ \mathrm{F}}_{\mathrm{B}}+{\mathrm{W}}_{\mathrm{B}}+\mathrm{V},$$

where the H is written as a sum of the usual monomer Fock operators (F), the fluctuation potential of each monomer (W), and the interaction potential (V); the subscript (resp) indicates that orbital relaxation effects are included.

The ${\delta }_{HF}^{\left(2\right)}$ term takes into account the higher-order induction effects, and it is included in the definition of SAPT terms.

Normally, the adsorption energy terms are calculated as following:

$$E_{int}=E_{el }+E_{ex }+E_{ind}+E_{disp },$$

where $E_{el }=E_{elst}^{\left(10\right)}$, $E_{ex }=E_{exch}^{\left(10\right)}$

$$\begin{gathered} E_{ind }=E_{ind,resp }^{\left(20\right)}+E_{exch-ind,resp }^{\left(20\right)}+{\delta }_{HF}^{\left(2\right)} \\ {E}_{disp }=E_{disp}^{\left(20\right)}+E_{exch-disp }^{\left(20\right)} \end{gathered}$$

We should briefly describe the components of the E_int energy term [42]. The electrostatic effect (E_el) describes the classical interactions between the static charge distributions of the interacting species. It may be either attractive (−) or repulsive (+). Induction effects (E_ind) arise from the distortion of a molecule in response to the electric field of all neighbor molecules, and they are always attractive (−). Dispersion interactions (E_disp) arise owing to instantaneous fluctuations of electron distributions of the molecules, and they are also attractive (−). The Pauli or exchange (E_ex) repulsion can be described from a classical point of view. The atomic approach results in a decrease in electron density in the internuclear region. As a result, the decreased screening of nuclear charges occurs, which leads to the increased nuclear-nuclear repulsion (+).

The studied model of graphene (G) consists of 48 carbon atoms. Three major cases of N-doped graphenes, namely pyrrolic (Npyrr-G), pyridinic (Npyrid-G) and quaternary graphene (2N-G) were also used as adsorbents. These models were chosen according to the experimental work on N-graphenes [43]. Their stability has been reported elsewhere [44]. The peripheral rims of all adsorbent models were saturated with hydrogen atoms to avoid dangling. The nanosheets of similar sizes have been recently employed as models for different adsorption studies [44,45].

The procedure for energy calculations was as follows. Firstly, to obtain the minimum energy structure, the Tax molecule was placed above the adsorbent sheet at a height corresponding the physisorbed state (~3.0 Å) and allowed to relax freely. The mutual initial configurations were randomized (see Figures S1–S4). The minimum energy configuration was used as the input configuration for SAPT0 calculations.

The initial structures for ab initio molecular dynamics (AIMD) simulations were also relaxed using the BLYP/def2-SVP method. All AIMD simulations used a time step of 1 fs, an NVT ensemble using a Nose–Hoover thermostat, and a velocity Verlet algorithm for integrating the equation of motion. The time period of 1000 fs has been used for the full AIMD computation cycle. These calculations were also done using the Orca 5.0.3 program suite.

The Multiwfn 3.8.0 program [46] has been used to obtain the independent gradient model (IGM) [30,31] isosurfaces and as well as obtaining the QTAIM parameters. VMD (v.1.9.3) [47] and Chemcraft [48] programs have been used for visualization aims. The detailed description of the IGM analysis has been given in the Supplementary Materials.

3. Results and Discussions

The models used for Tax, graphene and N-graphenes are demonstrated in Figure 1 and Figure 2.

Table 1. E_int and its constituents (kcal/mol) for interactions between Tax and the studied adsorbents. The values in parentheses denote the percentage contribution to attractive energy.

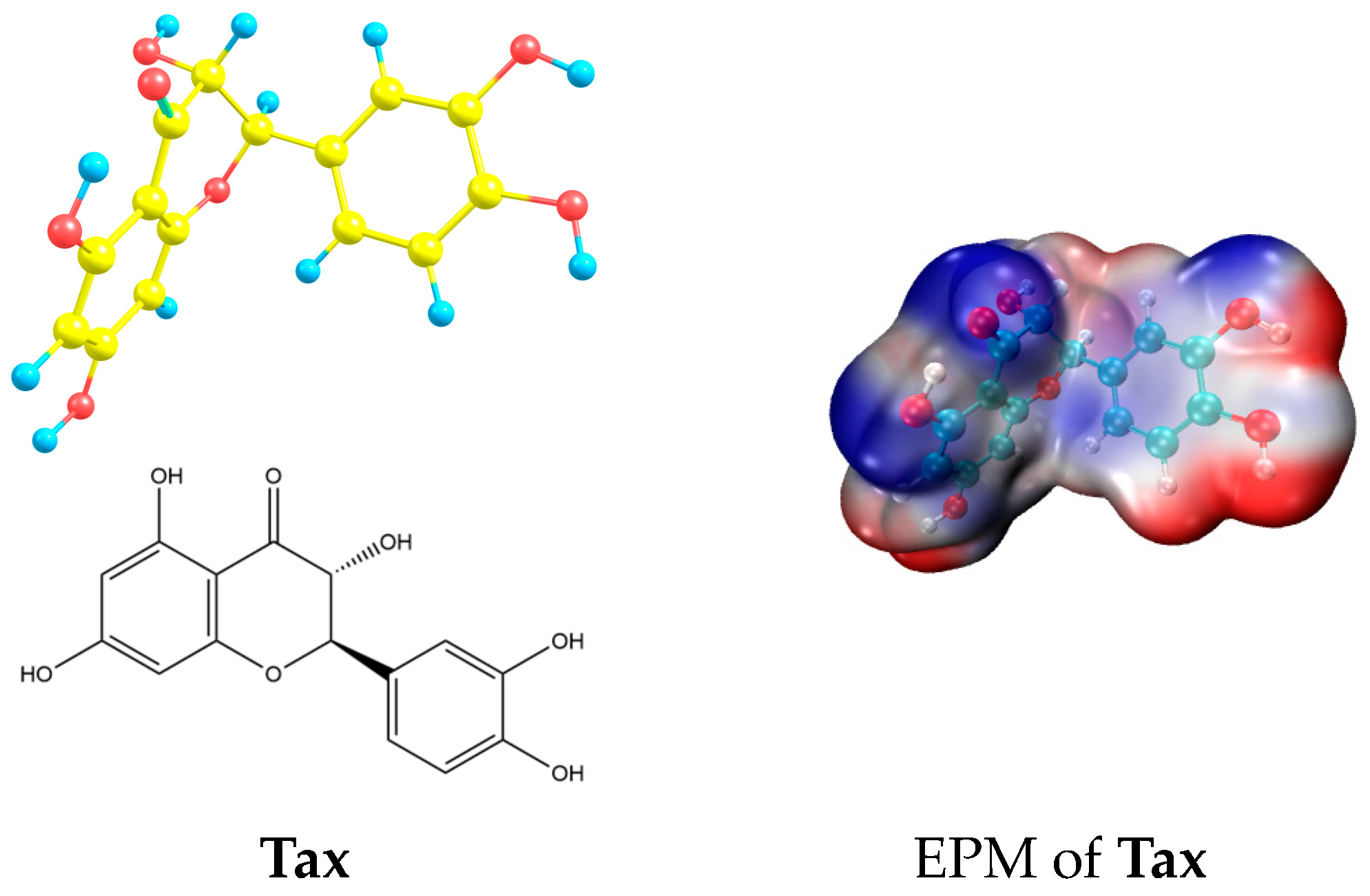
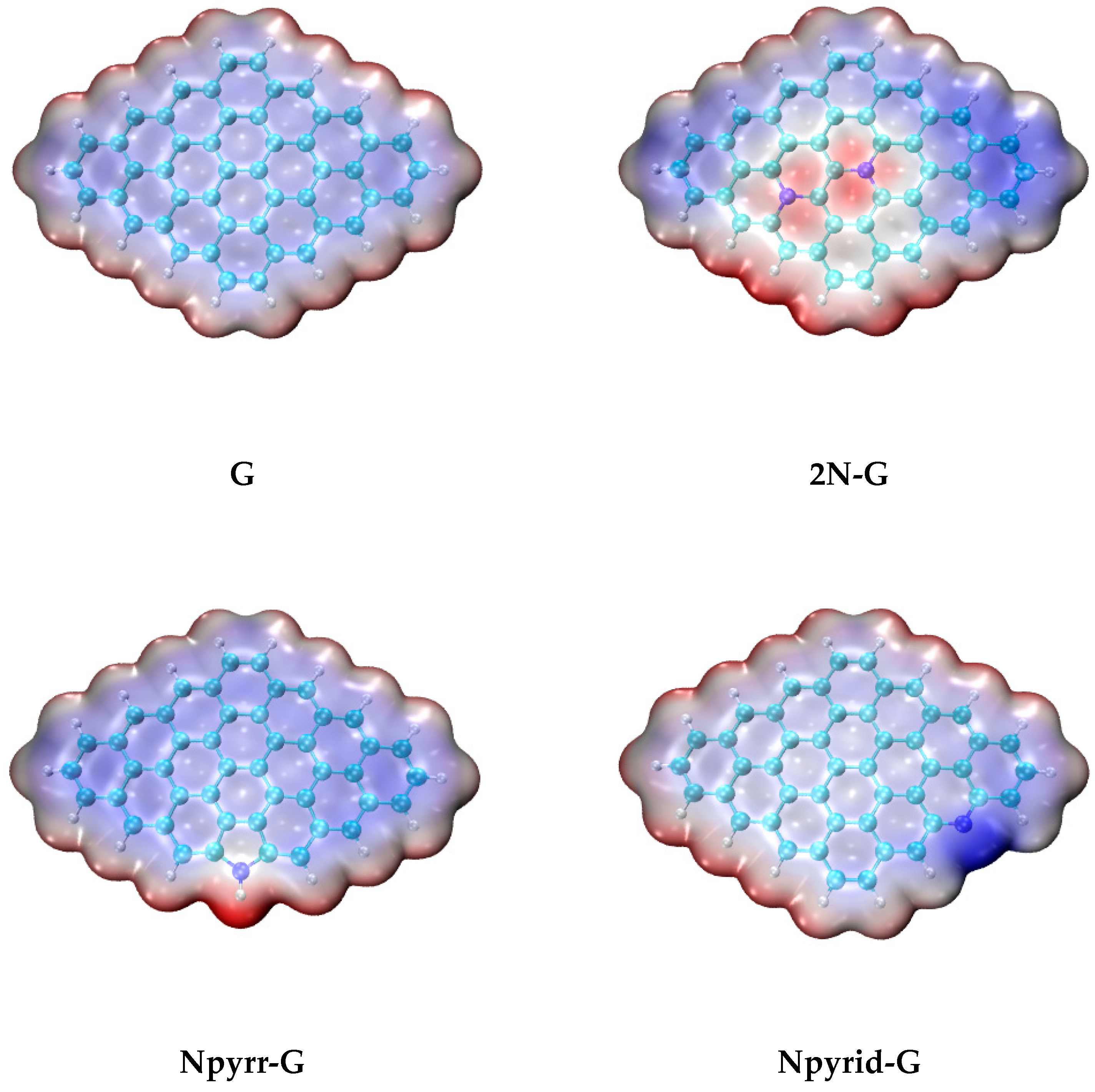
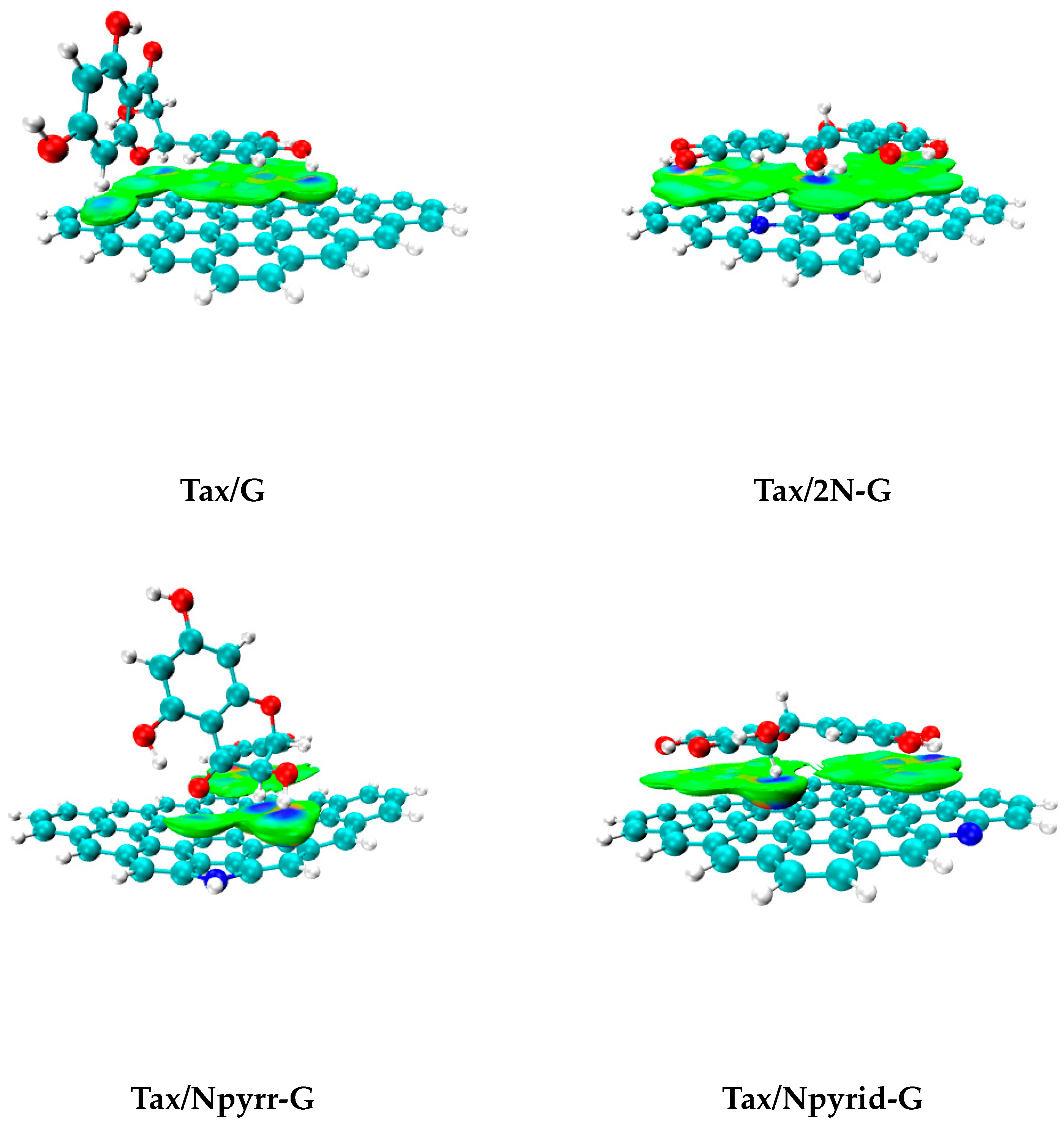
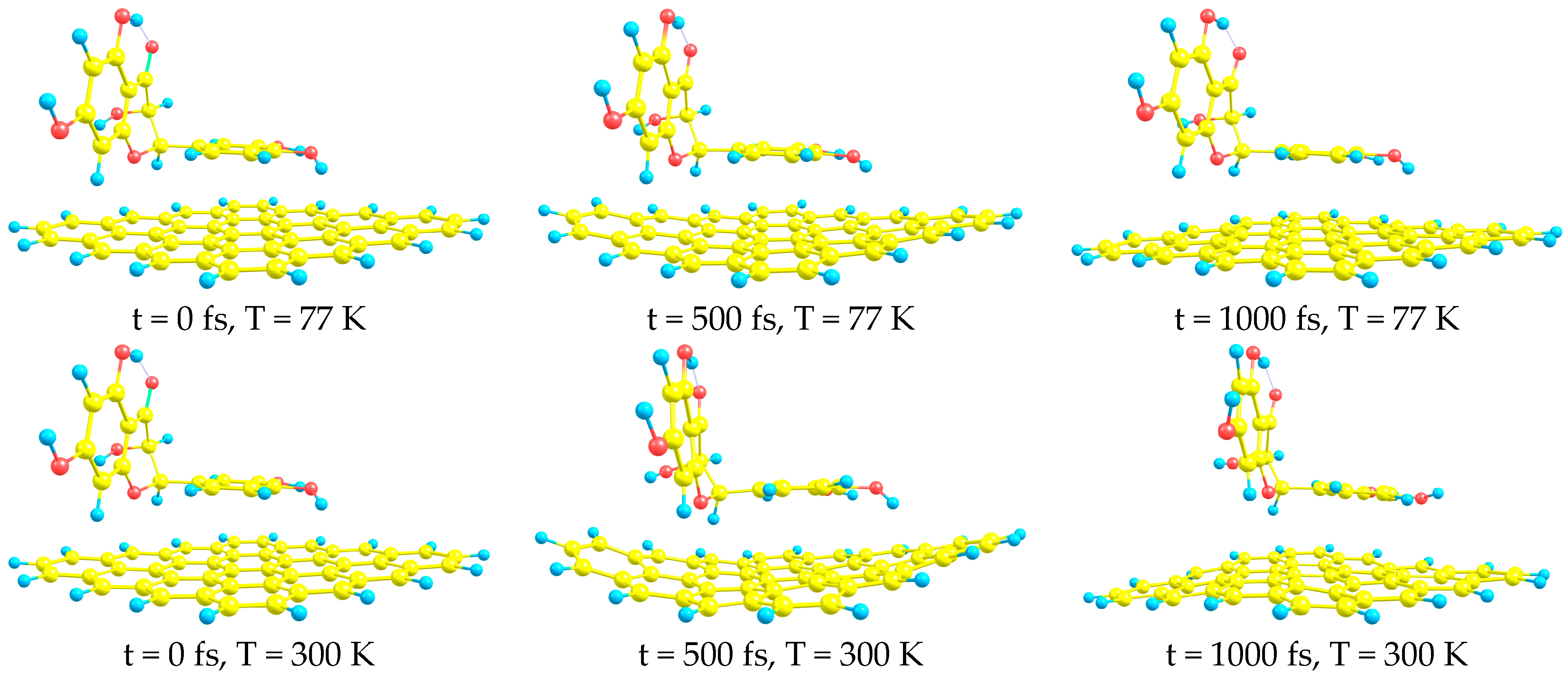
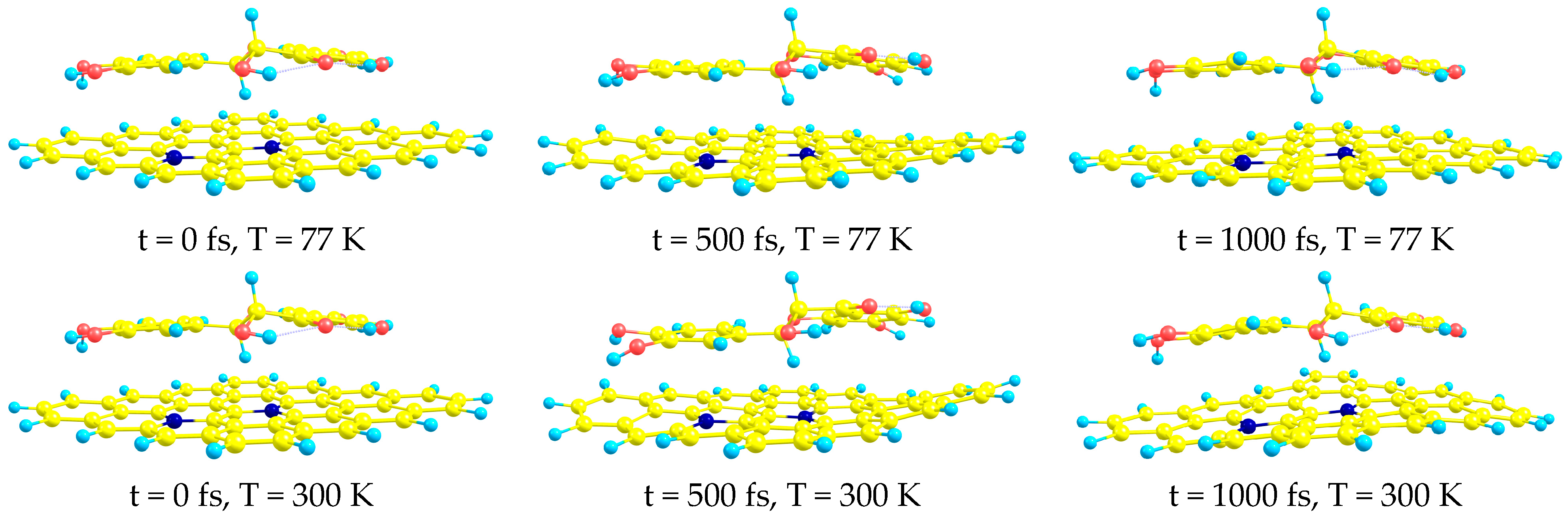
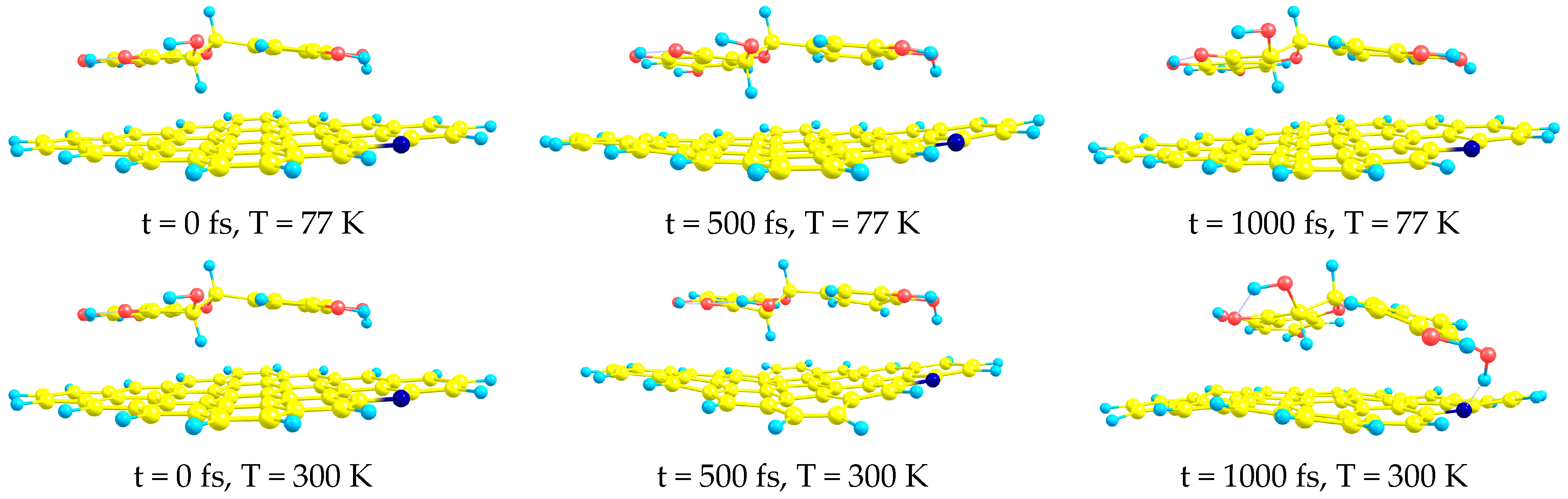
Adsorbent	Eint	Eel	Eex	Eind	Edisp
G	−30.04	−17.02 (25.0)	38.11	−4.80 (7.0)	−46.32 (68.0)
Npyrid-G	−37.16	−22.01 (23.8)	55.33	−7.46 (8.1)	−63.01 (68.1)
Npyrr-G	−32.63	−17.64 (23.3)	43.06	−6.21 (8.2)	−51.84 (68.5)
2N-G	−43.42	−28.34 (26.9)	62.12	−9.18 (8.7)	−68.02 (64.4)

shows the calculated interaction energy (E_int) and its constituents for Tax adsorption obtained at the SAPT0/jun-cc-pVDZ level of theory. To figure out the possible influence of the size of the adsorbent on the E_int values, we consider larger graphene sheets compared to the studied model. Generally, the widely used graphene model (circumcoronene) consists of 54 C atoms [49]. Also, we involve into consideration the graphene model consisting of 80 C atoms (Figure S5). The total E_int values are calculated to be −31.05 kcal/mol for the former and −33.72 kcal/mol for the latter. These values are in a good accordance with that for Tax adsorption on G presented herein (−30.04 kcal/mol). We, hence, proceed with the initial model.

First, we analyze the E_int energy term and its components for Tax adsorption. The magnitude of E_int for pristine graphene is the smallest one. At the same time, the gradual increase in E_int from Npyrr-G (−32.63 kcal/mol) to Npyrid-G (−37.16 kcal/mol) and further to 2N-G (−43.42 kcal/mol) is observed. It is of note, that the last case represents a much larger E_int value compared to E_int for graphene (~40%). To study these differences in detail, we now consider the electrostatic, inductive and dispersion contributions to the total attraction energy for all adsorbents. First, the marked increase in E_el can be observed for N-graphenes, except for the case of Npyrr-G (Table 1). The most significant E_el value of −28.34 kcal/mol is in the case of Tax/2N-G interactions. Besides this, only the 2N-G structure shows an increase in the relative contribution of E_el to E_int (26.9%).

We use electrostatic potential maps (EPMs) to further study electrostatic contributions in non-covalent interactions between the four adsorbents and Tax (Figure 1 and Figure 2). Blue areas characterize the abundance of electrons (negative charge), whereas red areas exhibit electron depletion (positive charge). For Tax, the negatively charged regions can be observed at O atoms, whereas positively charged regions are located at H atoms of OH groups (Figure 1). Figure 2 shows that, in contrast to the pristine G structure, all N-graphenes show non-uniform EPMs. 2N-G is characterized by the electron-depleted central area and electron-rich peripheral regions. At the same time, pyrrolic and pyridinic N atoms introduce marked changes at the edge of the Npyrr-G and Npyrid-G models, respectively. At a qualitative level, we may assume that the substituted benzene rings of Tax would interact with graphenes via π-π stacking. The OH-groups of Tax may preferably interact with the π-system of G and N-graphenes through H-bonding. As a whole, non-uniform EPMs of N-graphenes and especially of 2N-G will enhance intermolecular electrostatic interactions. These facts support our results obtained from SAPT0 calculations, which exhibit notable contributions of such interactions to the total attraction. The Mulliken charge transfer (CT) is calculated to be 0.031, 0.050, 0.064, and 0.025 e-towards G, 2N-G, Npyrid-G, and Npyrr-G, respectively. The larger CT values are attributed to the cases of larger interactions between Tax and N-graphenes (2N-G and Npyrid-G).

The independent gradient model (IGM) method allows the types of non-covalent interactions between interacting species to be obtained through a simple analysis of colored 3D isosurfaces. The isosurfaces obtained in the framework of IGM indicate the existence of two types of interactions between Tax and four adsorbents studied herein.

According to the IGM method, we can easily conclude that the stronger interactions (blue-colored areas of isosurfaces) are hydrogen bonding (H-bonding), and the weaker binding (green-colored areas of isosurfaces) is due to van der Waals interactions (Figure 3). The vast areas of green-colored isosurfaces are consistent with the results of SAPT0 calculations. This approves the importance of dispersion interactions for the favorable accommodation of Tax molecules on the surfaces of pristine graphene and N-graphenes. For the further examination of intermolecular interactions, we involve the Bader’s QTAIM analysis [29].

According to the Koch and Popelier’s QTAIM criteria for the existence of H-bonding, the following conditions should be fulfilled: first, the bond critical point (BCP) (3,−1) for the proton/acceptor contact exists; second, the electron density ρ(r) value for BCP (3,−1) should be in the range of 0.002 to 0.034 a.u.; and third, the corresponding Laplacian, ∇²ρ(r), should be in the range from 0.024 to 0.139 a.u. [50]. Additionally, there are factors indicating the existence of non-covalent interactions, and they are the following: (i) −G(r)/V(r) > 1 and (ii) the positive value of H(r). We analyzed the voids located in between the interacting Tax, graphene, and N-graphenes, and selected the corresponding BCPs (3,−1). The QTAIM data on BCPs for possible H-bonds between Tax and G are summarized in

Table 2. Topological parameters at the BCPs (3,−1) for the Tax/G complex.

No.	BCPs (3,−1)	ρ(r)	∇2ρ(r)	G(r)	V(r)	H(r)	−G(r)/V(r)
1	117	0.009	0.026	0.006	−0.005	0.0008	1.2
2	159	0.009	0.029	0.006	−0.005	0.0010	1.2
3	188	0.007	0.018	0.004	−0.003	0.0008	1.3
4	216	0.010	0.032	0.007	−0.006	0.0009	1.2

. The QTAIM parameters for Tax/2N-G, Tax/Npyrr-G, and Tax/Npyrid-G are given in

Table 3. Topological parameters at the BCPs (3,−1) for the Tax/2N-G complex.

Species	BCPs (3,−1)	ρ(r)	∇2ρ(r)	G(r)	V(r)	H(r)	−G(r)/V(r)
1	203	0.017	0.050	0.012	−0.011	0.0008	1.09
2	246	0.006	0.017	0.004	−0.003	0.0004	1.33
3	277	0.008	0.022	0.005	−0.004	0.0007	1.25
4	287	0.015	0.036	0.008	−0.008	0.0006	1.00

,

Table 4. Topological parameters at the BCPs (3,−1) for the Tax/Npyrr-G complex.

Species	BCPs (3,−1)	ρ(r)	∇2ρ(r)	G(r)	V(r)	H(r)	−G(r)/V(r)
1	153	0.013	0.041	0.009	−0.008	0.0009	1.13
2	161	0.008	0.024	0.005	−0.004	0.0009	1.25
3	199	0.015	0.039	0.009	−0.009	0.0005	1.00
4	226	0.011	0.033	0.007	−0.006	0.0009	1.17

and

Table 5. Topological parameters at the BCPs (3,−1) for the Tax/Npyrid-G complex.

Species	BCPs (3,−1)	ρ(r)	∇2ρ(r)	G(r)	V(r)	H(r)	−G(r)/V(r)
1	138	0.007	0.018	0.004	−0.003	0.0008	1.33
2	168	0.016	0.050	0.011	−0.009	0.0015	1.22
3	236	0.005	0.013	0.003	−0.002	0.0006	1.50

, respectively. We verify three, two, four and one intermolecular H-bonds in the Tax/G, Tax/2N-G, Tax/Npyrr-G, and Tax/Npyrid-G complexes, respectively. Additionally, the existence of non-covalent bonding has been proved. To sum up, according to the QTAIM analysis, all the complexes exhibit both non-covalent interactions between species and H-bonding. No indicators of covalent bonding have been found.

The next component of interest is the induction interactions. The E_ind term contributes only marginally to the total attraction (~7–8%). Although absolute values of E_ind increase from G to N-graphenes (−4.80 (G), −7.46 (Npyrid-G), −6.21 (Npyrr-G), and −9.18 (2N-G) kcal/mol), its relative contribution remains nearly the same (we can see only small increase of 1–2%) (Table 1). It witnesses that permanent dipole moments of N-graphenes (3.18, 1.95, and 3.28 D for 2N-G, Npyrr-G, and Npyrid-G, respectively) affect the strength of intermolecular interactions, and it leads to more favorable Tax adsorption. These effects, however, are rather small, and the E_ind term contributions are smaller than those of E_el.

We now turn to the discussions on London dispersion interactions, which contribute significantly to attraction in all cases (see Table 1 and Figure 3). For G and N-graphenes, the E_disp relative contributions are of roughly the same magnitude, but there is a striking difference in their absolute values. Indeed, E_disp increases by absolute value from −46.32 (G) to −68.02 (2N-G) kcal/mol. Moreover, its relative contribution to the attractive interactions is very large (>60%), and the order of the energy constituents is as follows: E_disp > E_el > E_ind. From the analysis of the relative inputs of energy terms to attraction, it becomes clear that the dispersion term is roughly several per cent smaller in the 2N-G case and that this is compensated for by a simultaneous increase in the induction and electrostatic contributions.

Our previous work studied Tax interactions with a fragment of the arabinogalactan molecule [51]. In contrast to the present report, the E_el and E_disp terms were of almost equal importance for the stabilization. In addition, we detect numerous H-bonds between two interacting species. Another theoretical work studied adsorption of different flavonoids (quercetin, luteolin, and kaempferol) on graphene oxide [19]. It was established that the main driving force for favorable adsorption are π-π interactions and H-bonding. As a whole, our conclusions are similar to those obtained previously [19], but the SAPT0 method is not able to separate H-bonding from E_int. Instead of that, the substantial portion of H-bonding is included in the E_ind term. However, in our case, the E_ind terms are rather small, and, supposedly, the E_disp dominates.

We further compare behavior of all studied complexes at different temperatures (T = 77 K (liquid nitrogen temperature) and T = 300 K (room temperature)) by using results of ab initio molecular dynamics (AIMD) simulations. Although both classical MD [52] with empirically derived forces and AIMD with forces derived from DFT calculations can be suitable for this purpose, we select the AIMD method. It becomes popular owing to its advantages, e.g., transferability between systems and ability to accurately describe polarization and charge transfer [53]. For the Tax/G complex and T = 77 K, we observe only minor changes in the mutual configuration of the complex (Figure 4). The arrangement of Tax and G species is preserved during the whole period of simulation. Only small changes in the framework of G can be observed. For T = 300 K, the larger changes of the framework of G can be noticed, and the sheet of G acquires the corrugated shape. At the same time, the distances between Tax and G are nearly equal during the simulation time.

A similar situation exists for the Tax/2N-G complex and T = 77 K (Figure 5). We may observe only marginal changes in both the molecular geometry and the distances between Tax and 2N-G. For T = 300 K, the 2N-G sheet acquires a slightly curved shape, but generally smaller changes compared to the previous case can be noticed. In all considered cases, the Tax molecule is in the physisorbed state throughout the simulation.

For the Tax/Npyrr-G complex and T = 77 K, we detect very small mutual reorientations of Tax and Npyrr-G species (Figure 6). For the higher T = 300 K, the displacement of Tax is slightly larger, but it generally retains its initial location. The framework of Npyrr-G is almost intact in these two cases. For the Tax/Npyrid-G complex (Figure 7), we can detect very small displacements for the lower T = 77 K, and slightly larger displacements/distortions for the case of T = 300 K. No sufficient shifts of Tax from the initial positions can be found for Tax/Npyrid-G simulations. The distances between the center-of-mass (COM) of Tax and studied N-graphenes are summarized in Table S1. They are determined as the perpendicular line dropped from the COM to the underlying surface. While the simulation is proceeding, changes of the distances are taking place in studied systems. The comparison of the distances shows that the travelling of Tax is much smaller in the case of T = 77 K, and the larger distance can be observed in the case of Npyrr-G (>4 Å). As a whole, the AIMD analysis confirms the stable behavior of Tax adsorbed on both pristine graphene and N-doped graphenes.

In addition to this, it is worth considering the solvent effects on the studied complexes as solvent environments in DDSs are important for their accurate description [54]. The first solvent used is water. We should keep in mind that Tax has a poor solubility in pure water, and the large graphene clusters are hydrophobic. It must also be kept in mind that the Tax molecules change its solubility markedly with change of temperature, and the small graphene clusters (like those involved in the present work) are water-soluble [55]. We, therefore, use water as a reference by adding explicitly six water molecules in the void between Tax and N-graphenes (Figure S6). A 50% ethanol–water mixture was also employed in this work as the second solvent as this mixture allows Tax to be dissolved. To mimic this solvent, we add the 3:3 ratio of water and ethanol molecules. For the aim of comparison, gas phase calculations were also made.

Now we calculate the E_int,s values based on the supermolecular approach (

Table 6. E_int,s (kcal/mol) for interactions between Tax and the studied adsorbents obtained via the supramolecular approach.

Adsorbent	Eint,s No Solvent	Eint,s 3:3 w:e	Eint,s 6 w
G	−33.02	−130.00	−141.58
Npyrid-G	−44.30	−146.90	−144.52
Npyrr-G	−32.63	−143.68	−139.42
2N-G	−50.65	−142.12	−145.85

).

$${\mathrm{E}}_{\mathrm{int},\mathrm{s}}={\mathrm{E}}_{\mathrm{comp} }-{\mathrm{E}}_{\mathrm{Tax} }-{ \mathrm{E}}_{\mathrm{N}-\mathrm{graphene}}-{\mathrm{E}}_{\mathrm{solv} }$$

where E_comp is the energy of the studied complex, E_Tax is the energy of Tax, E_N-graphene is the energy of corresponding N-graphene, and E_solv is the energy of solvent molecules used.

When being involved, the solvents lead to a substantial stabilization of all complexes (Table 6). The E_int,s change varies from a three (2N-G) to an almost five times (Npyrr-G) increase. We link this behavior with the formation of numerous H-bonds between the studied species and solvent molecules. This indicates the applicability of studied adsorbents as Tax DDSs. It should be mentioned, though, that the large magnitudes of interaction energies may complicate the drug release. To avoid this possible problem, one should modify the graphene surface or select the solvent with care. Recent papers describe the endogenous and exogenous stimuli-responsive drug delivery [56,57]. The former includes pH-sensitive, redox-responsive, and ROS-responsive (reactive oxygen species) drug delivery and release. The latter deals with NIR-responsive, thermo-responsive, and electro-responsive drug delivery. Yang et al. report the strong pH dependence of loading and release of doxorubicin hydrochloride on the graphene oxide surface. They claimed that such a dependence may be caused by the stronger H-bonding interactions under basic conditions than those under acid conditions [58]. We assume that the similar technique can be suitable for Tax.

To summarize, based on the present results and those obtained elsewhere, we highlight the possible ways of use for N-doped graphene. Theoretical investigations of the non-covalent interactions between the surface of graphene and related materials from the one side and different molecules from the other side can solve the problems in applying graphene materials. The main areas of interest are biological, environmental, and material science prospective applications [59]. Based on the non-covalent interactions between graphene and various molecules, we can expect the excellent nanotechnology applications in the fields of DDSs (the results of the present work), cancer treatment, energy storage, and bioimaging. Molecular adsorption can be fine-tuned by the doping with N atoms. Such a method allows obtaining enhanced E_int magnitudes for adsorbate molecules. Indeed, Table 1 shows enhanced E_int values for Tax adsorption on N-graphenes compared to pristine graphene. Such graphenes can act as a substitute for Li, Na, K-decorated graphenes, providing increased E_int values for adsorption of small molecules. At the same time, N-graphenes are easier to handle, because there is no need to manipulate with single atoms when they are involved as an adsorbent. Another important aspect is the stability and high Young’s modulus of such structures [60]. This allows N-graphenes to be used in complex adsorbent systems, where high durability is required.

4. Conclusions

To conclude, in this report, we study non-covalent interactions between the Tax molecule, G, and three N-graphenes. We obtained E_int values and conducted SAPT0 energy decomposition analyses of four complexes. We found a more favorable binding of Tax on N-graphenes compared with their pristine counterpart. The detailed outcomes are as follows:

(1)

N-doping of G leads to the substantial increase in E_int for Tax adsorption. The highest E_int value is in the case of 2N-G (−43.42 kcal/mol), and it is much larger than that for G (−30.04 kcal/mol).

(2)

SAPT0 calculations revealed that dispersion interactions play the main role in the stabilization of Tax (64–68%). Induction interactions contribute little to total attractions (7–8%), and the effects of electrostatic interactions fall between them (23–26%).

(3)

IGM graphs visually represent the dominant character of dispersion interactions. Besides this, the existence of strong interactions (H-bonding) was revealed. The QTAIM method approves the existence of H-bonding in all the studied complexes.

(4)

AIMD simulations confirm the stability of all complexes at both studied temperatures (T = 77 and T = 300 K).

The obtained results are of special importance for further experimental and theoretical research of N-doped graphenes as systems for DDSs, in particular in the field of study of natural compounds with excellent pharmacological properties.