A Simplified Way to Evaluate the Effect of Temperature on a Circular Tunnel
Abstract
:1. Introduction
- (1)
- Seasonal changes in ambient temperature: Luo et al. [1] have shown that the temperature of lining varies with the seasonal changes. For instance in their study, the temperature variation was between −1.8 °C in winter and 13.2 °C in summer.
- (2)
- Heating from the trucks, trains or passage of cars. Nicholson et al. [2] carried out an assessment of the available heat energy inside tunnels. They found that train heat emitted from the brakes, motors and air conditioning systems, could be able to warm the surrounding ground and the air.
- (3)
- Geothermal issues: Shallow geothermal energy is available all over the world (below 10 m to 400 m under the ground) [2]. The underground geotechnical structures, such as tunnel linings, have large structure-ground interfaces and can easily be converted as heat-exchangers [3,4,5,6]. Therefore, the temperature of lining may also change because of geothermal energy.
- (4)
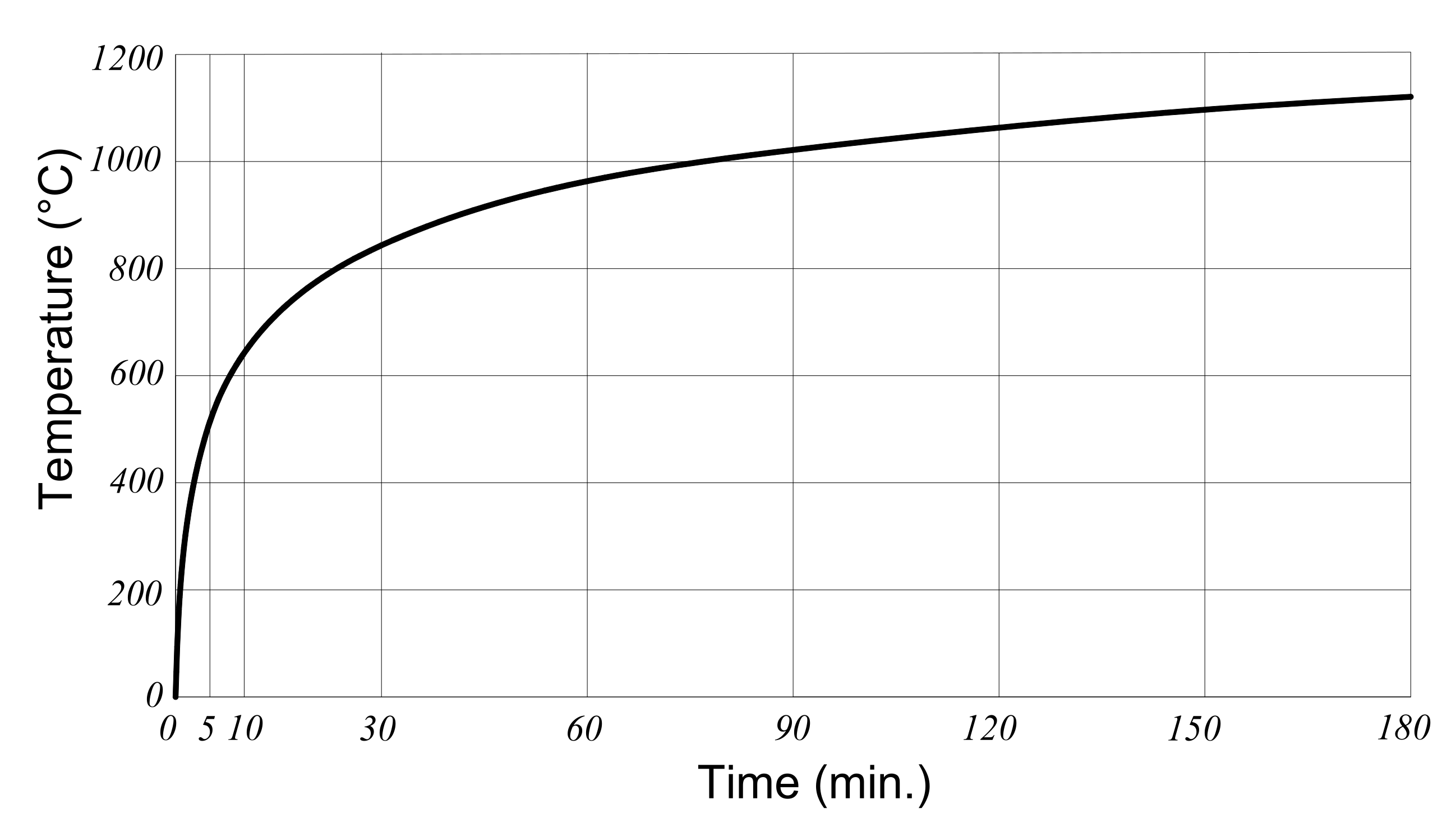
- Fires: Emergency situations such as fires could be able to cause the temperature change in tunnels [7]. It was investigated by Maraveas and Vrakas [8] that a fire occurring in tunnel induces a rapid rise of the air temperature, to more than 1000 °C, within a few minutes. This rapid change of temperature results in an explosive concrete spalling of the tunnel lining [9], which not only brings about casualties and property loss, but also causes a prolonged disruption of operations.
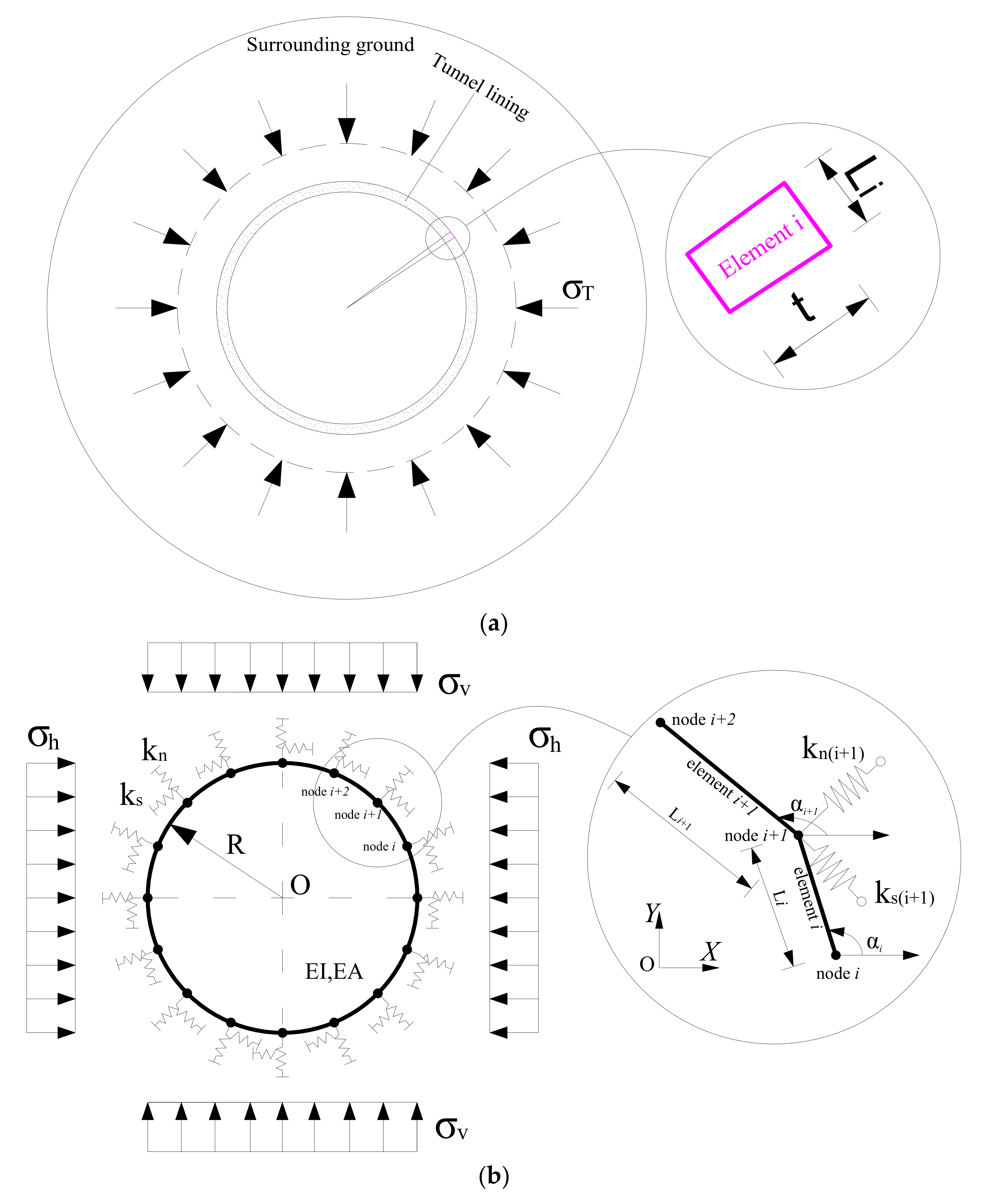
2. HRM Method
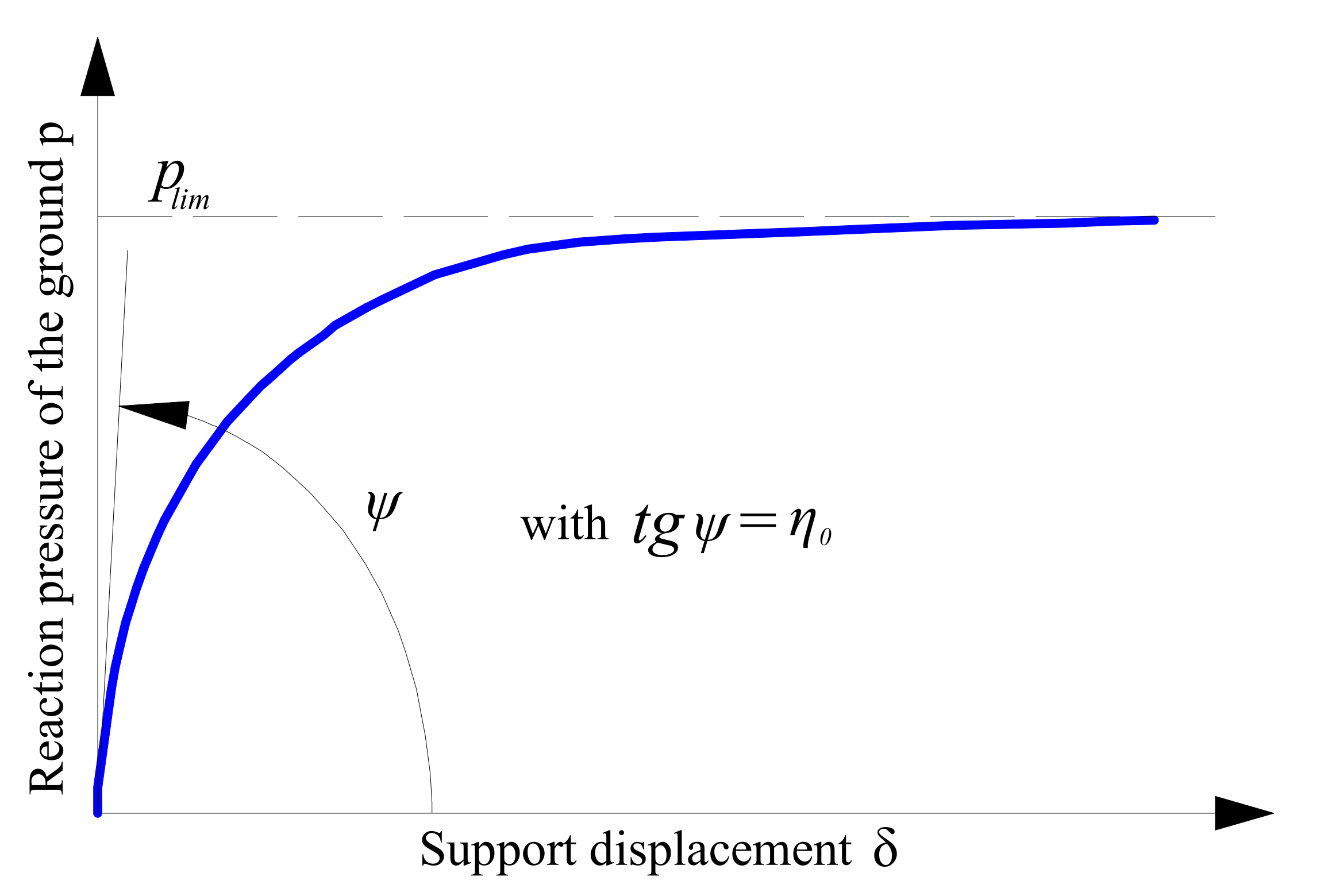
2.1. Interaction of the Ground and Structure
2.2. Loads Applied to the Lining
2.2.1. Active Loads
2.2.2. Additional Thermal Loads
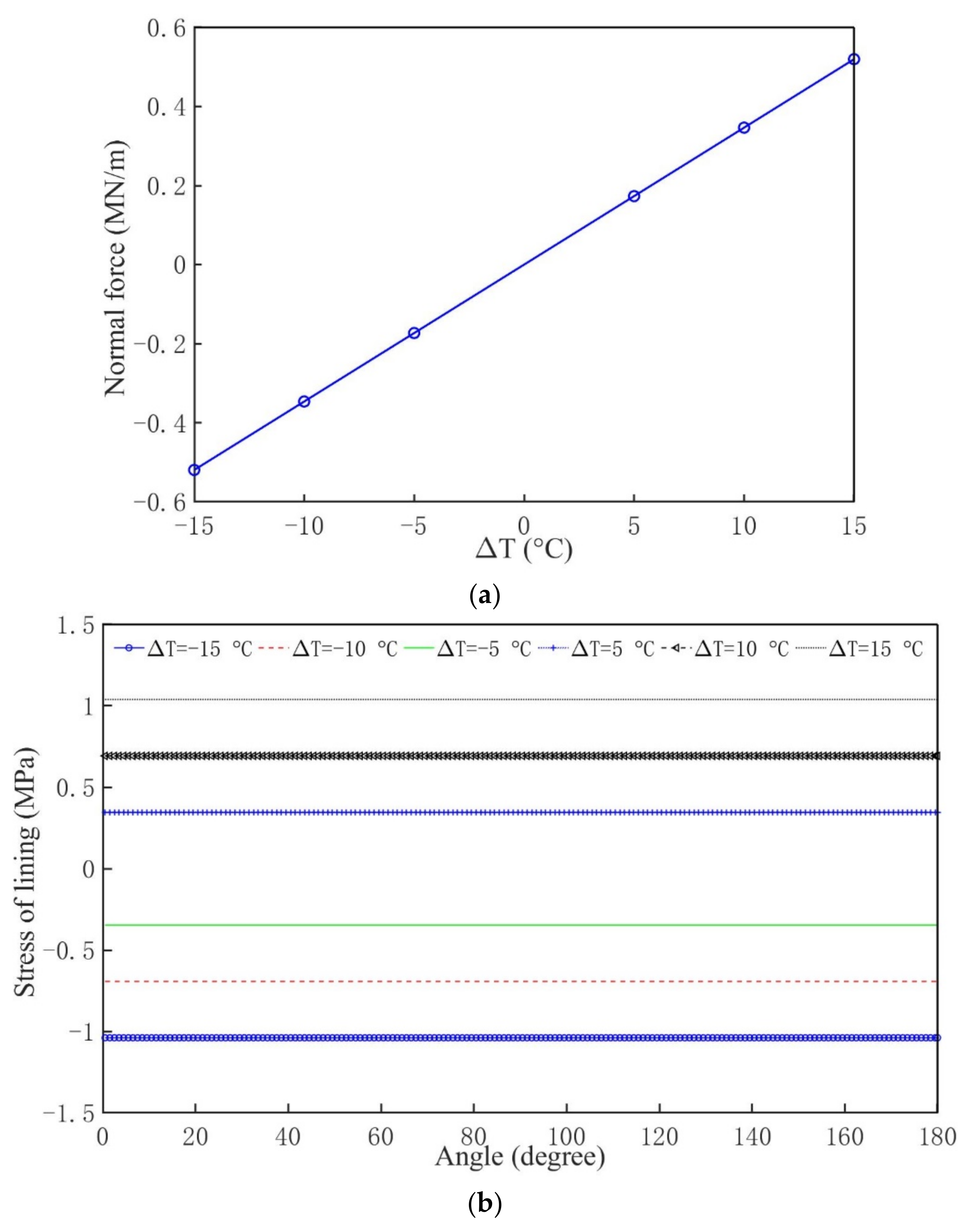
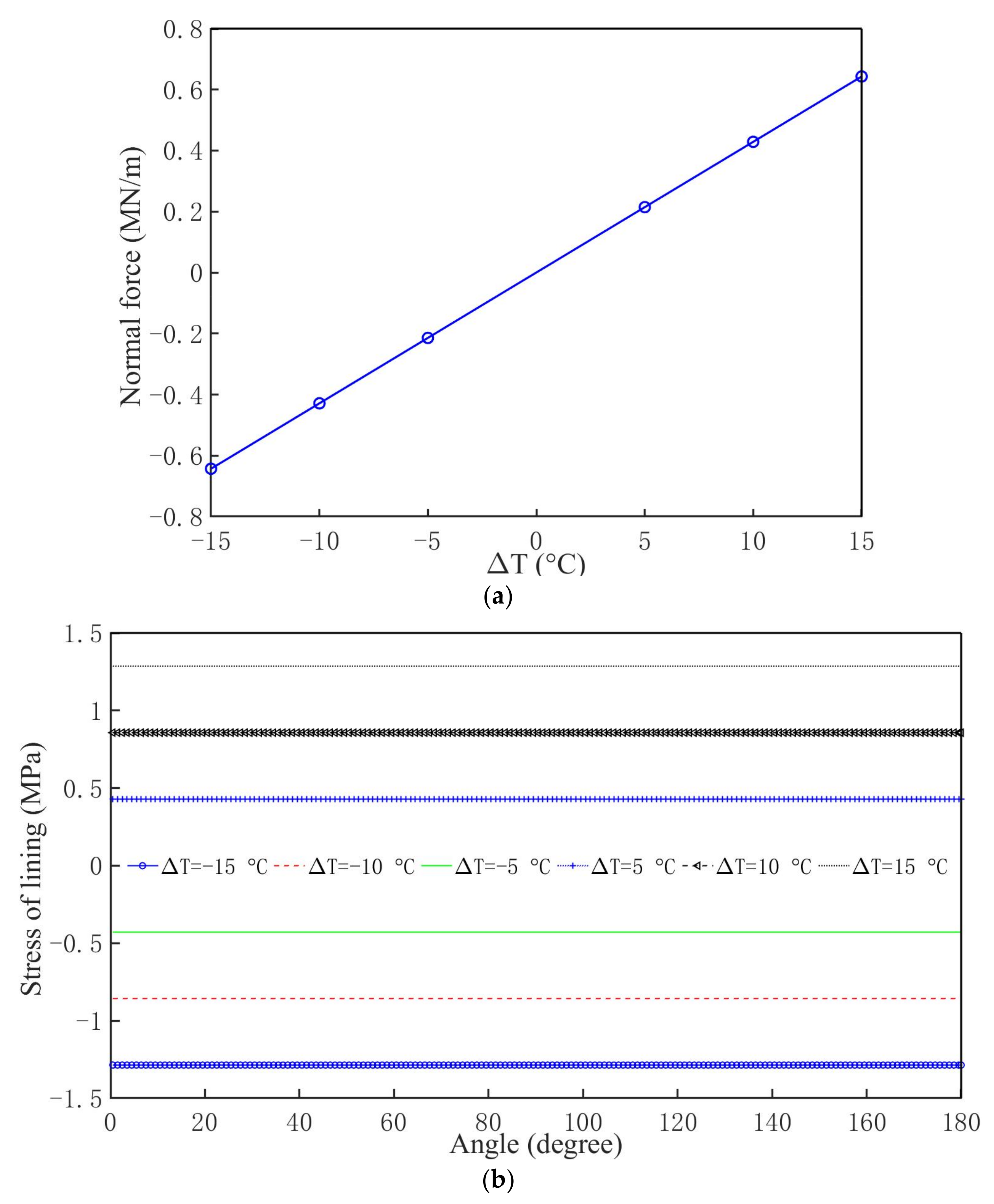
3. Impact of ∆T on the Internal Forces of Tunnel Lining
3.1. Only Considering
3.2. Considering and
3.3. Impact of Other Factors on the Internal Forces of Tunnel Lining
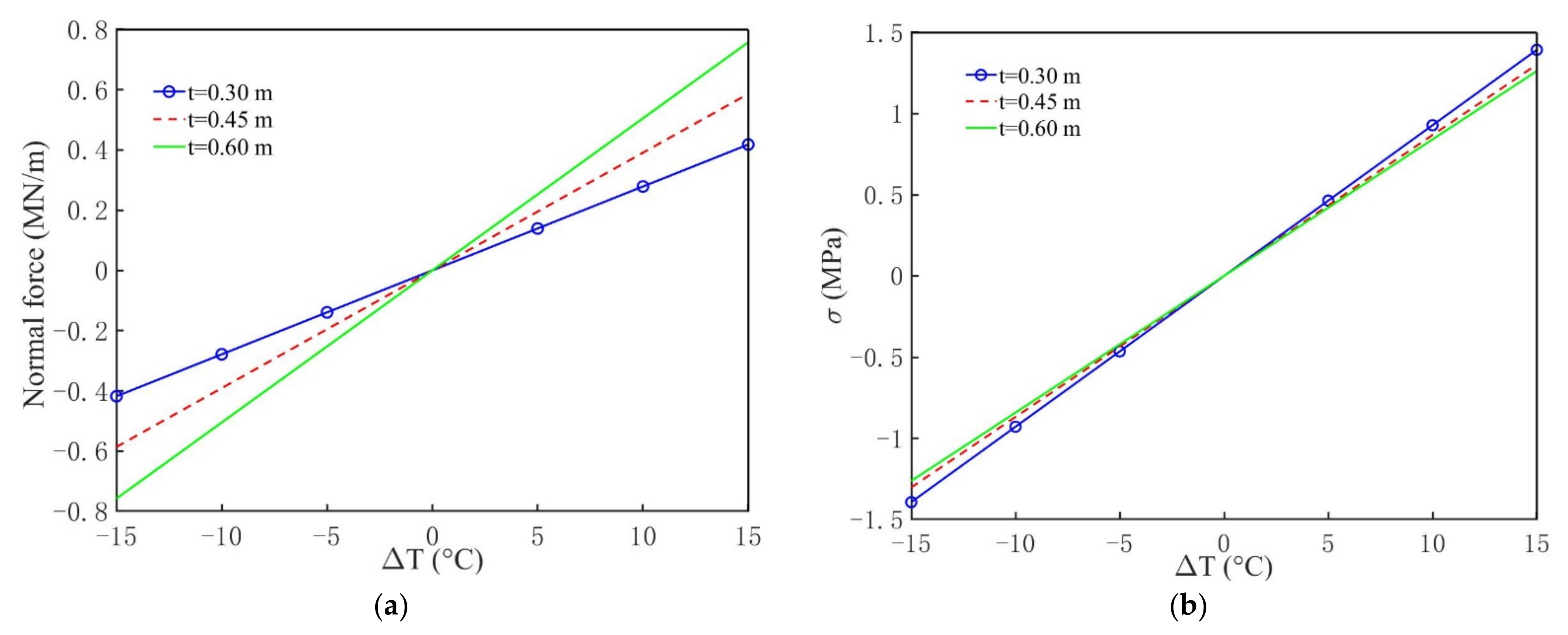
3.3.1. Impact of Lining Thickness t
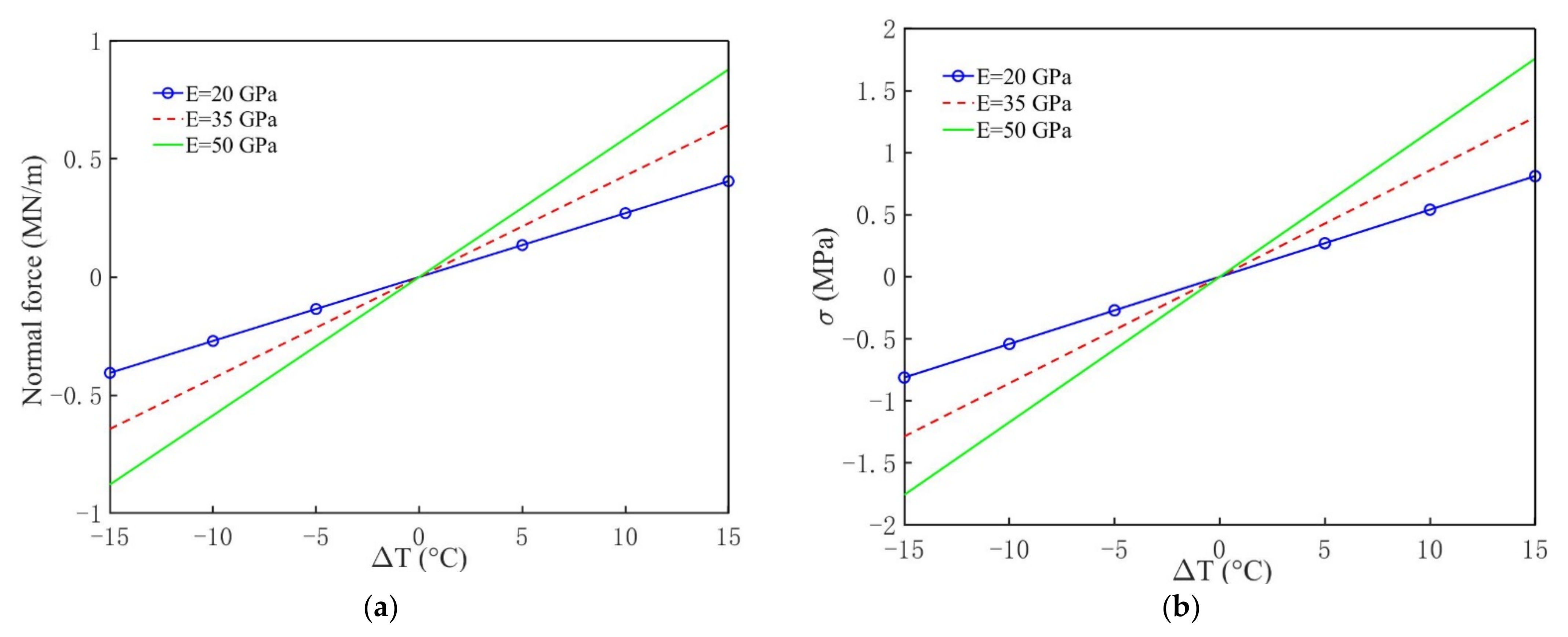
3.3.2. Impact of Lining Elastic Modulus E
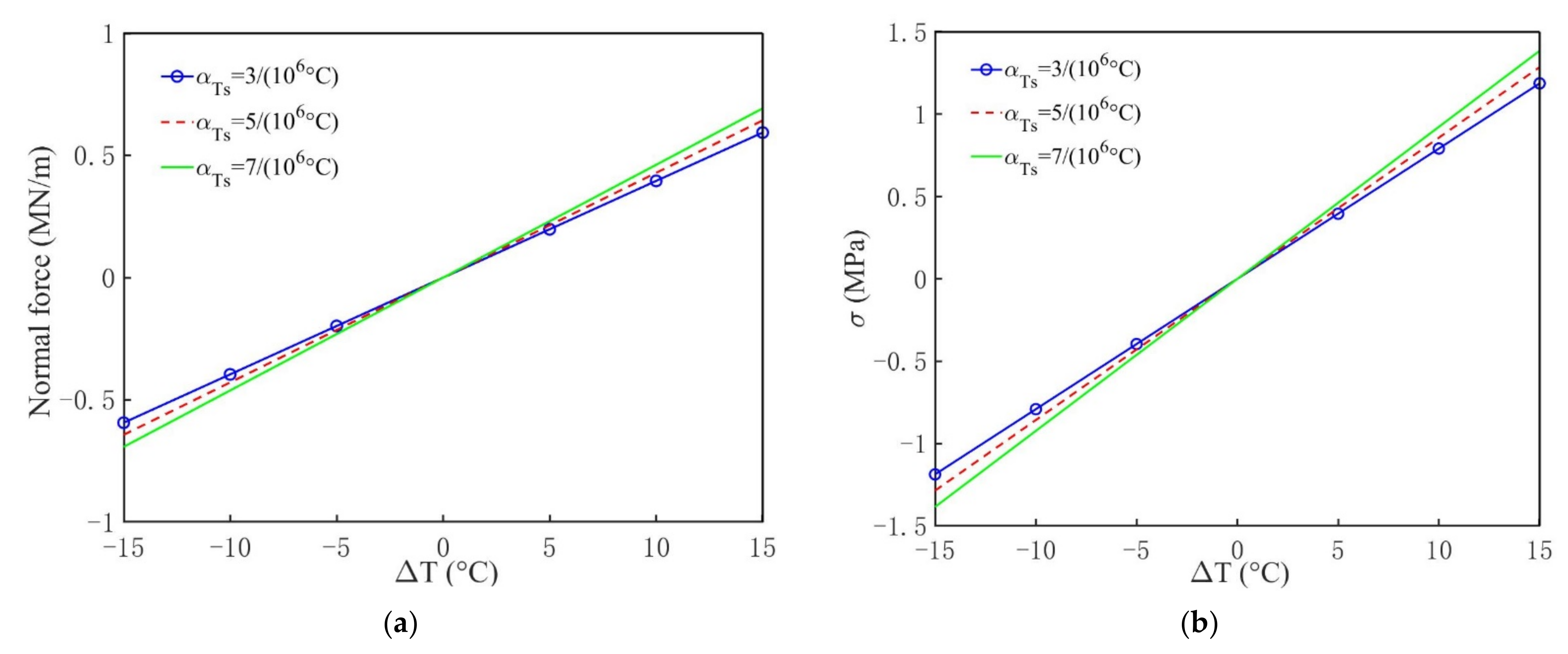
3.3.3. Impact of the Thermal Expansion Coefficient of the Ground
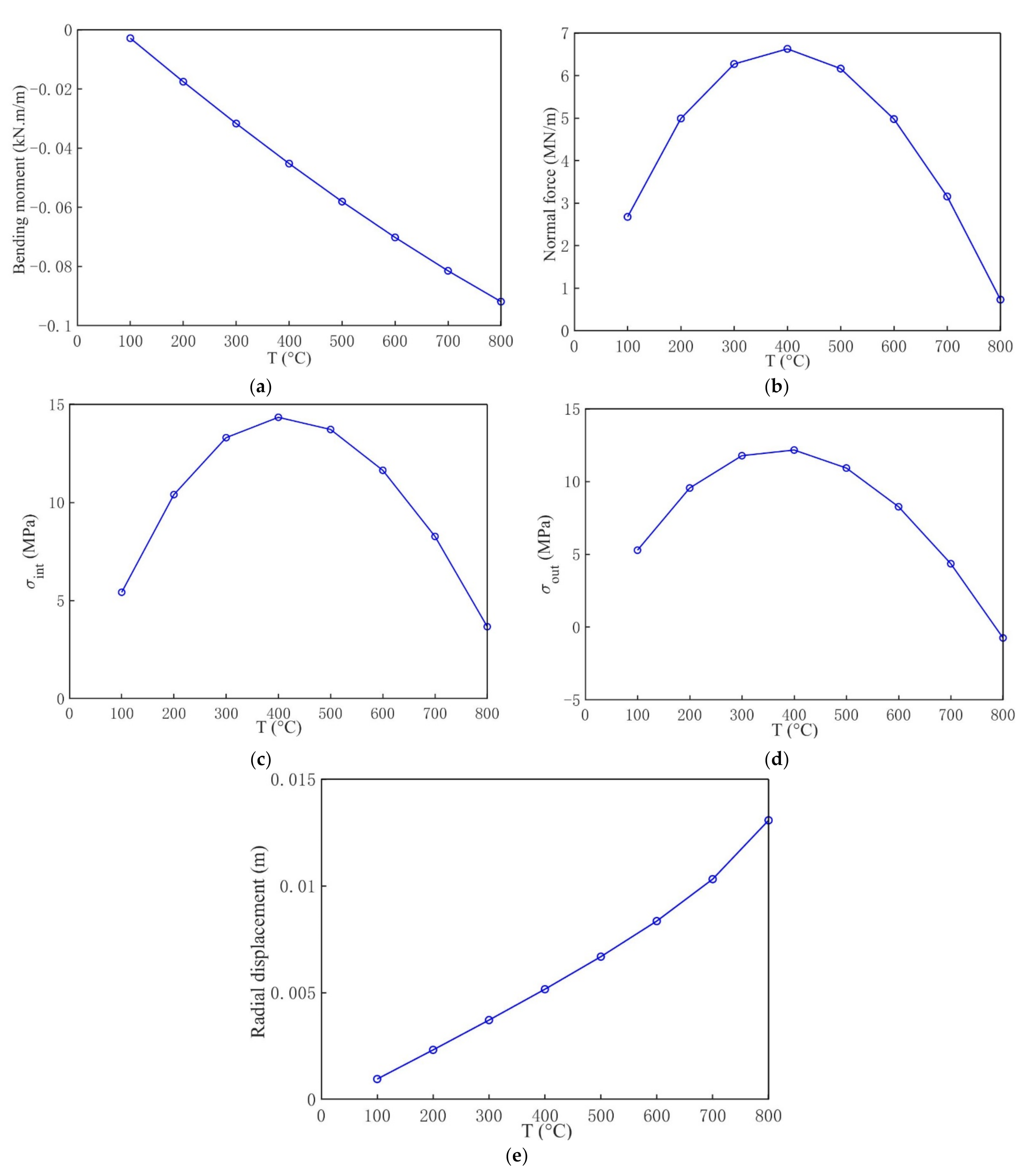
4. Impact of Fires on the Internal Forces of Tunnel Lining
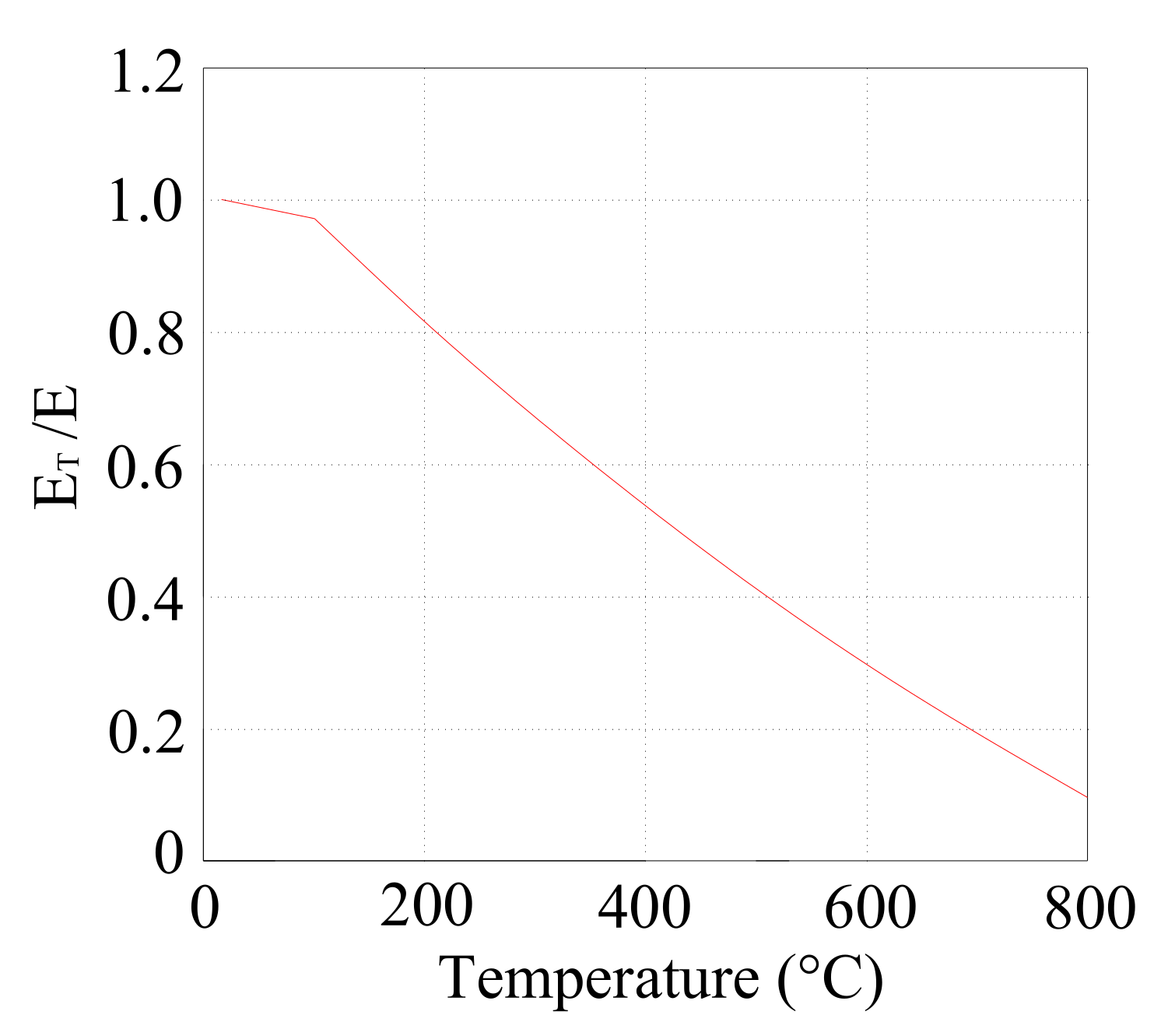
4.1. Impact of Fires on the Elastic Modulus E of Tunnel Lining
4.2. Impact of Fires on the Behavior of Tunnel Lining
5. Conclusions
- Heating the lining generates compressive forces, whereas cooling the lining leads to tensile forces;
- The stresses of tunnel lining decrease with the increase of lining thickness, whereas the absolute values of lining normal forces increase as the lining thickness increases;
- The absolute internal forces values of tunnel lining increase with the increase of the lining elastic modulus;
- The effect of the soil thermal expansion coefficient on the internal forces of tunnel lining could be neglected;
- The maximum force of tunnel lining appears when the temperature is about 400 °C for a fire event.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Luo, Y.B.; Chen, J.X.; Qiao, X.; Wang, M.S. Mechanics state analysis of secondary lining concrete structure on tunnel based on temperature effect. China J. Highw. Transp. 2010, 23, 64–69. [Google Scholar]
- Nicholson, D.P.; Chen, Q.; Silva, M.; Winter, A.; Winterling, R. The design of thermal tunnel energy segments for Crossrail, UK. Proc. Inst. Civ. Eng. Eng. Sustain. 2014, 167, 118–134. [Google Scholar] [CrossRef] [Green Version]
- Brandl, H. Energy foundations and other thermo-active ground structures. Géotechnique 2006, 56, 81–122. [Google Scholar] [CrossRef]
- Franzius, J.N.; Pralle, N. Turning segmental tunnels into sources of renewable energy. Proc. Inst. Civ. Eng. 2011, 164, 35. [Google Scholar] [CrossRef]
- Barla, M.; Perino, A. Energy from geo-structures: A topic of growing interest. Environ. Geotech. 2015, 2, 3–7. [Google Scholar] [CrossRef] [Green Version]
- Barla, M.; Di Donna, A.; Insana, A. A novel real-scale experimental prototype of energy tunnel. Tunn. Undergr. Space Technol. 2019, 87, 1–14. [Google Scholar] [CrossRef]
- Kaundinya, I. Protection of road tunnel linings in cases of fire. In Proceedings of the FEHRL/FERSI/ECTRI Young Researchers Seminar, Brno, Czech Republic, 28–30 May 2007. [Google Scholar]
- Maraveas, C.; Vrakas, A.A. Design of concrete tunnel linings for fire safety. Struct. Eng. Int. 2014, 24, 319–329. [Google Scholar] [CrossRef] [Green Version]
- Zeiml, M.; Lackner, R.; Mang, H.A. Experimental insight into spalling behaviour of concrete tunnel linings under fire loading. Acta Geothech. 2008, 3, 295–308. [Google Scholar] [CrossRef]
- Barla, M.; Di Donna, A. Energy tunnels: Concept and design aspects. Undergr. Space 2018, 3, 268–276. [Google Scholar] [CrossRef]
- Oreste, P.P. A numerical approach to the hyperstatic reaction method for the dimensioning of tunnel supports. Tunn. Undergr. Space Technol. 2007, 22, 185–205. [Google Scholar] [CrossRef]
- Do, N.A.; Dias, D.; Oreste, P.; Djeran-Maigre, I. The behaviour of the segmental tunnel lining studied by the hyperstatic reaction method. Eur. J. Environ. Civ. Eng. 2013, 18, 489–510. [Google Scholar] [CrossRef]
- Du, D.C.; Dias, D.; Do, N.A.; Oreste, P.P. Hyperstatic Reaction Method for the Design of U-Shaped Tunnel Supports. Int. J. Geomech. 2018, 18, 1–12. [Google Scholar] [CrossRef]
- Du, D.C.; Dias, D.; Do, N.A. Designing U-shaped tunnel linings in stratified soils using the hyperstatic reaction method. Eur. J. Environ. Civ. Eng. 2018, 11, 1–18. [Google Scholar] [CrossRef]
- Du, D.C.; Dias, D.; Yang, X.L. Analysis of earth pressure for shallow tunnels in anisotropic and non-homogeneous soil. Comput. Geotech. 2018, 104, 226–236. [Google Scholar] [CrossRef]
- Guo, X.F.; Du, D.C.; Dias, D. Reliability analysis of tunnel lining considering soil spatial variability. Eng. Struct. 2019, 196, 109332. [Google Scholar] [CrossRef]
- Du, D.C.; Dias, D.; Do, N.A. Lining performance optimization of sub-rectangular tunnels using the Hyperstatic Reaction Method. Comput. Geotech. 2020, 117, 103279. [Google Scholar] [CrossRef]
- Du, D.C.; Dias, D.; Do, N.A.; Vo, T. U-shaped tunnel lining design using the Hyperstatic Reaction Method—Influence of the invert. Soils Found. 2020, 60, 592–607. [Google Scholar] [CrossRef]
- Du, D.C.; Dias, D.; Do, N.A. Effect of surcharge loading on horseshoe-shaped tunnels excavated in saturated soft rocks. J. Rock Mech. Geotech. Eng. 2020, 12, 1339–1346. [Google Scholar] [CrossRef]
- Sun, Q.Q.; Du, D.C.; Dias, D. An improved Hyperstatic Reaction Method for tunnels under seismic loading. Tunn. Undergr. Space Technol. 2021, 108, 103687. [Google Scholar] [CrossRef]
- Arnau, O.; Molins, C. Experimental and analytical study of the structural response of segmental tunnel supports based on an in situ loading test. Part 2: Numerical simulation. Tunn. Undergr. Space Technol. 2010, 26, 778–788. [Google Scholar] [CrossRef] [Green Version]
- Xi, B.P.; Zhao, Y.S. Experimental study of thermo-physico-mechanical property of drilling surrounding rock in granite under high temperature and high pressure. Chin. J. Rock Mech. Eng. 2010, 29, 1245–1253. [Google Scholar]
- Takano, Y.H. Guidelines for the design of shield tunnel lining. Tunn. Undergr. Space Technol. 2000, 15, 303–331. [Google Scholar]
- Amatya, B.; Soga, K.; Bourne-Webb, P.J.; Amis, T.; Laloui, L. Thermo-mechanical behaviour of energy piles. Géotechnique 2012, 62, 503–519. [Google Scholar] [CrossRef]
- Oreste, P.P.; Dias, D. Stabilisation of the excavation face in shallow tunnels using fibreglass dowels. Rock Mech. Rock Eng. 2012, 45, 499–517. [Google Scholar] [CrossRef]
- Bourne-Webb, P.J.; Bodas-Freitas, T.M.; Freitas-Assunção, R.M. Soil–pile thermal interactions in energy foundations. Géotechnique 2015, 66, 167–171. [Google Scholar] [CrossRef]
- Aslani, F.; Samali, B. Constitutive relationships for steel fibre reinforced concrete at elevated temperatures. Fire Technol. 2014, 50, 1249–1268. [Google Scholar] [CrossRef]
- Hertz, K.D. Limits of spalling of fire-exposed concrete. Fire Saf. J. 2003, 38, 103–116. [Google Scholar] [CrossRef]
- Guo, J.; Jiang, S.P.; Zhang, Z.Y. Fire thermal stress and its damage to subsea immersed tunnel. Procedia Eng. 2016, 166, 296–306. [Google Scholar] [CrossRef]

| Lining Properties | Symbol | Value | Unit |
|---|---|---|---|
| Tunnel radius | R | 6.08 | m |
| Thickness of lining | t | 0.45 | m |
| Poisson’s ratio of lining | v | 0.16 | - |
| Elastic Modulus of lining | E | 2.95 × 104 | MPa |
| Coefficient of thermal expansion | 9 × 10−6 | °C−1 |
| Temperature Change ∆T (°C) | Normal Force N (kN/m) | ||
|---|---|---|---|
| Luo et al. [1] | Present Method | Error | |
| −10.1 | 207.45 | 192.99 | 6.97% |
| −11.6 | 222.53 | 221.66 | 0.39% |
| Symbol | Value | Unit | |
|---|---|---|---|
| Properties of lining | |||
| Tunnel radius | R | 6.02 | m |
| Thickness of lining | t | 0.50 | m |
| Poisson’s ratio of lining | v | 0.15 | - |
| Elastic Modulus of lining | E | 3.5 × 104 | MPa |
| Coefficient of thermal expansion | 1.2 × 10−5 | °C−1 | |
| Overburden thickness | h | 40 | m |
| Properties of ground | |||
| Elastic Modulus of ground | Es | 300 | MPa |
| Cohesion of ground | c | 50 | kPa |
| Internal friction angle | φ | 20 | degree |
| Unit weight of ground | γs | 22 | kN/m3 |
| Poisson’s ratio of ground | vs | 0.30 | - |
| Lateral earth pressure factor | K0 | 0.8 | - |
| Coefficient of thermal expansion | 5 × 10−6 | °C−1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, D.; Dias, D.; Do, N.-A. A Simplified Way to Evaluate the Effect of Temperature on a Circular Tunnel. Geotechnics 2021, 1, 385-401. https://doi.org/10.3390/geotechnics1020018
Du D, Dias D, Do N-A. A Simplified Way to Evaluate the Effect of Temperature on a Circular Tunnel. Geotechnics. 2021; 1(2):385-401. https://doi.org/10.3390/geotechnics1020018
Chicago/Turabian StyleDu, Dianchun, Daniel Dias, and Ngoc-Anh Do. 2021. "A Simplified Way to Evaluate the Effect of Temperature on a Circular Tunnel" Geotechnics 1, no. 2: 385-401. https://doi.org/10.3390/geotechnics1020018
APA StyleDu, D., Dias, D., & Do, N.-A. (2021). A Simplified Way to Evaluate the Effect of Temperature on a Circular Tunnel. Geotechnics, 1(2), 385-401. https://doi.org/10.3390/geotechnics1020018








