A New Load-Transfer Factor to the Slipping Analytical Formulation in Axially Loaded Piles
Abstract
:1. Introduction
2. Background
2.1. Load-Transfer Factor (ζ)
2.2. Pile–Soil Interface
3. A Review of the Load-Transfer Factor by Finite Element Analysis
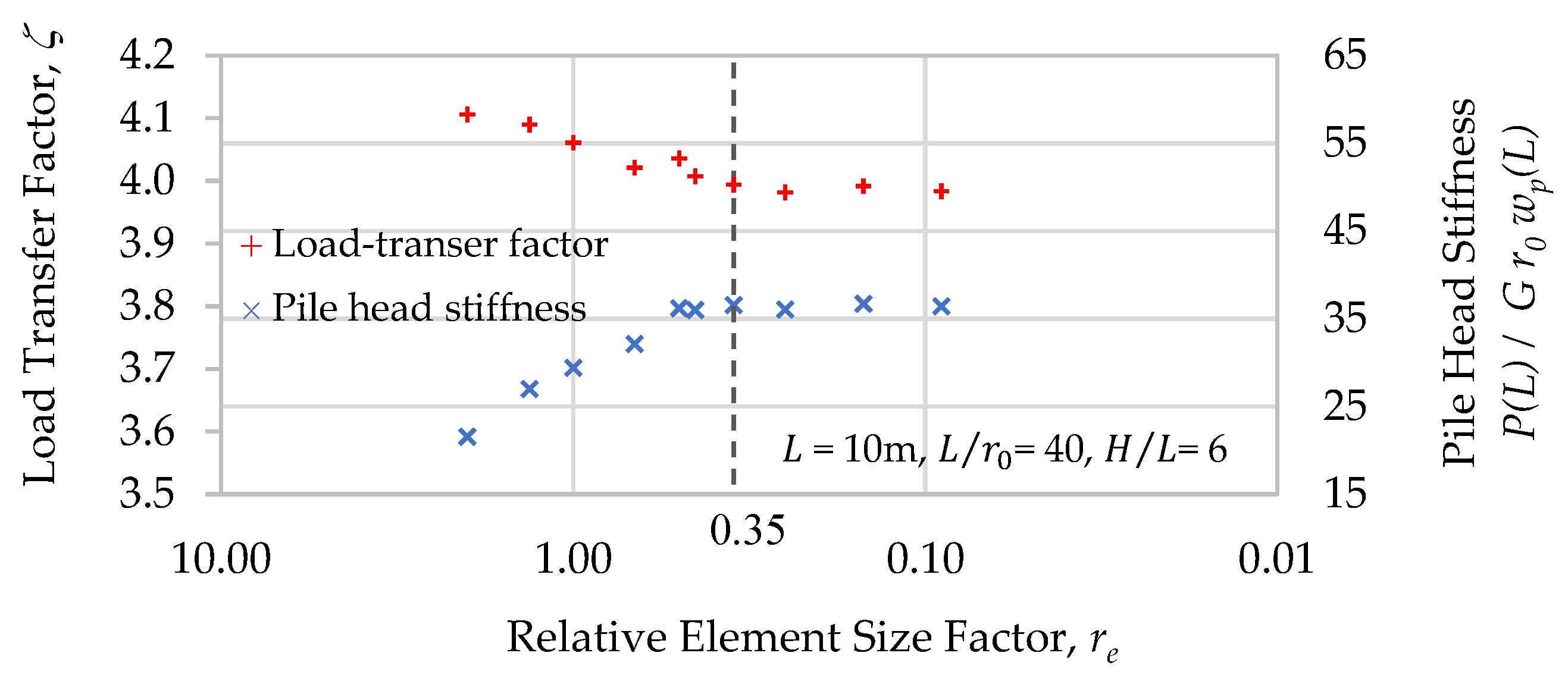
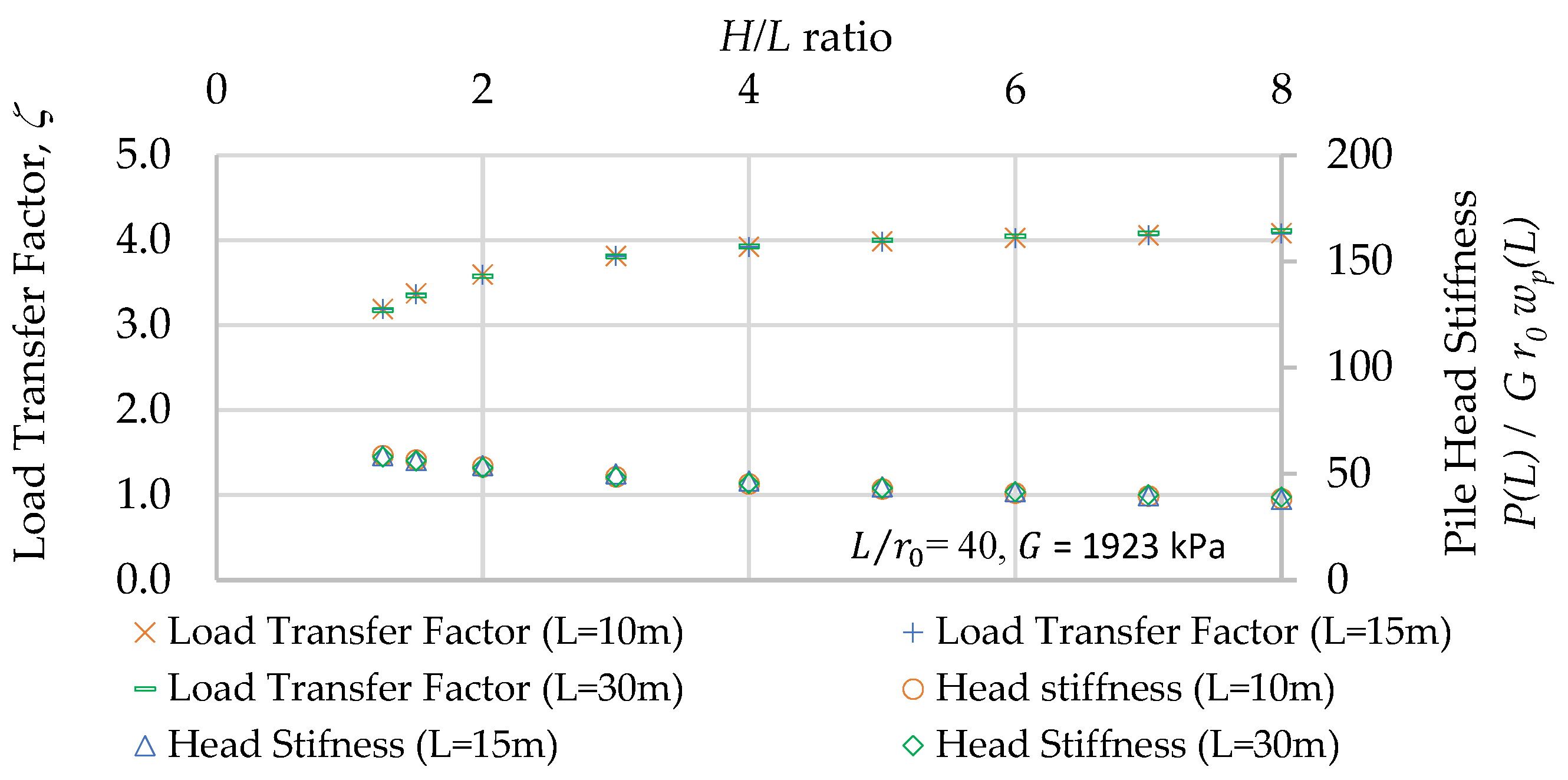
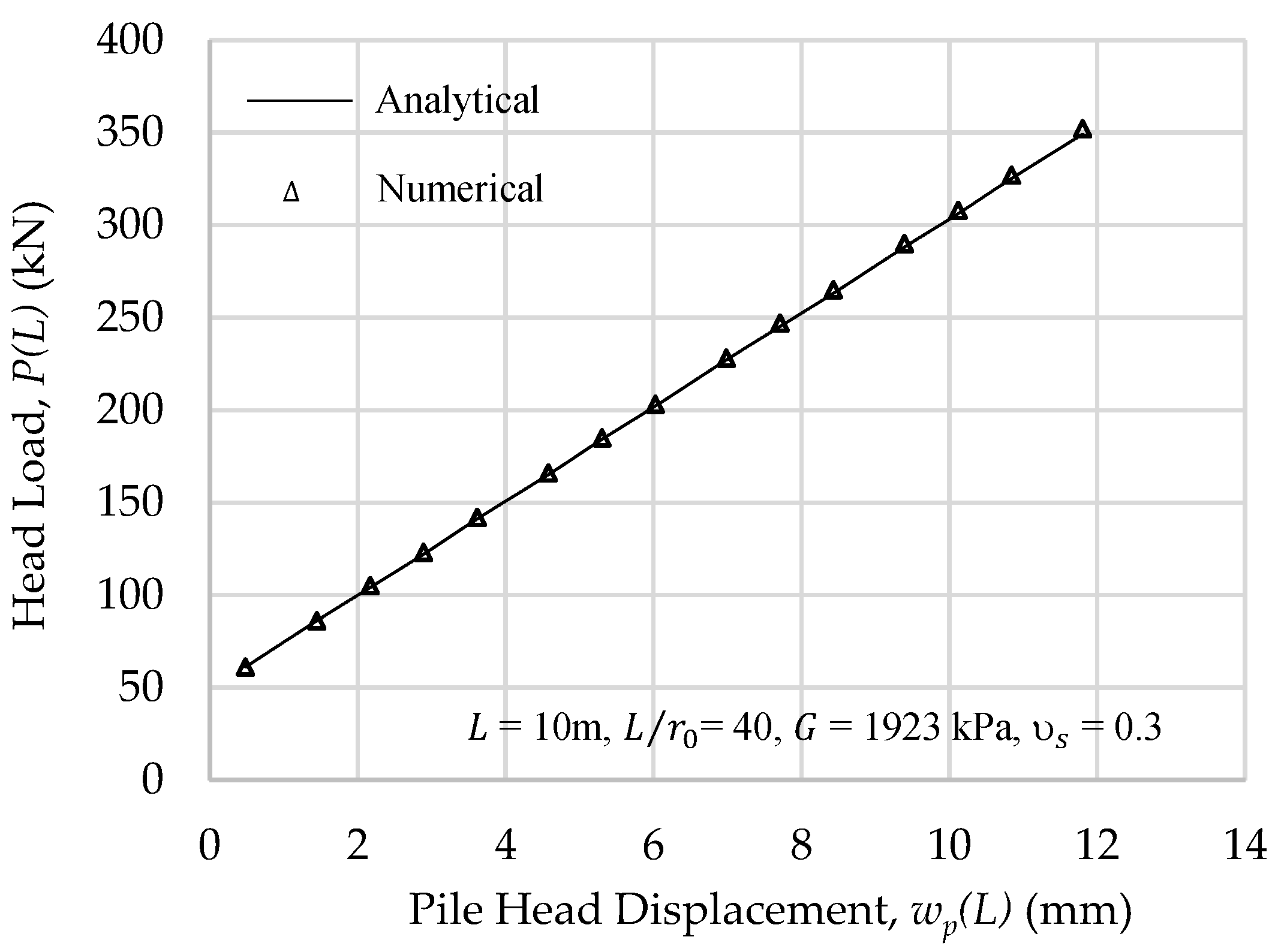
3.1. Model Verification
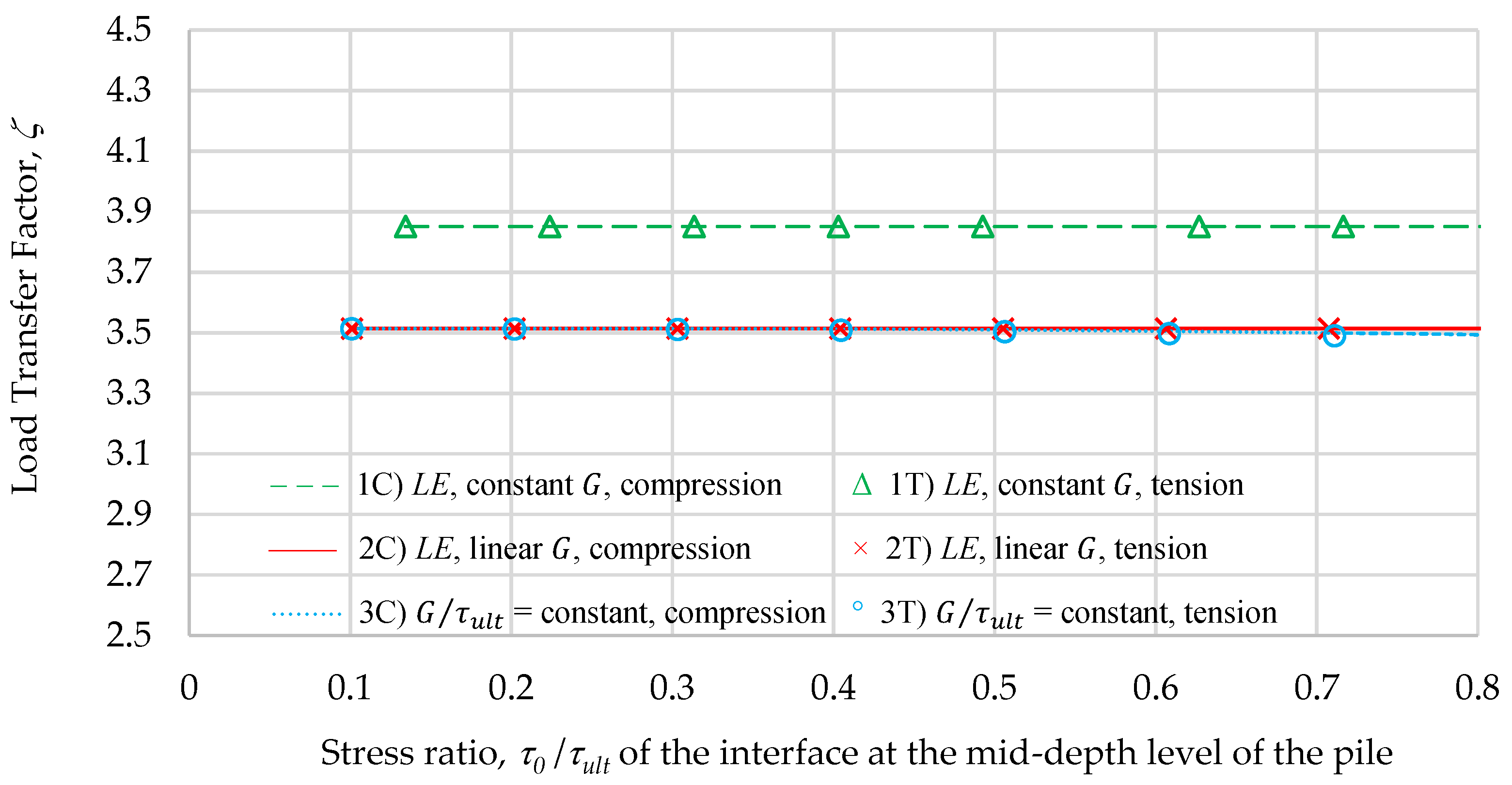
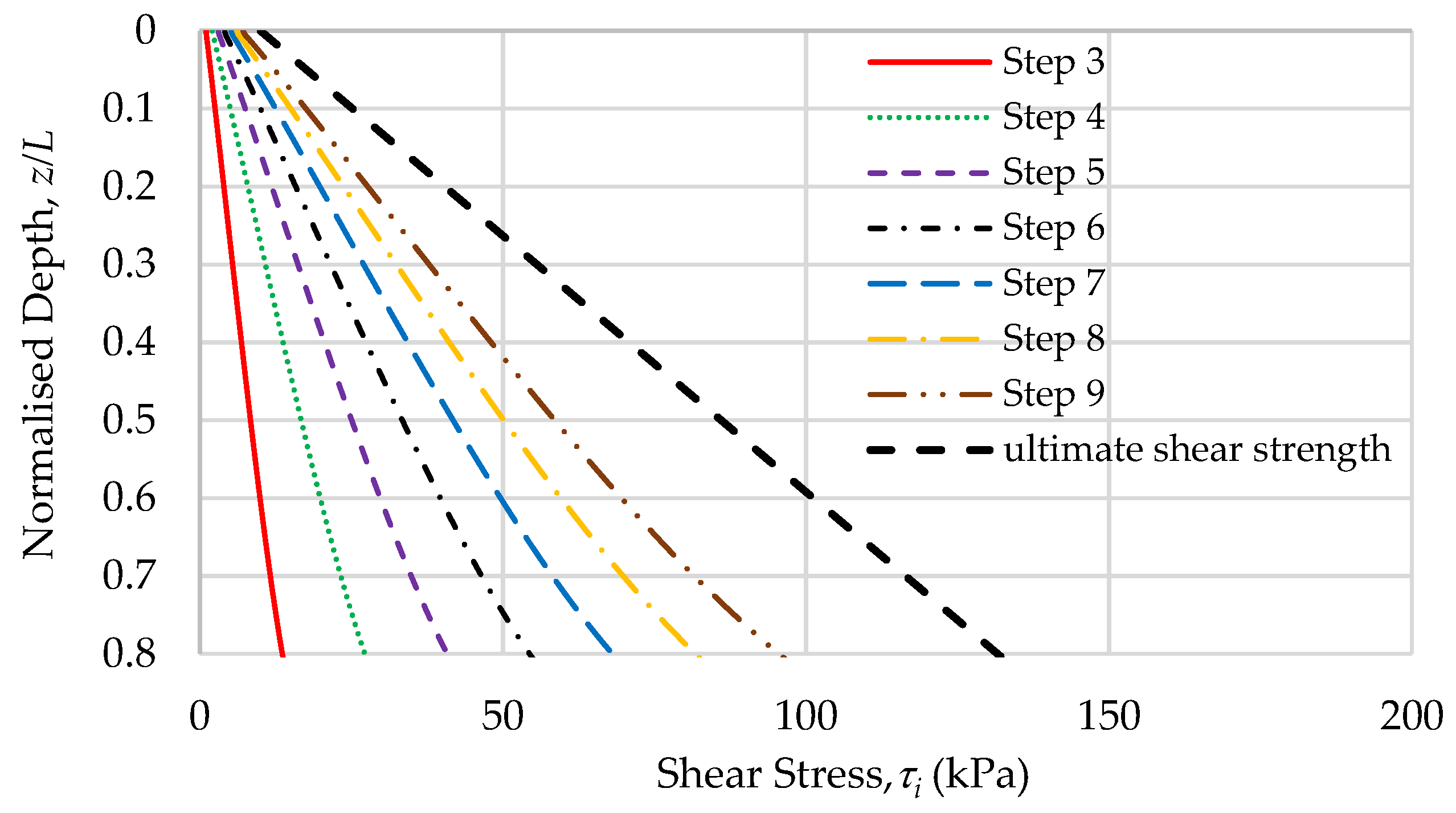
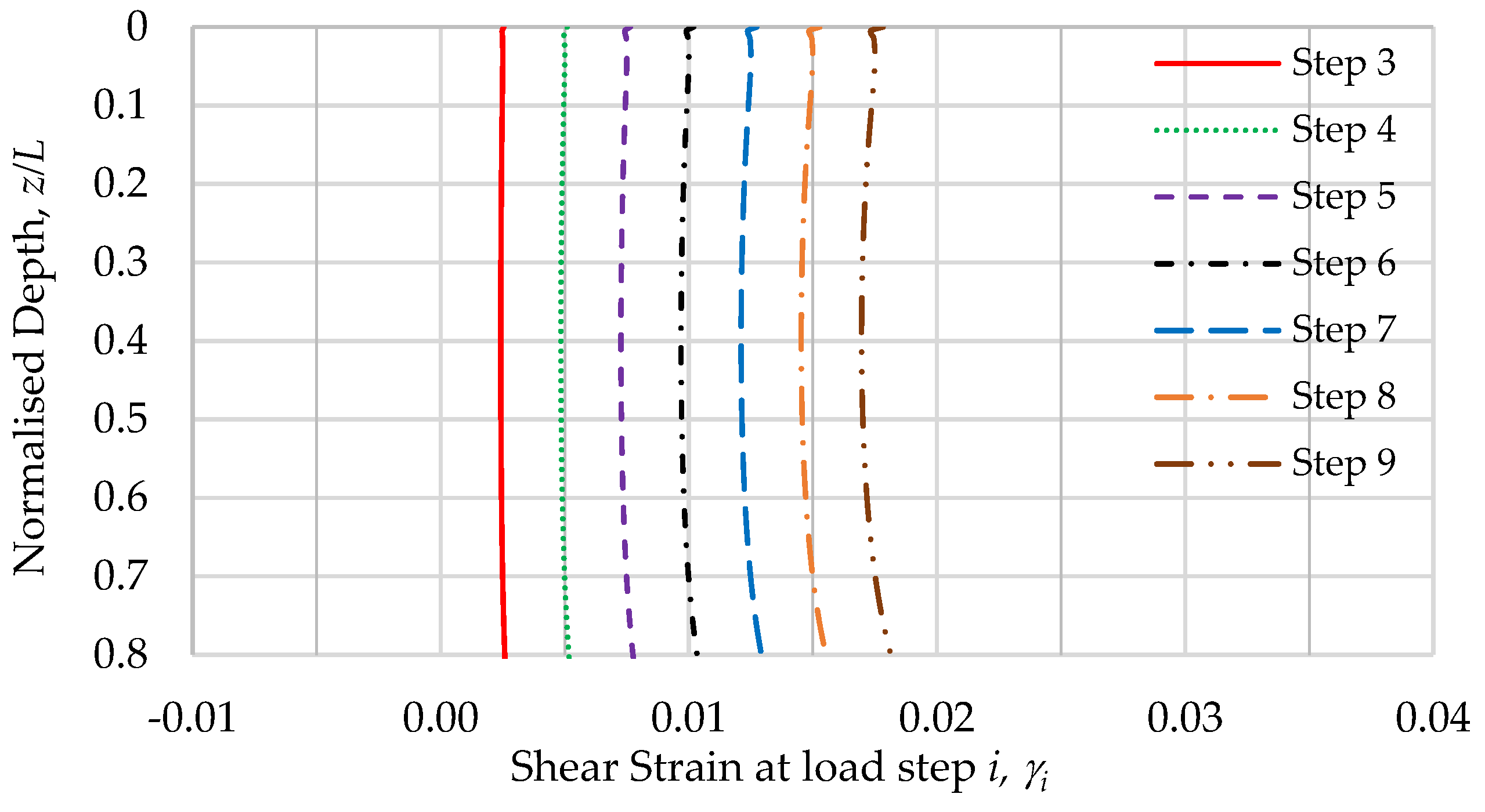
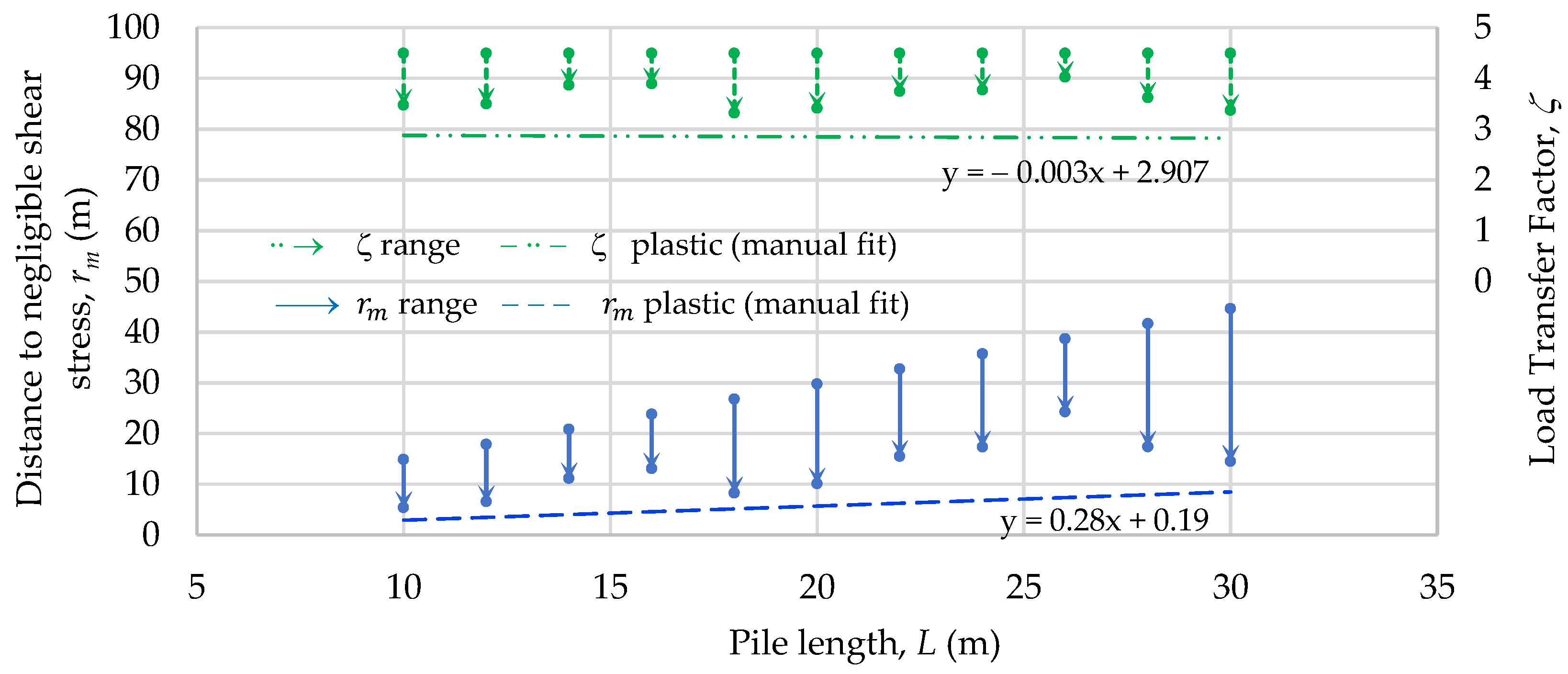
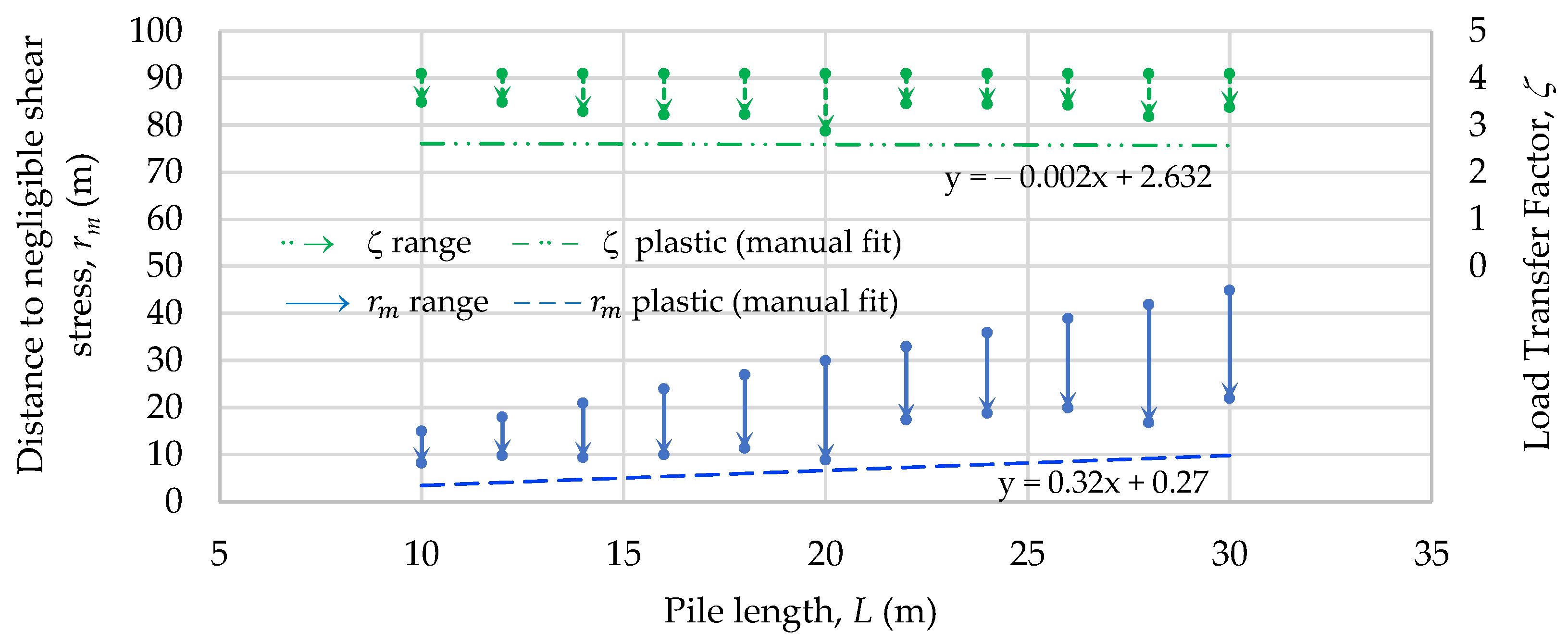
3.2. A Review of the Load-Transfer Factor
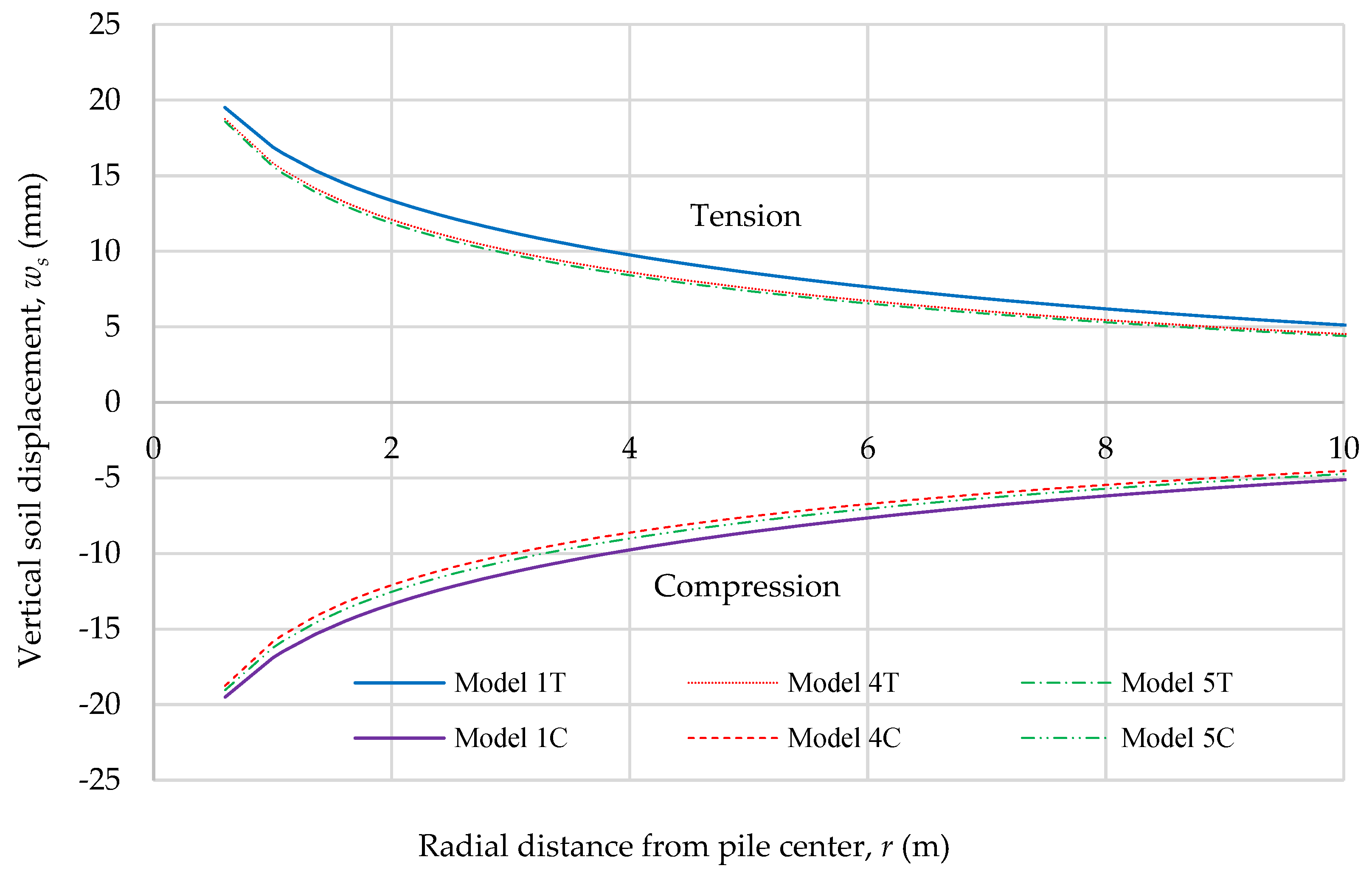
- Model 1: Homogeneous, LE constitutive soil model.
- Model 2: Gibson (inhomogeneous), LE constitutive soil model.
- Model 3: Gibson (inhomogeneous), elastoplastic MC constitutive soil model with a constant ratio where the entire pile–soil interface becomes plastic (reaching the ultimate shear strength, ) along the total pile length simultaneously.
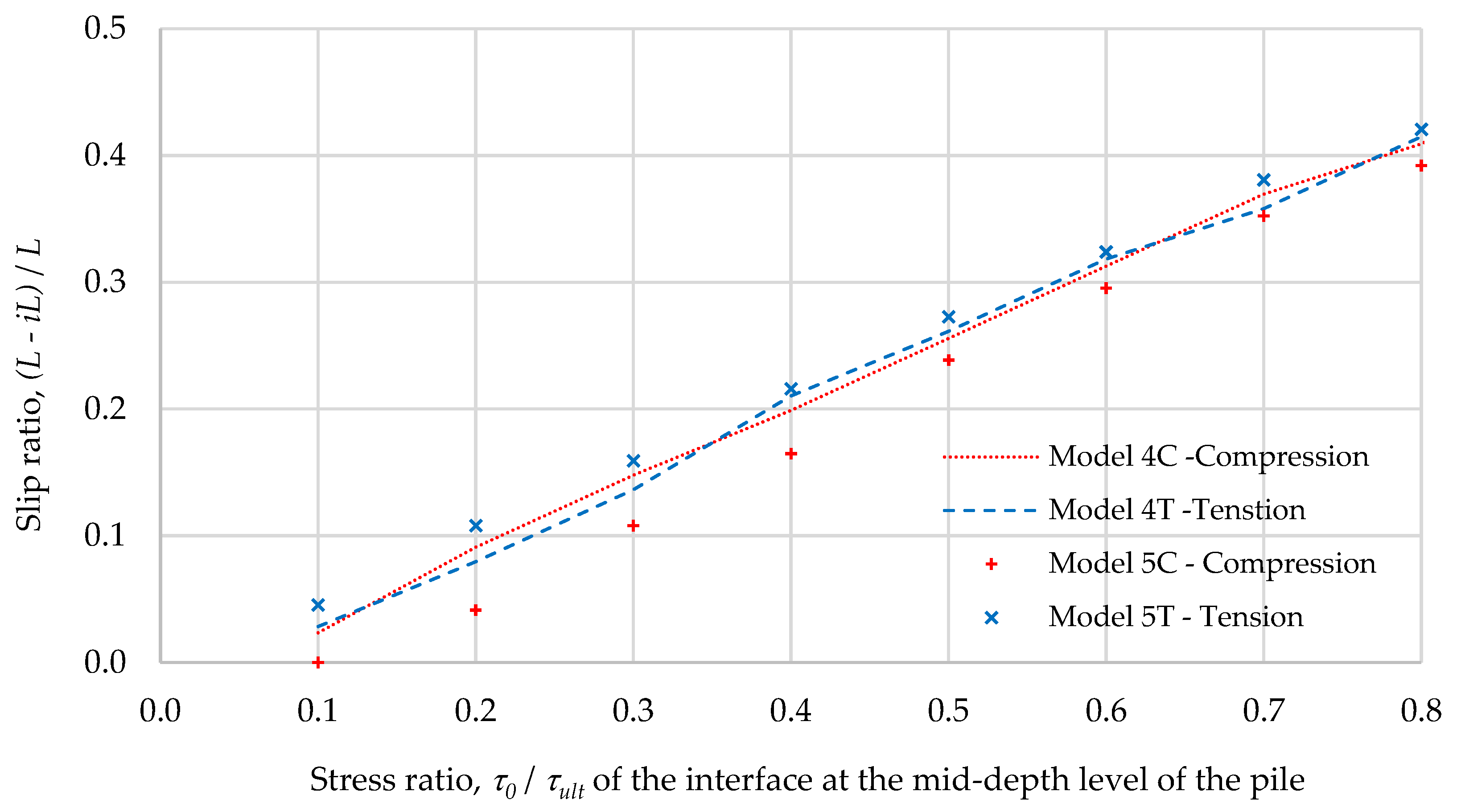
- Model 4: Homogenous (modulus only), MC constitutive soil model with a fixed strength profile along the interface. The shear strength profile is an input parameter converted from initial overburden stress based on Das [23] to simulate cohesionless soil. It is a simplified version of Model 5.
- Model 5: Homogenous (modulus only), MC constitutive soil model with a variable strength profile along the interface. Soil strength is a function of the friction angle (input parameter) and the rotation of principal stresses (updated automatically as pile-head load increases).
4. New Analytical Method and Improvement in the Load–Displacement Curve
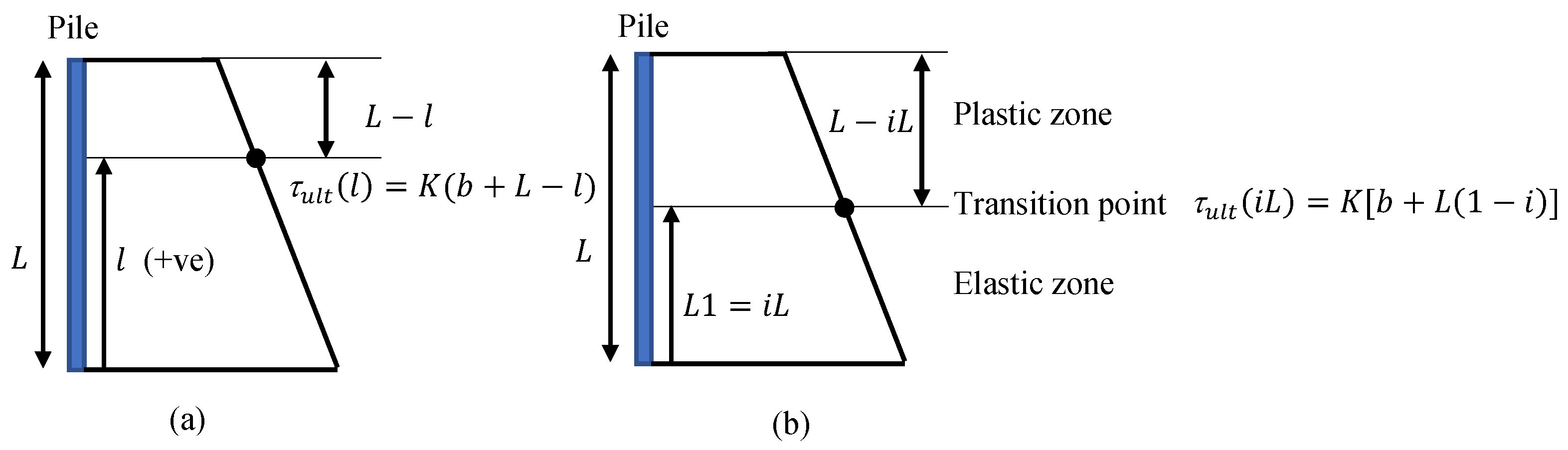
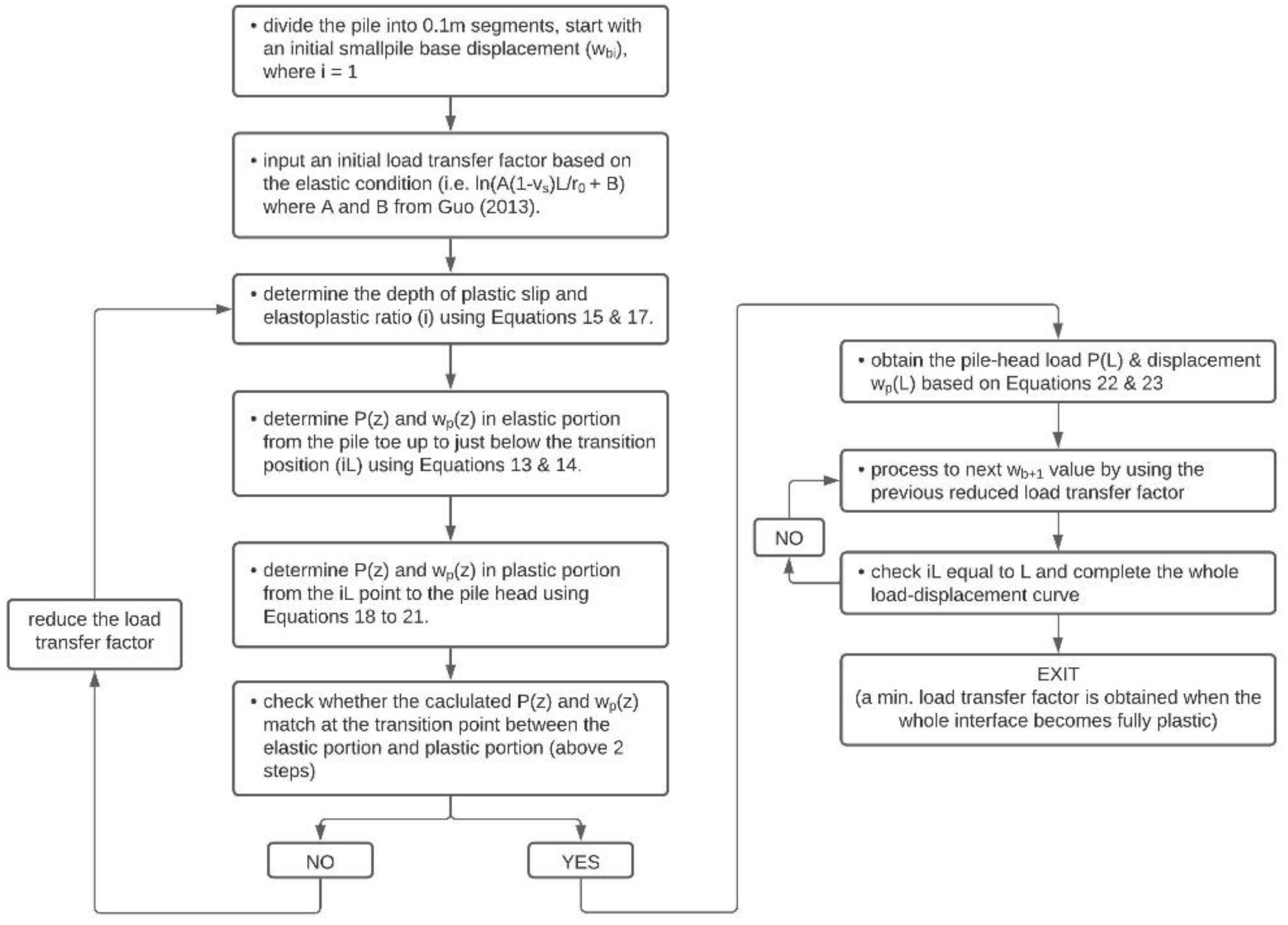
4.1. Devising the Elastoplastic Analytical Solution
4.1.1. Elastic Component
4.1.2. Plastic Component
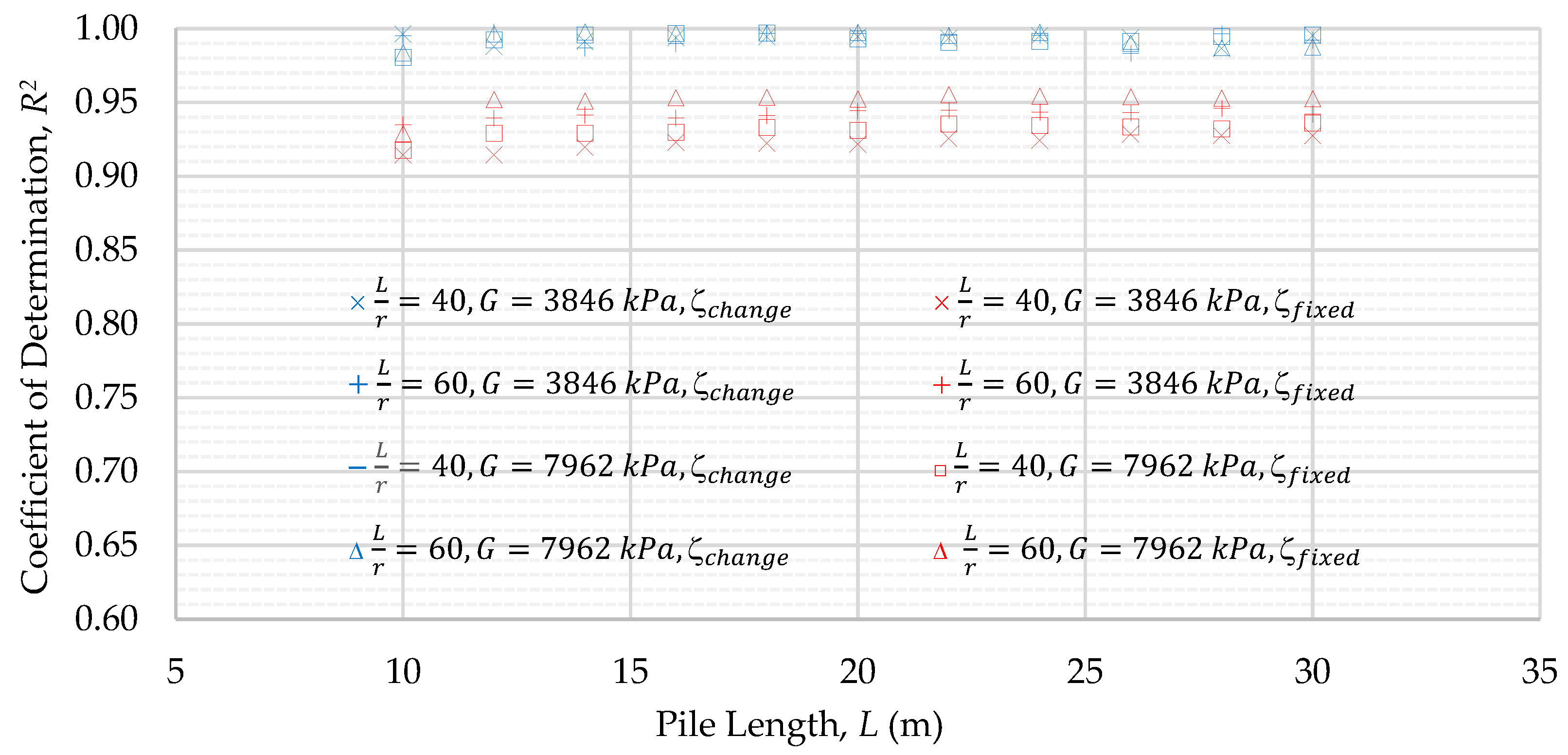
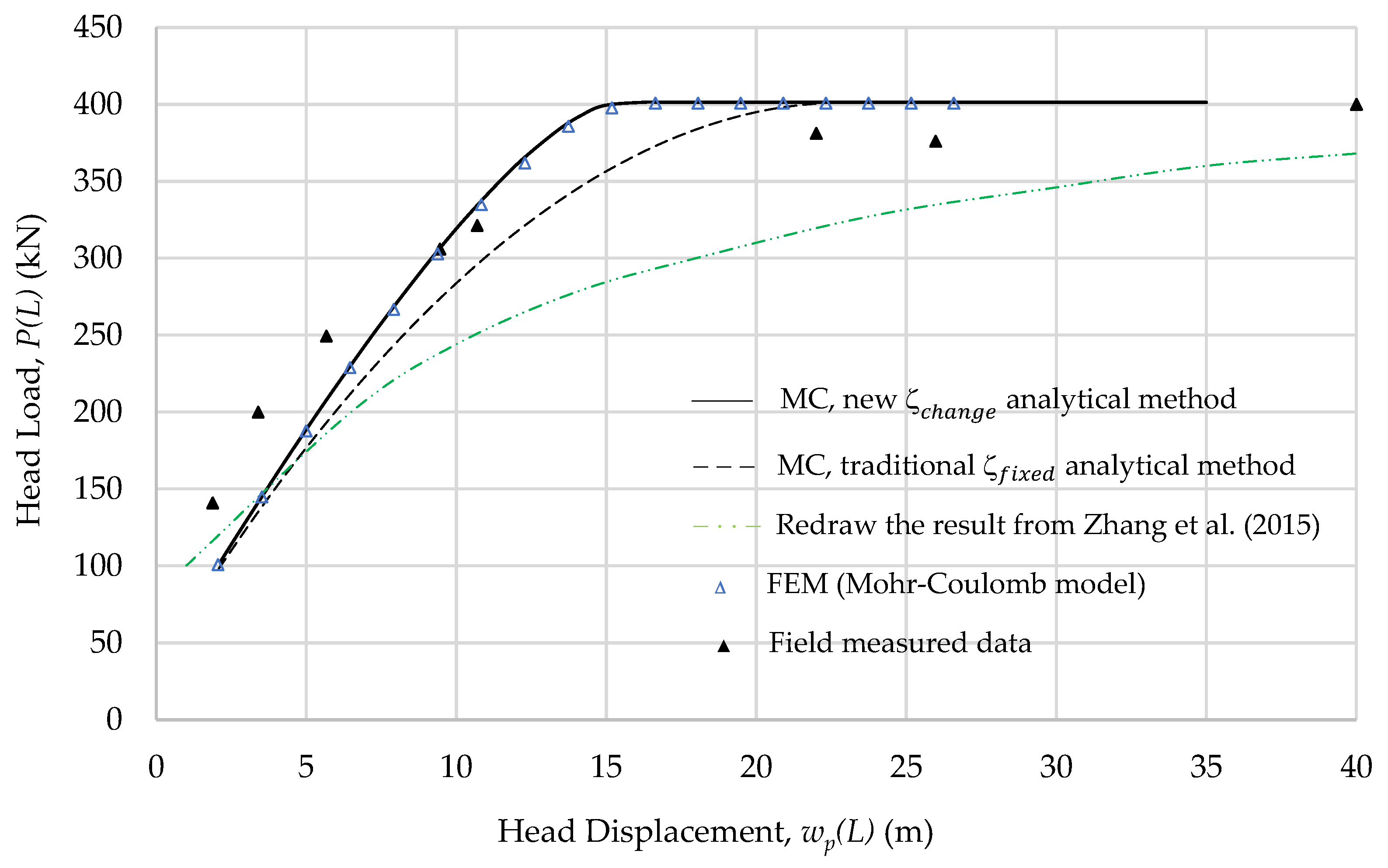
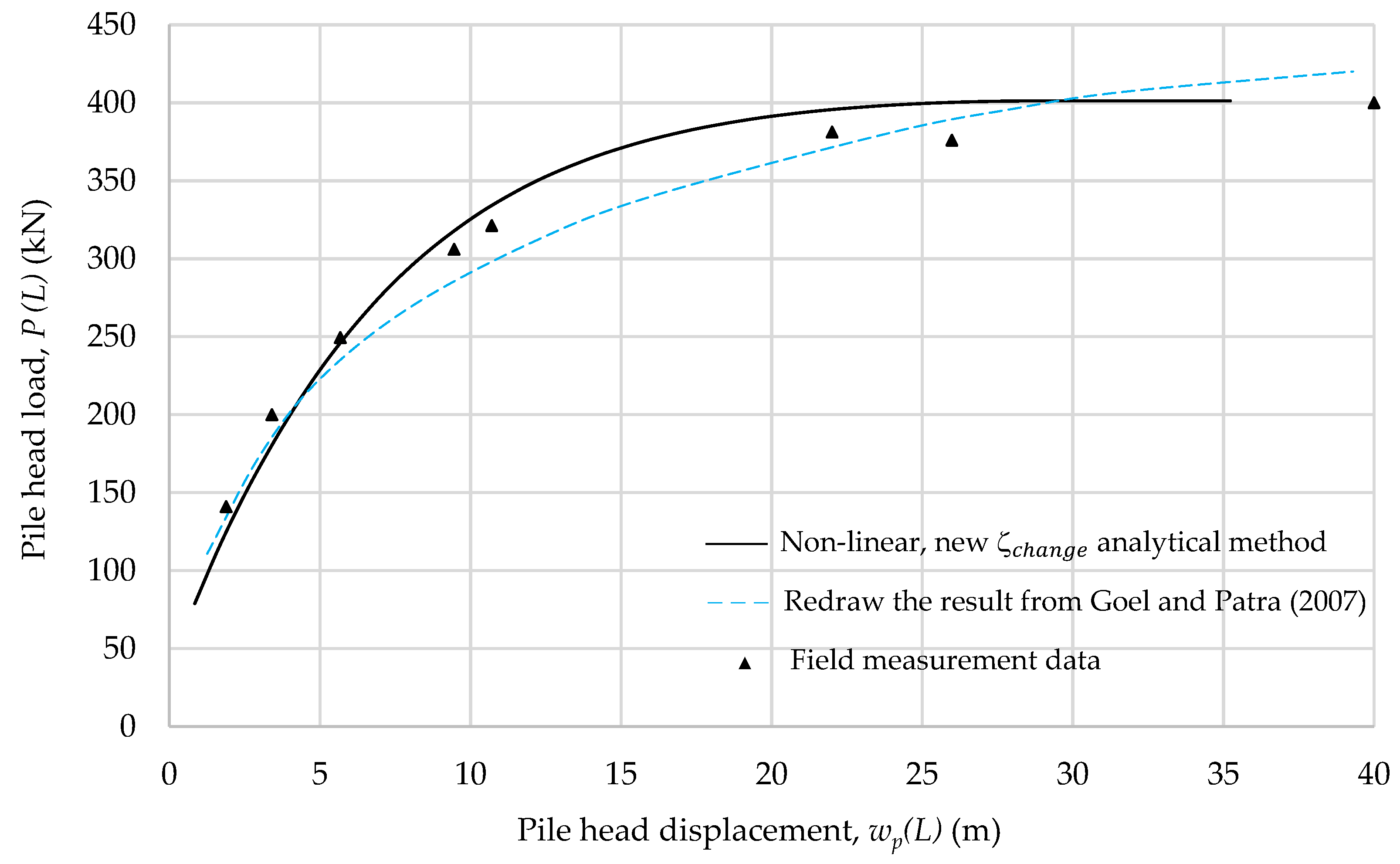
4.2. Improvement in the Load–Displacement Curve at the Pile Head by the New Analytical Method
4.3. Application to a Case Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Randolph, M.F.; Wroth, C.P. Analysis of deformation of vertically loaded piles. J. Geotech. Geoenviron.Eng. 1978, 104, 1465–1488. [Google Scholar] [CrossRef]
- Kraft, L.M.; Ray, R.P.; Kagawa, T. Theoretical t-z curves. J. Geotech. Geoenviron. Eng. 1981, 107, 1543–1561. [Google Scholar] [CrossRef]
- Alawneh, A.S. Modelling load-displacement response of driven piles in cohesionless soils under tensile loading. Comput. Geotech. 2005, 32, 578–586. [Google Scholar] [CrossRef]
- Pando, M.A.; Ealy, C.D.; Filz, G.M.; Lesko, J.J.; Hoppe, E.J. A Laboratory and Field Study of Composite Piles for Bridge Substructures; Federal Highway Administration, United States: Washington, DC, USA, 2006.
- Wang, Z.; Xie, X.; Wang, J. A new nonlinear method for vertical settlement prediction of a single pile and pile groups in layered soils. Comput. Geotech. 2012, 45, 118–126. [Google Scholar] [CrossRef]
- Zhang, Q.Q.; Li, S.C.; Zhang, Z.M. Influence of reaction piles on test pile response in a static load test. J. Zhejiang Univ. Sci. A 2013, 14, 198–205. [Google Scholar] [CrossRef] [Green Version]
- Cheng, S.; Zhang, Q.Q.; Li, S.C.; Li, L.P.; Zhang, S.M.; Wang, K. Nonlinear analysis of the response of a single pile subjected to tension load using a hyperbolic model. Eur. J. Environ. Civ. Eng. 2018, 22, 181–191. [Google Scholar] [CrossRef]
- Lo, K.; Newell, D.; Oh, E. Comparing analytical models with slipping and non-slipping interface in axially loaded tension piles. In Proceedings of the 45th Annual Conference on Deep Foundations Institute, Online Conference, 27–30 October 2020. [Google Scholar]
- Sheil, B.B.; McCabe, B.A. An analytical approach for the prediction of single pile and pile group behaviour in clay. Comput. Geotech. 2016, 75, 145–158. [Google Scholar] [CrossRef]
- Boonyatee, T.; Lai, Q.V. A non-linear load transfer method for determining the settlement of piles under vertical loading. Int. J. Geotech. Eng. 2017, 14, 206–217. [Google Scholar] [CrossRef]
- Randolph, M.F. Design methods for pile group and piled rafts. In Proceedings of the 13th International Conference of Soil Mechanics and Foundation Engineering, New Delhi, India, 5–10 January 1994; pp. 61–82. [Google Scholar]
- Poulos, H.G.; Davis, E.H. Pile Foundation Analysis and Design; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1980. [Google Scholar]
- Carter, J.P.; Kulhawy, F.H. Analysis and Design of Drilled Shaft Foundations Socketed into Rock; Electric Power Research Inst.: Palo Alto, CA, USA; Cornell Univ.: Ithaca, NY, USA, 1988; pp. 1943–1944. [Google Scholar]
- Guo, W.D. Theory and Practice of Pile Foundations; Taylor & Francis Group: New York, NY, USA, 2013. [Google Scholar]
- De Gennaro, V.; Frank, R.; Said, I. Finite element analysis of model piles axially loaded in sands. Riv. Ital. Geotech. 2008, 2, 44–62. [Google Scholar]
- Boulon, M. Basic features of soil structure interface behaviour. Comput. Geotech. 1989, 7, 115–131. [Google Scholar] [CrossRef]
- Selvadurai, A.P.S. Boundary element modelling of geomaterial interfaces. In Mechanics of Geomaterial Interfaces; Selvadurai, A.P.S., Boulon, M.J.B., Eds.; Elsevier: Amsterdam, The Netherlands, 1995; Volume 42, pp. 173–197. [Google Scholar]
- Coutinho, A.L.G.A.; Martins, M.A.D.; Sydenstricker, R.M.; Alves, J.L.D.; Landau, L. Simple zero thickness kinematically consistent interface elements. Comput. Geotech. 2003, 30, 347–374. [Google Scholar] [CrossRef]
- Reddy, E.S.; Chapman, D.N.; Sastry, V. Direct shear interface test for shaft capacity of piles in sand. Geotech. Test. J. 2000, 23, 199–205. [Google Scholar]
- Damians, I.P.; Yub, Y.; Lloret, A.; Bathurst, R.J.; Josa, A. Equivalent interface properties to model soil-facing interactions with zero-thickness and continuum element methodologies. In Proceedings of the 15th Pan-American Conference on Soil Mechanics and Geotechnical Engineering, Buenos Aires, Argentina, 15–18 November 2015; pp. 1065–1072. [Google Scholar]
- Wu, J.J.; Li, Y.; Cheng, Q.G.; Wen, H.; Liang, X. A simplified method for the determination of vertically loaded pile-soil interface parameters in layered soil based on FLAC 3D. Front. Struct. Civ. Eng. 2016, 10, 103–111. [Google Scholar] [CrossRef]
- PLAXIS 2D. PLAXIS 2D Reference Manual CONNECT Edition V20; Plaxis bv, Bentley System, Inc.: Delft, The Netherlands, 2019. [Google Scholar]
- Das, B.M. Uplift capacity of piles and pile groups in sand. In Proceedings of the Oceans’ 86, Washington, DC, USA, 22 January 1999; pp. 90–95. [Google Scholar]
- O’Neill, M.W. Side resistance in piles and drilled shafts. J. Geotech. Geoenviron. Eng. 2001, 127, 3–16. [Google Scholar] [CrossRef]
- De Nicola, A.; Randolph, M.F. Tensile and compressive shaft capacity of piles in sand. J. Geotech. Eng. 1993, 119, 1952–1973. [Google Scholar] [CrossRef]
- Misra, A.; Chen, C.H.; Oberoi, R.; Kleiber, A. Simplified analysis method for micropile pullout behavior. J. Geotech. Geoenviron. Eng. 2004, 130, 1024–1033. [Google Scholar] [CrossRef]
- Meerdink, L.A. Performance of Micropiles under Axial Tensile Loading. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2013. [Google Scholar]
- Sowa, V.A. Pulling capacity of concrete cast in situ bored piles. Can. Geotech. J. 1970, 7, 482–493. [Google Scholar] [CrossRef]
- Zhang, Q.Q.; Li, S.C.; Zhang, Q.; Li, L.P.; Zhang, B. Analysis on response of a single pile subjected to tension load using a softening model and a hyperbolic model. Mar. Georesour. Geotechnol. 2015, 33, 167–176. [Google Scholar] [CrossRef]

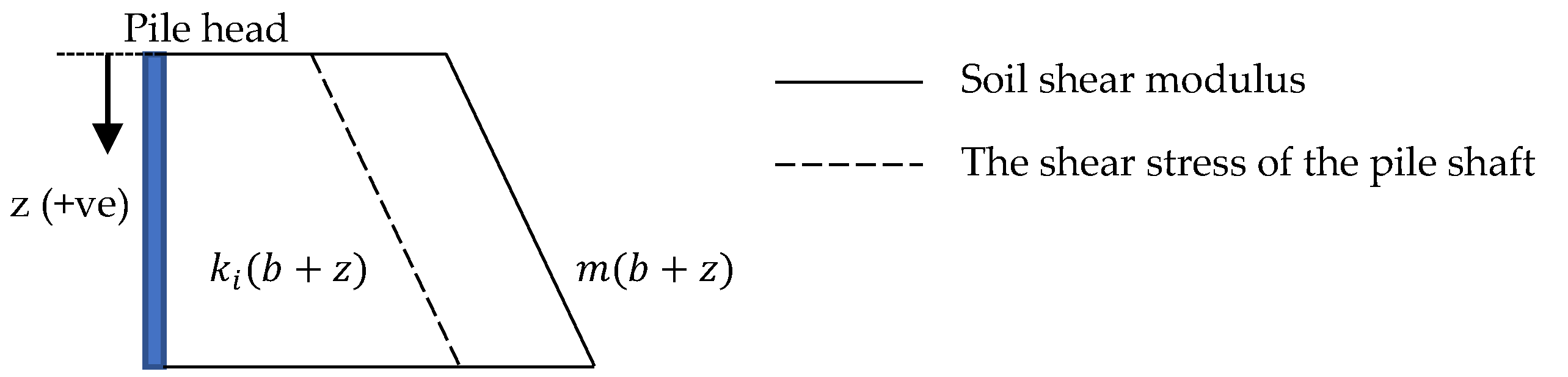






| Literature | A | B |
|---|---|---|
| (i) Randolph and Wroth [1] | 2.5 | 0 |
| (ii) Randolph [11] | 2.5 | 5 |
| (iii) Guo [14] A | 2.1 | 1 |
| MODEL | 1C/1T | 2C/2T | 3C/3T | 4C/4T | 5C/5T |
|---|---|---|---|---|---|
| Soil model | LE | LE | MC | MC | MC |
| (kPa) | 10,000 | 4000 | 4000 | 10,000 | 10,000 |
| (kPa/m) | 0 | 400 | 400 | 0 | 0 |
| (kPa) | - | - | 10 | 1 | 1 |
| (kPa/m) | - | - | 1 | 5.2 | - |
| (°) | - | - | - | - | 30 |
| At Head | Numerical | Proposed (Case 1) | Case 2—i | Case 2—ii | Case 2—iii |
|---|---|---|---|---|---|
| 8746 kN | +0.5% | −10.2 % | −11.0% | −8.3% | |
| 54.6 mm | −0.8% | +18.4% | +20.0% | +14.7% |
| (m) | G (MPa) | |||
|---|---|---|---|---|
| 10, 20, 30 | 20, 40, 60, 80 | 0.2, 0.3, 0.4 | 5, 10, 20 | 2, 6, 15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lo, K.; Oh, E.; Newell, D.; Yong, C. A New Load-Transfer Factor to the Slipping Analytical Formulation in Axially Loaded Piles. Geotechnics 2022, 2, 171-190. https://doi.org/10.3390/geotechnics2010008
Lo K, Oh E, Newell D, Yong C. A New Load-Transfer Factor to the Slipping Analytical Formulation in Axially Loaded Piles. Geotechnics. 2022; 2(1):171-190. https://doi.org/10.3390/geotechnics2010008
Chicago/Turabian StyleLo, Kelvin, Erwin Oh, Darren Newell, and Choo Yong. 2022. "A New Load-Transfer Factor to the Slipping Analytical Formulation in Axially Loaded Piles" Geotechnics 2, no. 1: 171-190. https://doi.org/10.3390/geotechnics2010008
APA StyleLo, K., Oh, E., Newell, D., & Yong, C. (2022). A New Load-Transfer Factor to the Slipping Analytical Formulation in Axially Loaded Piles. Geotechnics, 2(1), 171-190. https://doi.org/10.3390/geotechnics2010008







