Rock Joint Roughness Measurement and Quantification—A Review of the Current Status
Abstract
1. Introduction
2. Rock Joint Roughness Measurement Techniques
2.1. Contact Methods
2.2. Non Contact Methods
3. Rock Joint Roughness Quantification Methods
3.1. Empirical Methods
3.2. Statistical Methods
3.2.1. Amplitude-Based Roughness Parameters
3.2.2. Slope-Based Roughness Parameters
3.2.3. Amplitude and Slope-Based Roughness Parameters
3.2.4. Relations between JRC and Statistical Parameters
3.3. Fractals-Based Methods
4. Effect of Non-Stationarity on Computed Roughness Parameters
5. Effect of Heterogeneity on Computed Roughness Parameters
6. Effect of Joint Size on Computed Roughness Parameters
7. Roughness Anisotropy
8. Effect of Sampling Interval and Resolution on Computed Roughness Parameters
9. Comparison between the Values Obtained for some of the Roughness Parameters
10. Discussion and Conclusions
11. Recommendations for Future Research
Funding
Conflicts of Interest
References
- Barton, N. Review of a new shear-strength criterion for rock joints. Eng. Geol. 1973, 7, 287–332. [Google Scholar] [CrossRef]
- Bandis, S.; Lumsden, A.C.; Barton, N.R. Experimental studies of scale effects on the shear behaviour of rock joints. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1981, 18, 1–21. [Google Scholar] [CrossRef]
- Kulatilake, P.H.S.W.; Shou, G.; Huang, T.; Morgan, R. New peak shear strength criteria for anisotropic rock joints. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1995, 32, 673–697. [Google Scholar] [CrossRef]
- Barton, N.; Bandis, S.; Bakhtar, K. Strength, deformation and conductivity coupling of rock joints. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1985, 22, 121–140. [Google Scholar] [CrossRef]
- Kulatilake, P.H.S.W.; Park, J.; Balasingam, P.; Morgan, R. Quantification of aperture and relations between aperture, normal stress and fluid flow for natural single rock fractures. Geotech. Geol. Eng. 2008, 26, 269–281. [Google Scholar] [CrossRef]
- Fecker, E.; Rengers, N. Measurement of large scale roughness of rock planes by means of profilograph and geological compass. In Proceedings of the 1st ISRM Symposium on Rock Fracture, Nancy, France, 4–6 October 1971. [Google Scholar]
- Brown, S.R.; Scholz, C.H. Broad bandwidth study of the topography of natural rock surfaces. J. Geophys. Res. Solid 1985, 90, 12575–12582. [Google Scholar] [CrossRef]
- Maerz, N.H.; Franklin, J.A.; Bennett, C.P. Joint roughness measurement using shadow profilometry. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1990, 27, 329–343. [Google Scholar] [CrossRef]
- Aydan, Ö.; Shimizu, Y.; Kawamoto, T. The anisotropy of surface morphology characteristics of rock discontinuities. Rock Mech. Rock Eng. 1996, 29, 47–59. [Google Scholar] [CrossRef]
- Rasouli, V.; Harrison, J.P. A comparison of linear profiling and an in-plane method for the analysis of rock surface geometry. Int. J. Rock Mech. Min. 2004, 41, 133–138. [Google Scholar] [CrossRef]
- Develi, K.; Babadagli, T.; Comlekci, C. A new computer-controlled surface-scanning device for measurement of fracture surface roughness. Comput. Geotech. 2001, 27, 265–277. [Google Scholar] [CrossRef]
- Du, S. Research on complexity of surface undulating shapes of rock joints. J. China Univ. Geosci. 1998, 9, 86–89. [Google Scholar]
- Du, S.; Hu, Y.; Hu, X. Measurement of joint roughness coefficient by using profilograph and roughness ruler. J. Earth Sci. 2009, 20, 890–896. [Google Scholar] [CrossRef]
- Huang, S.; Oelfke, S.; Speck, R. Applicability of fractal characterization and modelling to rock joint profiles. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1992, 29, 89–191. [Google Scholar] [CrossRef]
- Hsiung, S.; Ghosh, A.; Ahola, M.; Chowdhury, A. Assessment of conventional methodologies for joint roughness coefficient determination. In Proceedings of the 34th US Symposium on Rock Mechanics (USRMS), Madison, WI, USA, 27–30 June 1993. [Google Scholar]
- Brown, S.R. Simple mathematical model of a rough fracture. J. Geophys. Res. Solid 1995, 100, 5941–5952. [Google Scholar] [CrossRef]
- Kulatilake, P.H.S.W.; Balasingam, P.; Park, J.; Morgan, R. Natural rock joint roughness quantification through fractal techniques. Geotech. Geol. Eng. 2006, 24, 1181–1202. [Google Scholar] [CrossRef]
- Xie, H.; Wang, J.-A.; Xie, W.-H. Fractal effects of surface roughness on the mechanical behavior of rock joints. Chaos Soliton Fract. 1997, 8, 221–252. [Google Scholar] [CrossRef]
- Lanaro, F.; Jing, L.; Stephansson, O. 3-D-laser measurements and representation of roughness of rock fractures. In Mechanics of Jointed and Faulted Rock; Routledge: Oxford, UK, 1998; pp. 185–189. [Google Scholar]
- Belem, T.; Homand-Etienne, F.; Souley, M. Quantitative parameters for rock joint surface roughness. Rock Mech. Rock Eng. 2000, 33, 217–242. [Google Scholar] [CrossRef]
- Grasselli, G.; Wirth, J.; Egger, P. Quantitative three-dimensional description of a rough surface and parameter evolution with shearing. Int. J. Rock Mech. Min. 2002, 39, 789–800. [Google Scholar] [CrossRef]
- Feng, Q.; Fardin, N.; Jing, L.; Stephansson, O. A new method for in-situ non-contact roughness measurement of large rock fracture surfaces. Rock Mech. Rock Eng. 2003, 36, 3–25. [Google Scholar] [CrossRef]
- Fardin, N.; Feng, Q.; Stephansson, O. Application of a new in situ 3D laser scanner to study the scale effect on the rock joint surface roughness. Int. J. Rock Mech. Min. 2004, 41, 329–335. [Google Scholar] [CrossRef]
- Ge, Y.; Kulatilake, P.H.S.W.; Tang, H.; Xiong, C. Investigation of natural rock joint roughness. Comput. Geotech. 2014, 55, 290–305. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, B.; Tanabashi, Y. Estimating the relation between surface roughness and mechanical properties of rock joints. Int. J. Rock Mech. Min. 2006, 43, 837–846. [Google Scholar] [CrossRef]
- Tatone, B.S.; Grasselli, G. A method to evaluate the three-dimensional roughness of fracture surfaces in brittle geomaterials. Rev. Sci. Instrum. 2009, 80, 125110. [Google Scholar] [CrossRef] [PubMed]
- Hong, E.S.; Lee, J.S.; Lee, I.M. Underestimation of roughness in rough rock joints. Int. J. Numer. Anal. Methods Geomech. 2008, 32, 1385–1403. [Google Scholar] [CrossRef]
- Yong, R.; Ye, J.; Li, B.; Du, S.-G. Determining the maximum sampling interval in rock joint roughness measurements using Fourier series. Int. J. Rock Mech. Min. 2018, 101, 78–88. [Google Scholar] [CrossRef]
- Myers, N.O. Characterization of surface roughness. Wear 1962, 5, 182–189. [Google Scholar] [CrossRef]
- Mandelbrot, B. How long is the coast of Britain? Statistical self-similarity and fractional dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef]
- Sayles, R.S.; Thomas, T.R. The spatial representation of surface roughness by means of the structure function: A practical alternative to correlation. Wear 1977, 42, 263–276. [Google Scholar] [CrossRef]
- Wu, T.H.; Ali, E.M. Statistical representation of the joint roughness. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1978, 259–262. [Google Scholar] [CrossRef]
- Tse, R.; Cruden, D. Estimating joint roughness coefficients. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1979, 16, 303–307. [Google Scholar] [CrossRef]
- Yu, X.; Vayssade, B. Joint profiles and their roughness parameters. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1991, 28, 333–336. [Google Scholar] [CrossRef]
- Tatone, B.S.A.; Grasselli, G. A new 2D discontinuity roughness parameter and its correlation with JRC. Int. J. Rock Mech. Min. 2010, 47, 1391–1400. [Google Scholar] [CrossRef]
- Tatone, B.S.; Grasselli, G. An investigation of discontinuity roughness scale dependency using high-resolution surface measurements. Rock Mech. Rock Eng. 2013, 46, 657–681. [Google Scholar] [CrossRef]
- Feder, J. Fractals; Plenum Press: New York, NY, USA, 1988. [Google Scholar]
- Russ, J.C. Fractal Surfaces; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Shirono, T.; Kulatilake, P.H.S.W. Accuracy of the spectral method in estimating fractal/spectral parameters for self-affine roughness profiles. Int. J. Rock Mech. Min. 1997, 34, 789–804. [Google Scholar] [CrossRef]
- Roko, R.O.; Daemen, J.J.K.; Myers, D.E. Variogram characterization of joint surface morphology and asperity deformation during shearing. Int. J. Rock Mech. Min. 1997, 34, 71–84. [Google Scholar] [CrossRef]
- Kulatilake, P.H.S.W.; Um, J.; Pan, G. Requirements for accurate quantification of self-affine roughness using the variogram method. Int. J. Solids Struct. 1998, 35, 4167–4189. [Google Scholar] [CrossRef]
- Kulatilake, P.H.S.W.; Um, J. Requirements for accurate quantification of self-affine roughness using the roughness–length method. Int. J. Rock Mech. Min. 1999, 36, 5–18. [Google Scholar] [CrossRef]
- Ankah, M.L.Y.; Kulatilake, P.H.; Sunkpal, D.T.; Zhao, X. Rock Joint Roughness Quantification Using 2D And 3D Fractal Methods. Fractals 2022, 30, 1–16. [Google Scholar] [CrossRef]
- Lanaro, F. A random field model for surface roughness and aperture of rock fractures. Int. J. Rock Mech. Min. 2000, 37, 1195–1210. [Google Scholar] [CrossRef]
- Barton, N.; Choubey, V. The shear strength of rock joints in theory and practice. Rock Mech. 1977, 10, 1–54. [Google Scholar] [CrossRef]
- Miller, S.; McWilliams, P.; Kerkering, J. Ambiguities in estimating fractal dimensions of rock fracture surfaces. In Proceedings of the 31st US Symposium on Rock Mechanics (USRMS), Golden, CO, USA, 18–20 June 1990. [Google Scholar]
- Kodikara, J.K.; Johnston, I.W. Shear behaviour of irregular triangular rock-concrete joints. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1994, 31, 313–322. [Google Scholar] [CrossRef]
- Alameda-Hernández, P.; Jiménez-Perálvarez, J.; Palenzuela, J.A.; El Hamdouni, R.; Irigaray, C.; Cabrerizo, M.A.; Chacón, J. Improvement of the JRC calculation using different parameters obtained through a new survey method applied to rock discontinuities. Rock Mech. Rock Eng. 2014, 47, 2047–2060. [Google Scholar] [CrossRef]
- Milne, D.; Germain, P.; Potvin, Y. Measurement of rock mass properties for mine design. In Proceedings of the Rock Characterization: ISRM Symposium, Eurock’92, Chester, UK, 14–17 September 1992. [Google Scholar]
- Rasouli, V.; Harrison, J.P. Scale effect, anisotropy and directionality of discontinuity surface roughness. In Proceedings of the EUROCK Symposium, Aachen, Germany, 27 March 2000; Volume 14, pp. 751–756. [Google Scholar]
- Yong, R.; Ye, J.; Liang, Q.-F.; Huang, M.; Du, S.-G. Estimation of the joint roughness coefficient (JRC) of rock joints by vector similarity measures. Bull. Eng. Geol. Environ. 2018, 77, 735–749. [Google Scholar] [CrossRef]
- Tatone, B.S.A.; Grasselli, G. Use of a Stereo-Topometric Measurement System for the Characterization of Rock Joint Roughness In-Situ and in the Laboratory. Available online: extension://bfdogplmndidlpjfhoijckpakkdjkkil/pdf/viewer.html?file=https%3A%2F%2Fgeogroup.utoronto.ca%2Fwp-content%2Fuploads%2FRockEng09%2FPDF%2FSession15%2F4145%2520PAPER.pdf (accessed on 20 February 2023).
- Lee, H.-S.; Ahn, K.-W. A prototype of digital photogrammetric algorithm for estimating roughness of rock surface. Geosci. J. 2004, 8, 333–341. [Google Scholar] [CrossRef]
- Baker, B.R.; Gessner, K.; Holden, E.-J.; Squelch, A.P. Automatic detection of anisotropic features on rock surfaces. Geosphere 2008, 4, 418–428. [Google Scholar] [CrossRef]
- Barton, N. Barton-Bandis Criterion Summarized with Figures. 2017. Available online: http://www.nickbarton.com/downloads_04.asp (accessed on 5 February 2023).
- ISRM. Suggested Methods for the Quantitative Description of Discontinuities in Rock Masses. In Rock Characterization, Testing and Monitoring—ISRM Suggested Methods; Brown, E.T., Ed.; Pergamon Press: Oxford, UK, 1981; pp. 3–52. [Google Scholar]
- Ünlüsoy, D.; Süzen, M.L. A new method for automated estimation of joint roughness coefficient for 2D surface profiles using power spectral density. Int. J. Rock Mech. Min. Sci. 2020, 125, 104156. [Google Scholar] [CrossRef]
- Grasselli, G.; Egger, P. Constitutive law for the shear strength of rock joints based on three-dimensional surface parameters. Int. J. Rock Mech. Min. Sci. 2003, 40, 25–40. [Google Scholar] [CrossRef]
- Beer, A.J.; Stead, D.; Coggan, J.S. Technical note estimation of the joint roughness coefficient (JRC) by visual comparison. Rock Mech. Rock Eng. 2002, 35, 65–74. [Google Scholar] [CrossRef]
- Wu, X.; Zheng, H.; Jiang, Y. Influence of joint roughness on the shear properties of energy-absorbing bolt. Int. J. Rock Mech. Min. 2023, 163, 105322. [Google Scholar] [CrossRef]
- Jang, H.-S.; Kang, S.-S.; Jang, B.-A. Determination of joint roughness coefficients using roughness parameters. Rock Mech. Rock Eng. 2014, 47, 2061–2073. [Google Scholar] [CrossRef]
- El-Soudani, S.M. Profilometric analysis of fractures. Metallography 1978, 11, 247–336. [Google Scholar] [CrossRef]
- Zhang, G.; Karakus, M.; Tang, H.; Ge, Y.; Zhang, L. A new method estimating the 2D joint roughness coefficient for discontinuity surfaces in rock masses. Int. J. Rock Mech. Min. Sci. 2014, 72, 191–198. [Google Scholar] [CrossRef]
- Mo, P.; Li, Y. Estimating the three-dimensional joint roughness coefficient value of rock fractures. Bull. Eng. Geol. Environ. 2019, 78, 857–866. [Google Scholar] [CrossRef]
- Ankah, M.L.Y.; Sunkpal, D.T.; Zhao, X.; Kulatilake, P.H.S.W. Role of heterogeneity on joint size effect, and influence of anisotropy and sampling interval on rock joint roughness quantification. Geomech. Geophys 2022, 8, 101. [Google Scholar] [CrossRef]
- McGough, M.; Kimes, L.; Harris, A.; Kreidl, O.P.; Hudyma, N. Investigation of roughness algorithms applied to jrc profiles for assessment of weathering. In Proceedings of the 49th US Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 29 June–1 July 2015. [Google Scholar]
- Belem, T.; Souley, M.; Homand, F. Modeling surface roughness degradation of rock joint wall during monotonic and cyclic shearing. Acta Geotech. 2007, 2, 227–248. [Google Scholar] [CrossRef]
- Liu, Q.; Tian, Y.; Liu, D.; Jiang, Y. Updates to JRC-JCS model for estimating the peak shear strength of rock joints based on quantified surface description. Eng. Geol. 2017, 228, 282–300. [Google Scholar] [CrossRef]
- Grasselli, G. Shear Strength of Rock Joints Based on Quantified Surface Description. Ph.D. Thesis, Ecole Polytechnique Federale de Lausanne, Lausanne, Switzerland, 2001. [Google Scholar]
- Li, Y.; Zhang, Y. Quantitative estimation of joint roughness coefficient using statistical parameters. Int. J. Rock Mech. Min. 2015, 100, 27–35. [Google Scholar] [CrossRef]
- Yang, Z.; Di, C.; Yen, K. The effect of asperity order on the roughness of rock joints. Int. J. Rock Mech. Min. 2001, 38, 745–752. [Google Scholar] [CrossRef]
- Gravanis, E.; Pantelidis, L. Determining of the Joint Roughness Coefficient (JRC) of Rock Discontinuities Based on the Theory of Random Fields. Geosci. J. 2019, 9, 295. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Self-affine fractals and fractal dimension. Phys. Scr. 1985, 32, 257. [Google Scholar] [CrossRef]
- Orey, S. Gaussian sample functions and the Hausdorff dimension of level crossings. Z. Für Wahrscheinlichkeitstheorie Und Verwandte Geb. 1970, 15, 249–256. [Google Scholar] [CrossRef]
- Berry, M.V.; Lewis, Z.; Nye, J.F. On the Weierstrass-Mandelbrot fractal function. Proc. R. Soc. Lond. A Math. Phys. Sci. 1980, 370, 459–484. [Google Scholar]
- Malinverno, A. A simple method to estimate the fractal dimension of a self-affine series. Geophys. Res. Lett. 1990, 17, 1953–1956. [Google Scholar] [CrossRef]
- Power, W.L.; Tullis, T.E. Euclidean and fractal models for the description of rock surface roughness. J. Geophys. Res. Solid 1991, 96, 415–424. [Google Scholar] [CrossRef]
- Poon, C.; Sayles, R.; Jones, T. Surface measurement and fractal characterization of naturally fractured rocks. J. Phys. D 1992, 25, 1269. [Google Scholar] [CrossRef]
- Fardin, N.; Stephansson, O.; Jing, L. The scale dependence of rock joint surface roughness. Int. J. Rock Mech. Min. 2001, 38, 659–669. [Google Scholar] [CrossRef]
- Kulatilake, P.H.S.W.; Du, S.-G.; Ankah, M.L.Y.; Yong, R.; Sunkpal, D.T.; Zhao, X.; Liu, G.-J.; Wu, R. Non-stationarity, heterogeneity, scale effects, and anisotropy investigations on natural rock joint roughness using the variogram method. Bull. Eng. Geol. Environ. 2021, 80, 6121–6143. [Google Scholar] [CrossRef]
- Kulatilake, P.H.S.W.; Um, J.; Panda, B.B.; Nghiem, N. Development of new peak shear-strength criterion for anisotropic rock joints. J. Eng. Mech. 1999, 125, 1010–1017. [Google Scholar] [CrossRef]
- Fardin, N. Influence of structural non-stationarity of surface roughness on morphological characterization and mechanical deformation of rock joints. Rock Mech. Rock Eng. 2008, 41, 267–297. [Google Scholar] [CrossRef]
- Jiang, Q.; Feng, X.; Gong, Y.; Song, L.; Ran, S.; Cui, J. Reverse modelling of natural rock joints using 3D scanning and 3D printing. Comput. Geotech. 2016, 73, 210–220. [Google Scholar] [CrossRef]
- Ge, Y.; Lin, Z.; Tang, H.; Zhao, B.; Chen, H.; Xie, Z.; Du, B. Investigation of the effects of nonstationary features on rock joint roughness using the laser scanning technique. Bull. Eng. Geol. Environ. 2020, 79, 3163–3174. [Google Scholar] [CrossRef]
- Swan, G.; Zongqi, S. Prediction of shear behaviour of joints using profiles. Rock Mech. Rock Eng. 1985, 18, 183–212. [Google Scholar] [CrossRef]
- Cravero, M.; Iabichino, G.; Ferrero, A.M. Evaluation of joint roughness and dilatancy of schistosity joints. In Rock mechanics-a challenge for society. In Proceedings of the ISRM Regional Symposium EUROCK 2001, Espoo, Finland, 4–7 June 2001; pp. 217–222. [Google Scholar]
- Cravero, M.; Iabichino, G.; Piovano, V. Analysis of large joint profiles related to rock slope instabilities. In Proceedings of the 8th ISRM Congress, Tokyo, Japan, 25–29 September 1995. [Google Scholar]
- Lanaro, F.; Jing, L.; Stephansson, O. Scale dependency of roughness and stationarity of rock joints. In Proceedings of the 9th ISRM Congress, Paris, France, 25–28 August 1999. [Google Scholar]
- Leal-Gomes, M.J.A. Some new essential questions about scale effects on the mechanics of rock mass joints. In Proceedings of the 10th ISRM Congress, Sandton, South Africa, 8–12 September 2003; The South African Institute of Mining & Metallurgy: Johannesburg, South Africa, 2003. [Google Scholar]
- Ge, Y.; Tang, H.; Eldin, M.M.E.; Chen, P.; Wang, L.; Wang, J. A description for rock joint roughness based on terrestrial laser scanner and image analysis. Sci. Rep. 2015, 5, 16999. [Google Scholar] [CrossRef]
- Chen, S.J.; Zhu, W.C.; Yu, Q.L.; Liu, X.G. Characterization of Anisotropy of Joint Surface Roughness and Aperture by Variogram Approach Based on Digital Image Processing Technique. Rock Mech. Rock Eng. 2016, 49, 855–876. [Google Scholar] [CrossRef]
- Bao, H.; Xu, X.; Lan, H.; Zhang, G.; Yin, P.; Yan, C.; Xu, J. A new joint morphology parameter considering the effects of micro-slope distribution of joint surface. Eng. Geol. 2020, 275, 105734. [Google Scholar] [CrossRef]
- Chen, X.; Zeng, Y.; Ye, Y.; Sun, H.; Tang, Z.; Zhang, X. A Simplified form of Grasselli’s 3D Roughness Measure θmax*/(C + 1). Rock Mech. Rock Eng. 2021, 54, 4329–4346. [Google Scholar] [CrossRef]
- Tang, Z.C.; Jiao, Y.Y.; Wong, L.N.Y.; Wang, X.C. Choosing appropriate parameters for developing empirical shear strength criterion of rock joint: Review and new insights. Rock Mech. Rock Eng. 2016, 49, 4479–4490. [Google Scholar] [CrossRef]
- Pickering, C.; Aydin, A. Modeling roughness of rock discontinuity surfaces: A signal analysis approach. Rock Mech. Rock Eng. 2016, 49, 2959–2965. [Google Scholar] [CrossRef]
- Li, Y.; Xu, Q.; Aydin, A. Uncertainties in estimating the roughness coefficient of rock fracture surfaces. Bull. Eng. Geol. Environ. 2017, 76, 1153–1165. [Google Scholar] [CrossRef]

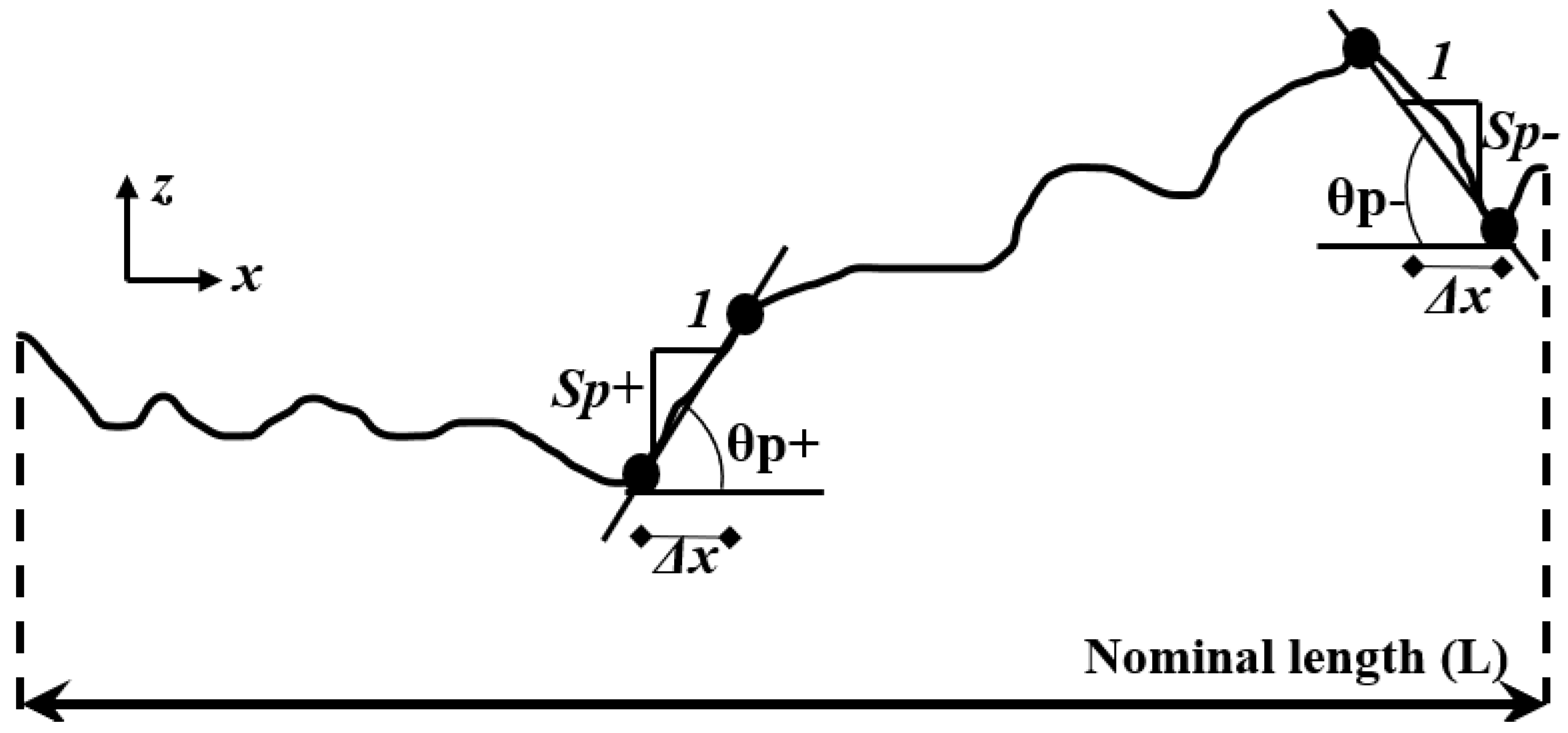




| Roughness Metric Number | Roughness Metric | Abbreviation | Reference(s) |
|---|---|---|---|
| 1 | Centerline average value of the profile | CLA | Tse and Cruden [33] |
| 2 | The mean square value of the profile | MSV | Tse and Cruden [33] |
| 3 | Root mean square value of the profile, | RMS | Myers [29]; Tse and Cruden [33] |
| 4 | The mean inclination angle of the profile | θP | Yu and Vayssade [34]; Belem et al. [20] |
| 5 | The mean positive inclination angle of the profile | θP+ | Belem et al. [20] |
| 6 | The mean negative inclination angle of the profile | θP− | Belem et al. [20] |
| 7 | The standard deviation of the inclination angle of the profile | SD θP | Yu and Vayssade [34] |
| 8 | Root mean square of the slope of the profile | Z2 | Myers [29]; Tse and Cruden [33]; Yu and Vayssade [34] |
| 9 | Root mean square of the first derivative of the slope of the profile | Z3 | Myers [29]; Tse and Cruden [33] |
| 10 | Percentage excess distance measured along the profile where the slope is positive over the distance where the slope is negative | Z4 | Myers [29]; Tse and Cruden [33] |
| 11 | Autocorrelation function | ACF | Myers [29]; Wu and Ali [32] |
| 12 | Structure-function | SF | Myers [29]; Sayles and Thomas [31]; Yu and Vayssade [34] |
| 13 | Spectral density function | SDF | Wu and Ali [32] |
| 14 | Mean inclination angle for the surface | θS | Belem et al. [20] |
| 15 | Root mean square of the slope of the surface | Z2S | Belem et al. [20] |
| 16 | Maximum apparent dip angle in the shear direction/an empirical roughness parameter +1 | θMax/C + 1 | Grasselli et al. [21]; Tatone and Grasselli [36] |
| 17 | Roughness profile index | RP | Mandelbrot [30], Maerz et al. [8]; Yu and Vayssade [34] |
| 18 | Surface roughness coefficient | RS | El-Soudani [62];Belem et al. [20] |
| 19 | Surface Tortuosity coefficient | TS | Belem et al. [20] |
| No. | Parameter | Formula | Equation No. | Reference(s) |
|---|---|---|---|---|
| 1 | (1) | Tse and Cruden [33] | ||
| 2 | (2) | Myers [29]; Tse and Cruden [33]; | ||
| 3 | (3) | Tse and Cruden [33] | ||
| 4 | (4) | Belem et al. [20] | ||
| 5 | (5) | Belem et al. [20] | ||
| 6 | (6) | Belem et al. [20] | ||
| 7 | (7) | Belem et al. [20] | ||
| 8 | (8) | Myers [29]; Tse and Cruden [33]; Yu and Vayssade [34] | ||
| 9 | (9) | Myers [29]; Sayles and Thomas [31]; Yu and Vayssade [34] | ||
| 10 | (10) | Myers [29]; Tse and Cruden [33] | ||
| 11 | (11) | Myers [29]; Tse and Cruden [33] | ||
| 12 | (12) | Yu and Vayssade [34] | ||
| 13 | (13) | Mandelbrot [30] | ||
| 14 | (14) | Belem et al. [20] | ||
| 15 | (15a) | Belem et al. [20] | ||
| (15b) | ||||
| 16 | (16) | Tatone and Grasselli [26] |
| No. | Equation | R | Reference |
|---|---|---|---|
| 1 | 0.993 | Yang et al. [71] | |
| 2 | 0.973 | Yu and Vayssade [34] | |
| 3 | 0.975 | Yu and Vayssade [34] | |
| 4 | 0.934 | Yu and Vayssade [34] | |
| 5 | 0.973 | Yu and Vayssade [34] | |
| 6 | 0.954 | Yu and Vayssade [34] | |
| 7 | ---- | Tatone and Grasselli [35] | |
| 8 | 0.884 | Li and Zhang [70] | |
| 9 | 0.876 | Li and Zhang [70] | |
| 10 | 0.993 | Yu and Vayssade [34] | |
| 11 | 0.972 | Yu and Vayssade [34] | |
| 12 | 0.954 | Yu and Vayssade [34] | |
| 13 | ------ | Tatone and Grasselli [35] | |
| 14 | 0.945 | Yu and Vayssade [34] | |
| 15 | 0.974 | Yu and Vayssade [34] | |
| 16 | 0.975 | Yu and Vayssade [34] | |
| 17 | 0.970 | Yu and Vayssade [34] | |
| 18 | 0.971 | Tatone and Grasselli [35] | |
| 19 | 0.900 | Gravanis and Pantelidis [72] |
| Case | No. of Data | Rp | θP | θP− | |||
|---|---|---|---|---|---|---|---|
| Mean | CV * | Mean | CV * | Mean | CV * | ||
| 125 mm Z-Y profiles (0–125 mm) | 101 | 1.0166 | 0.0046 | 7.8842 | 0.1240 | −8.7253 | 0.1466 |
| 125 mm Z-Y profiles (125–250 mm) | 101 | 1.0186 | 0.0058 | 8.2994 | 0.1238 | −8.9835 | 0.1511 |
| 125 mm Z-Y profiles (250–375 mm) | 101 | 1.0195 | 0.0067 | 8.6479 | 0.1630 | −9.3509 | 0.1576 |
| 125 mm Z-Y profiles (375–500 mm) | 101 | 1.0177 | 0.0059 | 8.2288 | 0.1528 | −8.7103 | 0.1902 |
| 125 mm Z-Y profiles (500–625 mm) | 101 | 1.0191 | 0.0049 | 8.4616 | 0.1039 | −7.2657 | 0.1783 |
| 125 mm Z-Y profiles (625–750 mm) | 101 | 1.0179 | 0.0049 | 8.4051 | 0.1401 | −8.5723 | 0.1574 |
| 125 mm Z-Y profiles (750–875 mm) | 101 | 1.0529 | 0.0260 | 10.7150 | 0.1734 | −10.4767 | 0.1933 |
| 125 mm Z-Y profiles (875–1000 mm) | 101 | 1.0416 | 0.0157 | 10.6827 | 0.1431 | −10.8429 | 0.1764 |
| Case | No. of Data | Rp | θp | θP− | |||
|---|---|---|---|---|---|---|---|
| Mean | CV * | Mean | CV * | Mean | CV * | ||
| 125 mm Z-X profiles (0–125 mm) | 51 | 1.0056 | 0.0041 | 4.0701 | 0.2572 | −4.1471 | 0.3755 |
| 125 mm Z-X profiles (125–250 mm) | 51 | 1.0059 | 0.0029 | 4.3144 | 0.2328 | −4.5201 | 0.2972 |
| 125 mm Z-X profiles (250–375 mm) | 51 | 1.0044 | 0.0021 | 3.8270 | 0.2222 | −3.9846 | 0.2871 |
| 125 mm Z-X profiles (375–500 mm) | 51 | 1.0060 | 0.0081 | 3.8499 | 0.3014 | −3.3280 | 0.3162 |
| 125 mm Z-X profiles (500–625 mm) | 51 | 1.0046 | 0.0025 | 3.9029 | 0.2484 | −3.6263 | 0.2583 |
| 125 mm Z-X profiles (625–750 mm) | 51 | 1.0045 | 0.0029 | 3.7001 | 0.2966 | −3.2946 | 0.3377 |
| 125 mm Z-X profiles (750–875 mm) | 51 | 1.0042 | 0.0025 | 3.6848 | 0.2718 | −3.3629 | 0.3017 |
| 125 mm Z-X profiles (875–1000 mm) | 51 | 1.0036 | 0.0022 | 3.3642 | 0.2694 | −3.0815 | 0.3524 |
| Case | No. of Data | Dv | Kv | Dv × Kv | |
|---|---|---|---|---|---|
| Mean | Mean | Mean | |||
| 250 mm Z-X profiles | 0–250 mm | 51 | 1.1220 | 0.0108 | 0.0121 |
| 250–500 mm | 51 | 1.1598 | 0.0092 | 0.0107 | |
| 500–750 mm | 51 | 1.1249 | 0.0085 | 0.0096 | |
| 750–1000 mm | 51 | 1.1515 | 0.0071 | 0.0082 | |
| 250 mm Z-Y profiles | 0–250 mm | 101 | 1.1287 | 0.0352 | 0.0397 |
| 250–500 mm | 101 | 1.1183 | 0.0368 | 0.0412 | |
| 500–750 mm | 101 | 1.1284 | 0.0370 | 0.0418 | |
| 750–1000 mm | 78 | 1.3780 | 0.0812 | 0.1119 | |
| Case | No. of Data | DRL | A | DRL × A | |
|---|---|---|---|---|---|
| Mean | Mean | Mean | |||
| 250 mm Z-X profiles | 0–250 mm | 101 | 1.0720 | 0.0088 | 0.0094 |
| 250–500 mm | 101 | 1.1213 | 0.0089 | 0.0100 | |
| 500–750 mm | 101 | 1.0807 | 0.0081 | 0.0088 | |
| 750–1000 mm | 101 | 1.1299 | 0.0082 | 0.0093 | |
| 250 mm Z-Y profiles | 0–250 mm | 101 | 1.0881 | 0.0188 | 0.0205 |
| 250–500 mm | 101 | 1.0746 | 0.0189 | 0.0203 | |
| 500–750 mm | 101 | 1.1234 | 0.0215 | 0.0242 | |
| 750–1000 mm | 101 | 1.1851 | 0.0318 | 0.0377 | |
| Case | No. of Data | Rp | θP | θP− | |||
|---|---|---|---|---|---|---|---|
| Mean | CV * | Mean | CV * | Mean | CV * | ||
| 500 mm Z-Y profiles (0–500 mm) | 101 | 1.0181 | 0.0032 | 8.2674 | 0.0919 | −8.9498 | 0.0921 |
| 250 mm Z-Y profiles (0–500 mm) lumped | 202 | 1.0181 | 0.0045 | 8.2666 | 0.1145 | −8.9367 | 0.1267 |
| 125 mm Z-Y profiles (0–500 mm) lumped | 404 | 1.0181 | 0.0059 | 8.2650 | 0.1466 | −8.9425 | 0.1646 |
| Case | No. of Data | Rp | θP | θP− | |||
|---|---|---|---|---|---|---|---|
| Mean | CV * | Mean | CV * | Mean | CV * | ||
| 1000 mm Z-X profiles | 101 | 1.0049 | 0.0016 | 3.8429 | 0.1061 | −3.8056 | 0.1164 |
| 1000 mm Z-Y profiles | 101 | 1.0255 | 0.0043 | 8.9285 | 0.0652 | −9.1881 | 0.0604 |
| 500 mm Z-X profiles | 402 | 1.0048 | 0.0022 | 3.8386 | 0.1582 | −3.7534 | 0.1968 |
| 500 mm Z-Y profiles | 202 | 1.0255 | 0.0092 | 8.9211 | 0.1105 | −9.2025 | 0.0920 |
| 250 mm Z-X profiles | 804 | 1.0048 | 0.0029 | 3.8393 | 0.2117 | −3.7265 | 0.2632 |
| 250 mm Z-Y profiles | 404 | 1.0255 | 0.0144 | 8.9181 | 0.1570 | −9.1591 | 0.1596 |
| 125 mm Z-X profiles | 408 | 1.0048 | 0.0040 | 3.8392 | 0.2716 | −3.6682 | 0.3438 |
| 125 mm Z-Y profiles | 808 | 1.0255 | 0.0174 | 8.9156 | 0.1874 | −9.1160 | 0.2074 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kulatilake, P.H.S.W.; Ankah, M.L.Y. Rock Joint Roughness Measurement and Quantification—A Review of the Current Status. Geotechnics 2023, 3, 116-141. https://doi.org/10.3390/geotechnics3020008
Kulatilake PHSW, Ankah MLY. Rock Joint Roughness Measurement and Quantification—A Review of the Current Status. Geotechnics. 2023; 3(2):116-141. https://doi.org/10.3390/geotechnics3020008
Chicago/Turabian StyleKulatilake, Pinnaduwa H. S. W., and Mawuko Luke Yaw Ankah. 2023. "Rock Joint Roughness Measurement and Quantification—A Review of the Current Status" Geotechnics 3, no. 2: 116-141. https://doi.org/10.3390/geotechnics3020008
APA StyleKulatilake, P. H. S. W., & Ankah, M. L. Y. (2023). Rock Joint Roughness Measurement and Quantification—A Review of the Current Status. Geotechnics, 3(2), 116-141. https://doi.org/10.3390/geotechnics3020008







