Non-Linear Numerical Modelling of Sustainable Advanced Composite Columns Made from Bamboo Culms

Abstract

The present article uses the finite element analysis (FEA) software ABAQUS to model a bamboo-based advanced composite column for construction. Different numerical models were analysed to be able to predict the behaviour of a bamboo-based composite column tested by the same group. Bamboo-based composites maintain the inherent excellent mechanical properties of raw bamboo whilst adding a certain degree of processing and engineering. Thus, the composite individual samples are more consistent and reliable when compared with their raw counterparts. A buckling analysis is carried out to determine the response of the composites to axial compressive loading. Different modelling elements and imperfection parameters were implemented separately in different FEA models so that the efficacy of each could be established and suggestions could be made with regard to the modelling elements and size of imperfection that should be used in future models. The results are compared to empirical findings, giving insights into the quality of results that can be obtained using numerical modelling. This also allowed for an evaluation of the methods and assumptions applied in the model. The load at rupture and displacements obtained by the numerical model were comparable to the experimental findings, with only minor differences observed.

1. Introduction

In recent times there have been increased efforts to develop more sustainable and environmentally friendly practices in the construction industry. The built environment contributes significantly to carbon dioxide emissions, destruction of the natural environment, and consumption of resources, with the materials used in the construction industry being partly to blame. Currently, the built environment has a direct impact on the earth and uses 12.2% of the planet’s consumed water, 40% of the earth’s total materials, 40% of the total energy, and 55% of the planet’s woodcut, excluding the wood used as fuel [1]. Additional research by Hoffman and Henn [2] states that in the United States, 71% of electricity and 40% of non-industrial waste is a result of the built environment. In addition, they state that 36% of the carbon dioxide emissions that cause global warming are a consequence of the built environment. Furthermore, the construction industry gives rise to indirect impacts such as deforestation and soil erosion, biodiversity loss across the earth as a whole, eutrophication and acidification of the planet’s water sources, and the generation and release of toxic substances and endocrine disruptors that are detrimental to health [1]. The issue of making the sector more sustainable and less environmentally harmful is multifaceted; technological, economic, and psychological, with social barriers that all play a role in how much progression is made [2].

Bamboo is a cost-effective and sustainable material that grows rapidly in many parts of the world; it has a small embodied energy, the ability to take in and store carbon from the environment during its growth, and excellent mechanical properties [3]. However, bamboo is a natural material and has inherent variation between specimens, thus being hard to standardise. The present paper focuses on materials that are less established in the construction industry such as bamboo-based engineered materials. These materials need to possess properties that equal or surpass conventional materials whilst being less environmentally damaging.

1.1. Why Bamboo?

Bamboo is a giant grass that grows in groups on the ground [4]. A common feature of bamboo is that it has rapid growth. Bamboo has been measured as growing as fast as 250 mm per day [5]. Consequently, it grows to full strength in as short as three to five years, allowing it to be rapidly harvested, especially when compared to other materials such as standard timber [3].

Environmental Benefits and Sustainability of Bamboo

The way in which bamboo naturally grows and is harvested means it has a number of advantages in terms of sustainability. Bamboo can grow in places such as steep slopes where timber would not be able to grow. Bamboo-based products have less eco-costs than tropical hardwood. Bamboo gives a very high yield compared to timber, especially in the production of biofuel. In addition, bamboo can be used as an alternative to tropical hardwoods reducing the burden placed on forests in tropical regions [6]. Due to the rapidity of bamboo growth, it can be harvested much more frequently than timber. On equal-sized plots of land, timber may only be able to be harvested every decade whereas bamboo can be harvested yearly. Since only mature culms are cut, when harvested no damage is made to the root system, so future growth can take place [7]. Additionally, bamboo takes in carbon whilst growing and stores this carbon when it is harvested. The sequestrated carbon will be contained and not released into the atmosphere for the duration of the bamboo product’s lifetime, knowing that bamboo can last 30–40 years in the elements when treated properly [8]. Conventional construction materials such as steel and concrete have high embodied energies due to the processes used in their manufacture. When compared to concrete, steel, and wood, bamboo has the smallest energy required for production [8]. It is clear that extensive worldwide usage of bamboo in construction will have positive effects on global sustainability.

1.2. Aim and Objectives

In the present paper, a promising bamboo-based advanced composite column proposed by Mofidi et al. [3] (Figure 1) is modelled numerically and comprehensively analysed by means of FEA. This study provides a blueprint for future attempts to model the behaviour of complex advanced composite construction materials with more than two constituents. Mofidi et al. [3] most promising sample, which offers a 294.4% increase in compressive strength when compared to raw bamboo bundle, is chosen to be modelled in ABAQUS [9]. The sample is made from full culm Moso bamboo fibres with an epoxy matrix and PVC confinement. Regardless of the synthetic base of epoxy and PVC components of the specimen, the specimen was chosen due to the widely recognised behaviour of the epoxy and PVC to be used in their corresponding constitutive models in ABAQUS. In fact, the focus of the study is on the methodology of numerical modelling for such complicated unprecedented construction materials. In future, the epoxy and PVC components will be replaced with bio-based resin matrices such as bio-epoxy and furan resins, and PVC confinement will be substituted with giant bamboo.

In particular, the aim of this article is to create a model in the FEA software ABAQUS that accurately describes the buckling behaviour of bamboo-based columns for construction. In this regard, the following objectives are considered in this study:

• Formulate constitutive models that describe the behaviours of the constituent parts of the composite bamboo columns, to be given as input to ABAQUS.
• Create numerical models that realistically represent the physical specimen produced, tested, and reported by Mofidi et al. [3].
• Use FEA to carry out a buckling analysis on the specimens under axial compressive loads considering the FEA method of analysis, Element types, and Imperfections as the parameters of the study.
• Extract the outputs from the FEA to determine the load-displacement behaviour, load at rupture, and stress distribution, and compare the results gained from the FEA with the experimental results in literature.

2. Literature Review

2.1. Research on Bamboo as a Construction Material

2.1.1. Research on Bamboo for Surface Applications

One of the main problems halting the widespread use of bamboo in the construction industry is the natural variation in raw culms and the anisotropic nature of bamboo, which contributes to standardisation difficulties. To overcome these shortcomings, bamboo-based composites can be manufactured. Sharma et al. [10] carry out testing on bamboo scrimber and laminated bamboo with results showing that both have very similar properties in tension, compression, and shear parallel to the grain, with laminated bamboo outperforming bamboo scrimber in post-peak load deformation capacity. When evaluating the properties perpendicular to the grain, the two engineered bamboo products are very similar. However, in compression, bamboo scrimber is twice as strong. Bamboo scrimber has superior strength parameters in all areas, with the exception of shear parallel to the grain. Both engineered bamboo products outperform the other materials—timber and raw bamboo—in all mechanical properties parallel to the grain with the exception of tension. Sharma et al. [10] confirm that analogous to timber, bamboo products have reduced strength perpendicular to the grain. It is also shown that laminated bamboo has a respectable flexural strength to density ratio. The bamboo products show flexural strengths that are high in the natural composite envelope and are outperformed only by highly regarded materials, such as fibre reinforced polymer composites.

Sharma et al. [11] evaluated engineered bamboo to gauge the mechanical properties of laminated composites under differing processing methods. The two processing methods they use are bleaching and caramelisation. Previous literature into the effect of processing on bamboo was limited and mostly considered raw full culm bamboo for use in a non-structural setting. Sharma et al. [11] test the specimens in compression, tension, shear, and flexion. Specimens include raw bamboo, bleached bamboo, semi-caramelised bamboo, caramelised bamboo, Sitka spruce, and Douglas fir. Although compressive and shear strength improves, the specimens become weaker in tension as the degree of processing and treatment increases. The bending modulus is also significantly increased with further processing and treatment. Sharma et al. [11] show that the flexural properties of the bamboo specimens either equal or surpass the timber specimens. However, bamboo can experience deflections that are considerably large for use in structures. In addition, they reveal that thermal treatments increase bending stiffness with the caramelised specimen having the most significant increase. The results indicate that thermal treatment reduces the modulus of rupture and at low temperatures increases the modulus of elasticity. These results follow the trend exhibited by timber. Conclusively, Sharma et al. [11] show that although certain processing may increase the strength parameters parallel to the grain the strength of the specimen perpendicular to the grain can be decreased.

Huang et al. [12] investigate the hygrothermal properties of bamboo in comparison to standard timber used in construction. They state that the hygrothermal properties of raw bamboo had been studied in some depth. However, the parameters associated with the more widely used engineered bamboo-based panels were less established and only basic hygrothermal properties were known. Huang et al. [12] obtain bamboo parameters and compare them with reference to timber parameters widely available in databases. Their results show that bamboo is more similar to hardwood than the softwood that is most commonly used in wood-based panels. Their results show that bamboo outperforms timber in heat storage and vapour resistance. However, bamboo performs worse in terms of heat transport when compared to timber. From the results presented by Huang et al. [12], bamboo is shown to be a better option than timber in lightweight construction where the climate is hot or more temperate such as those areas where bamboo is naturally found.

The limited existing studies show the promising capabilities of engineered bamboo and how processing can be used to tailor the specimens for specific purposes. In comparison to other materials, bamboo-based products perform well in all areas. However, the specimens tested are mainly laminates, panels and boards intended to be used in surface applications and flooring. Bamboo is currently better established for such uses, with the engineering use of bamboo in load-bearing structural members still limited.

2.1.2. Research on Bamboo used as Load-Bearing Structural Members

Nurdiah [4] gathers iconic case studies for bamboo—in its raw form—to be used in the main load-bearing members of a structure. In this study, the bamboo structures clearly demonstrate their effectiveness, especially when creating organically shaped buildings in which bamboo can be curved and shaped without damage. Examples of bamboo use include schools, halls, resort hotels, restaurants, and community buildings all constructed using bamboo. Moreover, Nurdiah [4] shows how bamboo is used in these structures to construct arches, rafters, battens, purlins, pillars, and trusses in order to maintain the structural integrity of these visually appealing organic shaped structures. In addition, Nurdiah [4] puts forth evidence of the capability of bamboo as a construction material, not just in surface applications, but as part of the load-bearing mechanisms of the structure. The research by Nurdiah [4] sets forth a plentiful range of examples of the successful use of bamboo in structures. However, the research does not provide numerical data, such as the capacity of these structures under loading or the mechanical properties of the bamboo members used in their construction. In order for bamboo to become more widespread, easily standardised and accepted in the construction industry, evidence of the capabilities of bamboo has to be set forth using recognized testing and numerical modelling methodologies that give acceptable quantitative results. This will give individuals and organisations confidence as to the efficacy of bamboo for given applications.

Brink and Rush [13] provide early research into the potential of bamboo reinforced concrete, praising bamboo as a viable alternative for steel rebars as a low-cost and lightweight substitute especially useful in areas where steel is less accessible. They provided detailed designs on how to construct bamboo reinforced concrete beams, columns, slabs, and walls. Javadian et al. [14] reveal that bamboo can be used alongside more conventional materials in structures. They delve into the use of bamboo fibre reinforced composites in structural concrete, in comparison to the commonly used steel reinforcement. The work by Javadian et al. [14] provides information on the bonding between the fibres and concrete matrix in a composite form. This is significantly important as the interaction between the two is essential in composites to ensure a stable load transfer between the materials and to provide shear stress transfer at the boundary between the two materials. Li et al. [15] suggested a biomimetic interlaminar transition zone model imitating bamboo bast fibre, composed of two layers of helically wound fibre. The behaviour of the model was verified by engineering composite test models using four types of macro fibre specimens.

Mofidi et al. [3] constructed and experimentally tested bamboo-based composite structural members in compression. The composites are constructed of full- or split-culm Moso bamboo fibres, a synthetic or bio-based matrix, and surrounded by either natural hemp confinement or synthetic PVC confinement to help prevent early buckling of the specimens. Furan resin is one of the matrices, which is a bio-based carbon-neutral polymer with a number of desirable environmental-friendly properties. Cementitious grout and epoxy are also used as the studied matrices. Mofidi et al. [3] state the circular and hollow cross-section of bamboo present problems; although the circular shape performs well in flexion, it makes bamboo fibres prone to local buckling and causes problems in the development of connections at the joints between members. In order to overcome these inherent weaknesses, they state that engineered bamboo products can be manufactured to create bamboo products that have uniform sections and desirable shapes whilst maintaining the natural desirable mechanical properties. They state bamboo fibres perform well in tension having been shown to reach strengths of 1000 MPa. However, bamboo culms are susceptible to buckling in compression. For this reason, they choose to test the specimens under axial compressive loads to investigate whether the use of an engineered composite product can improve the mechanical properties under such a load case. Their results show that the bamboo composites have improved strength, absorbed energy, stiffness and ductility compared with non-composite bamboo. Mofidi et al. [3] show that the compressive strength of bamboo composites is improved by as much as 294.4% when compared with non-composite bamboo (control specimen), suggesting that when such a load case is standard, such as in columns, engineered bamboo products can be considered as a preferable choice. In

Table 1. Experimental results of Mofidi et al. [3].

Specimen	Load at Rupture (kN)	Area of Cross-Section (mm2)	End Shortening at Peak (mm)	Density of Specimen (kg/m3)	Axial Stress (MPa)	Gain (%)	Capacity Over Weight (kN/kN)
Control	152.4	2764.6	5.75	1147.3	55.1	−	12,323
FCB-EPX-I	601.1	8332.3	13.82	1174.5	72.1	294.4	15,681

, FCB-EPX-I label corresponds to the specimen made from Full Culm Bamboo and EPoXy matrix with Improved confinement level.

From the promising studies that have been conducted on engineered bamboo, it can be concluded the potentials for engineered bamboo construction are promising. However, the adoption of bamboo as a mainstream structural material requires more extensive developments and systematic research on the standardized use of engineered bamboo, which is currently lacking [16].

2.2. Background to FEA of Advanced Composites

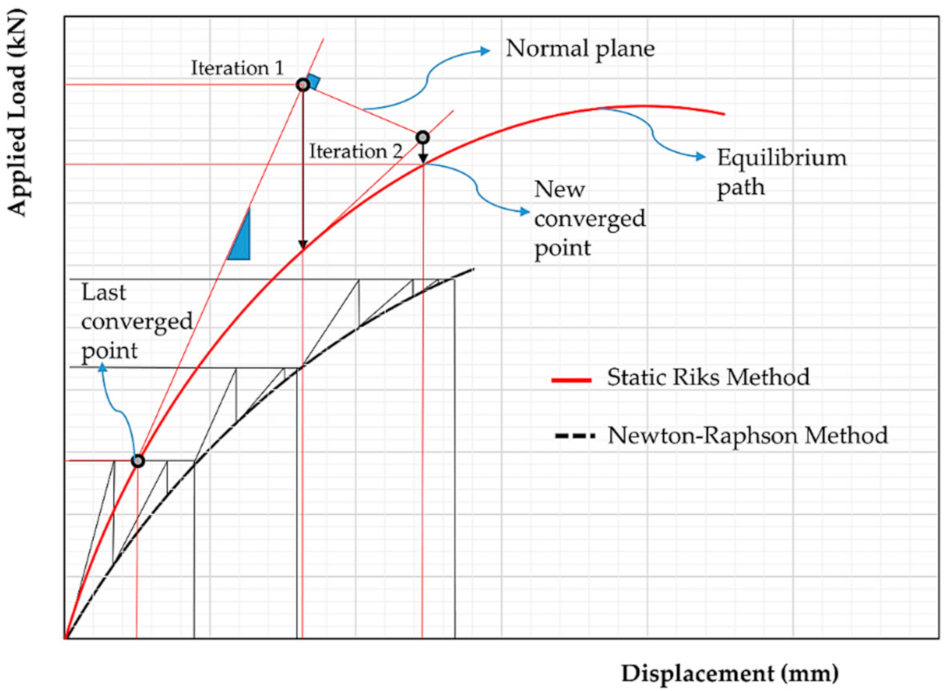
2.2.1. Static Riks Method

When carrying out a non-linear buckling analysis of an advanced composite member using ABAQUS, the use of the static Riks method is widespread [17]. This method is used when a linear buckling or eigenvalue analysis is insufficient, which is especially the case when the materials show non-linear or plastic behaviour [18]. When a structure undergoes deformation due to material plasticity before buckling occurs, parameters in the system change with deformation. An eigenvalue analysis is more suitable for problems where deformations before buckling are very small and do not deviate greatly from the initial shape of the structure [18]. The static Riks method is better adapted to solve problems where large deformations before buckling can occur, which has been modified to give non-linear static equilibrium solutions to problems that are unstable in nature [17]. Unlike in the Newton-Raphson method, the load increments are an added unknown in the static Riks method, with the static Riks method giving load magnitudes as part of the solution [19]. The Newton-Raphson method struggles in scenarios where the tangent stiffness is close to zero [20]. Therefore, it would not be able to perform well in these situations [18]. By solving for both loads and displacements, complicated load-displacement behaviour, such as the tangent stiffness changing signs, can be captured by the static Riks method. Schematic visualization of the Newton-Raphson method and static Riks method is provided in Figure 2 for separate materials.

2.2.2. Linear Buckling/Eigenvalue Analysis

In order for buckling to occur in a structural member, imperfections have to be present [21]. Therefore, an imperfection or perturbation has to be introduced into the model to achieve buckling of the specimen. In ABAQUS, there are numerous ways to do this. One of the most common procedures is to define an imperfection by superimposing multiple buckling modes that are obtained through an eigenvalue buckling analysis. Therefore, when carrying out this method, an eigenvalue buckling prediction is necessary to obtain the buckling modes required. Subsequently, the eigenvalue of a given collapse mode shape can be input as the load to the non-linear buckling analysis. ABAQUS output returns the load proportionality factor (LPF), which is a fraction of the load given as input that is required to cause failure. Therefore, using an input load that is an overestimate, such as the bifurcation point given by an eigenvalue buckling prediction, is acceptable and ensures failure.

2.2.3. Imperfection Size

Eurocode 3 [22] provides provisions regarding the imperfections that are normally present in a variety of steel sections. For the present paper, one choice of imperfection as a modelling parameter was chosen according to Eurocode 3 [22]. This corresponds to an imperfection of 1/150 for inelastic analysis. For the bamboo composite modelled in the present paper, this equates to an imperfection of 2.67 mm in relation to the first mode shape, due to the height of the specimen being 400 mm. However, steel is not used in this study, and the degree of processing of steel construction material is higher than the completely natural raw culms of bamboo used in the composite columns modelled in the present paper. This would suggest that the Moso bamboo specimens would have much larger imperfections than manufactured steel sections. Therefore, the other choices of imperfections were taken other than that suggested by Eurocode 3 [22] for steel design.

In this regard, Yu et al. [23] carried out numerical and experimental testing to determine the axial buckling behaviour of Kao Jue (Bambusa Pervariabilis) and Mao Jue (Phyllostachys Edulis or Moso) bamboo scaffolding. Their research suggests initial imperfections of $16\frac{\mathrm{Length}}{1000}$ and $8.5\frac{\mathrm{Length}}{1000}$ for Kao Jue and Mao Jue bamboo, respectively. Although Mao Jue is the Chinese name of Moso species, Kao Jue species used in Yu et al. [23] has a compressive strength closer to the Moso bamboo used by Mofidi et al. [3]. In this paper, Mao Jue designation will be used for the Moso bamboo when imperfections proposed by Yu et al. [23] are discussed. It should be noted that the suggested values of imperfection by Yu et al. [23] correspond to raw bamboo species used for scaffolding.

3. Numerical Modelling Methodology

3.1. Material Properties Used as Input

The properties of the materials given as input in an FEA are essential for accurate outputs. In some cases, these properties are published by the manufacturer. This fundamentally occurs with more widely used materials, such as steel or concrete. Otherwise, the properties can be obtained by experimental testing of the specimens beforehand. In the present research, the material properties provided by Mofidi et al. [3] were used for all the constituent parts. Certain information key to the FEA model such as Poisson’s ratio and stress-strain behaviour of epoxy, Moso bamboo, and PVC was required to be extracted by reviewing previous literature. Equations (1) and (2) proposed by Girão Coelho et al. [24] are used to convert from the measured engineering stress (σ) and engineering strain (ε), giving constitutive models that ABAQUS will be able to interpret.

$${\mathsf{\sigma }}_{\mathrm{true}}=\mathsf{\sigma }\left(1+\mathsf{\epsilon }\right)$$

(1)

$${\mathsf{\epsilon }}_{\mathrm{true}}=\ln \left(1+\mathsf{\epsilon }\right)$$

(2)

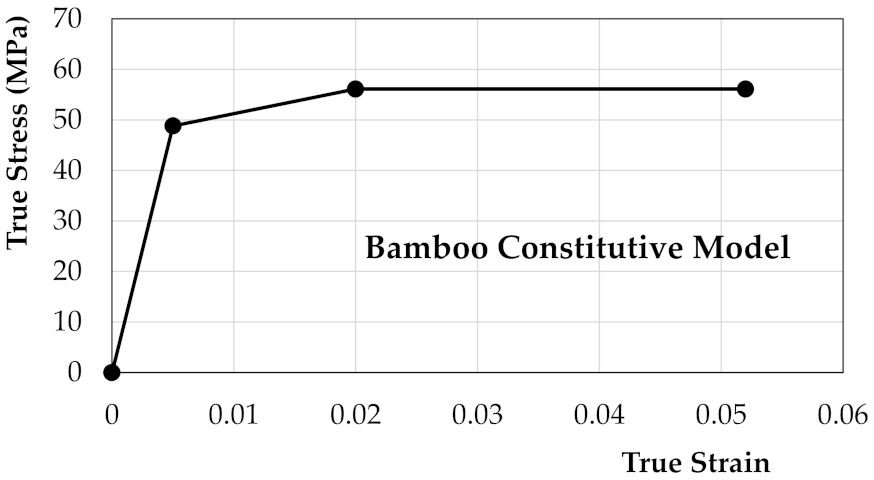
3.1.1. Moso Bamboo

Mofidi et al. [3] state the properties in compression of the bamboo are 56.1 MPa and 9.76 GPa, for the compressive strength and Young’s Modulus, respectively. Zhang et al. [25] proposed the behaviour of Moso bamboo is linear elastic until a yielding point. After the sample yields, it undergoes non-linear plastic deformations. Finally, the sample enters a linear plastic plateau portion. Li et al. [26] analysed the compressive strengths and stress-strain behaviour of Moso bamboo specimens at various growth heights. The samples Li et al. [26] used are engineered laminate bamboo with a phenol-based matrix. However, the stress-strain behaviour observed by Li et al. [26] shows the same pattern as Zhang et al. [25], which is carried out on raw Moso bamboo specimens. The advantage of the model presented by Li et al. [26] is that the Young’s Modulus taken from the linear elastic portion of the graph is much closer in magnitude to the Young’s Modulus reported by Mofidi et al. [3]. This could be due to efficient composite action between bamboo and the resin matrix in both studies. Moreover, the model presented by Li et al. [26] is an abstraction of actual results, which made the bamboo specimens stiffer than the raw bamboo specimens tested by Zhang et al. [25]. Li et al.’s [26] model is tri-linear, including a linear elastic portion followed by a linear strain-hardening portion and finally a linear plastic plateau portion. Lopez [27] carries out extensive experimental testing to determine the mechanical properties of bamboo in raw and treated form. Based on Lopez [27], the value for the Poisson’s ratio of Moso bamboo is very close to 0.3 for all treatments, with the exception of green bamboo.

In this regard, the constitutive model given as input to ABAQUS in this study (Figure 3) takes the tri-linear behaviour based on the strain at which yielding occurs, the strain at which the plastic plateau portion begins, and the strain at which failure occurs.

3.1.2. Epoxy

The epoxy resin used by Mofidi et al. [3] is a low viscosity two-part resin with 3.12 GPa flexural modulus, 123.4 MPa flexural strength, 3.18 GPa tensile modulus, 72.4 MPa tensile strength, and 86.2 MPa compressive strength. Fard [28] carries out extensive research on the non-linear inelastic mechanical properties of epoxy resins. Their research details the response of epoxy resins under a variety of loading conditions with constitutive models for the behaviour of epoxy produced. A variety of epoxy resin samples are tested including those which share similar properties to the resin used by Mofidi et al. [3]. Fard [28] states that in compression, the proportionality elastic limit (PEL) in compression is 59–66% of the compressive yield stress. For specimens presented in the tabulated results by Fard [28], with similar ultimate compressive strengths to Mofidi et al. [3], the percentage difference in PEL and compressive yield stress are on the higher end of this scale. With regard to Poisson’s ratio of epoxy, Cease [29] suggests a value of 0.36 for specimens with similar mechanical properties to the epoxy used by Mofidi et al. [3].

In the present research, the compressive yield stress is taken to be the ultimate compressive strength of 86.2 MPa, as given by Mofidi et al. [3], and the PEL is taken as 63% of this value (Figure 4).

3.1.3. PVC

The PVC used in the studied physical specimen has a modulus of elasticity and ultimate compressive strength of 7.91 GPa and 58 MPa, respectively. Yonan et al. [30] carry out experimental testing on PVC to determine its plastic behaviour and to investigate how failure occurs in PVC samples. It is now well-established that PVC firstly undergoes linear elastic deformations, followed by non-linear plastic deformations, after which softening occurs and there is a period of re-hardening up until failure. Research studies by Ognedal [31], Kendall and Siviour [32], and Alves and Martins [33] support the findings of Yonan et al. [30] and demonstrate congruent behaviour. These experimental results also show that the strain at which the linear elastic period of the curve ends is consistently at very small values (below 0.05). In terms of the strain at failure, the results presented by Alves and Martins [33] show PVC reaching a true strain as high as 0.9 before failure occurs. Additionally, Ognedal [31] reports a value of 0.3 for the Poisson’s ratio of PVC.

Accordingly, the constitutive model given as input to ABAQUS was produced (Figure 5). The model is an abstraction of their experimental results and a bilinear relation is chosen to represent the material properties. In this research, Poisson’s ratio of PVC is taken as 0.3 based on the work carried out by Ognedal [31].

3.2. Eigenvalue Buckling Analysis

In the present work, a non-linear buckling analysis was carried out due to the materials of interest exhibiting non-linear behaviour and showing material plasticity. In such a case, a linear buckling analysis is not appropriate and a non-linear analysis using a method, such as static Riks, is better suited to achieve accurate results [19]. However, in order to carry out a non-linear buckling analysis, imperfections need to be introduced into the modelled specimen. If this step is not carried out, buckling will not occur. An eigenvalue buckling analysis was therefore undertaken. The collapse mode shapes given by the linear buckling analysis were used in defining the imperfections in the non-linear buckling analysis. Imperfections were defined by superimposing multiple buckling modes, meaning an imperfection corresponding to each of the calculated collapse mode shapes can be introduced into the model. For the present research, imperfections corresponding to the first mode shape were taken and introduced into the model. This offered realistic results, allowing for a comparison between the tested imperfections, taken from different sources, and simplified the model.

In terms of how the model was assembled, the specimens made in ABAQUS were based entirely on the composite proposed by Mofidi et al. [3], with an epoxy matrix, full culm Moso bamboo fibres, and a PVC confinement. The dimensions, orientations, and arrangement of parts in the ABAQUS model were all based on the information presented in their study. This is shown in Figure 1 and Figure 6, which indicate the experimental samples constructed by Mofidi et al. [3] and the samples made in ABAQUS for the present paper, respectively.

When defining the material properties, only the linear elastic behaviour of epoxy, Moso bamboo, and PVC were given as input to the model at this stage. The constitutive models proposed (Figure 3, Figure 4 and Figure 5) were only introduced into the model when carrying out the non-linear buckling analysis as these models describe more complex behaviour (i.e., material plasticity).

In addition, a linear perturbation buckling step was implemented. This step is primarily suitable for linear problems and therefore only used for the linear buckling analysis. In some cases, a linear perturbation is used to determine the eigenvalues and collapse mode shapes of a system [34]. It should be noted that only the first collapse mode shape was used when defining the imperfections in the non-linear analysis. Figure 7 is an example of the first five mode shapes that were calculated.

The bottom face of the composite column was constrained so that displacements could not occur in any direction and rotations were not permitted about any axis. For the top face where the load was applied, only displacements in the z-direction (axial direction) were allowed (as shown by the coordinate system in Figure 6), with all other displacements and rotations set to zero. For the loading, a uniformly distributed pressure across the top face of the column and acting in the axial direction was applied to mimic the experimental methodology used by Mofidi et al. [3].

3.3. Contact/Interaction

In ABAQUS, the interaction between parts must be defined. For the model described in the present paper, the interaction between the full culm Moso bamboo fibres and epoxy matrix needed to be given as input. It was not necessary to define the interaction between the epoxy matrix and PVC confinement, as they were modelled using a single part with separate material definitions on either side of the face that represented the boundary between the two. For the interaction between the fibres and matrix, there were a number of options provided by ABAQUS. In general, the fibres could either be embedded within the matrix, which represents an ideal scenario where the bonding between the two is perfect and no slipping can occur, or the bond behaviour can be specified as input, using data from the bond-slip behaviour between the two materials [17]. For the present paper, the fibres were embedded within the matrix.

3.4. Mesh Refinement and Element Types

Due to the geometry of the bamboo composite modelled in the present paper, a three-dimensional FEA was carried out. With a two-dimensional model, abstractions would have had to be made in order to represent the three-dimensional problem, producing results that were less accurate and harder to analyse [35]. The chosen elements also had to reflect the geometry and behaviour of the bamboo composite being modelled; therefore, 3D solid elements were mostly used. However, shell elements were also experimented with for the full culm bamboo fibres, as they are hollow and their 2.5 mm thickness is relatively small compared with their 400 mm length. As stated by Sadowski and Rotter [36], the dimensions are relevant. When the thickness of an element is small in comparison to its length, behaviours such as transverse shear deformation, which cannot be effectively captured by shell elements, are less important [36]. Additionally, shell elements are much less computationally expensive [37] making them a desirable alternative to costly 3D solid elements when the situation allows for their use. S4R shell elements were used for the fibres to test their efficacy. These general-purpose shell elements can account for transverse shear deformations when the shell is thick—according to thick shell theory—and when the shell is thin and transverse shear is not a concern, the elements become discrete Kirchhoff thin shell elements [38]. The reduced integration version of the element is used as shell elements can undergo locking, wherein the stiffness can get too large. Using reduced integration can soften the elements and thus account for this problem. For the solid elements, the three-dimensional eight-node linear brick element was implemented (C3D8), with the version of the element with reduced integration (C3D8R) also being used. For the C3D8R element, hourglass control was included to ensure the element did not become excessively flexible.

H-version mesh refinement was used to allow convergence of the outputs given by the FEA. This was done by progressively increasing the density of the mesh seeds applied to each part in the model, prior to the mesh being generated. This in turn made the mesh finer, as the seeds control how coarse the mesh is in any given region. With finer meshes, the accuracy of the solution is expected to improve up until a given threshold, at which increasing the mesh density yields no significant change in the output given. At this point, convergence has occurred, and further refinements are not necessary.

3.5. Non-Linear Buckling Analysis Using Static Riks Method

For the non-linear buckling analysis, the model used in the eigenvalue buckling analysis was replicated with a number of changes made to the material definitions, the load applied, and steps. Additionally, imperfections were added to the model at this stage. In terms of the material definitions, plastic behaviour was added to the model in conjunction with the elastic behaviour defined in the eigenvalue buckling analysis. The constitutive models (Figure 3, Figure 4 and Figure 5) were given as input by entering the tabulated stress-strain data into ABAQUS. The load applied was still a uniform pressure load at the top face acting in the axial direction. However, the magnitude of this load was changed to be the eigenvalue of the first collapse mode shape. The step used in the non-linear buckling analysis was as per the static Riks method, with non-linear geometry enabled. This step is used due to the static Riks method excelling in buckling problems, especially where deformations of the specimen before buckling and material nonlinearity are present, e.g., [17,18,19] as was the case for the composite column modelled in the present paper. Imperfections were added corresponding to the first collapse mode shape. Three imperfections were used, and the respective results obtained were compared. As an imperfection for the exact physical tested specimen was not available, imperfections given for similar section shapes or materials were used to give a good approximation. As mentioned earlier, Yu et al. [23] suggest imperfections based on their research of full culm bamboo scaffolding. They suggest imperfections of $16\frac{\mathrm{Length}}{1000}$ and $8.5\frac{\mathrm{Length}}{1000}$ for Kao Jue and Mao Jue bamboo, respectively. In addition, Eurocode 3 [22] gives a recommended imperfection of 1/150 of the height for plastic analysis of a solid cylindrical steel section. This corresponds to an imperfection of 2.67 mm for the 400 mm composite modelled in the present paper. In this study, the FEA was run with the 6.40 mm, 3.40 mm, and 2.67 mm imperfections corresponding to the Kao Jue culm, the Mao Jue culm, and the Eurocode 3 solid cylindrical steel section, respectively. These imperfections were implemented separately during different runs of the FEA so that the efficacy of each could be established and suggestions could be made with regard to the size of imperfection that should be used in future models.

4. Results and Discussion

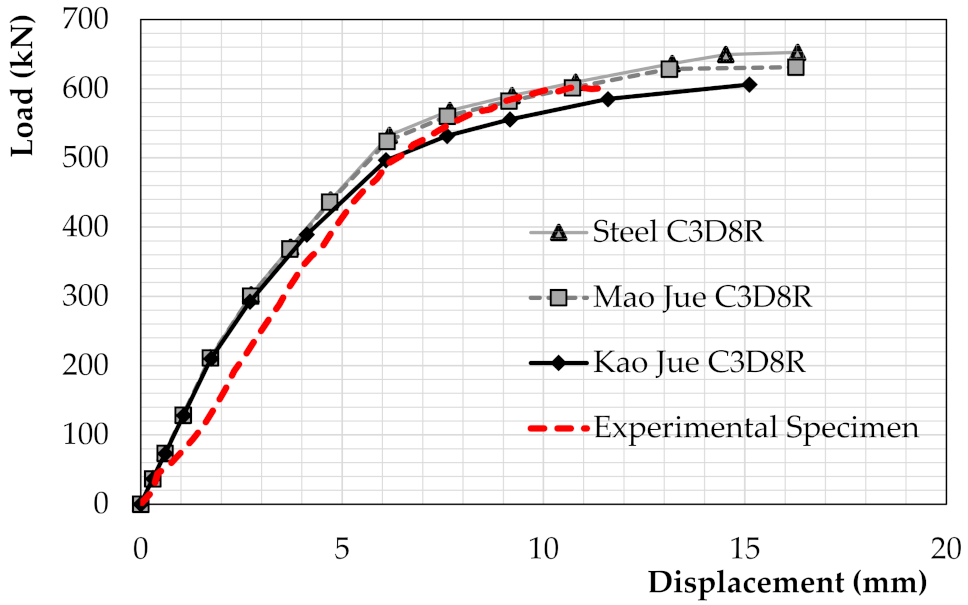
4.1. Load-Displacement Behaviour

Figure 8 shows the physical specimen after failure (Figure 8a) and the load-displacement behaviour of the physical specimen, labelled FCB-EPX-I (Figure 8b). It can be seen that the output from the FEA (Figure 9) describes a very similar shape to the experimental results. The behaviour is initially linear elastic, followed by a hardening section wherein non-linear plastic deformations occur.

The hardening period given by the FEA is larger than that of the experimental curve. The curve given by the experimental results exhibits linear elastic behaviour up to higher stresses than is shown by the curves given by ABAQUS. The graphs produced by the FEA exhibit non-linear behaviour much sooner and seem to describe more ductile behaviour. This occurs irrespective of the elements or imperfections used. However, it is likely as a result of the constitutive models given as input (Figure 3, Figure 4 and Figure 5).

In terms of the load at buckling and the axial displacement at buckling, the FEA predicted results that were in general precise and close to the experimental results. However, this was contingent on the imperfections used and element types implemented.

4.2. Effect of Using Different Imperfection Sizes

In this section, the outputs of the FEA models with different imperfection sizes are compared with each other and to the experimental results. The load-displacement and stress-strain behaviour—for all three imperfection sizes (6.4 mm, 3.4 mm, and 2.67 mm)—are shown in Figure 9 and Figure 10, respectively, with C3D8R elements being solely used for all so as to ensure an accurate comparison. As can be seen in Figure 9, the load-displacement behaviour generally stays the same with no major deviations in shape observable. This is also the case for the stress-strain behaviour, where the trends observed stay the same irrespective of the size of the imperfection. However, the ultimate load reached by the specimen before buckling changes significantly depending on the size of the imperfection introduced (

Table 2. Outputs given by the FEA for varying imperfection sizes and element types caused minor changes in the ultimate load behaviour.

Element Used	Imperfection (mm)	Load at Rupture (kN)	Axial Displacement at Rupture (mm)	Axial Stress at Rupture (MPa)
C3D8R	2.67	652.4	16.31	73.93
C3D8R	3.40	631.2	16.26	71.52
C3D8R	6.40	606.0	15.11	68.67
C3D8	2.67	655.3	15.49	73.55
C3D8	3.40	645.4	15.41	73.13
C3D8	6.40	607.2	15.26	68.80
C3D8R + S4R	3.40	650.8	14.01	73.74

). The loads at rupture are 606.0 kN, 631.2 kN, and 652.4 kN for the Kao Jue, Mao Jue and steel imperfections, respectively. This indicates that as the size of the imperfection increases, the ultimate load before buckling decreases. This is expected as imperfections in a member are necessary to cause buckling. This implies that in the modelled specimens, the larger the imperfections in a specimen, the more susceptible it is to buckling, which makes sense physically. For relatively small changes in the size of the imperfections introduced, large changes in the ultimate load capacity of the member occur. For instance, the Mao Jue imperfection is just 0.73 mm larger than the steel imperfection, and this results in a 21.2 kN difference in the load at rupture. This suggests that an accurate approximation of the imperfections present in a specimen is key to obtaining realistic results when carrying out a buckling analysis in FEA software. In terms of the axial displacement of the specimens at rupture, the results are relatively similar for all imperfections. The axial displacement at buckling is 15.1 mm, 16.3 mm, and 16.3 mm for Kao Jue, Mao Jue, and steel imperfections, respectively (Table 2). These are only small deviations, with the values either changing slightly or not at all.

In terms of the axial stress at buckling, the values given by the FEA are 68.7 MPa, 71.5 MPa, and 73.9 MPa for the Kao Jue, Mao Jue, and steel imperfections, respectively (Figure 10). In the experimental testing of the bamboo-based composites, the load at rupture was 601.1 kN, corresponding to axial stress of 72.1 MPa, with an axial displacement at buckling of 14.1mm. At first glance, it seems that the Kao Jue specimen with the C3D8R elements gives the best results when compared to the experimental results. This is due to the load at rupture given as output being so close to the experimental value (606.0 kN for the FEA as compared to the experimental value of 601.1 kN). However, the specimen modelled using the Mao Jue imperfection and C3D8R elements gives results closest to the experimental values, with the axial stress at buckling differing by only 0.6 kN with the experimental result (71.5 MPa for the FEA output as compared to an experimental result of 72.1 MPa).

4.3. Effect of Using Different Element Types

As the Mao Jue imperfection gave the most accurate prediction of axial stress at buckling when using C3D8R elements, the same imperfection is compared (but using different element types) to see how this can change the outputs given (Figure 11).

The general behaviour of the specimens does not change drastically with the altering of the elements used. The same linear elastic behaviour followed by a non-linear hardening period is shown in all curves. In general, the FEM is known to be overly stiff giving deflections that are too small. For the results presented in Figure 11, the axial displacement at buckling with reduced integration is 16.3 mm and is 15.4 mm when using the same element without reduced integration. Therefore, the results would agree with the effect of implementing reduced integration elements in that the stiffness of the specimen increases leading to smaller displacements. In terms of the axial stress at buckling, the C3D8R element specimen gives a value of 71.5 MPa, the C3D8 element specimen predicts a value of 73.1 MPa, and the specimen using C3D8R and S4R elements returns a value of 73.7 MPa (Table 2).

Therefore, using the C3D8R elements produces a value marginally closer to the experimental value of 72.1 MPa. As the results make apparent, the use of shell elements leads to results that are not orders of magnitudes different from the values obtained using solid elements. In addition, the use of shell elements leads to the most accurate prediction of axial displacement at buckling (14.0 mm as compared to an experimental value of 14.1 mm). It appears that the use of shell elements has multiple benefits, mainly associated with the reduction in computation time when running the FEA as expected.

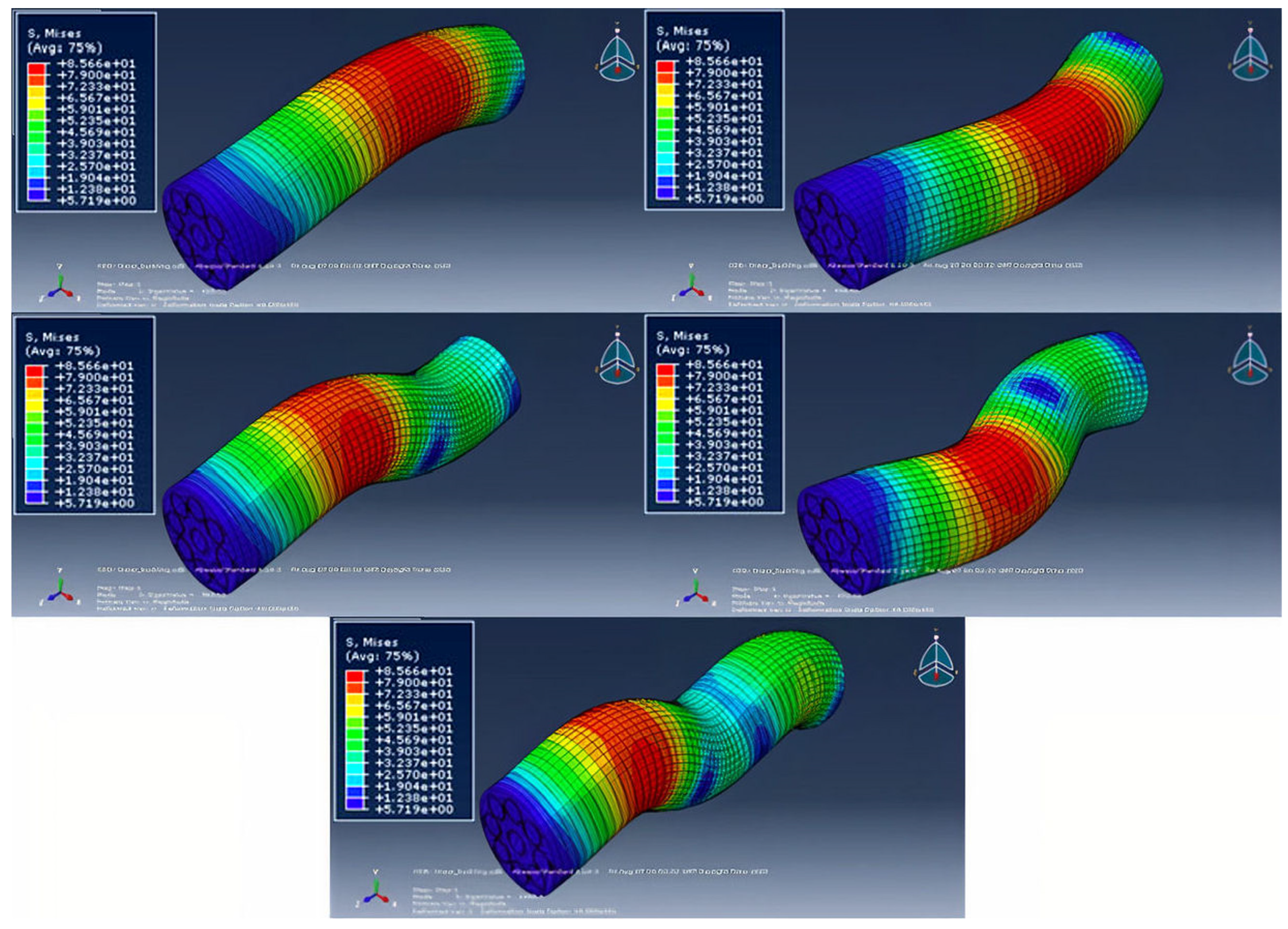
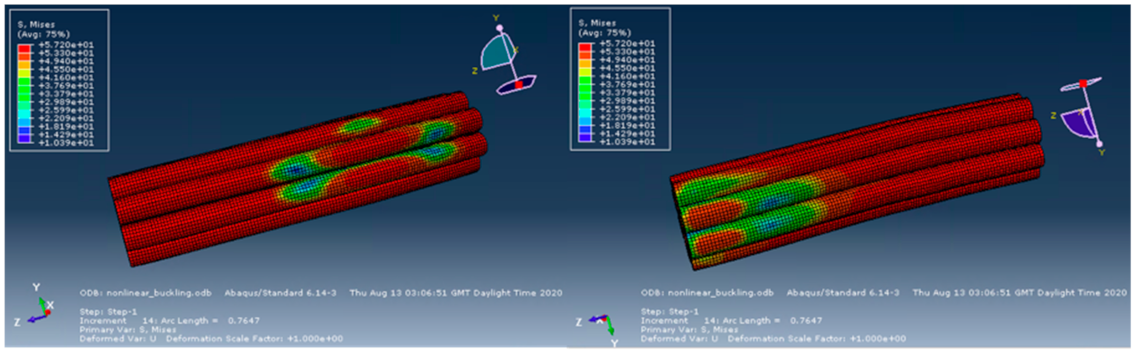
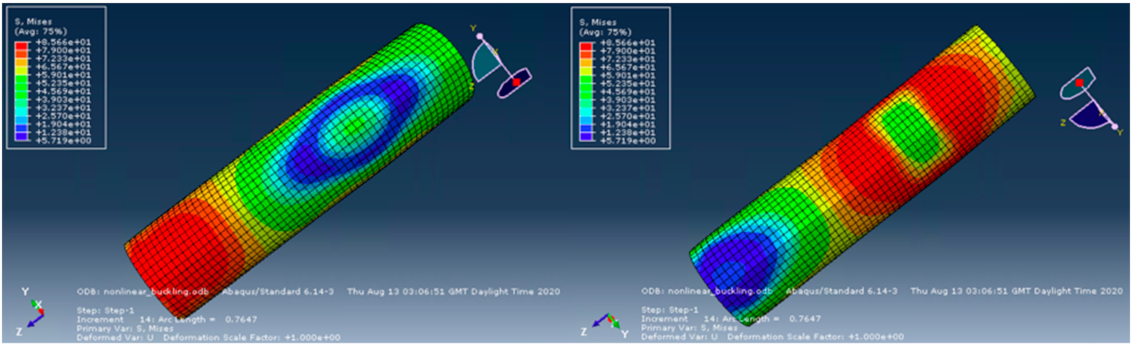
4.4. Stress Distributions

In the section, the Von Mises stress as displayed by ABAQUS is compared for each of the constituents of the composite (Figure 12). The purpose of this is to show the areas with the largest stress concentrations. Therefore, it can be observed whether the stress distribution correlates with the failure mode of the physical specimen. Additionally, modifications can be made to strengthen these areas in future optimisations of the design of the composite.

In Figure 13, the red areas in the display correspond to the largest magnitudes of stress in Moso fibres. High stresses can be visualised throughout the fibres (Figure 13), with the stress being almost uniform throughout the part. In terms of the matrix, the stress distribution is more complex and variable (Figure 14).

A stress concentration can be visualised at the base of the specimen (left image, Figure 14). An additional location that experiences a large stress concentration is close to the midspan, where large lateral displacements of the column occur (the red region visible in the image on the right of Figure 14).

For the confinement (Figure 15), the stresses are much smaller throughout than for the fibres or matrix with the orange region (right image, Figure 15) being the area of greatest stress. This area corresponds to the part of the column that undergoes large lateral displacements at buckling. However, the stress concentration experienced in the confinement is of a smaller magnitude than those visible in the other parts. Furthermore, the stress is moderately uniform throughout the PVC.

The stress distributions would suggest that the fibres are at greatest risk due to the large stresses those areas experience throughout. In addition, the Moso bamboo fibres have the smallest compressive strength out of the constituent parts. The combination of a large amount of stress being concentrated in the fibres and the material exhibiting less desirable properties than the matrix and confinement under axial compressive loads would suggest failure is likely to occur at this location. The failure described by the physical specimen (Figure 8a) shows that the bamboo fibres have indeed failed at the upper parts of the culms where the load was applied. This supports the conclusions drawn from the stress distribution, as presented by the software.

5. Conclusions

A bamboo-based composite column that reached a promising compressive strength of 72.1 MPa in separate studies by this group was numerically modelled and analysed using ABAQUS software. Due to the lack of previous similar studies in the literature, separate non-linear numerical models with different modelling parameters were evaluated to find the most accurate approach in modelling such specimens. Based on the results of the current research study, the following major conclusions can be drawn:

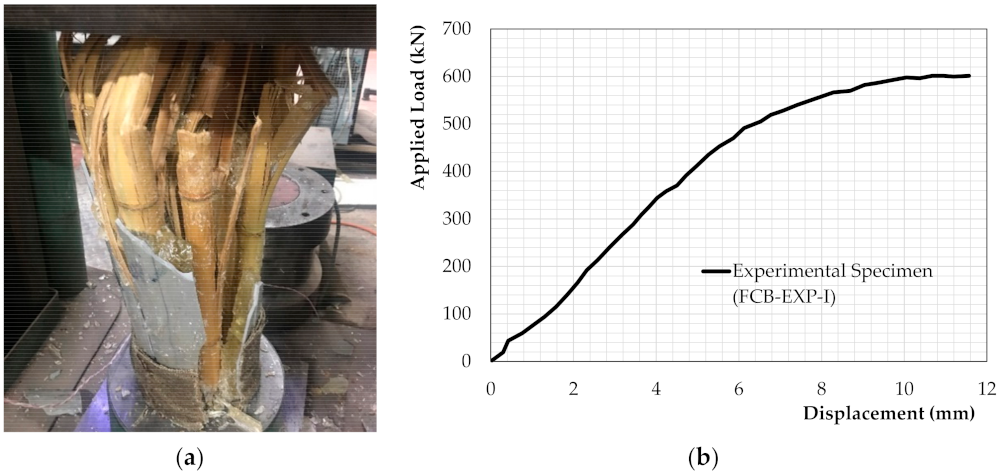
• The experimental results published by this group were supported by the FEA carried out in the present paper. The impressive load at rupture of the physical specimens (601.1kN) was either equalled or slightly exceeded by the results given by the numerical models. This confirmed the large increase in the compressive resistance of the composite member as compared to raw bamboo.
• When comparing the imperfections used for the composite bamboo models, those designed for raw bamboo work optimally as opposed to the steel imperfections based on Eurocode 3 that were also evaluated. In particular, the imperfection designed for raw Mao Jue bamboo gave results that were exceptionally close to the experimental values of load and axial deflections at rupture.
• Solid elements with reduced integration were shown to give results marginally closer to the experimental results as compared with identical elements without reduced integration.
• Shell elements were found to be sufficient when modelling the full culm Moso bamboo fibres in the model, producing outputs that were in line with the values given using solid elements. Shell elements produced the most precise prediction of axial displacement at failure.
• The stress distributions obtained by the software showed large stresses particularly in the fibres, with the matrix subject to high stress concentrations only at certain locations, and the confinement experiencing relatively moderate stresses throughout the part. This suggests that fibres that can withstand large axial compressive loads are essential to prevent failure of the composite as a whole. Bamboo performs considerably well in this role, creating advanced composites that perform exceptionally well under compressive loads, whilst being sustainable and having a low environmental impact.