Shear Strengthening with a Fiber-Reinforced Cementitious Matrix of Reinforced Concrete Elements Under Different Levels of Loads: An Experimental Investigation
Abstract
1. Introduction
2. Materials and Methods
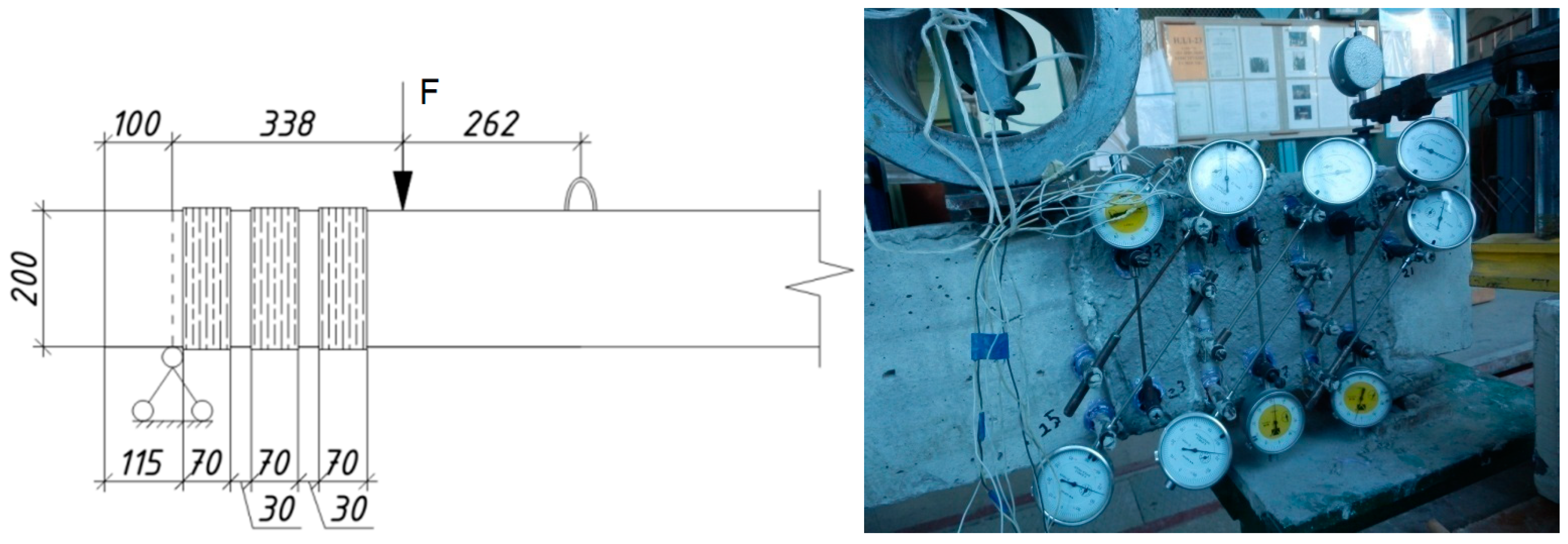
2.1. Construction of the Testing Samples
2.2. Materials
2.3. Methodology of Applying the Strengthening System
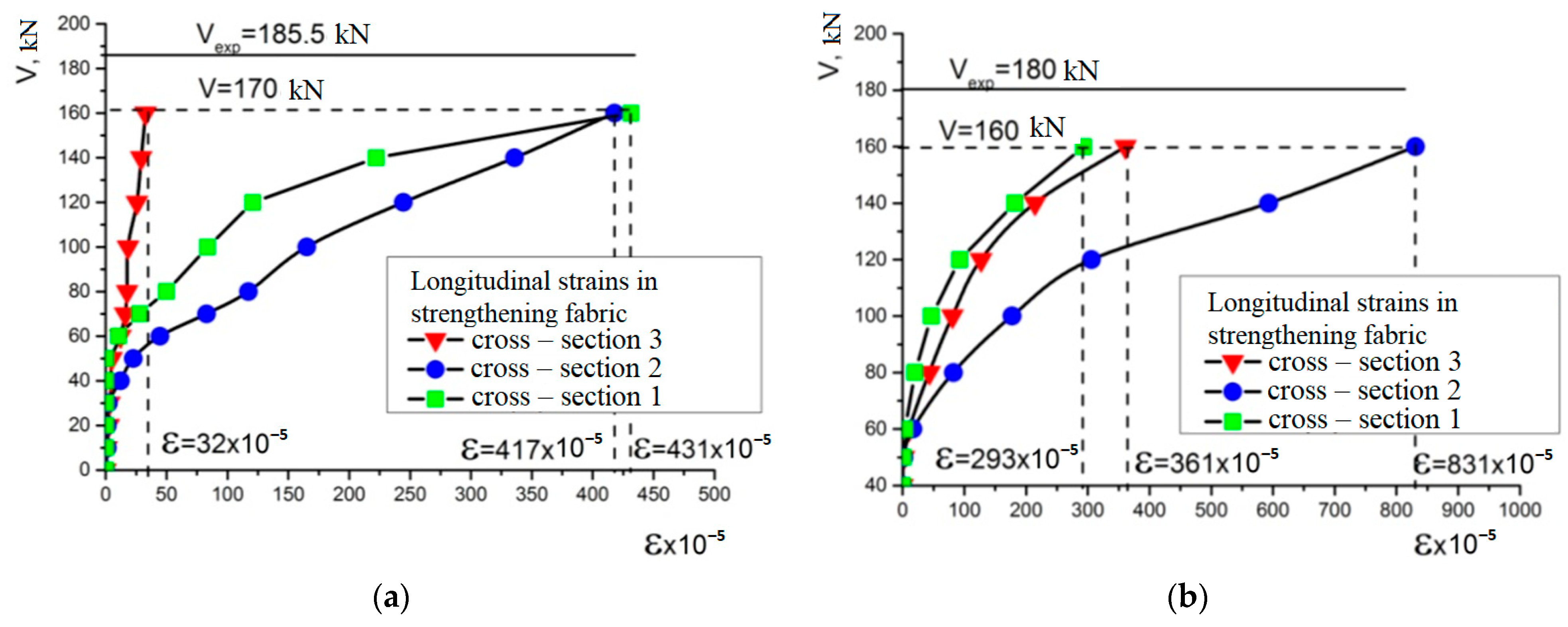
3. Results of the Experimental Testing
3.1. Bending Capacity of Testing Beams
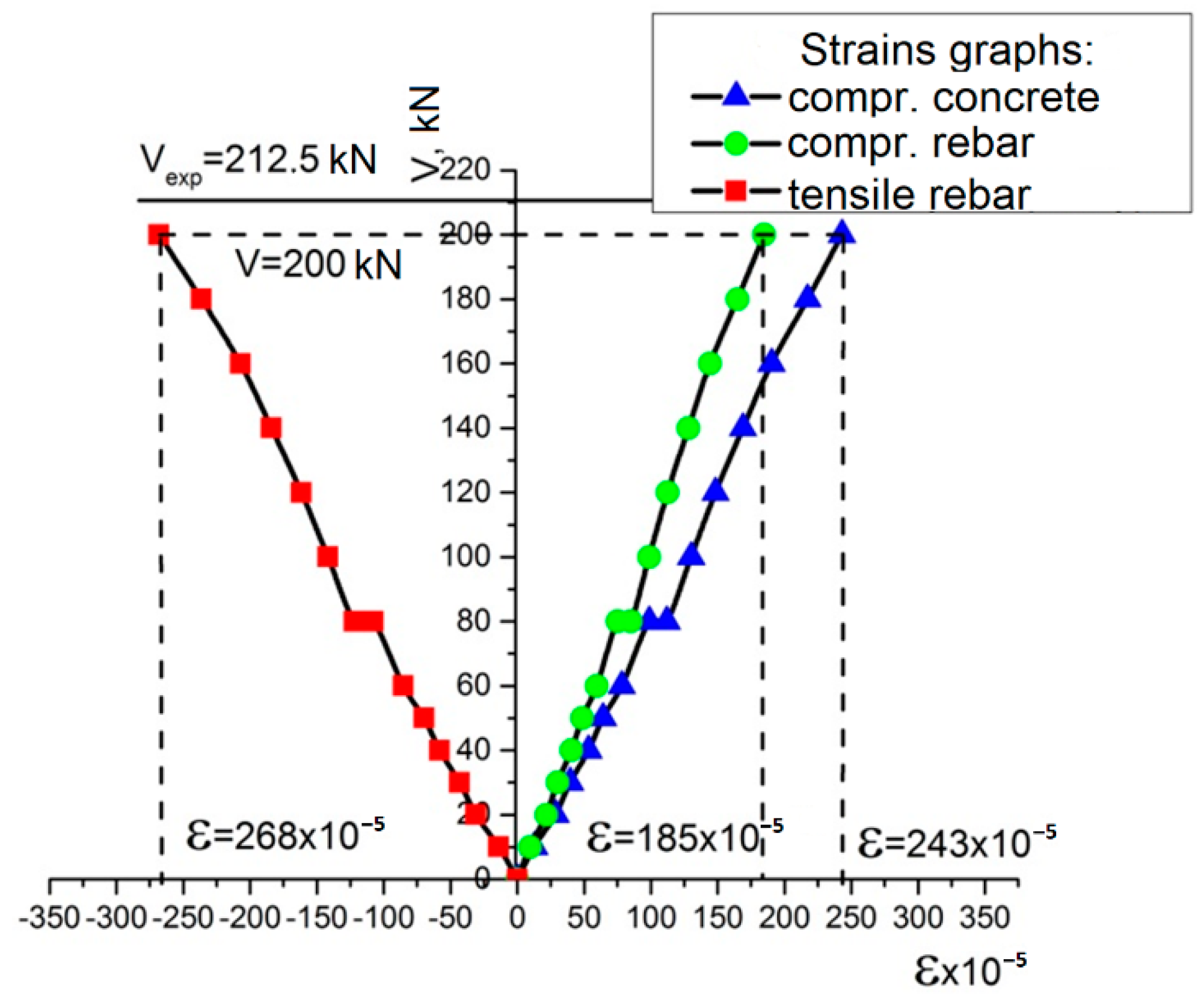
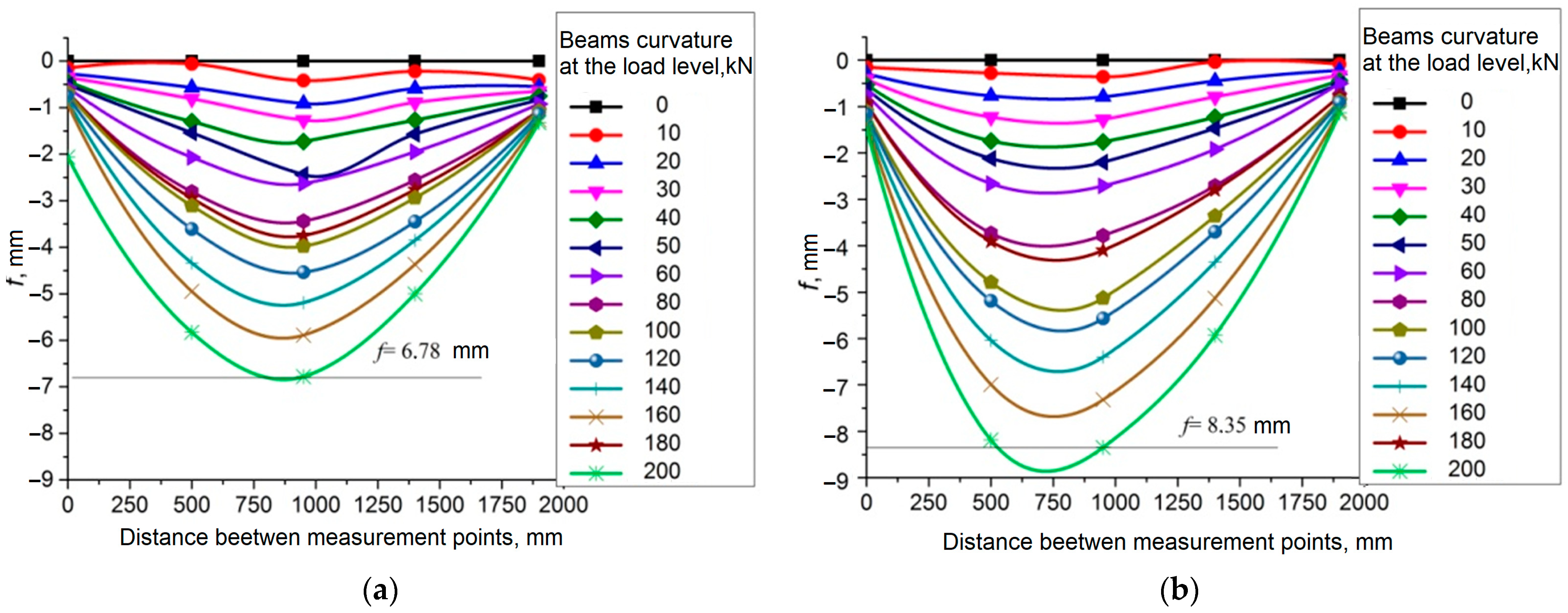
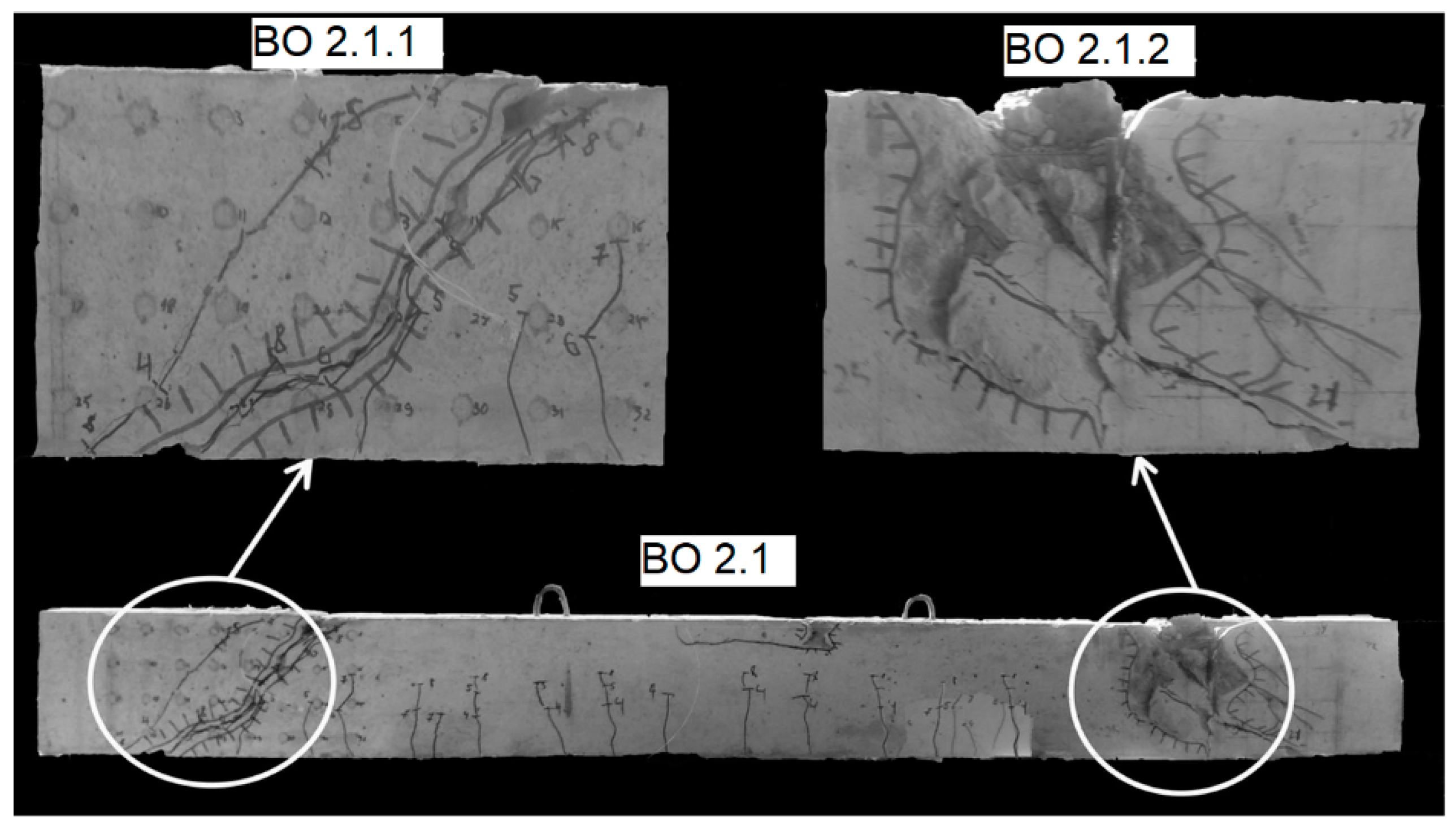
3.2. Experimental Research of Control Samples on the Shear
- The formation of an inclined crack with a critical width (acrc = 0.4 mm) on the surface of the concrete.
- The propagation of the inclined crack into the compressed concrete zone and the appearance of a crack network with an opening width of acrc = 0.05…0.2 mm on the surface of the strengthening system.
- The failure of the concrete in the inclined section in the zone of the principal tensile stresses and the delamination of the strengthening system in this area.
- The plastic deformation of the transverse reinforcement and failure of the concrete in the compressed zone, with significant deformations in the strengthening fabric, which could be visually observed due to the disruption of the protective layer.
4. Discussion
5. Conclusions
- It is worth noting the change in the nature of the failure of reinforced concrete beams under shear, which became smoother and more predictable, without the detachment of damaged particles. This indicates the effectiveness of using composite systems for strengthening reinforced concrete structures and improving their operational safety.
- The use of the strengthening tape in this study resulted in a 40% increase in the shear capacity of reinforced concrete beams, which is a satisfactory outcome.
- When strengthening reinforced concrete beams with external reinforcement equivalent to the internal reinforcement section and reducing the spacing of the transverse reinforcement by half, the bearing capacity of the inclined section increases by 25%.
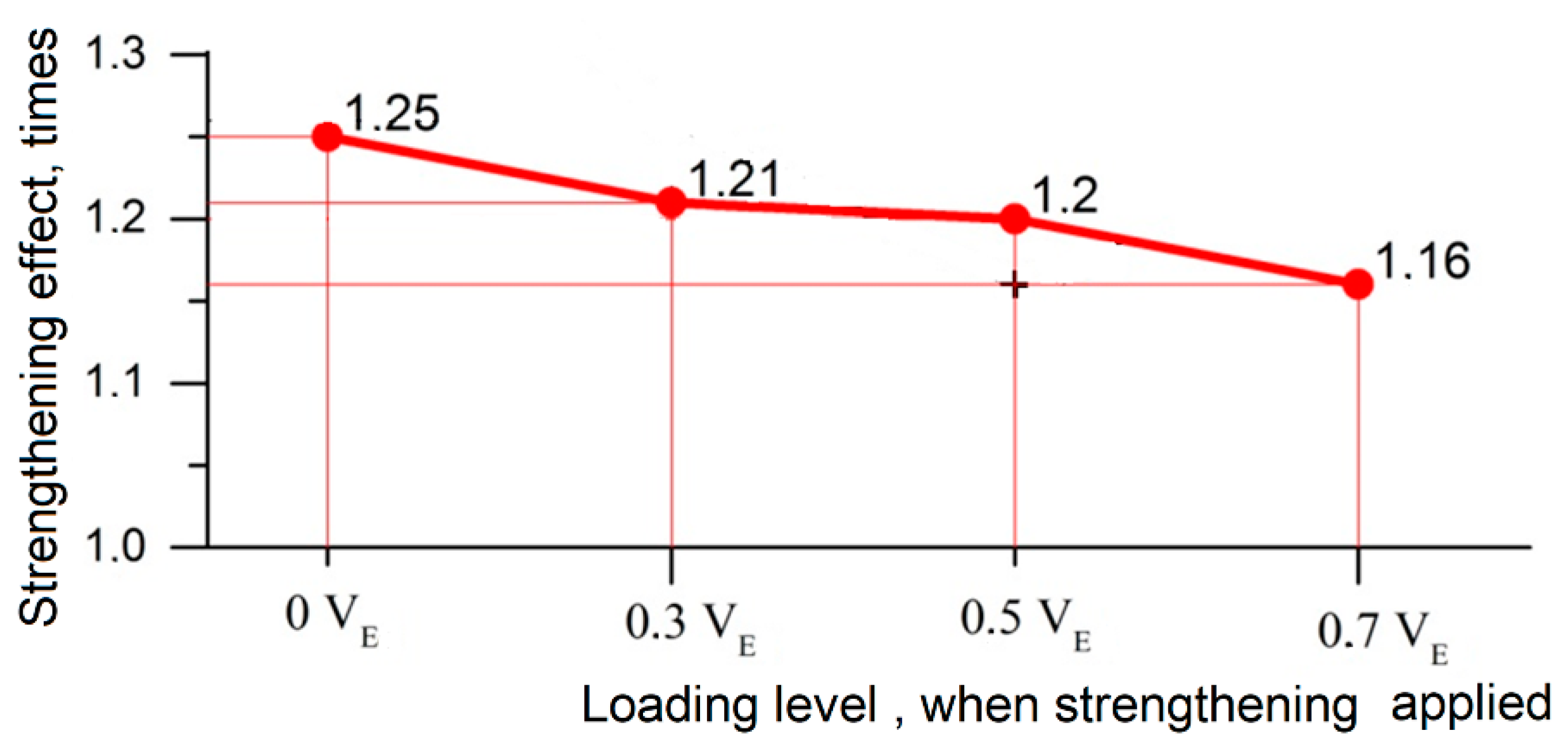
- The load level at which the strengthening is performed significantly affects the increase in the bearing capacity, reducing it to near 40% when the load level on the structure is 70% of its maximum capacity.
- For every 10% increase in the load level at which the strengthening is carried out, the maximum strengthening effect achievable by this system should be reduced by 5%. This dependency should be considered for future work at other load levels.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khmil, R.; Blikharskyy, Z.; Vegera, P.; Kopiika, N. Bearing capacity of reinforced concrete beams with and without damages of rebar. Prod. Eng. Arch. 2023, 29, 298–303. [Google Scholar] [CrossRef]
- Kopiika, N.; Vegera, P.; Vashkevych, R.; Blikharskyy, Z. Stress-strain state of damaged reinforced concrete bended elements at operational load level. Prod. Eng. Arch. 2021, 27, 242–247. [Google Scholar] [CrossRef]
- Vegera, P.; Vashkevych, R.; Blikharskyy, Y.; Khmil, R. Development methodology of determinating residual carrying capacity of reinforced concrete beams with damages tensile reinforcement which occurred during loading. East.-Eur. J. Enterp. Technol. 2021, 4, 6–17. [Google Scholar] [CrossRef]
- Klymenko, Y.; Polianskyi, K.; Grynyova, I.; Borzovič, V. Influence of Damage in the Compressed Zone of Concrete on the Bearing Capacity Along Inclined Sections and Crack Formation Characteristics. Lect. Notes Civ. Eng. 2024, 604, 225–234. [Google Scholar] [CrossRef]
- Šarvaicová, S.; Borzovič, V.; Halvonik, J. Experimental investigation of punching shear behavior of flat slabs supported by rectangular columns and loaded with various load patterns. Struct. Concr. 2024, 25, 1404–1417. [Google Scholar] [CrossRef]
- Selejdak, J.; Bobalo, T.; Blikharskyy, Y.; Dankevych, I. Mathematical modelling of stress-strain state of steel-concrete beams with combined reinforcement. Prod. Eng. Arch. 2023, 29, 108–115. [Google Scholar] [CrossRef]
- Vegera, P.; Borzovic, V.; Blikharskyi, Z.; Khmil, R. Experimental data of RC beams shear strength with different shear span and strengthening by FRCM system. Web Conf. 2024, 550, 01007. [Google Scholar] [CrossRef]
- Blikharskyy, Y.; Khmil, R.; Selejdak, J.; Katunský, D.; Tytarenko, R.; Blikharskyy, Z. Crack Resistance of RC Columns Strengthened By CFRP Under 30% of Uls Loading. Syst. Saf. Hum.-Tech. Facil.-Environ. 2023, 5, 36–45. [Google Scholar] [CrossRef]
- Feng, R.; Tang, J.P.; Wang, F.; Wang, S.; Zeng, J.J.; Zhu, J.H. Experiments on shear behavior of reinforced concrete continuous beams strengthened by C-FRCM. Struct. Concr. 2024, 25, 1052–1075. [Google Scholar] [CrossRef]
- Gemi, L.; Alsdudi, M.; Aksoylu, C.; Yazman, Ş.; Özkılıç, Y.O.; Arslan, M.H. Optimum amount of CFRP for strengthening shear deficient reinforced concrete beams. Steel Compos. Struct. 2022, 43, 735–757. [Google Scholar] [CrossRef]
- Zapris, A.G.; Kytinou, V.K.; Gribniak, V.; Chalioris, C.E. Novel approach for strengthening T-beams deficient in shear with near-surface mounted CFRP ropes in form of closed stirrups. Dev. Built Environ. 2024, 18, 100394. [Google Scholar] [CrossRef]
- Taie, B.; Mandor, A.; El Refai, A. Experimental and numerical investigation of two–span RC beams strengthened with fiber–reinforced cementitious matrix (FRCM). Eng. Struct. 2024, 300, 117246. [Google Scholar] [CrossRef]
- Mendizabal, V.; Martínez, B.; Bernat-Maso, E.; Gil, L. RC beams strengthened with hemp-FRCM and cotton-FRCM under cyclic bending loads. Eng. Struct. 2024, 318, 118718. [Google Scholar] [CrossRef]
- Teixeira, F.P.; de Souza, F.R.; Garcia SL, G.; de Andrade Silva, F. Strengthening and repair of RC beams using natural sisal Fabric-Reinforced Cementitious Matrix composite. Constr. Build. Mater. 2024, 447, 138047. [Google Scholar] [CrossRef]
- Jung, C.; Seo, Y.; Hong, J.; Heo, J.; Cho, H.C.; Ju, H. Experimental Study on Shear Strengthening of Reinforced Concrete Beams by Fabric-Reinforced Cementitious Matrix. Materials 2024, 17, 4336. [Google Scholar] [CrossRef] [PubMed]
- Calabrese, A.S.; Colombi, P.; D’Antino, T. Fatigue and post-fatigue behavior of FRCM-concrete specimens under direct shear and bending conditions. Compos. Struct. 2024, 341, 118129. [Google Scholar] [CrossRef]
- Focacci, F.; D’Antino, T.; Carloni, C. Simplified Procedure to Determine the Cohesive Material Law of Fiber-Reinforced Cementitious Matrix (FRCM)–Substrate Joints. Materials 2024, 17, 1627. [Google Scholar] [CrossRef] [PubMed]
- DSTU 3760:2006; Rolled Rebar for Reinforced Concrete Structures. General Technical Conditions: National Code of Ukraine. Institute of Ferrous Metallurgy of the National Academy of Sciences of Ukraine: Dnipro, Ukraine, 2006; 28p. Available online: https://td-slavsant.com/wp-content/gst/arm/dstu-3760-06.pdf (accessed on 16 November 2024).
- DSTU B V.2.7-217:2009; Methods of Determining Prism Strength, Modulus of Elasticity and Poisson’s Ratio: National code of Ukraine. Ministry of Construction Region of Ukraine: Kyiv, Ukraine, 2010; 20p. Available online: https://dbn.co.ua/load/normativy/dstu/5-1-0-1089 (accessed on 16 November 2024). (In Ukrainian)
- EN 1992-1-1; Eurocode 2: Design of Concrete Structures—Part 1-1. General Rules for Buildings: Brussels, Belgium, 2004. Available online: https://www.phd.eng.br/wp-content/uploads/2015/12/en.1992.1.1.2004.pdf (accessed on 16 November 2024).
- DBN V.2.6-98:2009; Concrete and Reinforced Concrete Structures: National code of Ukraine. Ministry of Construction Region of Ukraine: Kyiv, Ukraine, 2011; 68p. Available online: https://e-construction.gov.ua/laws_detail/3200410998024438840?doc_type=2 (accessed on 16 November 2024). (In Ukrainian)
- Ruredil Spa Technical Department. Instruction for the Planning of Static Consolidation Interventions Through the Use of Fibre Reinforced Cementitious Matrix; FRCM: Milan, Italy, 2008; 201p. [Google Scholar]
- Alzate, A.; Arteaga, A.; de Diego, A.; Cisneros, D.; Perera, R. Shear Strengthening of Reinforced Concrete Members with CFRP Sheets. Mater. Construcción 2013, 63, 251–265. [Google Scholar]
- Halvonik, J.; Borzovič; V; Lániova, D. Comparison of shear behaviour of concrete beams reinforced with GFRP bars and steel bars. Structures 2022, 43, 657–668. [Google Scholar] [CrossRef]

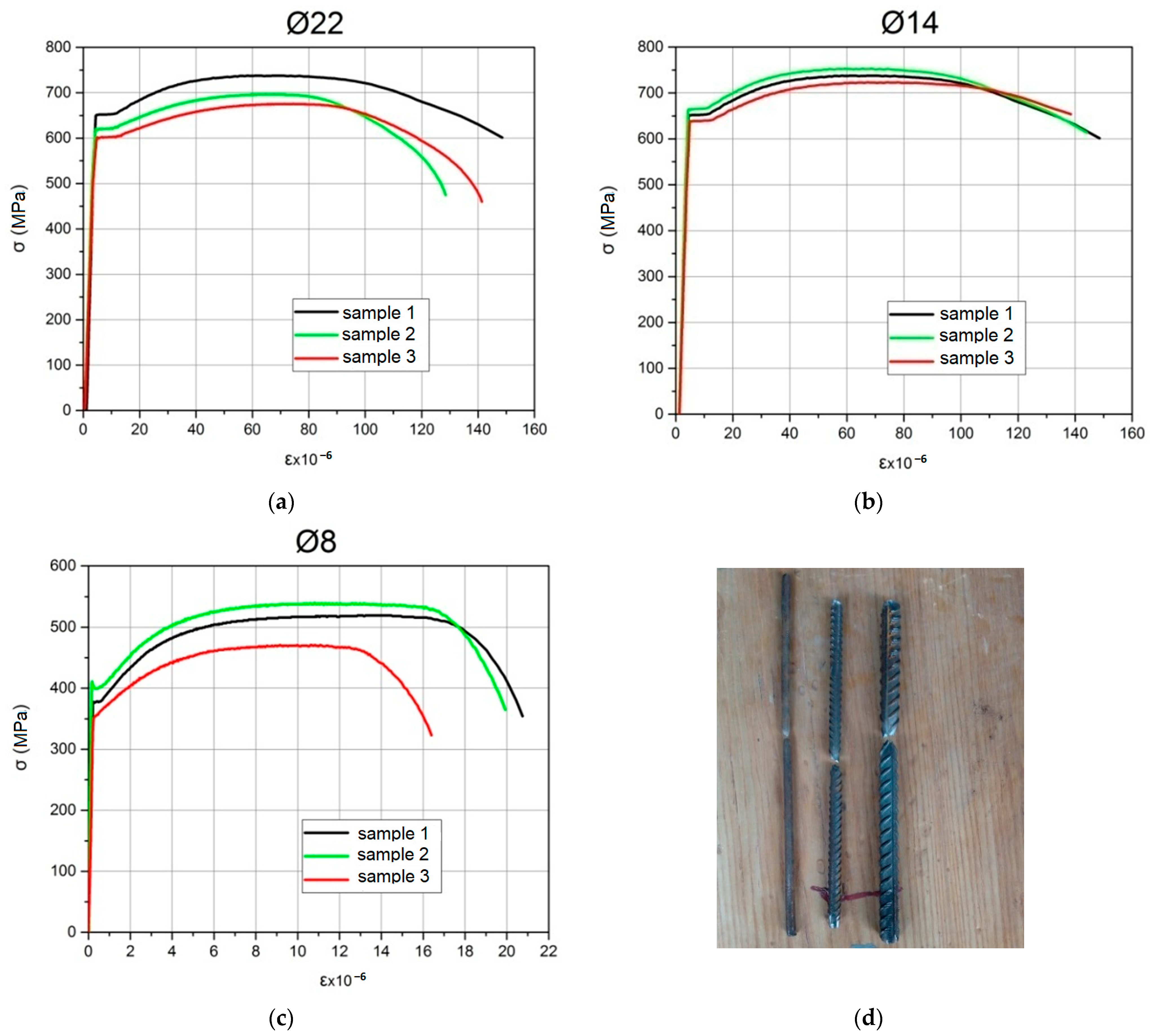









| Rebar | Number of Test Samples | Geometric Dimensions (mm): | fy MPa | fu, MPa | fyw, MPa | εs | εu | Es, GPa | Class |
|---|---|---|---|---|---|---|---|---|---|
| Smooth | 3 | Ø8, l = 400 mm | 376 | 301.4 | A240C | ||||
| Ribbed | 3 | Ø14, l = 400 mm | 636.9 | 722.8 | 0.00302 | 0.048 | 2.11 | A500C | |
| Ribbed | 3 | Ø22, l = 400 mm | 610.7 | 701.5 | 0.00291 | 0.070 | 2.10 | A500C |
| Sample | Number of Test Samples | Geometric Dimensions (mm): | fc,cube MPa | fc, MPa | fct MPa | fc,prism MPa | Ec, GPa | υ | Class |
|---|---|---|---|---|---|---|---|---|---|
| 1st Series: | |||||||||
| Cubes | 6 | 150 × 150 × 150 | 41.09 | - | - | - | - | - | C32/40 |
| Prisms | 4 | 150 × 150 × 600 | - | - | - | 30.46 | 31.35 | 0.12 | |
| Cylinders (for compression) | 4 | 100 × 200 | - | 30.49 | - | - | - | - | |
| Cylinders (for splitting) | 4 | 100 × 200 | - | - | 5.06 | - | - | - | |
| 2nd Series: | |||||||||
| Cubes | 6 | 150 × 150 × 150 | 45.91 | - | - | - | - | - | C32/40 |
| Prisms | 4 | 50 × 150 × 600 | - | - | - | 32.66 | 33.39 | 0.12 | |
| Cylinders (for compression) | 4 | 100 × 200 | - | 33.15 | - | - | - | - | |
| Cylinders (for splitting) | 4 | 100 × 200 | - | - | 6.13 | - | - | - | |
| Parameter | Value |
|---|---|
| Weight of the mesh, g/cm2 | 1.56 |
| Tensile strength, MPa | 5800 |
| Modulus of elasticity, GPa | 270 |
| Ultimate strain, % | 2.15 |
| Equivalent thickness of dry material in the longitudinal direction, mm | 0.0445 |
| Equivalent thickness of dry material in the transverse direction, mm | 0.0115 |
| Ultimate tensile strength in the longitudinal direction per unit width, kN/m | 264 |
| Ultimate tensile strength in the transverse direction per unit width, kN/m | 66.5 |
| Parameter | Value |
|---|---|
| Water consumption per 100 kg of solution, L | 24–26 |
| Consumption (dry product), kg/m2/mm | 1.210–1.230 |
| Compressive strength at the age of 28 days, MPa | 29 |
| Bending strength at the age of 28 days, MPa | 3.5 |
| Modulus of elasticity, GPa | 6 |
| Name of the Testing Beams | Name of the Testing Cross Section of the Beam | Type of the Researching |
|---|---|---|
| BO 2.1 | BO 2.1.1 | Non-strengthened with a/d = 2 (control sample) |
| BO 2.1.2 | ||
| BSC 2.1-0 | BSC 2.1.1-0 | Strengthened without initial loading by three stirrups of composite materials |
| BSC 2.1.2-0 | ||
| BSC 2.2-0.3 | BSC 2.2.1-0.3 | Strengthened at 30% load from bearing capacity of the control samples by three stirrups of composite materials |
| BSC 2.2.2-0.3 | ||
| BSC 2.3-0.5 | BSC 2.3.1-0.5 | Strengthened at 50% load from bearing capacity of the control samples by three stirrups of composite materials |
| BSC 2.3.2-0.5 | ||
| BSC 2.4-0.7 | BSC 2.4.1-0.7 | Strengthened at 70% load from bearing capacity of the control samples by three stirrups of composite materials |
| BSC 2.4.2-0.7 |
| Name of the Testing Beams | Name of the Testing Cross-Section of the Beam | Cross-Section bxh mm | Beam Span, l0 mm | Shear Span of the Section a/d | , kN | The Average Value of the Bearing Capacity, , kN | |
|---|---|---|---|---|---|---|---|
| BO 2.1 | BO 2.1.1 | 201 × 101 | 1900 | 2 | 150 | 148.5 | - |
| BO 2.1.2 | 147 | ||||||
| BSC 2.1-0 | BSC 2.1.1-0 | 199 × 100 | 187 | 185.5 | 1.25 | ||
| BSC 2.1.2-0 | 184 | ||||||
| BSC 2.2-0.3 | BSC 2.2.1-0.3 | 200 × 100 | 181 | 180 | 1.21 | ||
| BSC 2.2.2-0.3 | 179 | ||||||
| BSC 2.3-0.5 | BSC 2.3.1-0.5 | 201 × 98 | 176.5 | 178.25 | 1.20 | ||
| BSC 2.3.2-0.5 | 180 | ||||||
| BSC 2.4-0.7 | BSC 2.4.1-0.7 | 201 × 101 | 169 | 171 | 1.16 | ||
| BSC 2.4.2-0.7 | 173 |
| Name of the Testing Beams | Name of the Testing Cross-Section of the Beam | , kN | The Average Value of the Bearing Capacity, , kN | Increasing Strengthening Value, kN | |
|---|---|---|---|---|---|
| BO 2.1 | BO 2.1.1 | 150 | 148.5 | - | - |
| BO 2.1.2 | 147 | ||||
| BSC 2.1-0 | BSC 2.1.1-0 | 187 | 185.5 | 37 | 1 |
| BSC 2.1.2-0 | 184 | ||||
| BSC 2.2-0.3 | BSC 2.2.1-0.3 | 181 | 180 | 31.5 | 0.85 |
| BSC 2.2.2-0.3 | 179 | ||||
| BSC 2.3-0.5 | BSC 2.3.1-0.5 | 176.5 | 178.25 | 29.75 | 0.80 |
| BSC 2.3.2-0.5 | 180 | ||||
| BSC 2.4-0.7 | BSC 2.4.1-0.7 | 169 | 171 | 22.5 | 0.61 |
| BSC 2.4.2-0.7 | 173 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vegera, P.; Borzovic, V.; Blikharskyi, Z.; Grynyova, I.; Baran, J. Shear Strengthening with a Fiber-Reinforced Cementitious Matrix of Reinforced Concrete Elements Under Different Levels of Loads: An Experimental Investigation. Constr. Mater. 2024, 4, 721-737. https://doi.org/10.3390/constrmater4040039
Vegera P, Borzovic V, Blikharskyi Z, Grynyova I, Baran J. Shear Strengthening with a Fiber-Reinforced Cementitious Matrix of Reinforced Concrete Elements Under Different Levels of Loads: An Experimental Investigation. Construction Materials. 2024; 4(4):721-737. https://doi.org/10.3390/constrmater4040039
Chicago/Turabian StyleVegera, Pavlo, Viktor Borzovic, Zinovii Blikharskyi, Iryna Grynyova, and Jaroslav Baran. 2024. "Shear Strengthening with a Fiber-Reinforced Cementitious Matrix of Reinforced Concrete Elements Under Different Levels of Loads: An Experimental Investigation" Construction Materials 4, no. 4: 721-737. https://doi.org/10.3390/constrmater4040039
APA StyleVegera, P., Borzovic, V., Blikharskyi, Z., Grynyova, I., & Baran, J. (2024). Shear Strengthening with a Fiber-Reinforced Cementitious Matrix of Reinforced Concrete Elements Under Different Levels of Loads: An Experimental Investigation. Construction Materials, 4(4), 721-737. https://doi.org/10.3390/constrmater4040039





