The Behavior of Reinforced Concrete Slabs Strengthened by Different Patterns and Percentages of Carbon Fiber-Reinforced Polymer (CFRP) Plate
Abstract
:1. Introduction
2. Work Description
3. Finite Element Analysis
3.1. Modeling
3.2. Material Modelling
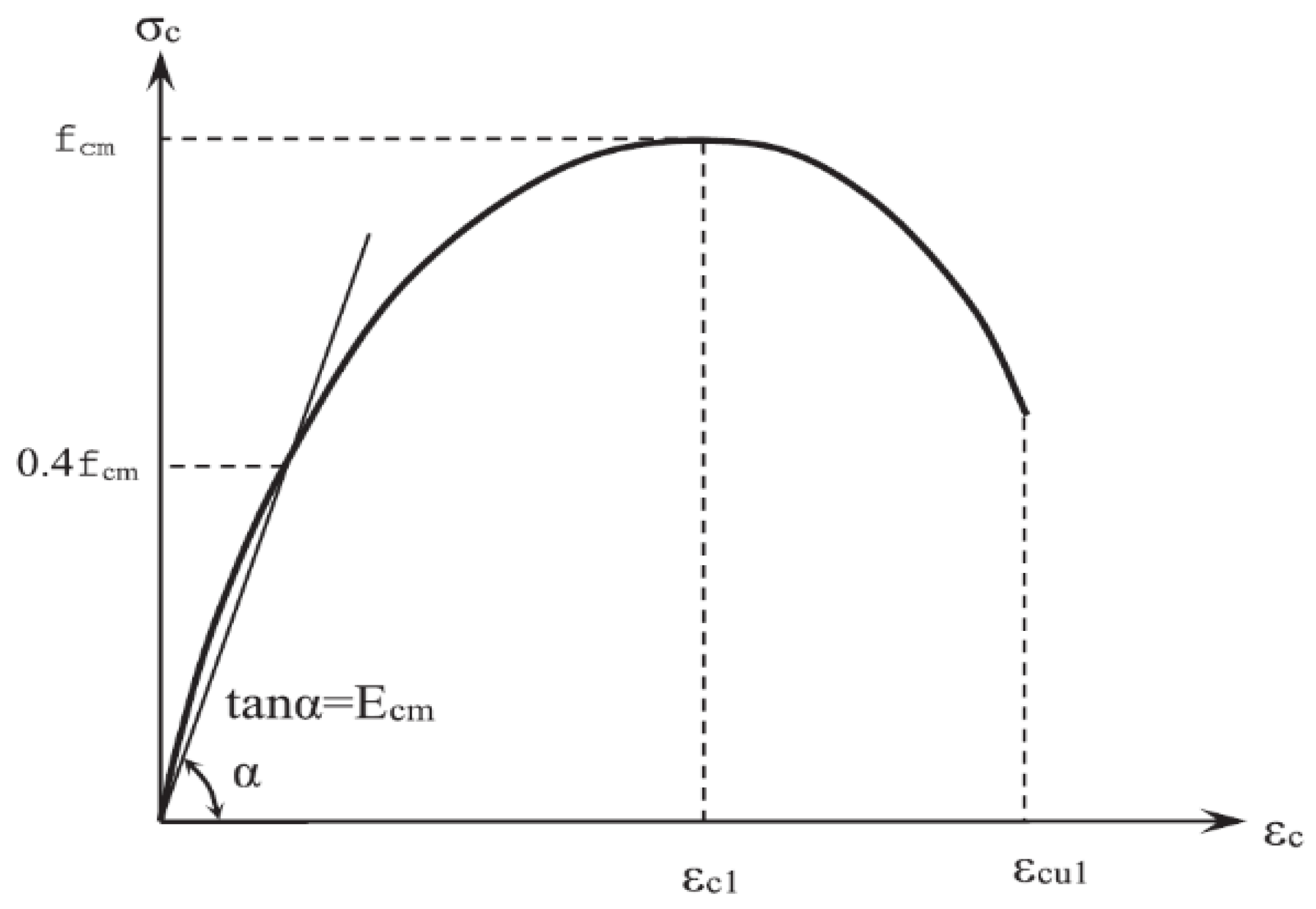
3.2.1. Concrete
3.2.2. Steel Reinforcement and FRP Sheets
3.2.3. Loading and Boundary Conditions
- To disperse the load over the supporting area and enable the slab corners to lift, the supports were designed as a rigid surface.
- Release constraints: This step was a consequence of the previous step.
- Loading: This was displacement-based until failure occurred, while the upper limit of the displacement values was chosen so that the entire load–deflection plateau, including the pre-and post-failure regions, could be captured.
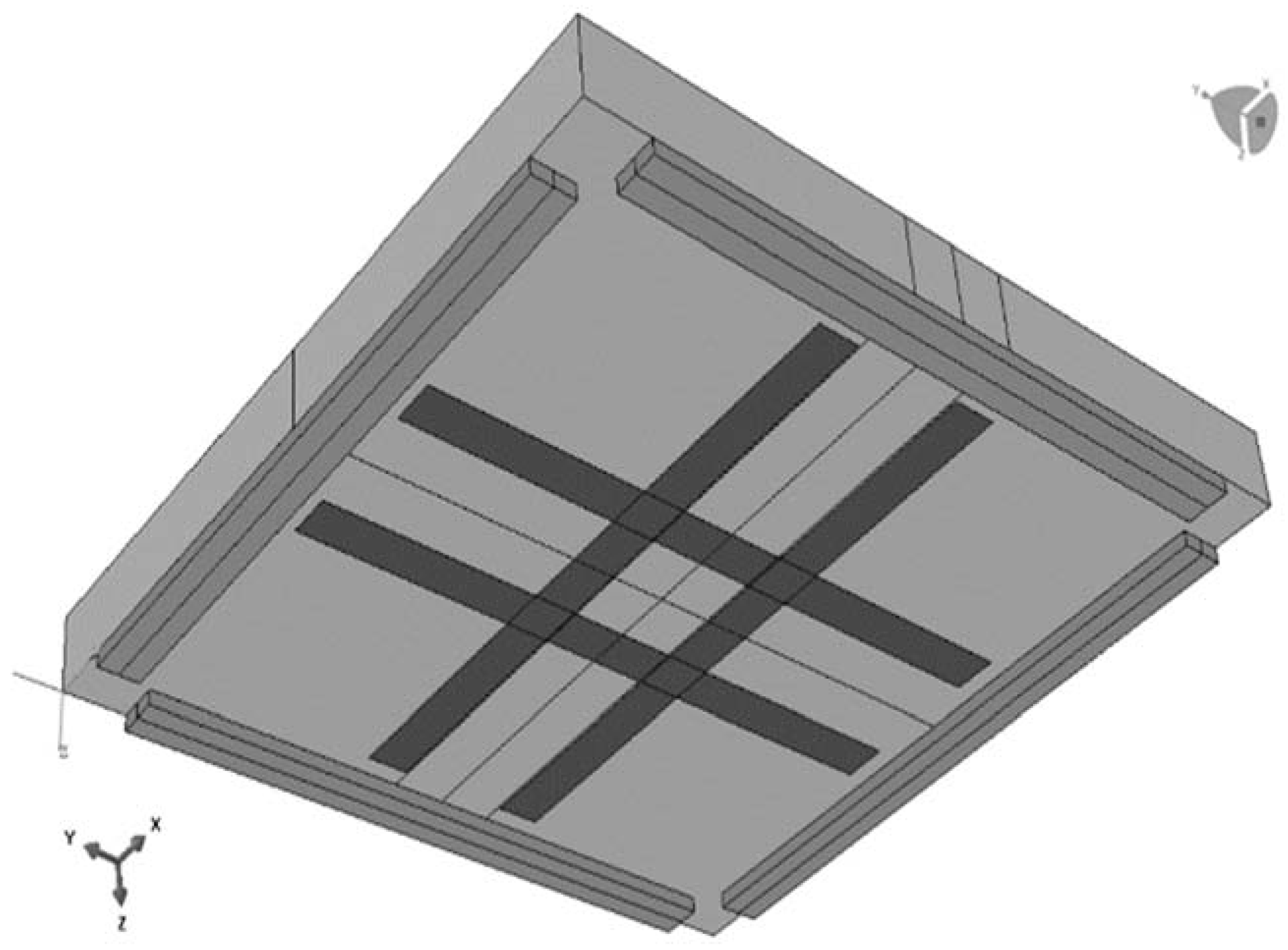
- As shown in Figure 1, the corners of the slab were free to raise, and the slab’s perimeter was only held horizontally. The slab perimeter was supported by a solid surface that extended 1600 mm into the slab. The stress state surrounding the column region could be effectively captured, thanks to this boundary condition representation.
4. Results and Discussions
5. Conclusions
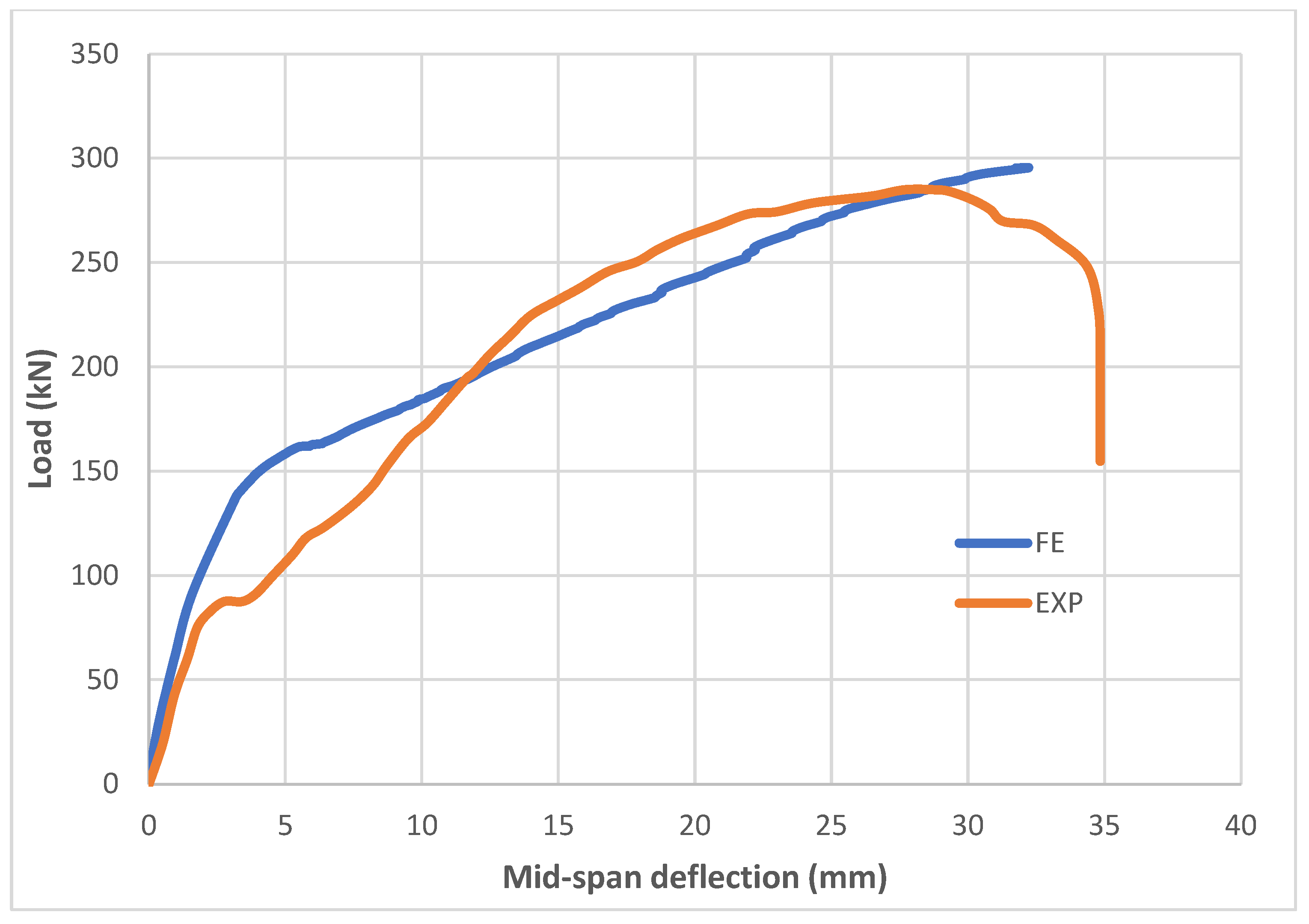
- The proposed numerical model showed good agreement with the experimental results, demonstrating that the use of CFRP significantly improved the load–deflection behavior by increasing the ultimate loads. The numerical simulation demonstrated a reliable prediction of crack patterns, with both the experimental and numerical results showing cracks concentrated in the middle region due to high tensile strains. The load–deflection relationships exhibited good agreement, though the experimental specimens were slightly stiffer.
- The maximum deflection and failure load were marginally higher in the experimental specimens (35 mm and 282 kN) compared with the numerical results (32 mm and 295 kN). Additionally, nonlinear behavior was initiated earlier in the experimental specimens (80 kN) than in the numerical ones (135 kN), suggesting the numerical model may overestimate stiffness during early loading stages. The numerical and experimental load–deflection relationships for the specimens with CFRP showed good agreement, with slight differences in their stiffness, deflection (22 mm vs. 23 mm), and failure load (427 kN vs. 402 kN).
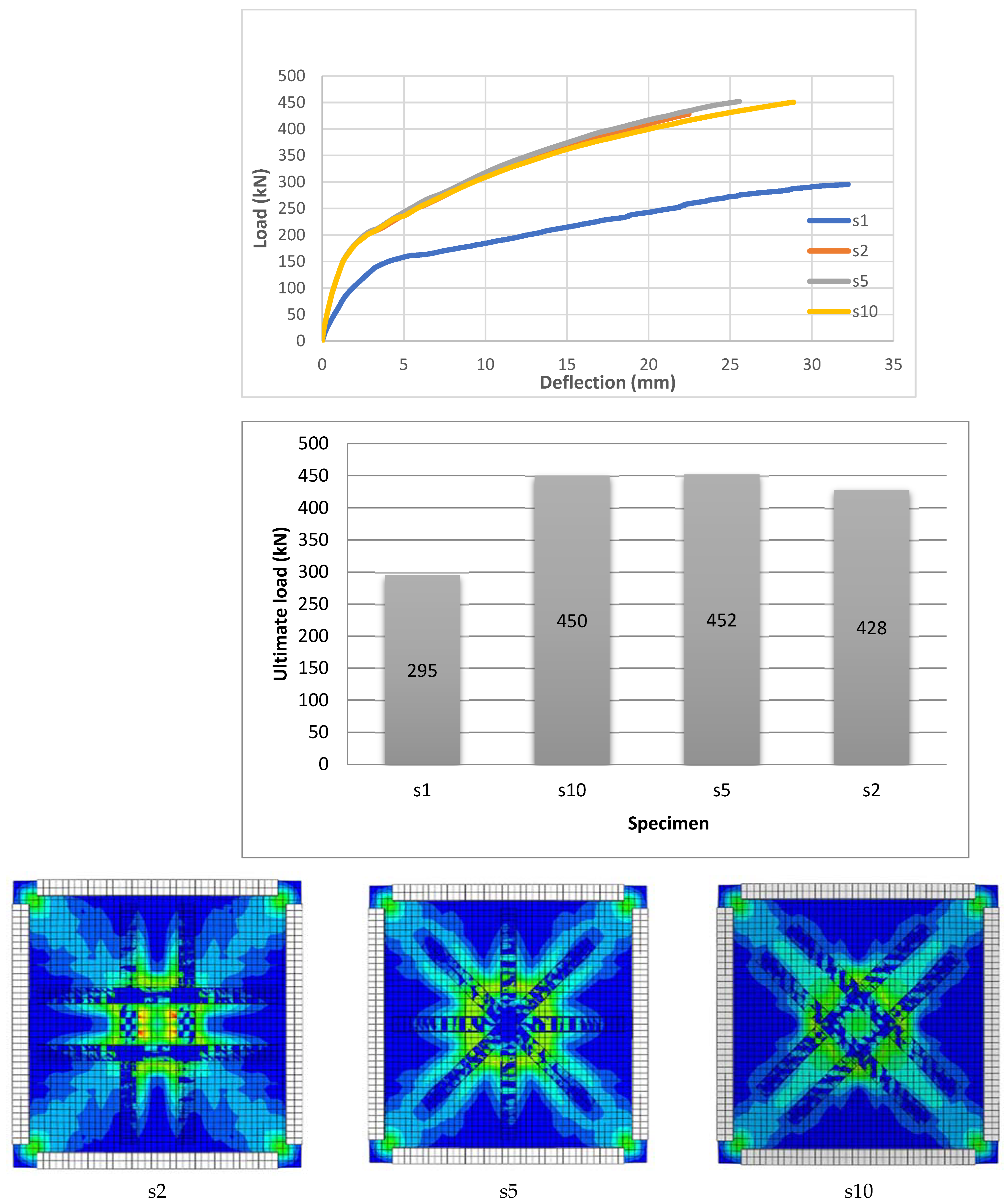
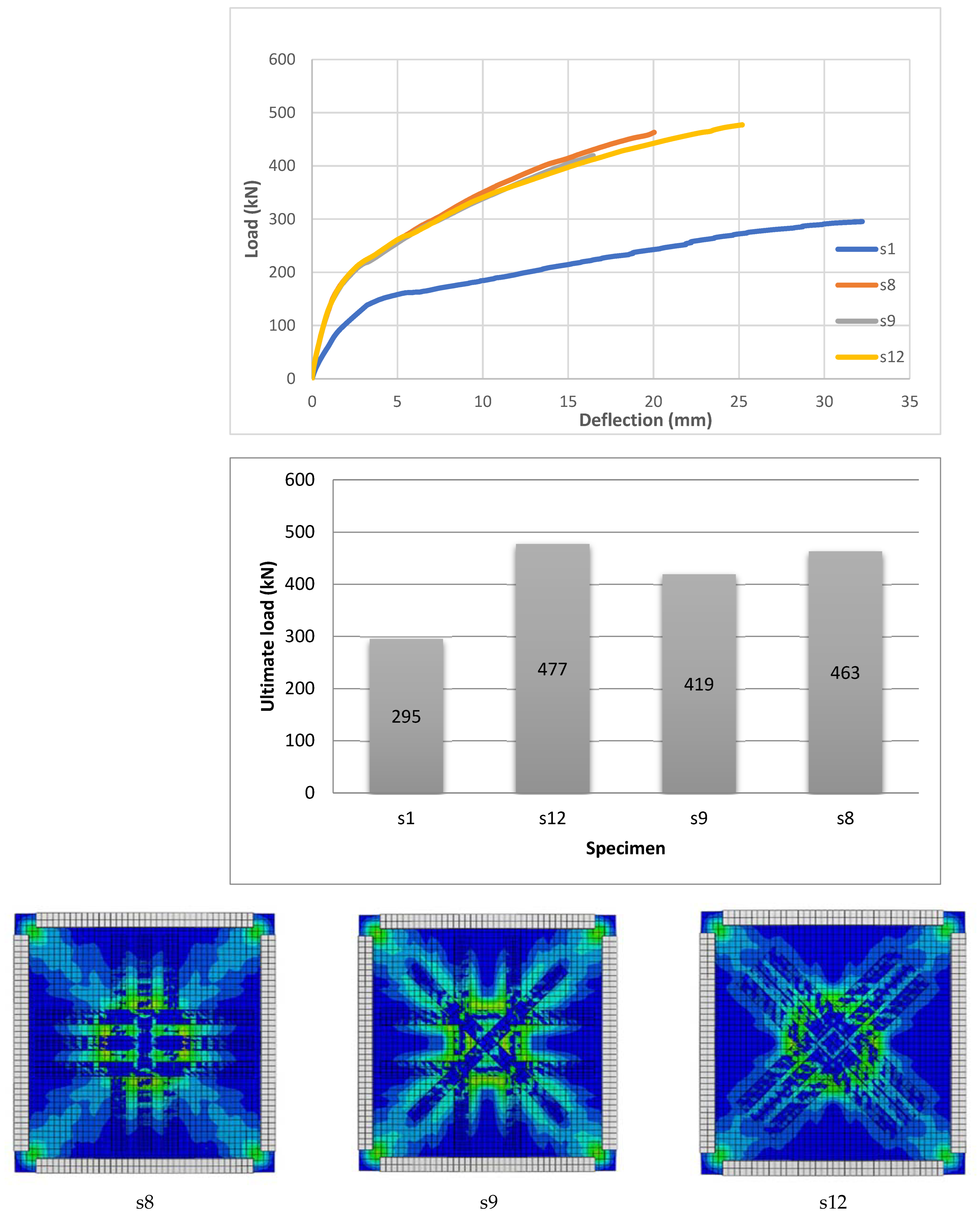
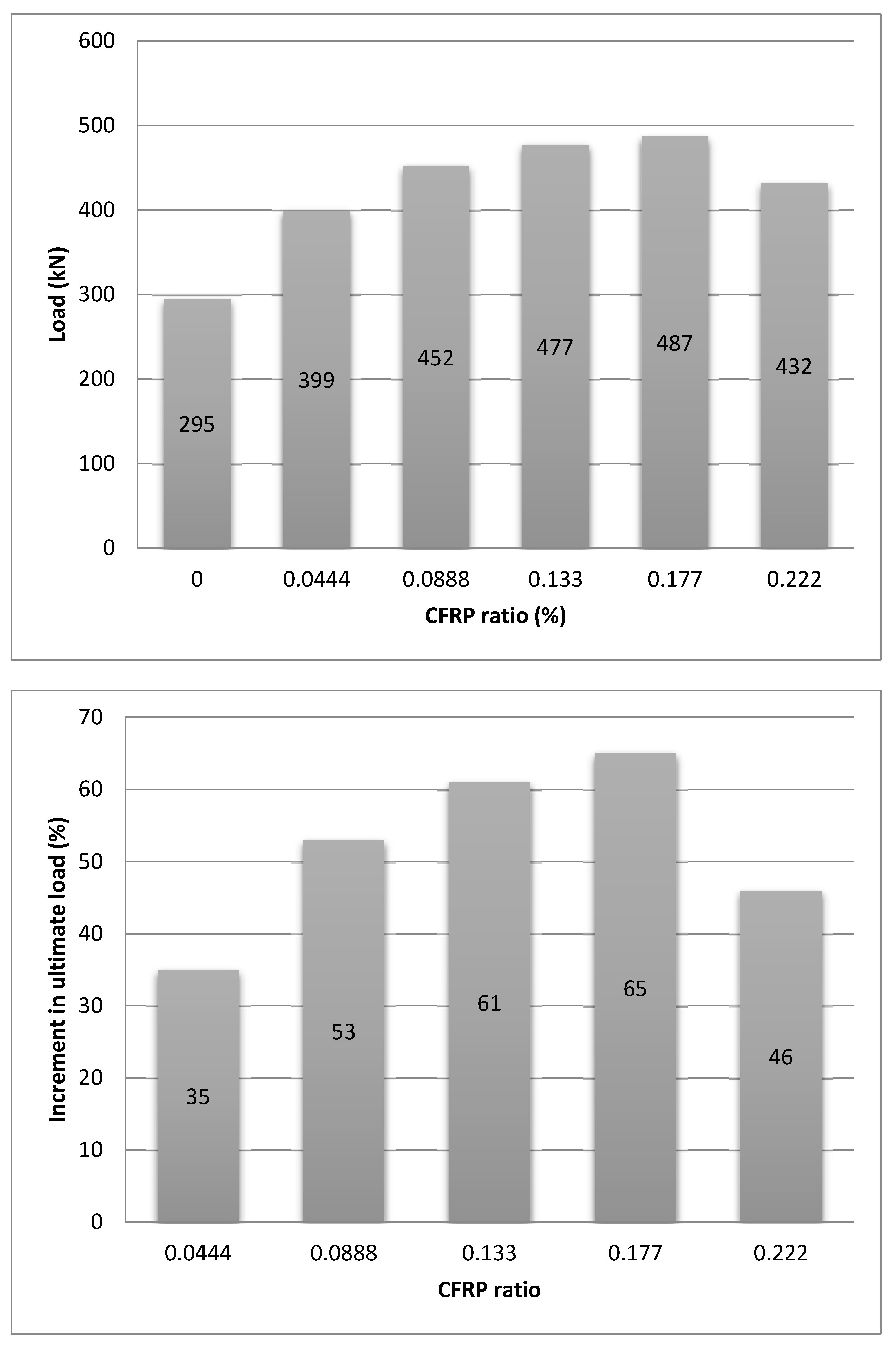
- The use of CFRP significantly improved the load–deflection behavior, increasing the ultimate loads by 35% (e.g., 452 kN for S5) compared with the specimen without CFRP (s1) while reducing the ultimate deflection at failure, with S5 achieving the highest deflection among the CFRP specimens. When compared with the other CFRP specimens at failure, S12 had the biggest ultimate load and a deflection that was more than 5 mm larger. Compared with the specimen without CFRP (s1), the addition of CFRP enhanced the load–deflection behavior and increased the ultimate loads (e.g., 477 kN for s12).
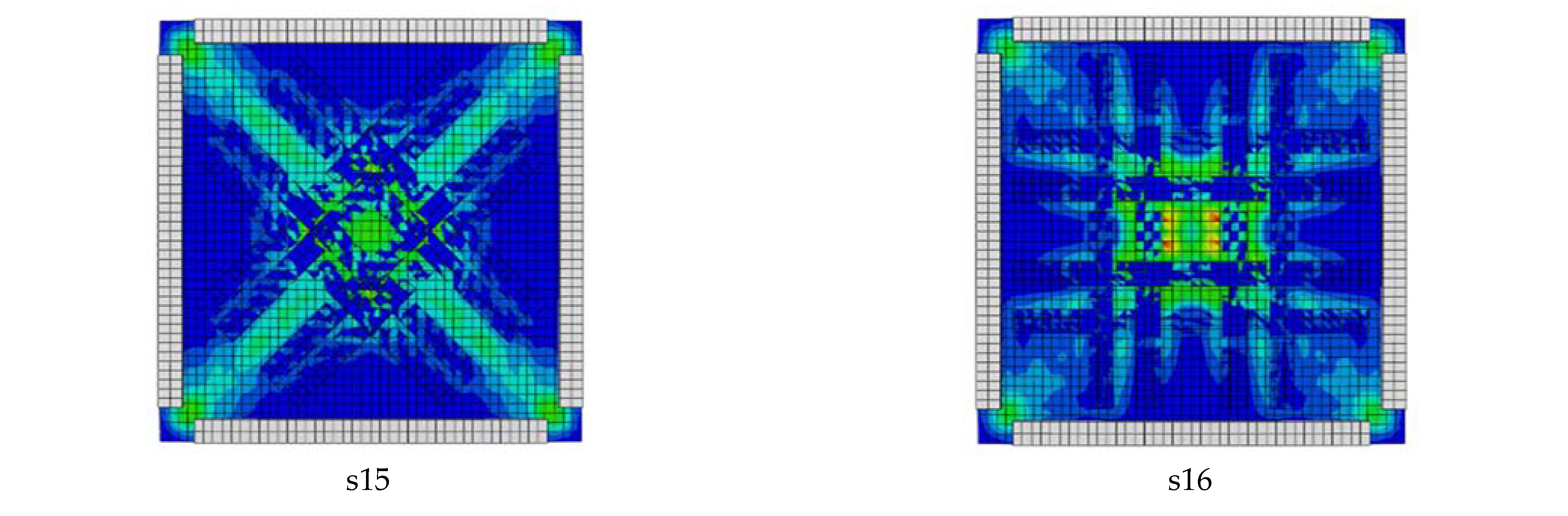
- All CFRP specimens showed comparable behavior up to 200 kN before diverging at larger loads, although specimen s11 achieved the maximum ultimate load (487 kN) and deflection, demonstrating the improved load–deflection behavior brought about by CFRP use. The CFRP application’s improved load–deflection behavior caused specimen s16’s ultimate load to increase to 432 kN. But at around 160 kN, nonlinear behavior started to show, and its ultimate deflection was 58% less than that of specimen s1. The use of CFRP increased the ultimate loads by up to 65%, with the highest load achieved at a CFRP ratio of 0.177, while ratios above 0.177 reduced the ultimate load.
- Optimizing CFRP strengthening configurations, considering factors like plate placement, orientation, and strengthening percentages based on load and slab specifications, along with following guidelines for surface preparation, bonding conditions, and curing times, will ensure effective application; furthermore, the selection of CFRP systems for retrofitting RC structures should consider cost, material compatibility, and environmental conditions, while addressing real-world challenges, such as handling large CFRP sheets and achieving uniform bonding on irregular surfaces.
6. Design Recommendations and Applications
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jones, A.E.K.; Morrison, J. Flat slab design: Past, present and future. Proc. Inst. Civ. Eng.-Struct. Build. 2005, 158, 133–140. [Google Scholar] [CrossRef]
- Sagban, S.A.A.; Abbas, M.; Hussain, H.K. A Review on Flat Slab Punching Shear Reinforcement. J. Univ. Babylon Eng. Sci. 2019, 27, 44–58. [Google Scholar]
- Lapi, M.; Ramos, A.P.; Orlando, M. Flat slab strengthening techniques against punching-shear. Eng. Struct. 2019, 180, 160–180. [Google Scholar] [CrossRef]
- Saleh, H.; Abdouka, K.; Al-Mahaidi, R.; Kalfat, R. Strengthening of slab–column connections against punching shear using FRP materials: State-of-the-art review. Aust. J. Struct. Eng. 2018, 19, 188–206. [Google Scholar] [CrossRef]
- Amiri, S.; Talaeitaba, S.B. Punching shear strengthening of flat slabs with EBROG and EBRIG—FRP strips. Structures 2020, 26, 139–155. [Google Scholar] [CrossRef]
- Inácio, M.M.G.; Ramos, A.P.; Faria, D.M.V. Strengthening of flat slabs with transverse reinforcement by introduction of steel bolts using different anchorage approaches. Eng. Struct. 2012, 44, 63–77. [Google Scholar] [CrossRef]
- Yaman, S.S.A.-K.; Abdulhameed, A.Y.; Mezgeen, S.A.; Ferhadi, R.; Mand, K.A. Predicting strength and strain of circular concrete cross-sections confined with FRP under axial compression by utilizing artificial neural networks. Comput. Concr. 2024, 34, 93–122. [Google Scholar]
- Mohamed, O.A.; Kewalramani, M.; Khattab, R. Fiber Reinforced Polymer Laminates for Strengthening of RC Slabs against Punching Shear: A Review. Polymers 2020, 12, 685. [Google Scholar] [CrossRef]
- Abdullah, A.M. Analysis of Repaired/Strengthened RC Structures Using Composite Materials: Punching Shear; The University of Manchester: Manchester, UK, 2011. [Google Scholar]
- Oehlers, D.J.; Liu, I.; Seracino, R. Shear deformation debonding of adhesively bonded plates. Proc. Inst. Civ. Eng.-Struct. Build. 2005, 158, 77–84. [Google Scholar] [CrossRef]
- Teng, J.; Chen, J. Debonding failures of RC beams strengthened with externally bonded FRP reinforcement: Behaviour and modelling. In Proceedings of the First Asia-Pacific Conference on FRP in Structures (APFIS 2007), The University of Hong Kong, Hong Kong, China, 12–14 December 2007; pp. 12–14. [Google Scholar]
- Shiyal, H.W.; Jawad, D.A. Strengthening of flat slab with openings under punching shear load. Univ. Thi-Qar J. Eng. Sci. 2022, 12, 174–183. [Google Scholar] [CrossRef]
- Ueda, T.; Dai, J. Interface bond between FRP sheets and concrete substrates: Properties, numerical modeling and roles in member behaviour. Prog. Struct. Eng. Mater. 2005, 7, 27–43. [Google Scholar] [CrossRef]
- Daneshvar, D.; Behnood, A.; Robisson, A. Interfacial bond in concrete-to-concrete composites: A review. Constr. Build. Mater. 2022, 359, 129195. [Google Scholar] [CrossRef]
- Abdullah, A.; Bailey, C.G. Punching behaviour of column-slab connection strengthened with non-prestressed or prestressed FRP plates. Eng. Struct. 2018, 160, 229–242. [Google Scholar] [CrossRef]
- Cheng, H.T.; Mohammed, B.S.; Mustapha, K.N. Finite element analysis and structural design of pretensioned inverted T-beams with web openings. Front. Archit. Civ. Eng. China 2009, 3, 148–157. [Google Scholar] [CrossRef]
- Alsaeq, H.M. Effects of opening shape and location on the structural strength of RC deep beams with openings. Int. J. Civ. Environ. Eng. 2013, 7, 494–499. [Google Scholar]
- Hassan, H.M.; Arab, M.A.E.S.; Ismail El-Kassas, A. Behavior of high strength self compacted concrete deep beams with web openings. Heliyon 2019, 5, e01524. [Google Scholar] [CrossRef]
- Ali, Y.A.; Assi, L.N.; Abas, H.; Taresh, H.R.; Dang, C.N.; Ghahari, S. Numerical Investigation on Effect of Opening Ratio on Structural Performance of Reinforced Concrete Deep Beam Reinforced with CFRP Enhancements. Infrastructures 2022, 8, 2. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, T.; Wang, X. Mesoscale modelling of concrete damage in FRP-concrete debonding failure. Eng. Struct. 2023, 289, 116310. [Google Scholar] [CrossRef]
- Lu, X.Z.; Teng, J.G.; Ye, L.P.; Jiang, J.J. Bond–slip models for FRP sheets/plates bonded to concrete. Eng. Struct. 2005, 27, 920–937. [Google Scholar] [CrossRef]
- Lu, X.Z.; Jiang, J.J.; Teng, J.G.; Ye, L.P. Finite element simulation of debonding in FRP-to-concrete bonded joints. Constr. Build. Mater. 2006, 20, 412–424. [Google Scholar] [CrossRef]
- Richard, C.E.; Eivind, H. Shearing Strength of Reinforced Concrete Slabs. ACI J. Proc. 1956, 53, 29–58. [Google Scholar]
- Amin, G. An Efficient Solution to Punching of Slabs. Concr. Int. 1989, 11, 50–54. [Google Scholar]
- Ebead, U.; Marzouk, H. Strengthening of Two-Way Slabs Using Steel Plates. ACI Struct. J. 2002, 99, 23–31. [Google Scholar]
- El-Salakawy, M.A.P.E.F.; Khaled, A.S. New Shear Strengthening Technique for Concrete Slab-Column Connections. ACI Struct. J. 2003, 100, 297–304. [Google Scholar]
- Kyriakos, S.; Shamim, A.S. Strengthening Concrete Slabs for Punching Shear with Carbon Fiber-Reinforced Polymer Laminates. ACI Struct. J. 2007, 104, 49. [Google Scholar]
- Binici, B.; Bayrak, O. Punching Shear Strengthening of Reinforced Concrete Flat Plates Using Carbon Fiber Reinforced Polymers. J. Struct. Eng. 2003, 129, 1173–1182. [Google Scholar] [CrossRef]
- Baris, B.; Oguzhan, B. Use of Fiber-Reinforced Polymers in Slab-Column Connection Upgrades. ACI Struct. J. 2005, 102, 93. [Google Scholar]
- Erki, M.A.; Heffernan, P.J. Reinforced concrete slabs externally strengthened with fibre-reinforced plastic materials. In Proceedings of the 2nd Symposium on Non-Metalic FRP Reinforcement for Concrete Structures (FRPRCS-2), Ghent, Belgium, 23–25 August 1995. [Google Scholar]
- Harajli, M.H.; Soudki, K.A. Shear Strengthening of Interior Slab–Column Connections Using Carbon Fiber-Reinforced Polymer Sheets. J. Compos. Constr. 2003, 7, 145–153. [Google Scholar] [CrossRef]
- Sharaf, M.H.; Soudki, K.A.; Dusen, M.V. CFRP Strengthening for Punching Shear of Interior Slab–Column Connections. J. Compos. Constr. 2006, 10, 410–418. [Google Scholar] [CrossRef]
- Kalfat, R.; Al-Mahaidi, R. Numerical and Experimental Validation of FRP Patch Anchors Used to Improve the Performance of FRP Laminates Bonded to Concrete. J. Compos. Constr. 2014, 18, A4013008. [Google Scholar] [CrossRef]
- El-Maaddawy, T.A.; Sherif, E.-S.I. Response of Concrete Corbels Reinforced with Internal Steel Rebars and External Composite Sheets: Experimental Testing and Finite Element Modeling. J. Compos. Constr. 2014, 18, 04013020. [Google Scholar] [CrossRef]
- Gouda, A.; El-Salakawy, E. Punching Shear Strength of GFRP-RC Interior Slab–Column Connections Subjected to Moment Transfer. J. Compos. Constr. 2016, 20, 04015037. [Google Scholar] [CrossRef]
- Salama, A.E.; Hassan, M.; Benmokrane, B. Effect of GFRP Shear Stirrups on Strength of Two-Way GFRP RC Edge Slabs: Experimental and Finite-Element Investigations. J. Struct. Eng. 2020, 146, 04020056. [Google Scholar] [CrossRef]
- El-Gendy, M.G.; El-Salakawy, E.F. Finite-Element Analysis of FRP-Reinforced Concrete Slab–Column Edge Connections Subjected to Reversed-Cyclic Lateral Loads. J. Compos. Constr. 2021, 25, 04020082. [Google Scholar] [CrossRef]
- Ali, Y.A.; Falah, M.W.; Naser, M.H. Finite Element Analysis of Beams Strengthened in Flexure with Carbon Fiber Reinforced Polymer Plates. AIP Conf. Proc. 2023, 2787, 080029. [Google Scholar] [CrossRef]
- Ali, Y.A.; Falah, M.W.; Ali, A.H.; Al-Mulali, M.Z.; AL-Khafaji, Z.S.; Hashim, T.M.; Sa’adi, A.H.M.A.; Al-Hashimi, O. Studying the Effect of Shear Stud Distribution on the Behavior of Steel–Reactive Powder Concrete Composite Beams Using ABAQUS Software. J. Mech. Behav. Mater. 2022, 31, 416–425. [Google Scholar] [CrossRef]
- ASTM D3039/D3039M; Standard Test Method for Tensile Properties of Polymer Matrix Composites Materials. Annual Book of ASTM Standards: West Conshohocken, PA, USA, 2008.
- Hibbitt, K.; Sorensen, I. ABAQUS Theory Manual, User Manual and Example Manual, version 6.7; Simulia: Providence, RI, USA, 2000. [Google Scholar]
- Lee, J.; Fenves, G.L. A return-mapping algorithm for plastic-damage models: 3-D and plane stress formulation. Int. J. Numer. Methods Eng. 2001, 50, 487–506. [Google Scholar] [CrossRef]
- Lubliner, J.; Oliver, J.; Oller, S.; Onate, E. A plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Eurocode 2. Eurocode 2: Design of concrete structures-part 1–1: General rules and rules for buildings, British Standard Institution. London 2005, 668, 659–668. [Google Scholar]
- Hafezolghorani, M.; Hejazi, F.; Vaghei, R.; Jaafar, M.S.B.; Karimzade, K. Simplified Damage Plasticity Model for Concrete. Struct. Eng. Int. 2017, 27, 68–78. [Google Scholar] [CrossRef]
- Kollar, L.P. Mechanics of Composite Structures; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Aminpour, N.; Memari, A. Numerical and experimental study on reinforced 3DCP walls filled with light-weight concrete. J. Build. Eng. 2024, 97, 110995. [Google Scholar] [CrossRef]
- Kareem, R.S.; Assi, L.N.; Alsalman, A.; Al-Manea, A. Effect of supplementary cementitious materials on RC concrete piles. In AIP Conference Proceedings; October AIP Publishing: Long Island, NY, USA, 2021; Volume 2404. [Google Scholar]
- Assi, L.N.; Alsalman, A.; Al-Hamadani, Y.A.; Kareem, R.; Khuzaie, H.M.A.A. September. Observations of Supplementary Cementitious Materials Effects on The Performance of Concrete Foundation. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Long Island, NY, USA, 2021; Volume 856, p. 012020. [Google Scholar]
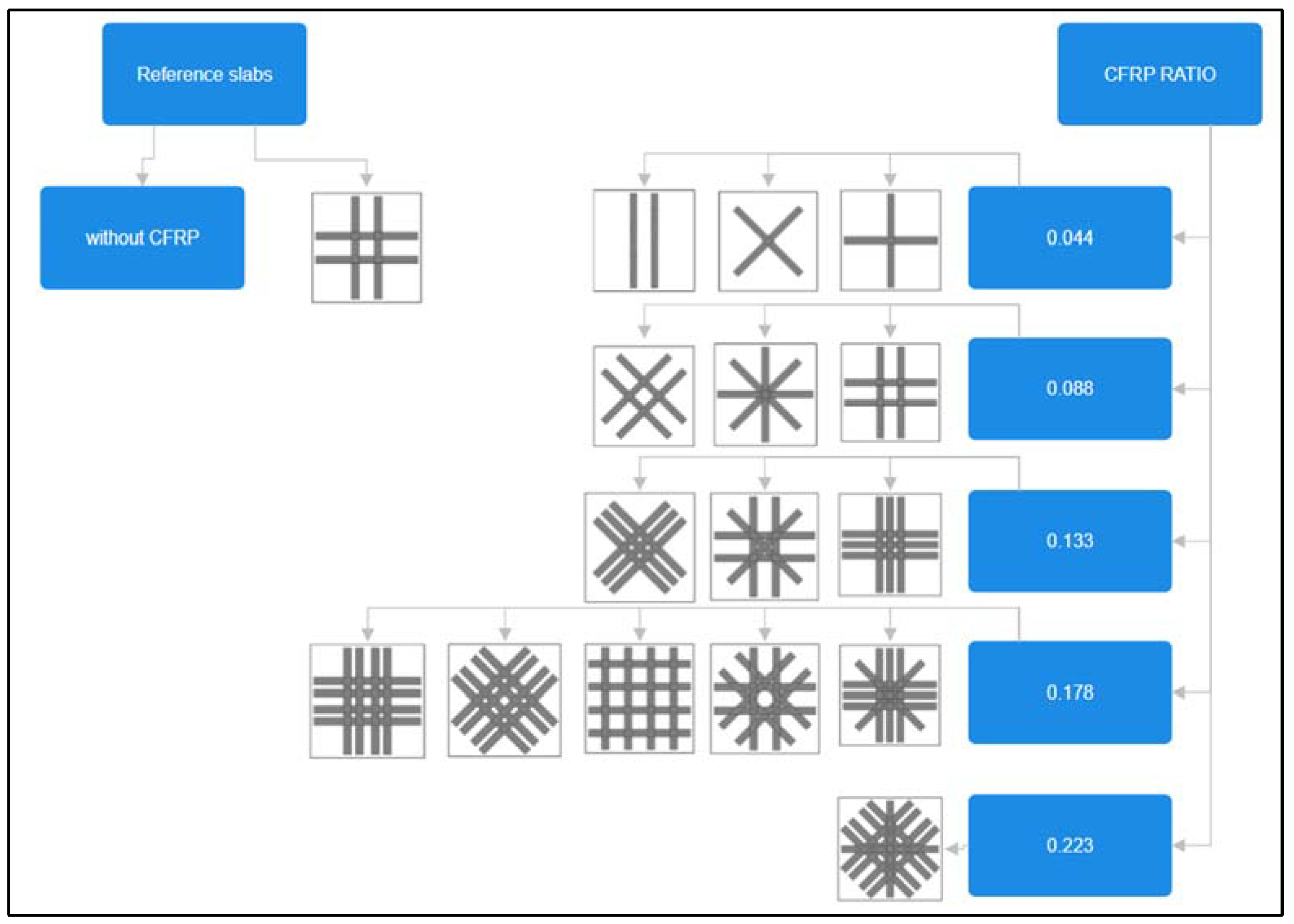











| Group No. | Specimen Code | CFRP Ratio | FRP Configuration | No. of CFRP Plates | Notes |
|---|---|---|---|---|---|
| Abdullah [9] | RS0 | Reference slab | - | 4 | Figure 1 |
| RS-F0 | CFRP | Cross | |||
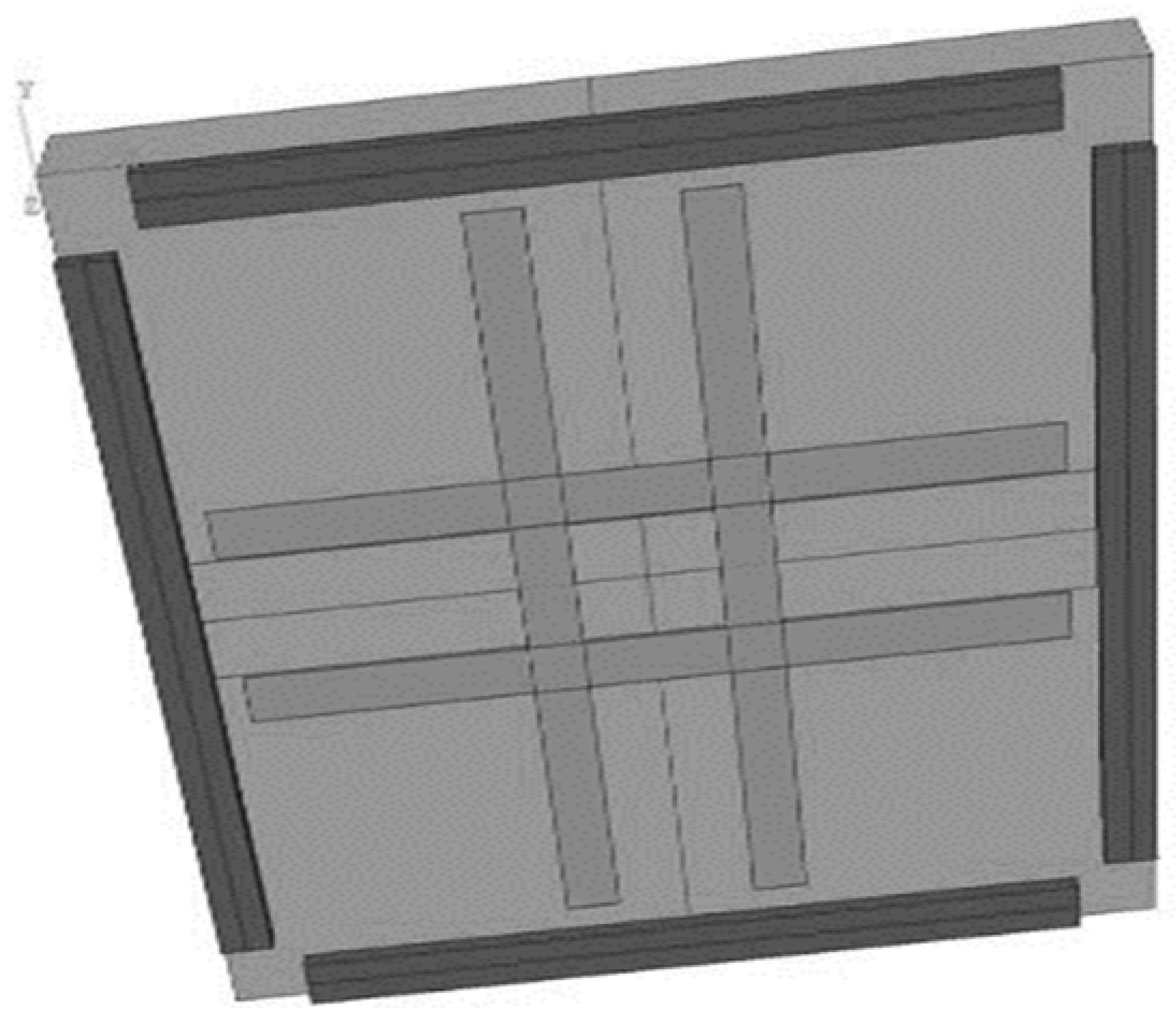
| 1 | s3 | 0.044 | Cross | 2 | Figure 3 |
| s4 | Augmentation | ||||
| s6 | Longitudinal | ||||
| 2 | s2 | 0.088 | Cross | 4 | Figure 4 |
| s5 | Cross-hatched | ||||
| s10 | Cross-diagonal | ||||
| 3 | s8 | 0.133 | Cross | 6 | Figure 5 |
| s9 | Cross-hatched | ||||
| s12 | Cross-diagonal | ||||
| 4 | s7 | 0.178 | Cross-hatched | 8 | Figure 6 |
| s11 | Cross-hatched | ||||
| s13 | Grid patterns | ||||
| s14 | Cross-diagonal | ||||
| s15 | Cross | ||||
| 5 | s16 | 0.223 | Cross-diagonal | 10 | Figure 7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Yousuf, A.; Al-Kamaki, Y.S.S.; Lateef, H.A.; Ali, Y.A.; Assi, L.N.; Kareem, R.S.; Dekhn, H.C. The Behavior of Reinforced Concrete Slabs Strengthened by Different Patterns and Percentages of Carbon Fiber-Reinforced Polymer (CFRP) Plate. Constr. Mater. 2025, 5, 24. https://doi.org/10.3390/constrmater5020024
Al-Yousuf A, Al-Kamaki YSS, Lateef HA, Ali YA, Assi LN, Kareem RS, Dekhn HC. The Behavior of Reinforced Concrete Slabs Strengthened by Different Patterns and Percentages of Carbon Fiber-Reinforced Polymer (CFRP) Plate. Construction Materials. 2025; 5(2):24. https://doi.org/10.3390/constrmater5020024
Chicago/Turabian StyleAl-Yousuf, Ayad, Yaman Sami Shareef Al-Kamaki, Hanadi Abdulridha Lateef, Yasar Ameer Ali, Lateef N. Assi, Rahman S. Kareem, and Hadeel Challoob Dekhn. 2025. "The Behavior of Reinforced Concrete Slabs Strengthened by Different Patterns and Percentages of Carbon Fiber-Reinforced Polymer (CFRP) Plate" Construction Materials 5, no. 2: 24. https://doi.org/10.3390/constrmater5020024
APA StyleAl-Yousuf, A., Al-Kamaki, Y. S. S., Lateef, H. A., Ali, Y. A., Assi, L. N., Kareem, R. S., & Dekhn, H. C. (2025). The Behavior of Reinforced Concrete Slabs Strengthened by Different Patterns and Percentages of Carbon Fiber-Reinforced Polymer (CFRP) Plate. Construction Materials, 5(2), 24. https://doi.org/10.3390/constrmater5020024







