Isotope and Spin Effects Induced by Compression of Paramagnetic Molecules
Abstract
1. Introduction
2. Calculation Procedure
3. Results and Discussion
3.1. Theory
3.2. Zero-Point Energies
3.3. Isotope Effects
3.4. Singlet-Triplet Splitting
3.5. Spin Densities
3.6. Applicability to Enzymes
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Buchachenko, A.L. Compressed atoms. J. Phys. Chem. B 2001, 105, 5839–5846. [Google Scholar] [CrossRef]
- Foresman, J.B.; Frish, E. Exploring Chemistry with Electronic Structure Methods, 2nd ed.; Gaussian, Inc.: Pittsburgh, PA, USA, 1996; p. 302. [Google Scholar]
- Zhao, Y.; Truhlar, D.G. Design of Density Functionals That Are Broadly Accurate for Thermochemistry, Thermochemical Kinetics, and Nonbonded Interactions. J. Phys. Chem. A 2005, 109, 5656–5667. [Google Scholar] [CrossRef] [PubMed]
- Kevin, E.R.; Pitonak, M.; Jurecka, P.; Hobza, P. Stabilization and Structure Calculations for Noncovalent Interactions in Extended Molecular Systems Based on Wave Function and Density Functional Theories. Chem. Rev. 2010, 110, 5023–5063. [Google Scholar]
- Ceponkus, J.; Uvdal, P.; Nelander, B. Intermolecular vibrations of different isotopologs of the water dimer: Experiments and density functional theory calculations. J. Chem. Phys. 2008, 129, 194306. [Google Scholar] [CrossRef] [PubMed]
- Verma, P.; Truhlar, D. Status and Challenges of Density Functional Theory. Trends Chem. 2020, 2, 302–318. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. GAUSSIAN 09; Gaussian Inc.: Pittsburgh, PA, USA, 2009. [Google Scholar]
- Korona, T.; Hesselmann, A.; Dodziuk, H. Symmetry-Adapted Perturbation Theory Applied to Endohedral Fullerene Complexes: A Stability Study of H2@C60 and 2H2@C60. J. Chem. Theory Comput. 2009, 5, 1585–1596. [Google Scholar] [CrossRef] [PubMed]
- Neese, F.; Wennmohs, F.; Becker, U.; Riplinger, C. The ORCA quantum chemistry program package. J. Chem. Phys. 2020, 152, 224108. [Google Scholar] [CrossRef] [PubMed]
- Barone, V.; Cimino, P.; Stendardo, E. Development and Validation of the B3LYP/N07D Computational Model for Structural Parameter and Magnetic Tensors of Large Free Radicals. J. Chem. Theory Comput. 2008, 4, 751–764. [Google Scholar] [CrossRef]
- Buchachenko, A.L. Compressed molecules and enzymes. Russ. J. Phys. Chem. B 2022, 16, 9–17. [Google Scholar] [CrossRef]
- Radford, H.E. Microwave Zeeman Effect of the hydroxyl radicals. Phys. Rev. 1961, 122, 345–358. [Google Scholar] [CrossRef]
- McConnell, H. Indirect hyperfine interactions in the paramagnetic resonance spectra of aromatic free radicals. J. Chem. Phys. 1956, 24, 764–769. [Google Scholar] [CrossRef]
- Mehta, A.D.; Rief, M.; Spudich, J.A.; Smith, D.A.; Simmons, R.M. Single-Molecule Biomechanics with Optical Methods. Science 1999, 283, 1689–1695. [Google Scholar] [CrossRef]
- Wang, M.D.; Schnitzer, M.J.; Yin, H.; Landick, R.; Gelles, J.; Block, S.M. Force and Velocity Measured for Single Molecules of RNA Polymerase. Science 1998, 282, 902–907. [Google Scholar] [CrossRef]
- Tskhovrebova, L.; Trinick, J.; Sleep, J.; Simmons, R. Elasticity and unfolding of single molecules of the giant muscle protein titin. Nature 1997, 387, 308–312. [Google Scholar] [CrossRef]
- Service, R.F. Watching DNA at Work. Science 1999, 283, 1668–1669. [Google Scholar] [CrossRef]
- Northrop, D.B. Unusual origins of isotope effects in enzyme-catalysed reactions. Philos. Trans. Royal Soc. B 2006, 361, 1341–1349. [Google Scholar] [CrossRef][Green Version]
- Park, H.; Girdaukas, G.G.; Northrop, D.B. Effect of pressure on heavy-atom isotope effect of yeast alcohol dehydrogenase. J. Am. Chem. Soc. 2006, 128, 1868–1872. [Google Scholar] [CrossRef]
- Klinman, J.P. An integrated model for enzyme catalysis emerges from studies of hydrogen tunneling. Chem. Phys. Lett. 2009, 471, 179–193. [Google Scholar] [CrossRef]
- Layfield, J.P.; Hammes-Schiffer, S. Hydrogen Tunneling in Enzymes and Biomimetic Models. Chem. Rev. 2014, 114, 3466–3494. [Google Scholar] [CrossRef]
- Li, P.; Soudackov, A.V.; Hammes-Schiffer, S. Fundamental Insights into Proton-Coupled Electron Transfer in Soybean Lipoxygenase from Quantum Mechanical/Molecular Mechanical Free Energy Simulations. J. Am. Chem. Soc. 2018, 140, 3068–3076. [Google Scholar] [CrossRef]
- Hu, S.; Soudackov, A.V.; Hammes-Schiffer, S.; Klinman, J.P. Enhanced Rigidification within a Double Mutant of Soybean Lipoxygenase Provides Experimental Support for Vibronically Nonadiabatic Proton-Coupled Electron Transfer Models. ACS Catal. 2017, 7, 3569–3574. [Google Scholar] [CrossRef]
- Luxem, K.E.; Leavitt, W.D.; Zhang, X. Large hydrogen isotope fractionation distinguishes nitrogenase-derived methane from other methane sources. Appl. Environ. Microbiol. 2020, 86, e00849-20. [Google Scholar] [CrossRef]
- Cavalli, A.; De Vivo, M.; Recanatini, M. Density functional study of the enzymatic reaction catalyzed by cyclin-dependent kinase. Chem. Commun. 2003, 11, 1308–1309. [Google Scholar] [CrossRef]
- Akola, J.; Jones, R.O. ATP hydrolysis in water—A density functional study. J. Phys. Chem. B 2003, 107, 11774–11783. [Google Scholar] [CrossRef]
- Buchachenko, A.L.; Kuznetsov, D.A.; Arkhangelsky, S.E.; Orlova, M.A. Spin Biochemistry: Magnetic 24Mg-25Mg-26Mg isotope effect in enzymatic phosphorylation. Cell 2005, 43, 243–252. [Google Scholar]
- Buchachenko, A.L.; Lukzen, N.N.; Pedersen, J.B. On the magnetic field and isotope effects in enzymatic phosphorylation. Chem. Phys. Lett. 2006, 434, 139–143. [Google Scholar] [CrossRef]
- Buchachenko, A.L.; Kuznetsov, D.A.; Breslavskaya, N.N. Chemistry of enzymatic ATP synthesis: An insight through the isotope window. Chem. Rev. 2012, 112, 2042–2058. [Google Scholar] [CrossRef]
- Buchachenko, A.L.; Orlov, A.P.; Kuznetsov, D.A.; Breslavskaya, N.N. Magnetic isotope and magnetic field effects on the DNA synthesis. Nucleic Acids Res. 2013, 41, 8300–8308. [Google Scholar] [CrossRef]
- Buchachenko, A.L.; Orlov, A.P.; Kuznetsov, D.A.; Breslavskaya, N.N. Magnetic control of the DNA synthesis. Chem. Phys. Lett. 2013, 586, 138–142. [Google Scholar] [CrossRef]
- Buchachenko, A.L.; Lawler, R.G. New possibilities for magnetic control of chemical and biochemical reactions. Acc. Chem. Res. 2017, 50, 877–884. [Google Scholar] [CrossRef]
- Buchachenko, A.L.; Bukhvostov, A.; Ermakov, K.; Kuznetsov, D.A. Nuclear spin selectivity in enzymatic catalysis. Arch. Biochem. Biophys. 2019, 667, 30–35. [Google Scholar] [CrossRef]
- Lahiri, S.D.; Wang, P.-F.; Babbitt, P.C.; McLeish, M.J.; Kenyon, G.L.; Allen, K.N. A structure of Torpedo californica creatine kinase. Biochemistry 2001, 41, 13861–13872. [Google Scholar] [CrossRef]
- Wyss, M.; James, P.; Schlegel, T.; Wallimann, T. Limited proteolysis of creatine kinase. Implications for three-dimensional structure and for conformational substates. Biochemistry 1993, 32, 10727–10735. [Google Scholar] [CrossRef]
- Buchachenko, A.L.; Kuznetsov, D.A.; Breslavskaya, N.N. Radical mechanism of enzymatic ATP synthesis: DFT calculations and experimental control. J. Phys. Chem. B 2010, 32, 2287–2292. [Google Scholar] [CrossRef]
- Buchachenko, A.L.; Kouznetsov, D.A. Magnetic control of enzymatic phosphorylation. J. Phys. Chem. Biophys. 2014, 4, 142–151. [Google Scholar] [CrossRef]
- Kuznetsov, D.A.; Buchachenko, A.L. Nuclear magnetic ions of magnesium, calcium, and zinc as a powerful and universal means for killing cancer cells. Russ. J. Phys. Chem. B 2018, 12, 690–694. [Google Scholar] [CrossRef]
- Buchachenko, A.L.; Bukhvostov, A.A.; Ermakov, K.V.; Kuznetsov, D.A. A specific role of magnetic isotopes in biological and ecological systems. Progr. Biophys. Mol. Biol. 2020, 155, 1–19. [Google Scholar] [CrossRef]
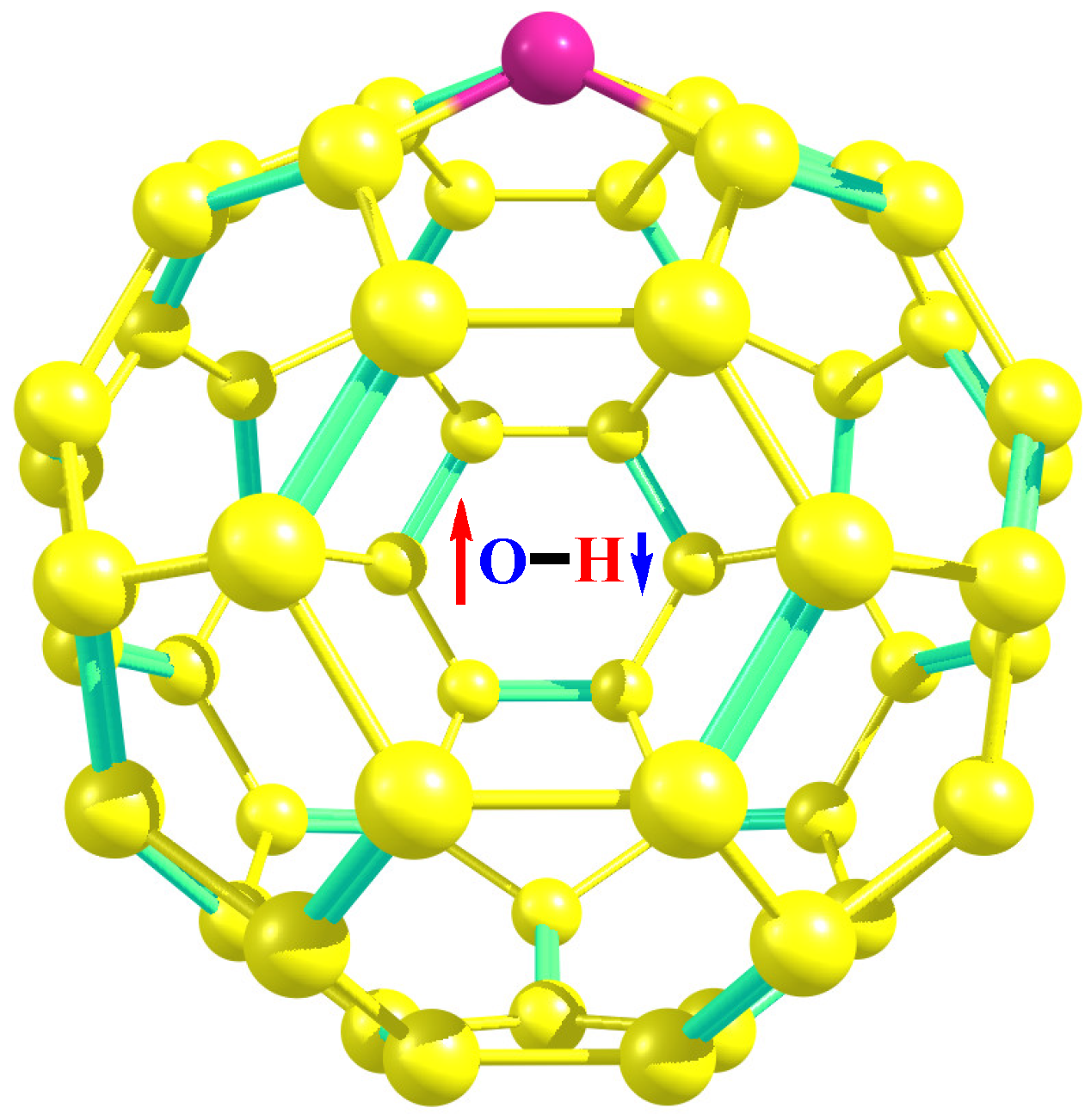
| Molecules | ZPE, kcal/mol | ||
|---|---|---|---|
| Free | Compressed in S State | Compressed in T State | |
| H2+ | 2.63 | 11.22 | 8.03 |
| D2+ | 1.86 | 8.45 | 5.24 |
| T2+ | 1.52 | 7.23 | 4 |
| HO• | 5.3 | 6.81 | 7.18 |
| DO• | 3.86 | 5.15 | 5.35 |
| TO• | 3.24 | 4.48 | 4.55 |
| HO2• | 9.18 | 10.57 | - |
| DO2• | 7.21 | 8.47 | - |
| TO2• | 6.38 | 7.56 | - |
| O2− | 1.89 | 1.71 | 1.99 |
| Isotopic Pair | Free | Compressed in S State | Compressed in T State |
|---|---|---|---|
| H2+ vs. D2+ | 3.2 | - | - |
| H2+ @C59N vs. D2+ @C59N | - | 101.2 | 104.6 |
| HO• vs. DO• | 11 | - | - |
| HO• @C59N vs. DO• @C59N | - | 15.9 | 21.1 |
| HO2• vs. DO2• | 26.7 | - | - |
| HO2• @C59N vs. DO2• @C59N | - | 33.1 | - |
| Isotopic Pair | Free | Compressed in S State | Compressed in T State |
|---|---|---|---|
| H2+ vs. T2+ | 6.4 | - | - |
| H2+@C59N vs. T2+ @C59N | - | 772.8 | 826.1 |
| HO• vs. TO• | 31 | - | - |
| HO•@C59N vs. TO• @C59N | - | 48.6 | 80.1 |
| HO2• vs. TO2• | 106.3 | - | - |
| HO2•@C59N vs. TO2• @C59N | - | 150.9 | - |
| Molecules | a (H) | a (17O) |
|---|---|---|
| HO• | −23.8 * | −38.8 |
| HO•@C59N triplet | −9.7 | −15.6 |
| O2− | - | −25.0 |
| O2−@C59N triplet | - | −23.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barashkova, I.; Breslavskaya, N.; Wasserman, L.; Buchachenko, A. Isotope and Spin Effects Induced by Compression of Paramagnetic Molecules. Physchem 2022, 2, 253-260. https://doi.org/10.3390/physchem2030018
Barashkova I, Breslavskaya N, Wasserman L, Buchachenko A. Isotope and Spin Effects Induced by Compression of Paramagnetic Molecules. Physchem. 2022; 2(3):253-260. https://doi.org/10.3390/physchem2030018
Chicago/Turabian StyleBarashkova, Irene, Natalia Breslavskaya, Luybov Wasserman, and Anatoly Buchachenko. 2022. "Isotope and Spin Effects Induced by Compression of Paramagnetic Molecules" Physchem 2, no. 3: 253-260. https://doi.org/10.3390/physchem2030018
APA StyleBarashkova, I., Breslavskaya, N., Wasserman, L., & Buchachenko, A. (2022). Isotope and Spin Effects Induced by Compression of Paramagnetic Molecules. Physchem, 2(3), 253-260. https://doi.org/10.3390/physchem2030018





